基于密度峰值剪枝后的最短路径聚类算法

胡恩祥，汪春雨，潘美芹

1.上海外国语大学国际工商管理学院，上海201600

2.华东师范大学计算机科学与技术学院，上海200062

最早在1996年由Ester等[1]提出的DBSCAN 算法使人们意识到密度这一概念的引入，不仅能够直观地解释类别是如何分配的，而且对较大体量的数据和噪声点的数量也有较好的包容性.聚类的速度和准确性得到了明显的提升和改进.此后，围绕DBSCAN 算法的领域半径Eps 值和MinPts 最小点数量展开了讨论，如荆继武等[2]提出的SA-DBSCAN 仍取MinPts=4，但采用了Inverse Gaussian 拟合曲线模拟第4 近邻距离下点概率分布图，用更准确的统计模型计算出实际拐点对应的Eps 值.曹晶等[3]提出了PDBSAN 并认为DBSCAN 采用全局参数，而对不同类型和密度的类别需要分开确定局部参数.通过数据特性进行分区，确定局部参数，局部聚类后再进行局部类合并.基于分区的思想，曹晶等[4]又提出了FDBSCAN，通过选择每一个核心点区域的代表对象，减少区域内的点被重复遍历的次数和可能.后来，Rodriguez等[5]在密度属性的基础上又定义了一个新的距离属性δ，由此提出了CDP 算法，具有较大的密度值和δ值的点作为聚类中心，然后依次对剩余点进行分类.与DBSCAN 算法相比，该算法的核心是通过引入属性δ值使聚类中心表现出更“离群”和突出的特性，同时δ值计算过程也暗示了剩余点的分配规则.这样的CDP 算法通过巧妙的双重属性设置，解决了DBSCAN 算法中通过单一全局密度值判断所有潜在核心点的尴尬情景.2019年，Pizzagalli等[6]在剩余点的分配规则上提出了新的想法，认为剩余点的分配规则应该是基于全局最优而不是局部最优原则，在对一些特殊的链状数据集聚类时CDP 聚类精度出现较大偏差.因此，提出了基于密度峰值的可训练最短路径算法[6]，通过最短路径法从全局出发找到剩余点到真正聚类中心的最佳路径.但该算法在每次最短路径计算过程中都需要遍历全局中所有的路径节点，其中包括对某些不会影响最终计算结果的路径反复迭代，降低了算法运行效率.本文基于Pizzagalli等[6]提出的算法，在最短路径算法的执行上基于对路径图的预先评估，通过截断阈值的设定对一些不会影响最终计算结果的远距离路径进行剪枝，使这些路径不会出现在每一次迭代计算中，从而减少最短路径算法的迭代和运算次数，提升了算法运算效率，进而改进了算法.

1 国内外研究现状

CDP 算法中密度峰值点之间的距离应大于任意一点与比它密度大的点的距离，否则不同密度的类别将无法区分.针对CDP 算法中局部密度的定义问题和剩余点分配问题，国内外学者展开了研究和讨论.Wang等[7]认为基于截断距离dc的局部密度的定义难以确定参数最优解，而提出了基于非线性多元核估计方程来估计局部密度，并通过最大化平均轮廓系数自动选择聚类中心[7].谢娟英等[8]利用K近邻信息定义样本点的局部密度以此反映样本的真实分布信息，提出了基于K近邻的剩余点样本分配策略.Wang等[9]将每一个数据对象作为物理对象来扩散其对给定任务的数据贡献，由此产生数据字段，进而利用数据字段中的熵的不确定性自动提取出最优的截断距离dc，避免了经验估计对于阈值判断的偏误.在面对类簇间样本密度差异较大的情况下，CDP 算法容易忽视密度较小的类簇并将其当作噪声点来处理，高诗莹等[10]将密度比例引入到CDP 算法中，通过计算密度峰值比来提高密度较小类簇的相对重要性和辨识度.当一个类簇中出现多个密度峰值时，CDP 算法无法准确判定聚类中心[10].Zhang等[11]受到层次聚类（hierarchical clustering）算法启发，针对这类具有多个密度峰值的簇聚类问题，首先利用CDP 算法生成原始簇，然后根据集群间的相对互连性和近似性合并子簇.蒋礼青等[12]则受到DBSACN 算法中近邻距离曲线的启发，利用近邻距离曲线中Υ值的第一次跳跃点来判断聚类中心并确定其对应的截断距离dc，利用截断距离dc来指导类的合并及优化.Tang等[13]针对基于聚类的无监督波段选择（unsupervised band selection,UBS）方法，认为当需要多个聚类中心时，CDP 算法的局部密度ρ和距离δ没有适当的缩放方式，提出了先将局部密度ρ和距离δ归一化，重新定义Υ函数，并引入了一个指数化的启发规则调整截断距离dc来提高局部密度ρ的分辨力.此外，CDP 算法剩余点的分配规则强调局部最优准测，即剩余点只关心周围比自己密度更大的点，而不考虑与其他点，尤其是与聚类中心的关联性.Tenenbaum等[14]认为传统的欧氏距离无法检测出数据点间内在的二维属性，提出了利用测地路径进行非线性降维的等距特征映射算法（isometric feature mapping,ISOMAP）.对于非线性流体集上的任意两个点，基于低维流形体利用最短路径法计算测地距离（geodesic distance,GD），即计算在三维空间中曲面上A和B两点间的最短距离以此生成一个全局最优的关联规则.Xu等[15]提出了一种流形密度峰值聚类（manifold density peaks clustering,MDP）算法，该算法基于测地距离计算距离矩阵，根据聚类数目自动识别出聚类中心并通过ISOMAP 算法实现对高维数据集的降维处理.Du等[16]认为在诸如折叠、扭曲、弯曲的流形体数据集上CDP 算法不能够有效地聚类，进而提出了基于测地距离来确定密度峰值的算法.通过重新计算各点之间的测地距离，缩短了处在同一类簇中点与点间的距离，放大了处在不同类簇中的点与点间的距离，密度峰值点的距离δ值将会显著增加，从而在决策图上能够更准确找到密度峰值.本文所介绍的TP-CDP 算法以及在此基础上提出的PTP-CDP 算法，都是利用截断距离dc定义局部密度确定聚类中心，在剩余点的分配规则上则是通过评估各点之间路径的属性从全局角度寻找最优解.

2 基于密度峰值剪枝后的最短路径聚类算法

2.1 CDP 算法

CDP 算法[5]假设聚类中心周围都是密度比其低的点，且与其他密度较高的聚类中心之间距离更远，以此形成不同的类别.算法定义密度ρi为点i在给定截断距离dc内点的数目，该算法只对不同点密度的相对重要性敏感.对大数据集来说，其稳健性与截断距离dc的选择相关，即

在定义密度属性后，CDP 算法又定义距离δi为所有密度比i点大的点与i点距离的最小值，即

通常定义密度最大的点与其他点距离的最大值为δi.在CDP 中通过较大的密度ρi和距离δi值确定聚类中心和离群点的情况.具体选择聚类中心的数目则通过定义Υi计算出每个点的对应值，按照降序排序在图像中选择突变点对应于聚类中心的数量，其中

在剩余点的分配问题上，通过CDP 算法，在确定聚类中心后剩余的点按密度降序依次被分配到离该点最近、密度更高的点所属的类中.剩余点的分配规则与δi定义存在联系，在计算每个点的距离δi时通过寻找距离自己最近且密度比自己大的点，以此形成了某种类的“关联”，即这两个点相互绑定，归属于同一类中.从聚类中心开始向外进行类扩充，遵循密度降序，通过距离δi的穿针引线，每一个点都在局部达成了最优的分配结果.

2.2 基于密度峰值的可训练最短路径算法

基于密度峰值的可训练最短路径算法（TP-CDP）[6]针对CDP 算法中剩余点的分配规则提出了质疑，认为剩余点的分配应该基于全局最优而不是局部最优.在CDP 算法剩余点的分配过程中，剩余点被分配到最近且密度比自己大的点所属的类中.其中，如果有密度较大的点分类错误，则会导致其附近密度比它小的点也随之分类错误.该算法基于两种链状数据和环状数据集，证实了CDP 算法中剩余点可能的分配错误.在该类数据集中，造成CDP 算法聚类错误的原因主要是某些其他类别离自己应真正所属的链状、环状类间距离太近，导致聚类错误.图1列举了CDP 在具有上述数据分布特征的集上错误的聚类结果.

图1 CDP 在3 种数据集上聚类结果Figure 1 CDP clustered in three different datasets

图1中，3 种不同的数据集基于CDP 算法聚类出现明显错误的原因相同，这里我们选择分析图1(c)的聚类结果来清楚地解释CDP 算法聚类发生错误的原因.

如图2所示，在剩余点的分配过程中出现了某个密度稍大的剩余点3，然而比点3 密度更大点只有作为聚类中心的点1 和2，点3 到达聚类中心点2 的欧氏距离小于到达聚类中心点1 的欧氏距离.此时根据CDP 剩余点的分配规则，点3 选择归属于比自己密度更大且距离更近的点所属的类中，也就是聚类中心点2 所属的类.由此出现了局部聚类错误，而这又会导致点3 周围密度比自己小，且距离自己较近的其他剩余点也同点3 一样聚类错误.

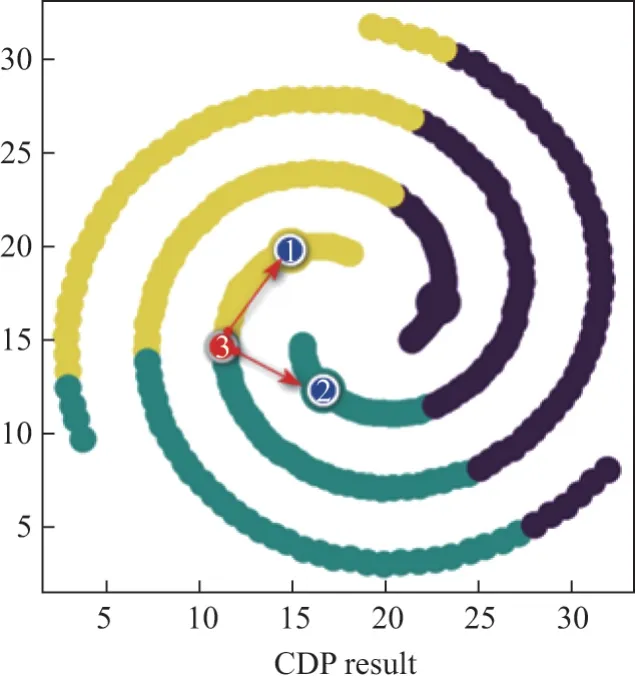
图2 CDP 剩余点分配错误示意图Figure 2 Remaining points incorrectly allocated by CDP

针对剩余点的分配问题，TP-CDP 算法提出一种全局最优规则，认为剩余点的分配应该基于最短路径法，从不同的聚类中心出发选择到达该点最短距离的路径，由此确定剩余点所归属的聚类中心.算法先假定空间中存在一个虚拟节点s连接到每一个聚类中心的距离设置为0，目标是找到以s点为源的所有点的单源最短路径，对应以s点为根的最小生成树.定义加权后的路径成本函数，即

当P≥1 时，路径成本函数ξp(Γ)惩罚高成本即距离较大的边.随着p值的增大，拥有较大距离的路径在路径成本函数的计算中将占据更大的权重，当p值趋向正无穷时，路径成本函数的计算结果将近似于单条路径中的距离最大值.TP-CDP 算法认为有必要惩罚距离较大的路径，通过赋予这些路径更大的权重使较大路径无法再“走通”.理由是，宁可选择更多的小路径拼接起来，绝对距离可能较长的线路，而不愿选择在绝对距离可能较小，但包含了较大距离的路径线路，避免因为链状类数据围绕的干扰而产生的局部聚类错误.由于单源最短路径算法每一次运算都要遍历所有的点计算加权后的最短距离，因此算法平均时间复杂度为O(n2).

2.3 基于密度峰值剪枝后的最短路径聚类算法

本文基于密度峰值的可训练最短路径算法，提出一种基于密度峰值剪枝后的最短路径聚类算法（PTP-CDP），认为在路径计算迭代之前设置一个截断阈值，而这个截断阈值就是CDP 算法中初始不断测试的领域半径值，即截断距离dc.因为在加权路径成本计算过程中，某些较大成本的边永远不需要出现在某次计算或某条路径中.通过最初对每一条边的计算，先剪切掉路径图中大于截断阈值dc的边，使成本较大的边永远不会出现在后续的迭代计算中，然后得到的单源最短路径也不会包含较大路径，符合我们的要求和预想.由此我们得到PTP-CDP 算法的平均时间复杂度为O(n2)，与TP-CDP 一致.但在面对大数据集时，PTPCDP 在求单源最短路径的环节中对图的剪枝后，通过priority_queue 实现的Dijkstra 最短路，堆中元素O(|V|)个，在每次更新时往堆里插入当前最短距离和顶点的值O(|E|)次，所以PTP-CDP 的最短路部分平均时间复杂度为O(|E|ln|V|)，而TP-CDP 的最短路部分没有剪枝，相当于是通过邻接矩阵实现，认为每两个顶点之间均有边连接，所以TP-CDP 的平均时间复杂度为O(|V|2).因此，本文算法在样本点越多、类间距离越大的情况下，比TP-CDP 算法的性能更具优势.通过反复实验测试和对比，也证实了截断距离dc的设置能够减少算法的运行和迭代次数，提升算法的运行效率并改进原有算法.

3 对比实验

本文在测试对比CDP、TP-CDP、PTP-CDP 算法之前，首先对原有CDP 算法中的一些细节进行了改进.在样本密度ρi的定义下，当数据点连续时原CDP 算法中的局部密度定义并不能很好地反映数据点密度的连续性，因此我们采用指数核[17]来计算局部密度，计算公式如下：

式(6)不仅表示了局部点密度的连续化，而且对计算规模较小的数据集来说，在给定截断距离dc内的局部点密度，可以使不同点局部密度特征更加紧凑，表现更好.在判断聚类中心的数目时，采用Kneed 拐点检测曲线[18]自动判别Υi −i决策曲线图上的拐点，实现了聚类中心数目的自动化确定.整个PTP-CDP 算法的伪代码如下：

事实上，本文所提出的PTP-CDP 算法与TP-CDP 算法本质上并无差别，只是在单源最短路径中采用截断距离时，省去了一些不会影响最终计算结果的远距离路径.Pizzagalli等[6]根据Wiwie等[19]研究的生物聚类指标性能比较选择F1-score 和Jaccard Index 评估指标，证实了TP-CDP 算法聚类精度相比于CDP 算法是有效提升的.本文选择外部聚类指标Jaccard Index 和Rand Index[20]来证明在聚类精度上PTP-CDP 与TP-CDP 基本保持一致，在算法效率提升的问题上是本文的重点.图3为基于PTP-CDP 算法对前文提及的几个链状、环状数据集再聚类的结果图.

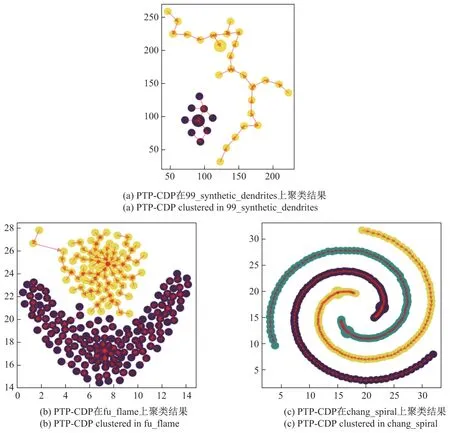
图3 PTP-CDP 在3 种数据集上聚类结果Figure 3 PTP-CDP clustered in three different datasets

无论是TP-CDP 或是本文提出的PTP-CDP 算法，其聚类中心的确定方法都与CDP 算法一致，只是在剩余点的分配规则中TP-CDP 基于全局最优准则确定点所归属的类，PTPCDP 则是在计算每个点的全局最短路径时利用Eps 作为截断阈值，减少不必要的路径计算和迭代次数.因此，我们首先对含有类标签的数据集进行外部指标的聚类精度测试，证明本文PTP-CDP 并没有从本质上影响TP-CDP 聚类的精度.接下来对14个数据集进行测试，这些数据集中包含有链状、环状类数据的特征，大部分由ClustEval 数据平台、UCI 机械学习数据库提供，有些则是人工合成数据集.本文数据集的测试量级大部分在3 万∼5 万区间内，实验测试环境基于Intel(R) Core(TM) i7-5500UCPU @2.4 GHz.

图4表示外部聚类精度指标Jaccard Index和Rand Index 在不同数据集上的基于3 种算法的精度差异.

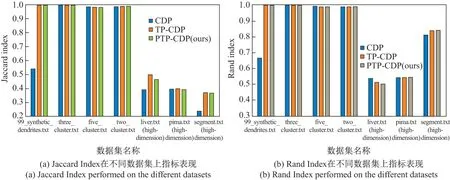
图4 外部聚类精度指标在不同数据集上的表现Figure 4 External clustering accuracy index performed on the different datasets

外部聚类精度指标Jaccard Index 和Rand Index 在[0,1]区间内，指标数值越接近1，聚类越精确.图4表示PTP-CDP 和TP-CDP 在大部分数据集上精度保持一致，PTP-CDP 在少数数据集上精度的损失并不显著，在可接受的误差范围内.在99_synthetic_dendrites、three_cluster 等人工合成的无噪声点的数据集中，TP-CDP 和PTP-CDP 都近乎实现了完全正确聚类，聚类精度指标接近1 且彼此没有差异.而对liver、pima 等高维数据集，TP-CDP 和PTPCDP 虽然聚类精度有所下降，但都在0.5 以上.PTP-CDP 相比TP-CDP 在大部分数据集上精度保持不变，在极少数据集上有些精度损失，但精度损失在1%左右.考虑到路径剪枝对路径计算迭代的显著减少，少量精度损失完全在误差允许的可接受范围内.表1显示了各数据集的规模、测试次数、参数Eps、p值及3 种算法的测试时间均值的信息.

通过本文PTP-CDP 算法测试结果不难看出，在各个类型数据集上相比TP-CDP 在执行时间（单位s）均有不同程度的提升.其中，p值表示路径成本函数ξp(Γ)对较大路径的惩罚程度，p值越大则拥有较大距离值的路径在路径成本函数的计算中权重也越大.在本文的数据测试中，取p=2 已经满足了算法的需求.图5显示了在不同数据集上PTP-CDP 相较于TP-CDP 算法时间的提升比例，我们在相同的计算机运行状态下测试每一个数据集的CDP、TP-CDP 和PTP-CDP 运算时间，重复10 次取时间均值，经计算PTP-CDP 算法速度的时间均值提升了2.147 8%.

通过对不同类型数据集的测试可以看出，在与TP-CDP 算法聚类精度保持一致的前提下，PTP-CDP 在具有显著的链状类、环状类数据特征的数据集中速度提升较大，而在普通的类别数据中表现一般，这也与我们算法的思想一致.在具有更大数据量的链状数据集中，当Eps 值越小时，从剩余点出发时可以截断更多显著不需要的路径，减少路径成本函数的计算和迭代步骤，算法的速度也会得到显著提升.同时，在人脸面部识别等高维数据集中，传统的聚类算法针对高纬度数据的低性能，PTP-CDP 在此方面也有不错的表现.

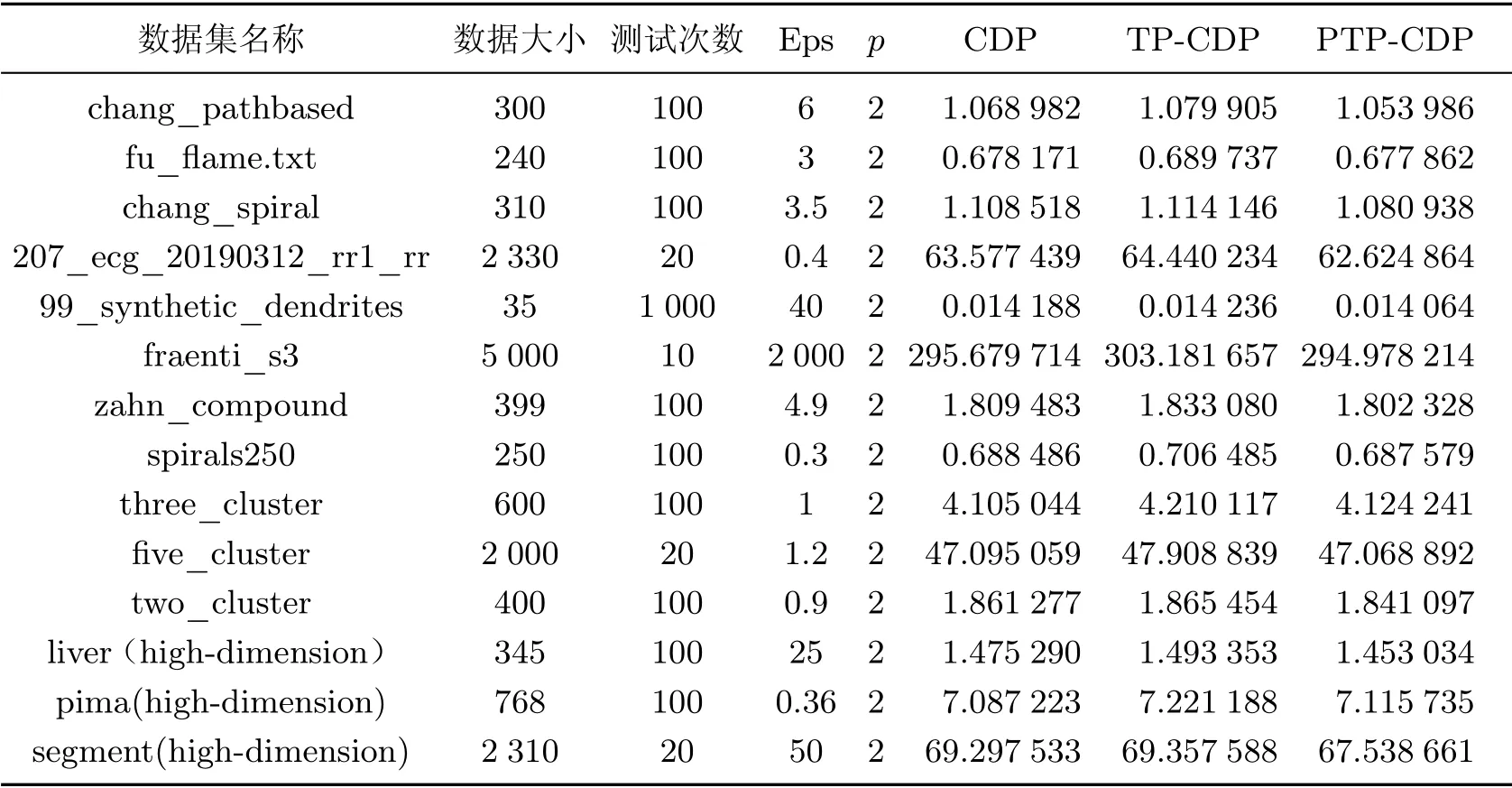
表1 数据集信息及测试时间均值Table 1 Information of datasets and the average of the testing time s

4 结 语

本文从基于密度的DBSCAN 算法入手，着重分析了CDP 算法的聚类机理，并介绍了为解决CDP 算法在链状、环状类上聚类不准确问题而提出的TP-CDP 算法.通过分析TP-CDP 算法在剩余点分配问题上所采用的最短路径算法，提出了将超参数Eps 值作为截断阈值dc，减少了不需要的路径成本计算和最短路径法的迭代次数，并通过实际测试数据集证实了我们的假设.在保持聚类精度不变的前提下，减少了TP-CDP 算法的计算时间，改进了算法.实际上，在全局完全图中求解最短路径时，在聚类中应遵循类内距离尽可能小、类间距离尽可能大的准则.截断阈值dc就是让最短路求解过程尽可能在类内中展开，而剪去属于类间距离的较大路径，这是因为这部分路径成本经过加权后对求解最优的最短路径并无帮助.

本文借鉴了TP-CDP 算法，该算法基于最短路径法对剩余点进行全局分配，针对这种全局分配规则提出改进算法PTP-CDP.未来TP-CDP 算法改进的可能，会侧重于剩余点的分配过程中采用怎样的全局最优的分配准则可以得出唯一最优解，以此确定剩余点的类归属问题.此外，本文在截断距离dc的设置上采用超参数Eps 值，是否有其他更好的截断阈值，在满足聚类精度的前提下，还能进一步减少不必要的计算过程和迭代次数，这方面值得我们去探究.另外，在剩余点的分配问题上，除了基于最短路径算法的分配规则，是否还有其他高效可行的方法既能够勾画出样本的整体空间分布规律，又能够有效地找到全局计算中的最优解，值得我们在未来不断去探寻和发现.