毛竹与桉树蒸散估算公式修正及对比分析

王眉樾, 张兰珍, 翟禄新, 刘芸瑜, 黎 婵, 欧晓华, 廖伟婷, 迟晋浙

(广西师范大学 环境与资源学院, 广西 桂林 541004)

蒸散量是生态系统水分循环与水量平衡的重要组成部分，准确测定与计算蒸散量对水资源评价与水资源的高效利用具有重要意义[1]。目前，计算蒸散量的主要方法有实际测量法和公式估算法，实际测量法在操作过程中要耗费大量的人力和时间，因而基于参考蒸散公式来估算实际蒸散量(ETa)成为更加便捷的选择。在国际上，常用来计算参考蒸散量(ET0)的公式很多，这些公式可大致分为半经验法、气象相关法、辐射相关法、空气动力学法、综合法等几类[2]。由于不同区域影响ET0的主导因子不同，某些基于部分气象参数的公式虽然在某些特定条件下能够较好地估算ET0，但是在其他地区应用时误差却较大[3]，故有必要进行修正，以准确估算ETa。此外，不同的公式提出时估算的时间尺度也不同，有些公式估算的是月蒸散量，有些则是用于估算日蒸散量。因此，在实测蒸散量的基础上，对参考蒸散公式进行修正，并在修正过程中以修正系数来综合体现当地作物系数和尺度转换，不失为一种行之有效的方法。

在中国南方地区，良好的水热资源为毛竹和桉树等人工林发展提供了优越条件，但也引发了关于水分消耗过大的诸多争议[4]。国内针对人工林的植被水分效应研究较多，多集中于毛竹或桉树种植对土壤性质、土壤水分和地表径流的影响[5]。有研究显示，毛竹林的径流量较大，水分利用效率较低。饱和水汽压差和环境温度对毛竹林水分利用效率有显著影响[6]，毛竹蒸腾速率与净光合速率极显著相关，与生长时期极显著相关，而与竹龄的相关性则不显著；水分利用效率总体表现为日尺度变化，快速生长中期显著高于前期和后期，5 a生毛竹高于3 a生毛竹[7]；桉树的树干液流日动态变化呈中午高、早晚低的单峰型变化；与杉树相比，桉树的单木日均耗水量大于杉木的日均耗水量；桉树对水分的获取能力大于杉木[8]。在蒸腾耗水方面，有研究表明桉树的树杆液流与饱和水汽压差和太阳辐射有极显著的相关性，桉树年蒸散量占年降水量的70%左右[9]。上述研究均基于茎流观测或土壤水分观测，属较微观的研究尺度。中尺度的研究则较多选择依据现有参考蒸散估算公式，经修正后进行实际水分消耗的估算[10-13]，但不针对某一特定的植被种类。

本文以广西桂林市雁山区为研究地点，以盆栽毛竹[(Phyllostachysedulis)，本研究以青竹(Phyllostachysflexuosa)代替进行试验)]和巨尾桉(Eucalyptusgrandis×E.urophylla)为参考作物，以称重法测量所得的逐日ETa为参考标准，选用应用较为广泛的FAO Penman-Monteith，Hargreaves1975，Hargreaves1985，Turc，Priestley-Taylor，Makkink，Doorenbos-Pruitt，Abtew，Jensen-Haise 9个估算公式计算逐日ET0，并探讨不同公式的适用性。针对计算误差较大的公式，分析ETa与ET0的相关性，对不同公式通过线性回归进行修正，使其更适用于计算桂林市雁山区毛竹和桉树的实际蒸散量，为当地的人工林水分管理及预测提供参考依据。研究结果也有助于探索当地特有植物蒸散的影响因素，理解蒸散过程的机制，探寻不同植被的水分行为差异，认识人工林对生态系统的影响。

1 试验材料与方法

1.1 试验材料

选用规格相同的8个桶口内径30 cm、桶底内径25.5 cm、桶内高30 cm的塑料桶，在其下方固定位置安装排水装置，选取长势相同的3丛毛竹和5棵巨尾桉栽于花盆中。毛竹以花市购买的青竹代替，每盆栽植4～5株，单株基部直径1.0～1.2 cm，试验期间平均高190～230 cm，冠幅40 cm×60 cm。巨尾桉为去杆移栽的树桩，树桩高度为30～40 cm，基部直径为4～6 cm。移栽树桩上新生萌枝30 d后开始试验观测，试验期间萌枝平均基部直径为0.5～1 cm，整株桉树高80～120 cm，冠幅60 cm×100 cm。

1.2 蒸散发量的计算与测定

1.2.1 参考蒸散发量 本研究以位于广西桂林市雁山区的自动气象站(气象站型号为FR210，北京澳作制造)2018年8月1日—2019年2月25日的逐日气象要素观测值作为数据源，运用9个公式(表1)估算ET0。气象要素包括平均气温、平均湿度、平均气压、平均风速、降水量和日照时数等(图1)。

1.2.2 实际蒸散发量 用HZ-TCS电子秤(精度为0.001 kg)于每日固定时段18：00—19：00测量花盆质量，为减小质量测量误差，测量前把盆栽周围的枯枝落叶捡回盆内，且对各个样本进行两次称量，取其平均值。为了确保样本正常生长，在干旱时期对样本进行灌水、降雨后进行排水，并记录灌水量(kg)和排水量(kg)。在考虑降水量、灌溉水量的前提下，两日的盆栽质量差换算为水深即为作物的ETa(mm)。

1.3 研究方法

以实际测量的ETa作为标准值，采用FAO Penman-Monteith，Hargreaves1975，Hargreaves1985，Turc，Priestley-Taylor，Makkink，Doorenbos-Pruitt，Abtew，Jensen-Haise法计算作物的ET0。各方法的公式表达及参考文献见表1，各式中符号说明详见参考文献。利用线性回归方法和均方根误差(RMSE，Root Mean Square Error)，分析比较ETa和9个公式估算的ET0的差异。

表1 毛竹和桉树蒸散发量估算公式

修正公式为：

Y=mX+n

(1)

式中：Y为实测值，即ETa；X为以参考蒸散公式计算的ET0；m和n分别为斜率和截距。

以决定系数(R2)和均方根误差(RMSE)为评价的指标，评价9个公式估算的ET0与实际测量值的差异。对于修正前后实际蒸散量与估计蒸散量的差异，用均方根误差(RMSE)表示：

(2)

最后，用Taylor图来展示修正前后的相关参数的变化。

2 结果与分析

2.1 毛竹蒸散估算公式修正

利用未修正的9种方法估算的雁山区盆栽毛竹的ETa与ET0的关系如图2所示。总体上，9种公式估算的ET0与实测ETa的线性相关性良好，决定系数R2为0.576～0.723，ET0与ETa变化趋势一致，说明模型结构合理，可通过修正参数来提高精度。各估算公式计算的散点趋势线与1∶1线仍有不同程度的偏离，除FAO Penman-Monteith法外，其他方法均存在低估的特点，且随着蒸发力越高，低估的程度越大，其中Abtew法最明显。FAO Penman-Monteith法计算的ET0在实测ETa上下波动，存在低蒸发力下低估、高蒸发力下高估的阈值特点，其临界值为3.92 mm/d，即在大气强蒸发力的气象条件下使用该模型将产生较大误差。Hargreaves1975法与实测值吻合度最好，决定系数达到0.723，为9个模型中最高值。

图1 研究时段气象要素

图2 修正前9种方法计算的ET0与毛竹实测ETa的关系

图3为修正后的ETa与ET0的散点图。将实测值ETa与9种方法计算的日ET0的均方根误差列于表2。修正后，9种方法与实测蒸散值具有良好的线性关系，修正后RMSE较修正前减小幅度最明显的是Turc法，从修正前3.513变为修正后1.294；其次是Makkink法，从修正前2.577变为修正后1.294。修正后Hargreaves1975的RMSE最小，其次是Jensen-Haise法，计算结果与实测值最为接近，能较好地模拟实际蒸散发。

为说明修正前后标准差和中心化的均方根误差(CRMSE，Centered Root Mean Square Error)的变化，以Taylor图来说明两参数的变化，见图4。修正前，Jensen-Haise，Hargreaves1975，Doorenbos-Pruitt这3种方法标准差和中心化的均方根误差均与实测值比较接近，即代表性较好。经过修正，标准差趋近于观测值的标准差(图中的REF)，除Hargreaves1975和Jensen-Haise法外，其他方法的中心化均方根误差均显著下降。

2.2 桉树蒸散估算公式修正

由图5可以看出，总体上，修正前9种公式法估算的ET0与实测ETa的线性相关性良好，决定系数R2为0.671～0.794，9种方法计算的ET0与ETa变化趋势一致，各算法的散点趋势线与1∶1线仍有不同程度的偏离。9种方法均存在低估的特点，且随着蒸发力越高，低估的程度越大，其中Abtew法偏离最明显。FAO Penman-Monteith法计算的ET0在实测ETa的上下波动，存在低蒸发力下低估、高蒸发力下高估的阈值特点，临界值为9.72 mm/d。修正前FAO Penman-Monteith法与实测值总体吻合度最好，但决定系数仅为0.671。

桉树蒸散发量估算公式修正后的散点图如图6所示。将实测值与9种方法计算的日ET0的均方根误差列于表3。修正后，9种方法中RMSE较修正前减小幅度最明显的是Turc法，从修正前5.194变为修正后1.416；其次是Makkink法，从修正前4.159变为修正后1.460。在各种方法中，修正后Jensen-Haise的RMSE最小，其次是Hargreaves1985，计算结果与实测值最为接近，能较好地模拟实际蒸散发。此外，修正前FAO Penman-Monteith，Hargreaves1975和Jensen-Haise法估算结果较好。

图3 修正后9种方法计算的ET0与实测毛竹ETa的关系

表2 估算的ET0与称重法实测毛竹蒸散值均方根误差(RMSE)

同样，以Taylor图来说明修正前后桉树的估算蒸散量与实测蒸散量的标准差和中心化的均方根误差的变化，见图7。结果与毛竹蒸散情况一样，修正可以使桉树蒸散量的标准差和中心化均方根误差更趋近于观测值的相应参数。值得注意的是，从图4和图7对比可以看出，对于标准差而言，修正后桉树蒸散量的标准差大于毛竹的标准差。对于中心化均方根误差而言，修正前桉树蒸散量的中心化均方根误差大于毛竹的中心化均方根误差，修正后两值接近。

2.3 两种植物的蒸散量比较

为说明两种植物的实际蒸散量差异，特列出两种植物蒸散量估算公式的修正系数，见表4。桉树的修正斜率均大于毛竹，即在相同的气象条件下，修正后的9个公式估算的桉树蒸散量均超出毛竹的蒸散量约38.0%，这与实测的两种植物的蒸散量的差异一致。

3 讨 论

3.1 公式修正的适用性

基于最小二乘法的估算公式修正中，多以某一估算标准或实测标准(如FAO Penman-Monteith或蒸发皿蒸发量)为依据，对其他蒸散公式进行研究修正[10,13]，并分析修正系数与区域气候指标的关系[11-12]。这些修正工作在某种程度上揭示了参考蒸散发量计算公式的估算误差与当地气象因子的关系，为众多蒸散估算公式的“本土化”提供了新的思路。本研究是以实测的盆栽植物(毛竹和桉树)蒸散为基准进行估算公式修正，修正系数中隐含着蒸散估算中常用的作物系数(即ETa与ET0的比值)，而作物系数则是当地气象因子的函数。因此，寻求修正系数与气象因子间的关系将是克服作物系数经验性的有效途径。前面的结果分析说明，不同的公式直接用于蒸散估算时，其误差差异较大。通过修正，这些参考蒸散量公式可以应用于不同植被的实际蒸散估算。前述分析表明，有些估算公式修正前具有较好的代表性，即不加修正也可以用于ETa估算，如FAO Penman-Monteith，但更多的公式必须修正后才能用于ETa估算。

注：A为FAO Penman-Monteith，B为Hargreaves1975，C为Hargreaves1985，D为Makkink，E为Turc，F为Priestley-Taylor，G为Jensen-Haise，H Doorenbos-Pruitt，I为Abtew，下图同。

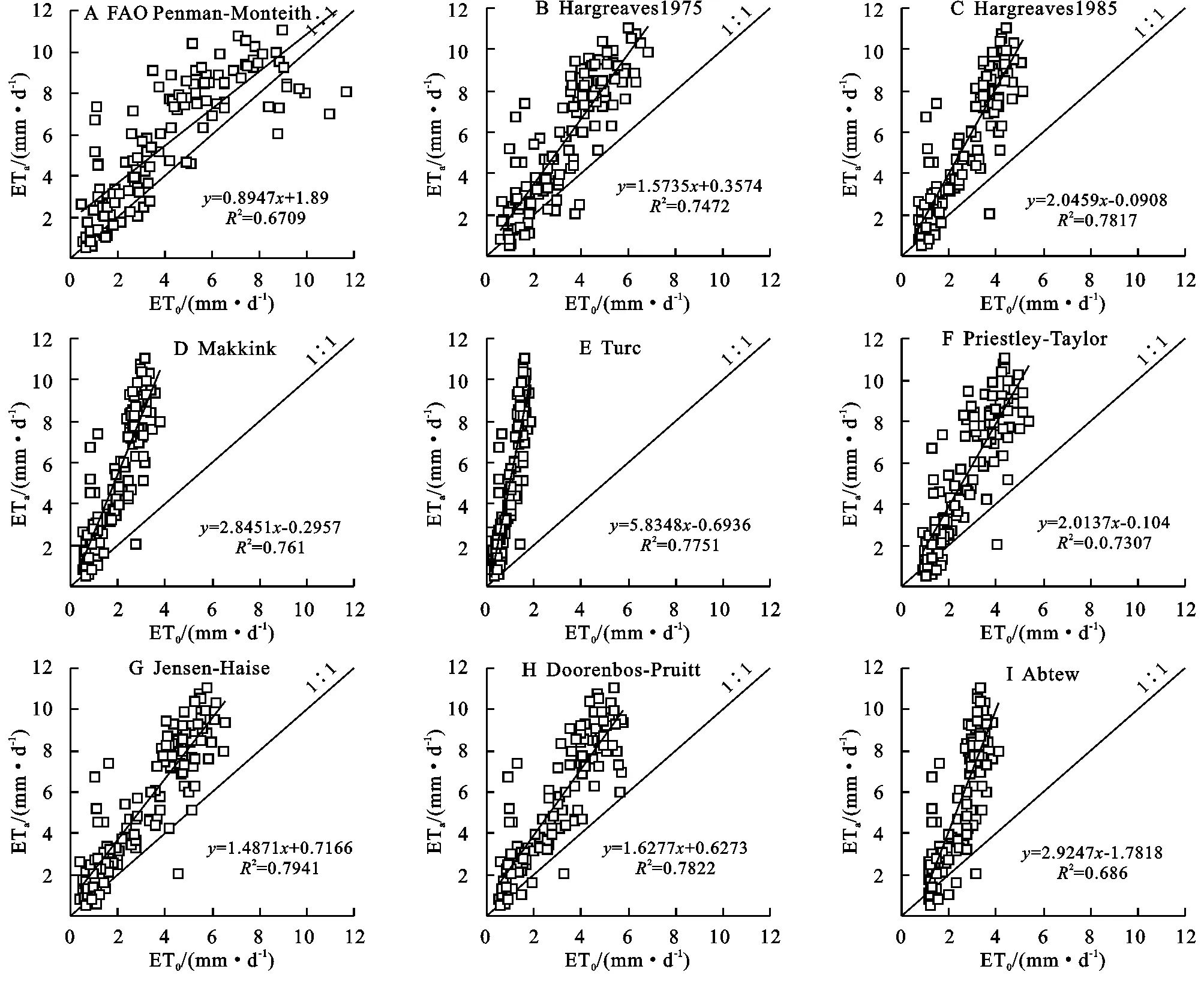
图5 修正前9种方法计算的ET0与实测桉树ETa的关系

3.2 两种植物的蒸散差异

相较于桉树来说，毛竹的蒸散量离散性较小，中心化的均方根误差为2.348，而桉树的则为3.068。即在相同的气象条件下，桉树的蒸散量更加变化剧烈，而毛竹则相对比较稳定。此外，在气象条件相同的情况下，两种植物的修正系数的差别反映了两种植物的蒸散差异，即桉树的蒸散量明显大于毛竹的蒸散量。现有仪器实测和遥感估算的研究结果也表明，桉树的单木日均耗水量大于其他树种(杉木)的日均耗水量，桉树对水分的获取能力较大[8]，桉树林区蒸散发量大于天然混交林区，桉树林的生长过程相对天然混交林将消耗更多的水分，并对该区域的水循环过程产生影响[23]。由此表明，基于估算公式的修正系数，也一定程度上体现了不同植物水分消耗的差异，这为澄清备受争议的桉树水分消耗问题提供证据。

表3 估算的ET0与称重法实测巨尾桉蒸散值均方根误差(RMSE)

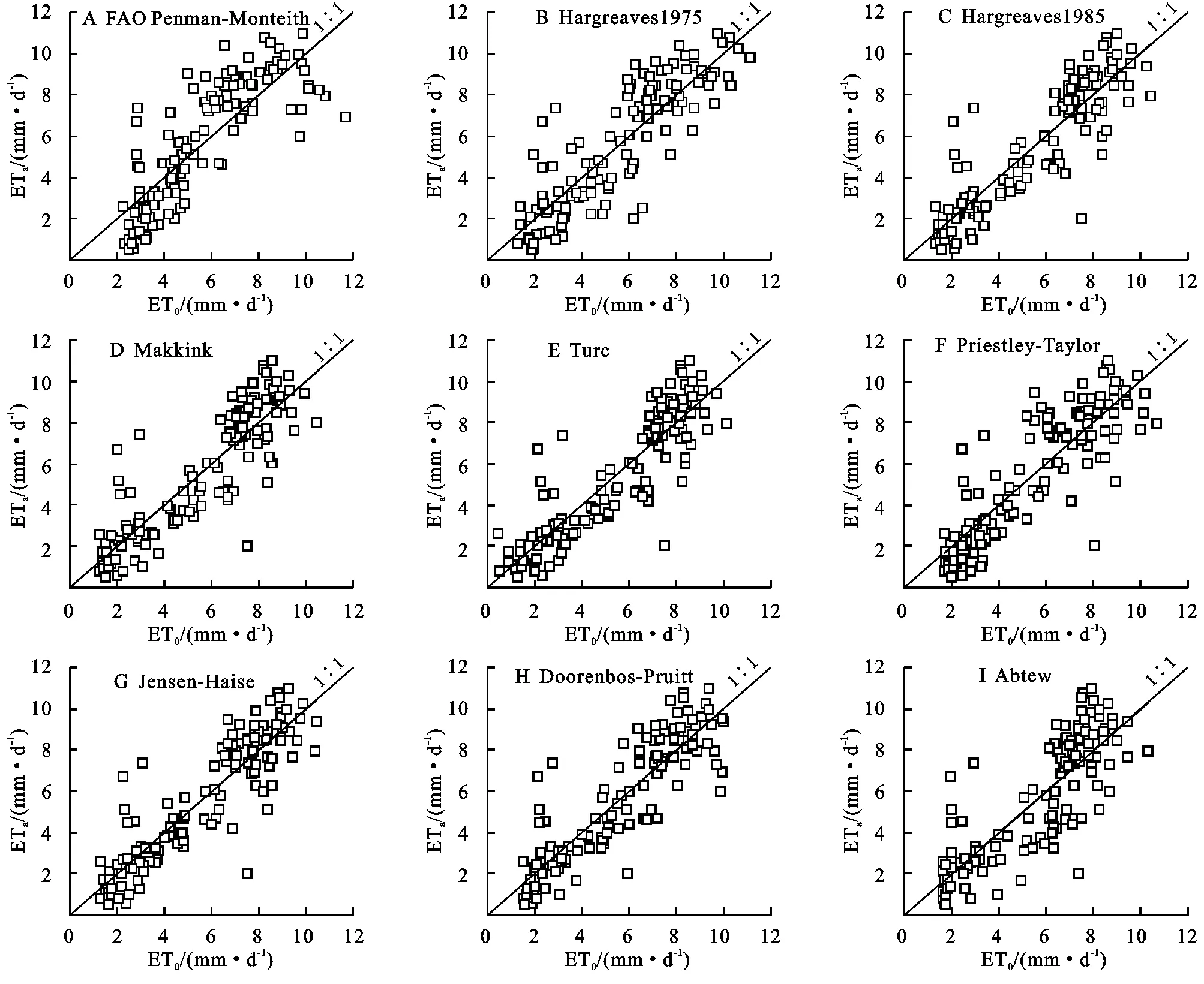
图6 修正后9种方法计算的ET0与实测桉树ETa的关系

3.3 实际蒸散的影响因素及敏感性

公式是经验性的总结，其本质上是蒸发规律的总体反映。FAO Penman-Monteith公式是基于太阳净辐射、土壤热通量(日尺度计算时可取为零)、气温、风速和水汽压差来建立的，即基于空气动力学和能量平衡，故综合性较强，适用性也最好。Hargreaves1975和Jensen-Haise公式是基于平均气温和太阳辐射的估算公式，对毛竹而言此两式修正前计算结果最好，说明在研究区，气温和辐射是决定毛竹蒸散量的关键象因子。但对桉树来说，FAO Penman-Monteith，Hargreaves 1975和Jensen-Haise公式均有较好的表现。说明桉树的蒸散可能更多地取决于除气温和辐射之外的风速及水汽压差。

Doorenbos-Pruitt公式和Makkink公式有近似的表达式，但Doorenbos-Pruitt公式的系数α中包含了相对湿度和风速[21]，故本质上讲，两公式还是有较大的区别，且就估算结果而言Doorenbos-Pruitt公式明显优于Makkink公式。

图7 修正前后桉树蒸散估算结果Taylor图

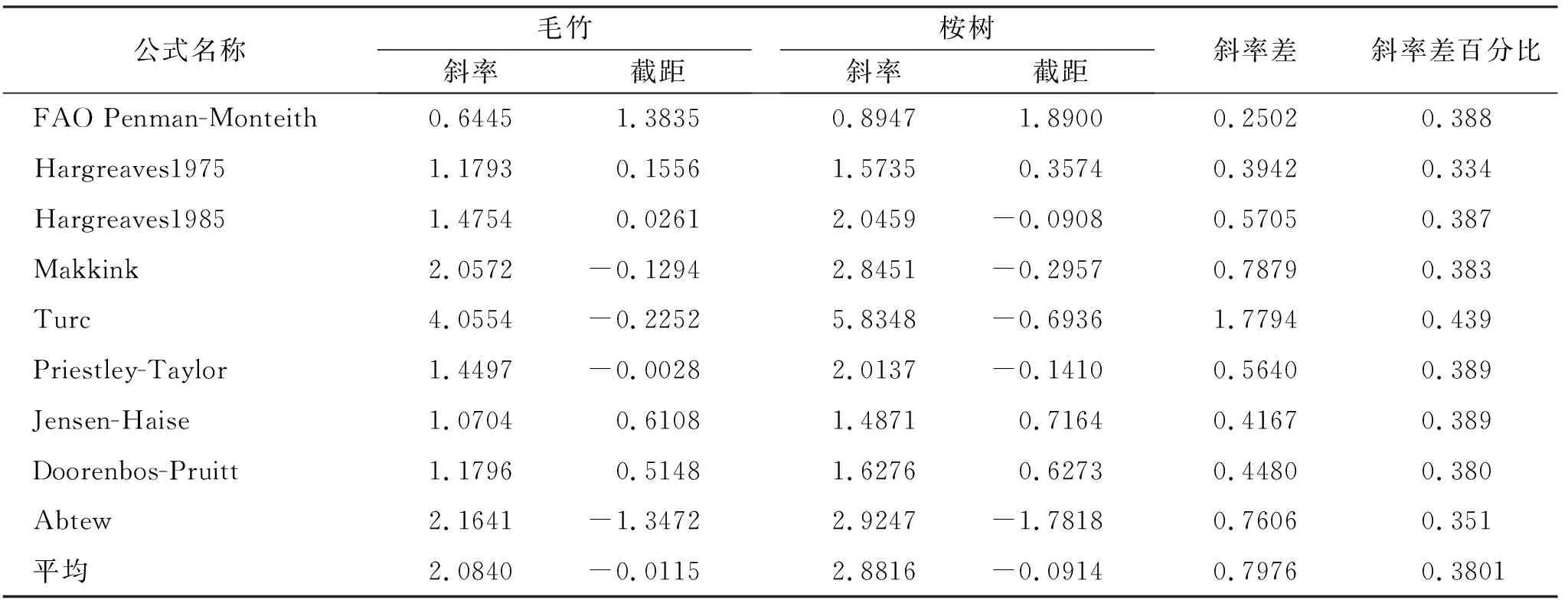
表4 毛竹和桉树估算公式修正系数

根据前述公式(1)，修正系数中的斜率m(表4)相当于ETa对于原始公式估算量(ET0)的导数(∂Y/∂X)，因此修正斜率m可理解为ETa对于某单一气象要素或者多个气象要素组合的敏感系数，即气象要素或气象要素组合的单位变化引起的ETa的变化。在此基础上可以看出，对试验所在区域的两种植物而言，9个公式估算的ETa对气象要素的敏感性从大到小依次为Turc，Abtew，Makkink，Hargreaves1985，Priestley-Taylor，Doorenbos-Pruitt，Hargreaves1975，Jensen-Haise，FAO Penman-Monteith，其在桂北地区的适用性则与此次序相反。对于毛竹和桉树而言，桉树的修正斜率大于毛竹的修正斜率，即桉树的蒸散量对气象要素更加敏感。

4 结 论

(1) 修正前，对于毛竹Jensen-Haise，Hargreaves1975，Doorenbos-Pruitt这3种方法的估算结果较好；对于桉树来说，则是FAO Penman-Monteith，Hargreaves1975和Jensen-Haise法估算结果较好。修正可有效提高估算公式的精度并可在一定程度上揭示两种植物的蒸散对气象因子的敏感性。

(2) 在相同的气象条件下，桉树蒸散量的日变化更加剧烈，而毛竹的蒸散量则相对比较稳定。桉树的蒸散量大于毛竹的蒸散量，即在相同的气象条件下，桉树比毛竹多耗水38.0%左右。

(3) 不同的植物对于不同的气象要素敏感性不同。9个公式估算的ETa对气象要素的敏感性由大到小依次为Turc，Abtew，Makkink，Hargreaves1985，Priestley-Taylor，Doorenbos-Pruitt，Hargreaves1975，Jensen-Haise，FAO Penman-Monteith。敏感性越高的公式本身的适应性越差，即公式本身在桂北地区的适用性依次为FAO Penman-Monteith，Jensen-Haise，Hargreaves1975，Doorenbos-Pruitt，Priestley-Taylor，Hargreaves1985，Makkink，Abtew，Turc，故在应用中更应该注意修正。毛竹和桉树相比较，桉树的蒸散量对气象要素更加敏感。

本研究由于观测时段较短，公式修正中未能体现季节差别。此外，修正系数中隐含着蒸散估算中常用的作物系数，揭示修正系数与当地气象因子的关系，则是未来研究中的值得探索的方向。