基于广义共同邻居的有向网络链路预测方法

赵学磊，季新生，刘树新，赵宇

（信息工程大学，河南 郑州 450001）

1 引言

近年来，复杂网络逐渐成为探究真实复杂系统内在机理的抽象化工具，其重要方向链路预测[1-4]得到了研究人员的持续关注。链路预测旨在利用网络中已知信息预测网络中的未知连接[5]、未来连接[6]或错误连接[7]，是复杂网络与信息科学交叉融合的重要桥梁，对研究网络演化[8-11]、未知链路探测[12]等具有巨大的实际应用价值。

当前，针对无向网络的链路预测研究已取得众多成果，吕琳媛[3-4]详细对比分析了各种方法，并将其归类为局部相似性、全局相似性指标。局部相似性指标优势在于计算复杂度低，适用大规模网络。全局相似性指标考虑全网拓扑信息预测精度更高，但会付出较高计算代价。然而，前期研究集中于无向网络，并且现有局部或全局指标均难以直接应用于有向网络的预测。

局部相似性指标以共同邻居[13]（CN，common neighbor）指标最具代表性，因有向网络中连边具有方向性，使无向共同邻居衍生多种异构形式，传统预测方案忽略不同异构形式之间差异，极大降低了有向网络中的预测精度，甚至使预测失去意义。文献[14]研究发现，有向网络存在特殊的互惠机制，即节点倾向于建立反向的连接以回应其他节点对自己的连接，故有向网络中存在部分双向的链接，称之为互惠边，互惠边在促进连边产生时通常比单向连边发挥更大作用，表示节点间具有更为紧密的局部结构，而现有指标仅利用网络单向连边进行预测。文献[15]则是通过对网络中不同邻居结构下的连边概率进行统计并作为相似分值，在预测精度上取得了不错的效果。Valverde等[16]利用社交平衡理论研究证实了繁杂的人际关系将导致社交群体的不同演化方向等。张扬夫[17]曾受益于网络特性分析，提出一般化相似度指标，在共同邻居基础上提升了预测性能。然而，上述理论或方法仍无法使现有指标普遍适用于有向网络，缺少对局部邻居异构多样性的量化区分，且目前算法性能对比基准多采用无向网络局部相似性指标，该类指标中共同邻居含义在有向网络中已然发生改变。因此，有向网络的链路预测应当利用网络中多样的局部邻居异构形式进行预测。

针对上述问题，本文提出基于广义共同邻居的链路预测算法，通过分析网络中共同邻居有向异构体的具体作用，量化不同结构对连边产生的贡献程度，并结合连边概率将9种局部拓扑异构体进行融合，得到广义上的共同邻居计算方式，并基于此，针对有向网络重定义8种基于CN的相似性指标，使其有效利用共同邻居中有向连边信息并应用于有向网络。在12个真实数据集下实验对比，在AUC及Ranking Score衡量标准下所提方案大幅提升了预测准确度，验证了所提方案的有效性。

2 相关工作介绍

经典的CN算法认为两个节点间若存在更多共同邻居，则两节点更倾向于产生连边。若引入两节点度的影响，可从不同的角度衍生其他相似性指标，具体包括Salton[18]指标、Jaccard[19]指标、Sørensen[20]指标、HPI[21]指标、HDI[22]指标、LHN-I[23]指标。另外，考虑共同邻居节点的度时有Adamic-Adar[24]（AA）指标、资源分配[25]（RA，resource allocation）指标。在文献[26]中，杨瑞琪等将上述指标做了有向的变体使其尽可能适用于有向网络，一定程度上提高了在有向网络中的预测准确性，本节对其改进后的有向指标进行描述，同时为与其他较优的有向算法仿真对比，还列出PA[27]、LP[28]、Katz[29]这3种主流指标。现对相关指标及其有向方式的定义简介如下。

CN指标：以节点间共同邻居数目衡量连边可能性，表示为

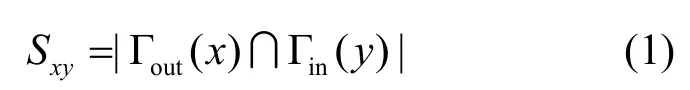
其中，Γout(x)表示节点x的出度邻居节点，Γin(y)表示节点y的入度邻居节点。

Salton指标：在共同邻居基础上引入端节点度信息，与端节点度之积开方成反比，表示为

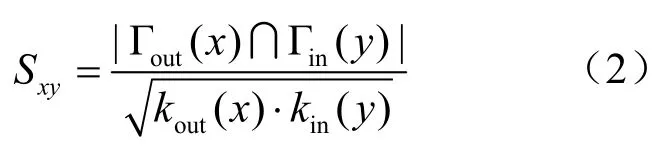
Jaccard指标：两节点邻居集合中共同邻居的占比，表示为

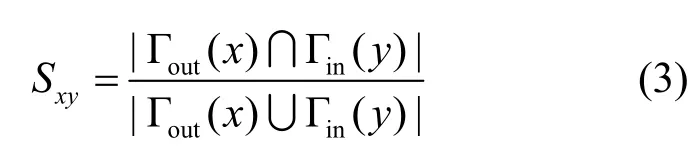
Sørensen：共同邻居与端节点的度之和之比，表示为

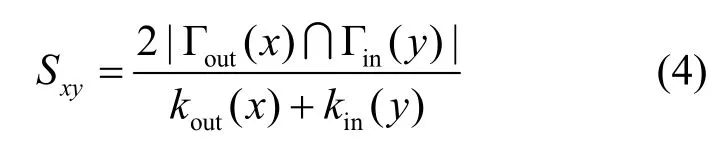
HPI指标：共同邻居与端节点最小度的比值，表示为

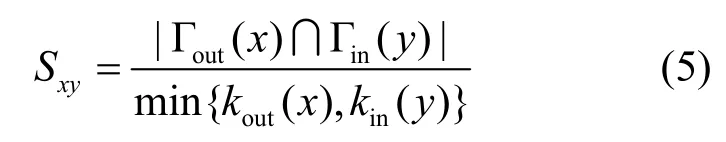
HDI指标：与HPI定义相似，表示为

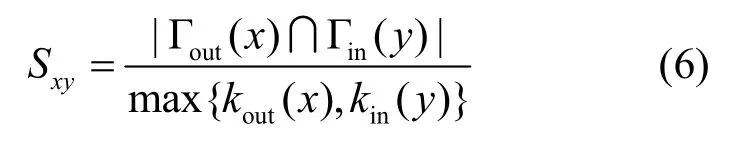
LHN-I指标：与Salton定义相似，分母为端节点度之积（相比之下没有开根号），表示为

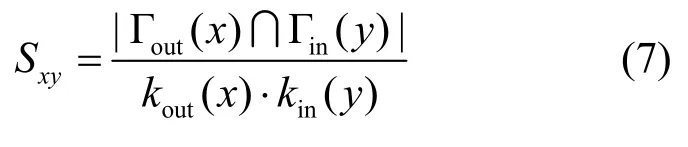
AA指标：考虑共同邻居节点度信息为共同邻居节点赋予权重，节点权重为节点度的对数分之一（度越大权重越小），表示为

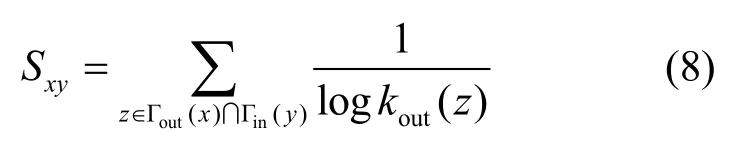
其中，kout(z)表示共同邻居z的出度。

RA指标：启发于资源分配过程，将共同邻居视为传递媒介，传递资源量与该节点的度成反比，表示为

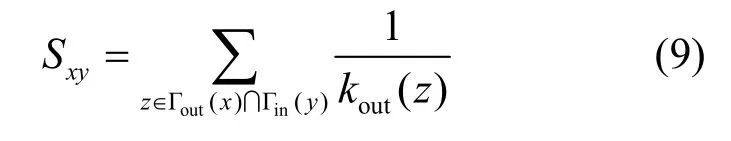
PA指标：节点与连边概率正比于二者度之积，表示为

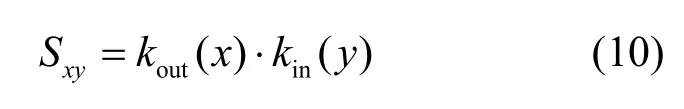
LP指标：在二阶共同邻居上考虑了三阶路径因素，表示为

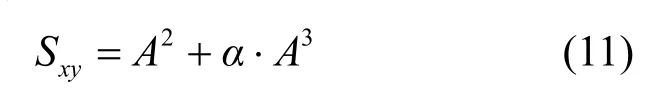
Katz指标：全局考虑网络所有路径，表示为

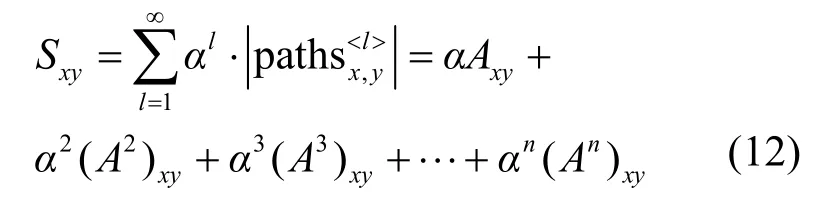
3 基于广义共同邻居的相似性算法

现有基于共同邻居的相似性指标在有向网络应用时，其共同邻居均定义为z∈Γout(x)∩Γin(y)，即节点对之间通过x→z→y的单向路径连接的邻居节点。而有向网络的局部结构远复杂于无向网络，连边方向的改变或互惠边的存在将使局部结构衍生多种异构形式。该共同邻居定义方式却缺失多样的有向异构连边信息，导致基于共同邻居的预测指标在有向网络预测普遍精度较低。潘永昊等[30]研究了网络内在结构的动力学特征，认为不同结构对新链路的产生效果不同。常圣等[31]研究发现，应用势理论筛选出有向网络中不包含互惠边的4种可定义势子图可显著提高有向链路预测的精度。

因此，共同邻居需面向有向网络进行重新定义，融合有向连边异构的多种局部拓扑对连边的贡献。

3.1 有向异构下的广义共同邻居融合表示

有向网络复杂性在于，节点x与y可通过出边、入边或互惠边的形式连接到共同邻居节点z，如图1所示，S1结构即节点x与y均经由互惠边连接到邻居节点z。而z∈Γout(x)∩Γin(y)仅是S9结构的单一表示，缺少对其他异构形式的充分利用。该定义中，Γout(x)表示x的出度邻居节点，可认为在S3、S8、S9结构中x→z的指向性节点对，Γin(y)表示y的入度邻居节点，即S5、S7、S9结构中z→y的指向性节点对。如此，其余8种异构形式的共同邻居均可通过改变连边指向进行描述，现将广义共同邻居（GMCN，generalized mutual common neighbor）定义如下。

定义1广义共同邻居：给定有向网络G(V,E)，其中，V代表网络节点集合，E代表网络中连边集合，该有向网络中两节点x与y的广义共同邻居定义如式（13）所示。

其中，Γbila(x)表示与节点x通过互惠边连接的邻居集合。

通过广义共同邻居定义方式，多样的有向异构形式均得到统一表述，保证了局部信息的充分利用。然而，将其应用预测算法时9类异构形式并非简单的数目作和。Brzozowski等[32]曾在社交网站WaterCooler研究发现，好友关注关系网络下，S7结构的数量最多，但产生连边比例最低；S1结构的数量最少，但连边比例最高，体现了互惠性在一些社交网络演化中的重要作用。但食物链网络中该现象却几乎不存在，而S9结构产生连边的比例最高，更加符合自然生物的层级捕食现象。

以C.elegans数据集为例进行具体分析，首先统计该数据集中上述9类结构数目，其次统计各结构下产生连边x→y的数目，计算得到各异构体独自的连边率，如表1所示。

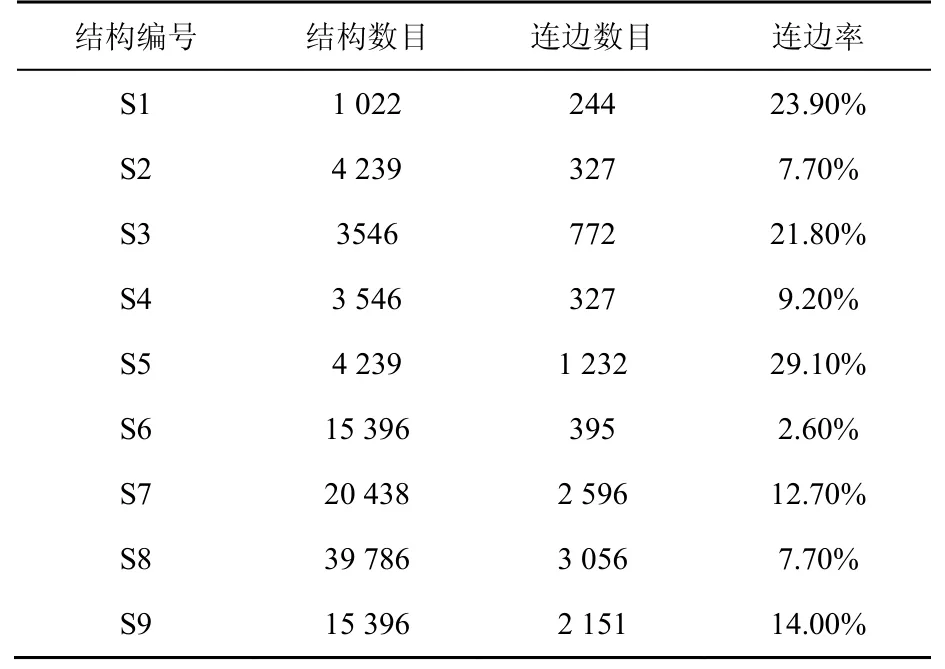
表1 C.elegans数据集不同异构体数目及连边率统计Table 1 Statistics of different isomers and edge rate of C.elegans

该数据集中，结构S8的数目最多为39 786，基于该种结构的连边x→y数目为3 056条，连边率仅7.70%；而结构S1总数目仅1 022，其连边数目却可达到244，连边率为23.90%。另外，结构S6与S9具有一致数目，二者连边率却相差极大，S9连边率已接近于S6的6倍，显然二者对连边产生的促进作用不等，该差异性难以在简单统计数目作和的计算方式下有效区分。且S6结构表现出一种“反向层级”现象，恰与原CN指标相反，这甚至会抑制新连边的产生，数目越大抑制作用越大。因此，结构数目并非连边产生的决定因素，其连边概率具有更加可信的参考价值。

对有向网络中共同邻居进行一般化定义后，通过上述连边率的分析，得出不同结构促进连边产生的贡献程度存在差异，因此将各个异构形式的连边概率作为其贡献程度权值，通过该贡献程度权值将各异构体进行融合计算，基于此将广义共同邻居算法（GMCN）定义如下。

定义2广义共同邻居算法：对于给定的有向网络G(V,E)，网络中任意两节点x与y之间的连边可能性计算为

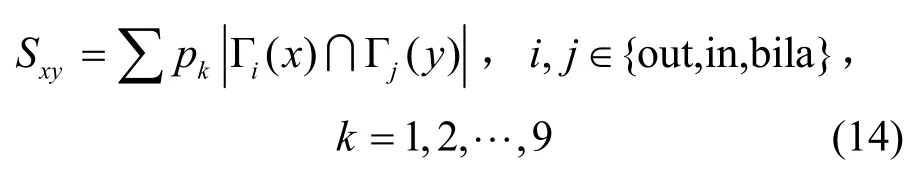
其中，pk表示9类结构在给定网络G(V,E)下的连边概率，pk计算方式定义如下。

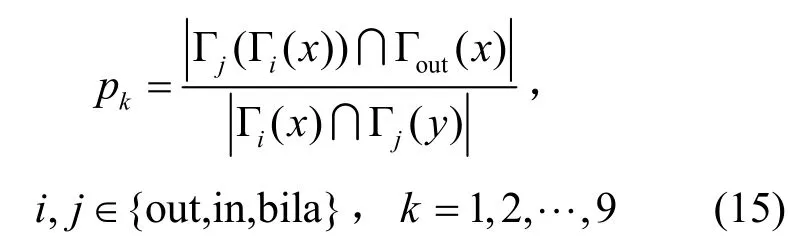
Γj(Γi(x))表示节点x的二阶广义邻居，Γj(Γi(x))∩Γout(x)表示节点x与二阶广义邻居直接相连的数目。

3.2 基于广义共同邻居的相似性算法

广义共同邻居的重新定义，有效涵盖了有向网络连边的多样异构形式，而现有指标中存在的覆盖不足问题得以解决。将广义共同邻居定义应用于现有基于共同邻居的相似性指标，重新定义基于广义共同邻居的相似性指标，将各指标重新表示如下。

GMJaccard：对Jaccard指标的重定义，将多样连边形式的邻居集合统一表述，量化区分，具体计算为

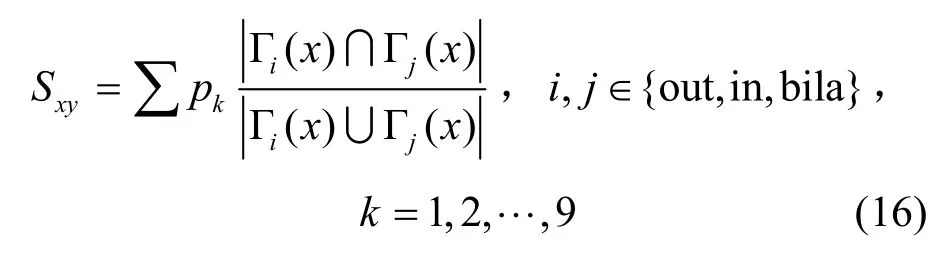
GMSalton：Salton指标的扩展，除应用广义共同邻居外，端节点的度同时进行了出入度等不同组合的统一表述，通过互惠边连接的共同邻居在计算时需采用该节点的出入度之和，具体计算为

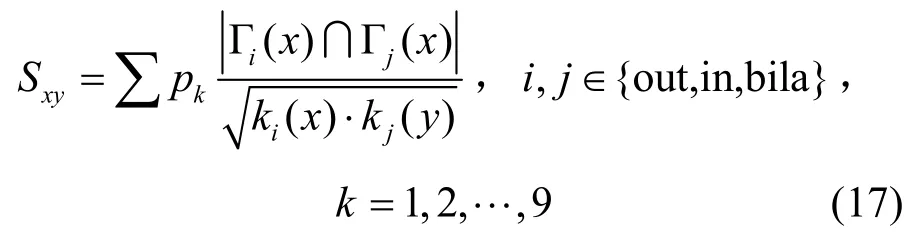
上述公式中kout(x)表示节点x的出度，kin(x)表示节点x的入度，kbila(x)表示节点x的出入度之和，下同。

GMSørenson：Sørenson指标的扩展，与GMSalton的扩展方式相同，移除原Sørenson指标分子中的乘数2，表示为

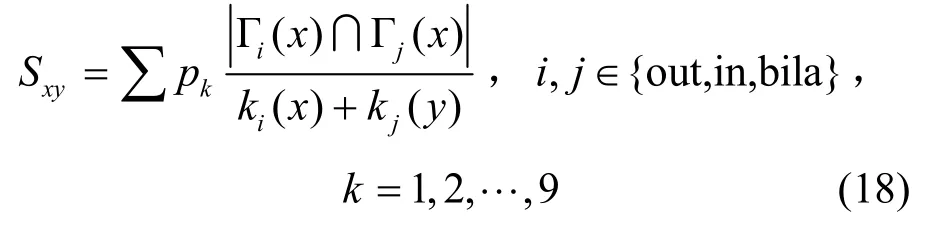
GMHPI：HPI指标的扩展，表示为

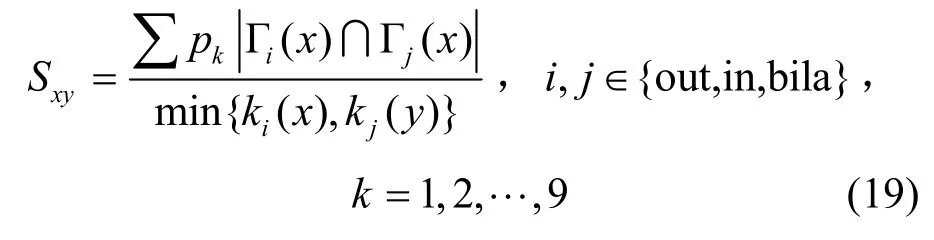
GMHDI：HDI指标的扩展，表示为

GMLHN：LHN指标的扩展，表示为

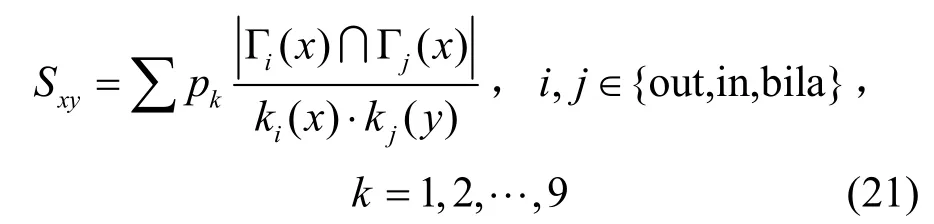
GMAA：AA指标的扩展，对广义下的共同邻居的出度进行加权计算，表示为

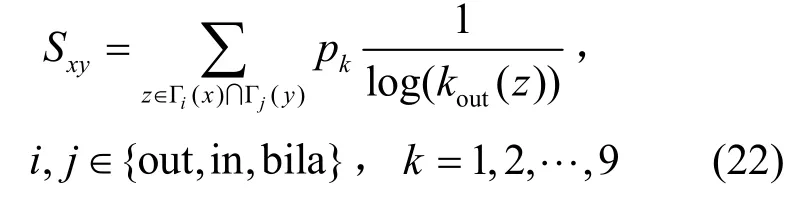
GMRA：与GMAA类似，是对RA指标的扩展，表示为

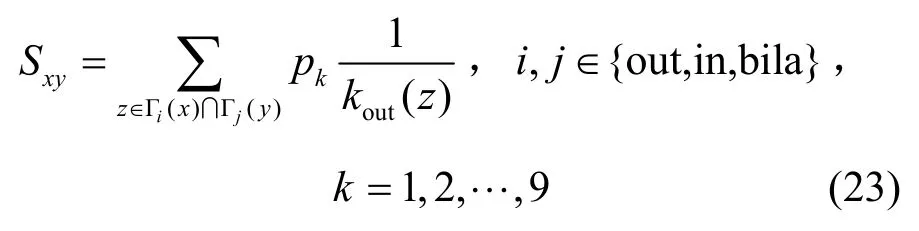
3.3 算法复杂度分析

CN指标因其简洁性著名，该指标及基于CN的算法计算复杂度为O(N3)[33]。基于GMCN的指标计算程序等同于9类有向邻居异构体的加权分值之和，因pk为各网络数据集的结构特性，已知的数据集网络连边确定，kp为固定值，仅对未知数据集首次计算时需统计S1～S9的连边概率，因此已知网络数据集计算复杂度为O(9N3)=O(N3)，继承了原指标低复杂度的优势。

4 评价指标及数据集介绍

4.1 评价指标

链路预测评价指在公认计算准则下对比不同算法的得分。通常将网络数据集E划分为训练集ET及测试集。以训练集数据预测测试集连边，以测试集和不存在边集计算评价指标得分，相似分值越高，连边概率越大。本文采用AUC[34]及Ranking Score[35]（RS）两种主流方式对所提方法进行衡量。

AUC可简单理解为在测试集中随机选择一条边的分数值比随机选择一条不存在边的分数值高的概率。从测试集TE和不存在边集中各随机选取一条边，比较二者的分数值，若测试集中的连边预测分数值高于不存在边集中的预测分数值累加1（n'表示），若二者相等累加0.5（n''表示）。AUC计算定义为

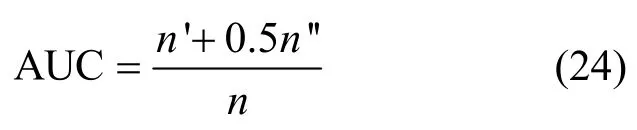
Ranking Score对所有未连边按照相似分值大小排序，得到测试集的边在最终排序中的位置，测试集连边排名越高，排序分值越小时，说明该算法具有较好预测性能。以H为未连边的集合（测试集中和不存在边集的集合），网络中某条测试边的排序分为

整个系统的排序分可通过遍历求得，计算方式如下。

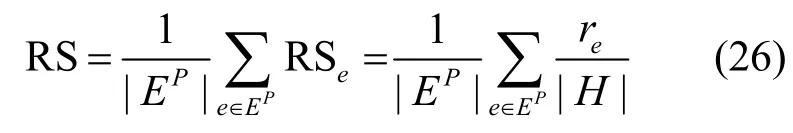
4.2 数据集介绍

为使实验验证具有代表性，本文选定12个有向网络真实数据集，涵盖社交网络、生物网络、引文网络、航空交通网络。数据集简介如下。

1)Highschool（HS）[36]：伊利诺伊州一所小型高中男生之间的友谊关系网络。

2)Residence hall（RH）[37]：澳大利亚国立大学校园217名居民之间的友谊关系网络。

3)Adolescent health（AH）[38]：美国青少年健康关系网络。

4)Physicians（PH）[39]：美国241名医生之间的相互朋友关系网络。

5)Usairport（UA）[40]：2010年美国机场之间的定向航班网络。

6)Openflight（OF）[41]：OpenFlights.org项目收集的航班网络。

7)C.elegans（CE）[42]：线虫神经元之间的突触连接关系网络。

8)SciMet（SM）[43]：引用“科学计量学”主题的论文引用网络。

9)Kohonen（KH）[43]：有关“自组织映射”主题或“Kohonen”的论文引用网络。

10)Wikivote（WV）[44]：维基选票网站的投票选举关系网络。

11)Chess（CH）[45]：国际象棋7 301个玩家之间的65 053场对战关系网络。

12)Air traffic control[45]（AC）：美国FAA飞行数据中心记录的规划航线网络。

预测实验时，设定训练集比例0.9，测试集0.1，每数据集进行50次独立实验，AUC及Ranking Score结果取其50次实验的均值。各数据集统计特征如表2所示，包括网络节点规模|V|、连边数目|E|、最大出度kout_max、最大入度kin_max、平均度＜k>、集聚系数C。

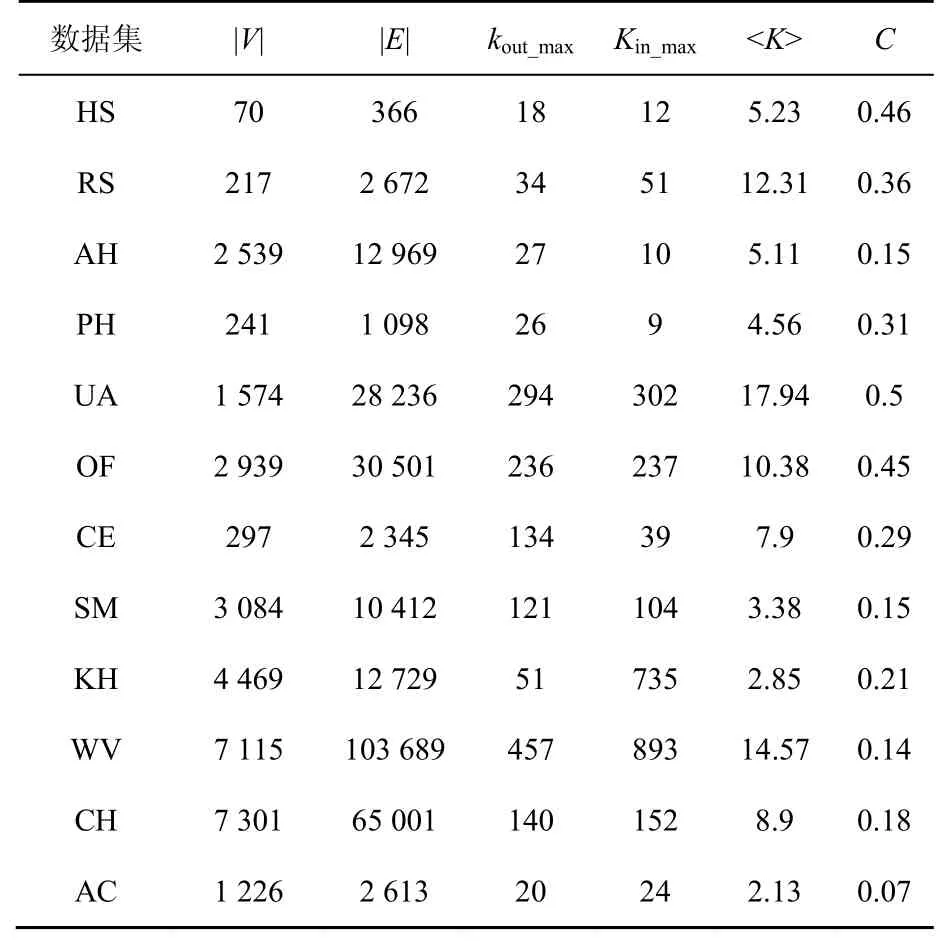
表2 数据集基本特征参数Table 2 Basic characteristics of datasets

5 实验验证及分析

为了验证方法的有效性，针对所提基于广义共同邻居的相似性指标，本节对比了现有指标有向方式的AUC及Ranking Score，验证该方案整体预测精度的表现。

5.1 AUC结果及分析

首先，GMCN指标AUC结果如表3所示。GMCN指标的AUC在12数据集上均有大幅度提升，在CH数据集上相比CN指标AUC提升幅度最大，由0.787提高至0.906。整体来看，社交关系网络中提升普遍较高，4种社交网络数据集的AUC平均提升8.23%，说明该类数据集中，错综复杂的局部连边结构中的潜藏信息可有效提高预测精度。PA、LP、Katz等指标虽在部分网络上表现突出，但其AUC值波动较大，如PA指标的“富者越富”机制在社交类网络中表现很差，AUC值低于0.7，甚至不及CN指标。LP指标考虑三阶路径因素，仅在航空、引文类网络具有轻微优势；Katz指标则考虑了全局路径信息，约在半数网络上略高于广义共同邻居方法，但其代价是付出极高的计算复杂度。因此，GMCN指标与CN复杂度相当，但与PA、LP相比却具有更高的精度，HS、RH、CE数据集上，该类指标甚至达到或高于利用全局路径信息的Katz指标的精度。

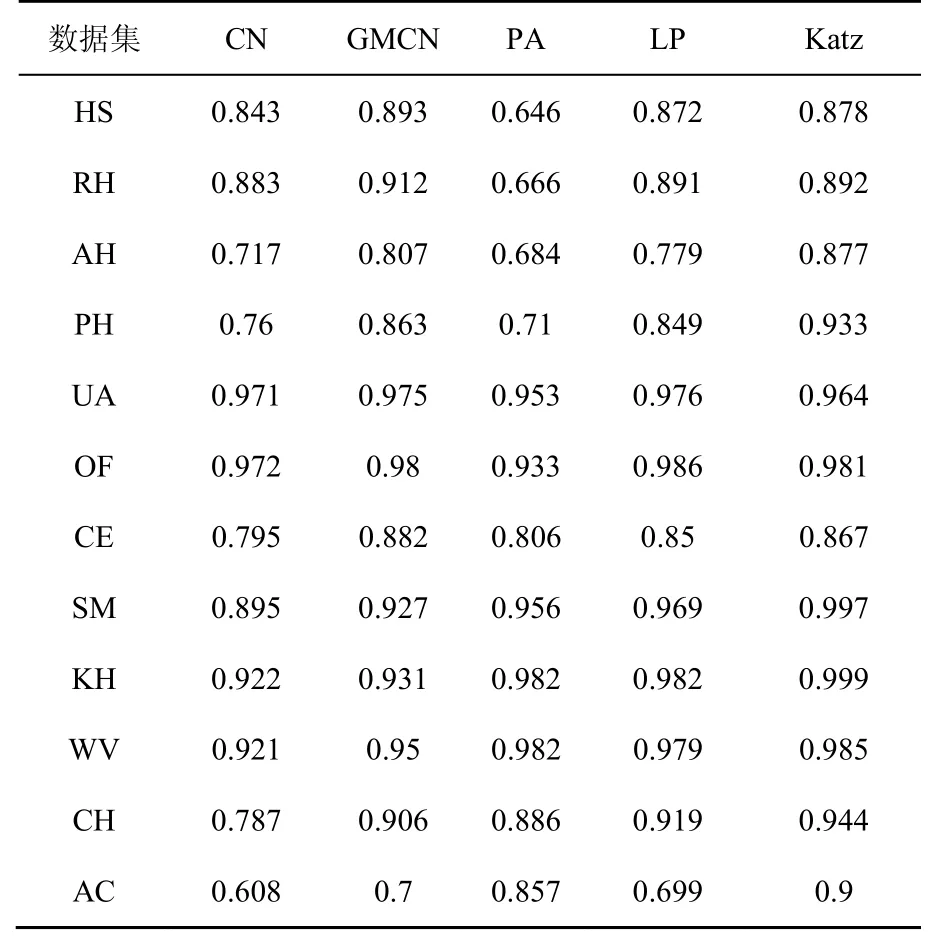
表3 AUC实验结果对比Table 3 Comparison of AUC results

其次，将广义共同邻居定义应用现有指标，得到基于GMCN的链路预测算法AUC结果，如表4所示。综合来看，在12个数据集上，重定义指标AUC值同样有大幅提升，各指标在社交类网络上提升明显，特别在AH数据集上AUC普遍由0.7提升至0.8之上，这一现象体现出社交平衡理论中多样的正负关系的确具有重要价值，现有指标仅通过单一的改进无法使经典指标适用于有向网络，应从结构上区分不同连边的异构体作用，从而有效提高预测精度。

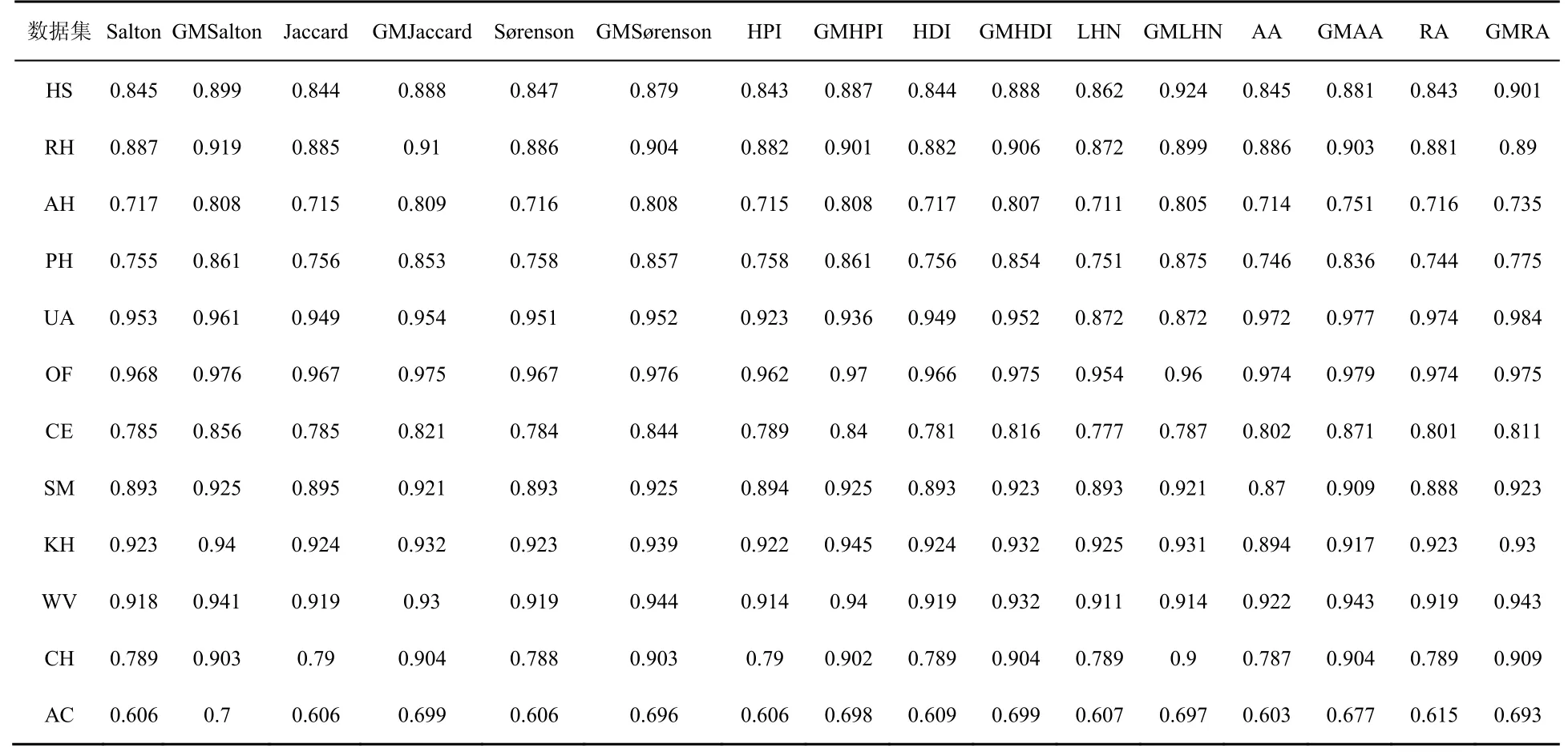
表4 基于GMCN的相似性指标AUC结果Table 4 AUC results of similarity index based on GMCN

纵向来看，各指标之间差异化并不明显，GMSalton、GMJaccard、GMSørenson、GMHPI、GMHDI、GMLHN指标与GMCN预测精度相当，AUC值保持在较小波动范围，这也同无向网络中该类指标预测效果相符。另外，采用局部节点度信息的AA、RA指标因仅计算到前述S9形式的共同邻居，疏漏其余8种异构邻居的度信息，除在航空网络有较高预测精度外，其余各类型网络不及0.9。而重定义优化之后的GMAA及GMRA则通过引入广义共同邻居，将数个网络的AUC值提升至0.9以上。

不同数据集中GM类指标与原指标AUC对比如图2所示。这里直观地显示了基于广义共同邻居的指标有效提升了AUC预测性能，在多种类型数据集的AUC值普遍保持在0.9上下，AH、PH及AC数据集上AUC值虽较低，但相比原指标，AUC提升近10%。GMCN指标相比CN指标提升效果最明显，在上述12个数据集上平均AUC提升6.01%，其余几种指标AUC值普遍提高5%左右，GMLHN指标稍有提升为0.47%。

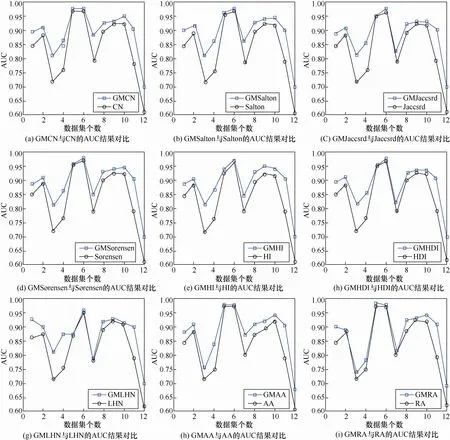
图2 不同数据集下GM类指标与原指标AUC结果Figure 2 AUC of GM-indexs and original indexs under different datasets

5.2 RS结果及分析

GMCN与CN的Ranking Score对比结果在表5中给出。首先从整体来看，GMCN指标的预测性能仍然全面优于CN指标，并且在社交网络上表现突出，相比CN指标的RS分值平均降幅为30.9%，低于PA及LP指标，在HS及RH等部分数据集上低于Katz指标，再次验证了基于GMCN的相似性指标在社交类网络的优良预测性能。另外，在UA、CE、WV、CH等数据集上GMCN也可与LP、PA、Katz主流指标达到相当的分值，体现了该类指标整体预测排名准确性的优势。

同时将GMSalton等8种基于GMCN的指标在12个数据集下RS分值在表6中进行对比。该8种指标RS得分普遍远低于原指标，均在各自网络数据集上表现出更好预测效果，同时相比AUC衡量标准对比优势更为突出。如在HS数据集上原指标RS分值由0.15降至0.09左右，优化指标的优势提升近40%，社交类网络整体降幅明显。其次，该类指标在WV投票网络、CH对战网络表现不俗，CH网络RS得分由0.14降至0.07。航空网络、生物网络上，该类指标在RS分值胜于原指标。GMRA及GMRA相比其他新指标降幅稍低，但已优于AA及RA指标，预测排名整体有了极大提升。因此，在RS分值评价方式下，基于广义共同邻居的相似性指标对于各种类型的网络数据均具有更好的预测表现。

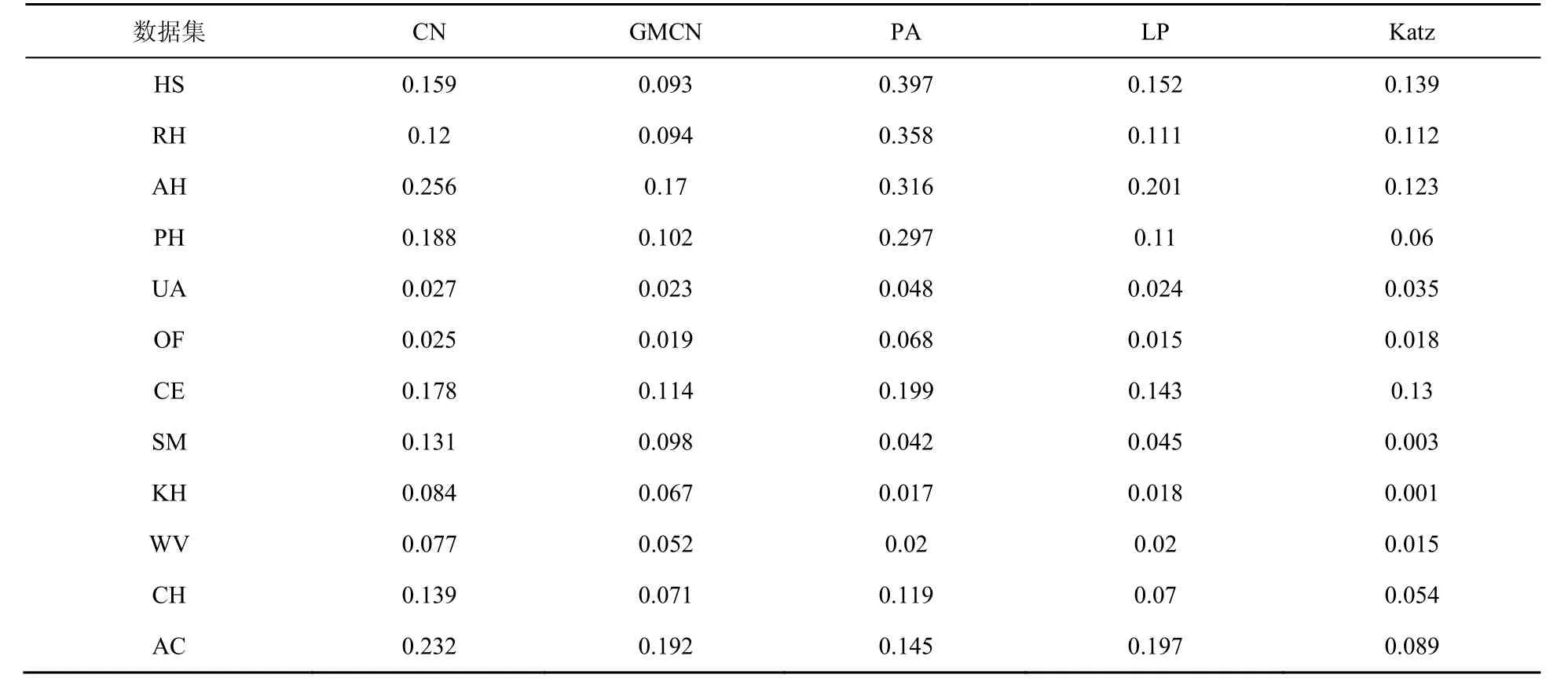
表5 Ranking Score结果对比Table 5 Comparison of Ranking Score results

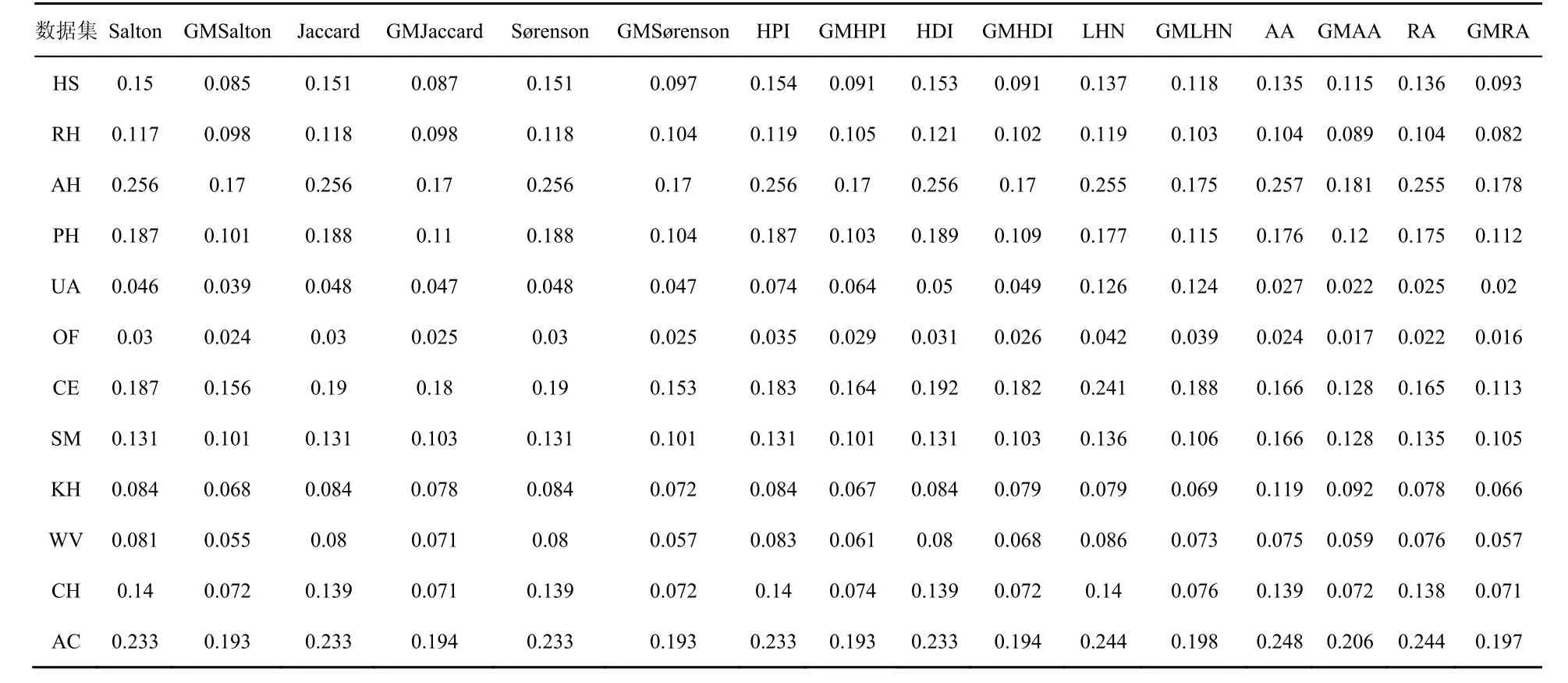
表6 基于GMCN的相似性指标Ranking Score结果Table 6 Ranking Score results of similarity index based on GMCN

各新定义指标与原有指标在12个数据集上的Ranking Score效果对比如图3所示。对比图2和图3可以直观看到，RS结果与AUC的提升效果基本相对应，其AUC值提升明显的网络的RS分值也更低。9个重定义的新指标在各数据集中的RS分值均在原指标曲线下方，说明数据集中的连边在整体排序中更为靠前。对于4种社交网络，GM类指标的RS分值平均降低30.9%，Physicians网络上RS分值降低了41%，效果最明显的国际象棋对战网络RS降低达48.3%。另外，几类网络的降低普遍在15%～20%，同样证实了基于广义共同邻居的相似性指标在RS评价指标下对不同网络的适用性。

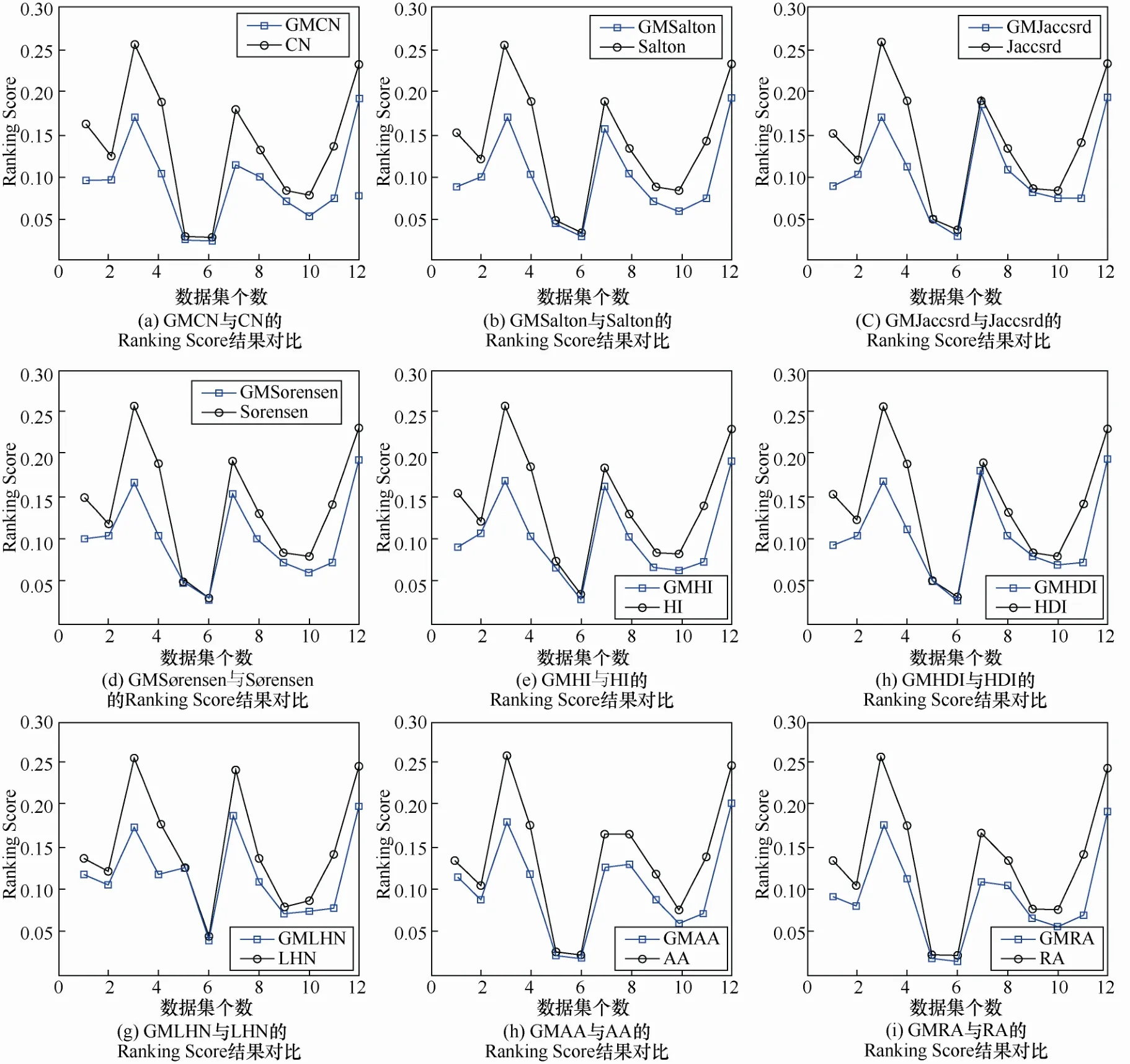
图3 不同数据集下GM类指标与原指标Ranking Score结果Figure 3 Ranking score of GM-indexs and original indexs under different datasets

6 结束语

本文针对有向网络中共同邻居存在多种有向异构形式，而现有指标缺少对多种异构形式下局部连边信息有效综合利用问题，提出了有向网络中广义共同邻居的定义，并基于广义共同邻居重定义了基于CN的8种相似性指标。以结构连边概率作为权重衡量促进连边的贡献程度使其针对多种类型网络具有普适性。十余个真实网络数据集仿真表明，广义共同邻居方式充分融合利用了共同邻居多种异构体间的局部结构信息，在AUC、Ranking Score衡量指标下，各新定义指标预测性能得到了大幅提升。此外该类方法继承了CN算法低复杂度的优势，适用较大规模网络链路预测。