晶体硅太阳电池应力的理论分析
2020-10-20黎之奇

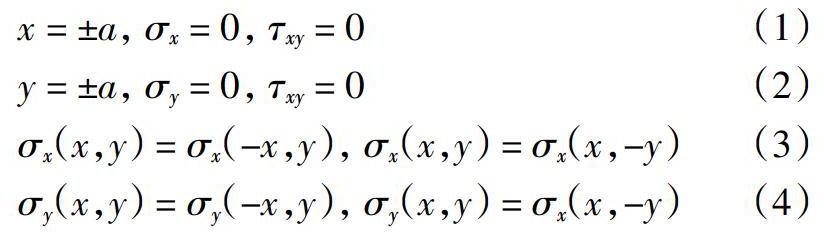

摘 要:光伏组件的电池层为一离散分布的不连续夹层. 针对组件中晶体硅电池片的受力特点导出了电池片的应力场和位移场,并对面板尺寸为1 580 mm × 808 mm的单晶硅标准组件在风荷载作用下晶体硅电池片的应力进行了计算和分析,考虑了风压及EVA胶膜的剪切模量变化对应力的影响. 计算结果与有限元结果进行了比较,并对比了125 mm × 125 mm和156 mm × 156 mm两种规格电池片的应力. 结果表明,理论结果与有限元结果符合很好,应力最大值出现在电池片的中点并随着EVA胶膜剪切模量的增加呈非线性增大;增大电池片的尺寸将引起应力的显著增加.
关键词:光伏组件;晶体硅电池;应力场;位移场
中图分类号:TU18 文献标识码:A
文章编号:1674—2974(2020)09—0137—07
Abstract:In photovoltaic (PV) modules, the solar cells are separated by small gaps and the stress distribution in cells is thus different from that where the cell layer is considered as a continuous one. In this paper, the solutions of the stress and displacement fields in the crystalline solar cells were developed. The stresses of the crystalline solar cells in PV module with a size of 1 580 mm × 808 mm were evaluated and the variation of the wind pressure and the effects of the storage shear modulus of the Ethylene-Vinyl Acetate (EVA) were considered. The results by the present solution were compared with those from Finite Element (FE), and the stresses of 125 mm × 125 mm and 156 mm × 156 mm cells were compared. The comparison shows that the results by present solution are in good agreement with those from the FE. The maximum stress (Von Mises stress) occurs at the middle of the cell and increases nonlinearly with an increase of the storage shear modulus of EVA. The results also show that the stress rises when the larger cells are applied.
Key words:photovoltaic(PV) modules;crystalline cell;stress distribution;distribution of displacement
光伏組件上的荷载主要是风荷载. 采用层压工艺制造的多层结构光伏组件,晶体硅电池片是离散的内埋于EVA胶层中,这种内埋形式一是给电池片的应变测量带来不便,二是给电池片的应力分析计算带来困难. 另一方面,EVA胶属于粘弹性材料,其储能剪切刚度与温度密切相关[1],在低温时剪切刚度大幅升高,从而引起电池片的应力增加. 我国地域辽阔,冬季南北温差很大,而现有的规范并未针对应用区域对组件的结构形式作出相关指引,因此在冬季严寒地区应用光伏系统时,由于风压而导致组件电池片出现隐裂和碎片等,使其经济效益大幅低于预期.
目前针对光伏组件的相关研究工作较少,主要集中在以下几个方面:1)外荷载(如风载等)作用时组件整体的强度研究[2,3];2)硅电池片在荷载作用下的机械强度及破坏特征[4-7];3)基于有限元法的电池片应力分析,以有限元方法研究组件在热循环作用下[8-11]及在荷载作用下[12]各层的应力和应变. 由于上述研究将电池层作为一连续夹层处理,与实际离散排列的、片间无相互作用的电池层不符.
对于内埋于EVA胶层的电池片,组件面板玻璃的变形将导致EVA胶层产生剪应变并将荷载传递至电池片. 文献[13]基于最小势能原理导出了光伏组件晶体硅电池片的位移场及应力场,由于位移分量取为重三角级数形式,其计算结果在电池片边缘处的Von Mises等效应力为零. 文献[14]基于Ansys分析了组件电池片的应力分布,表明处于双向拉伸状态的电池片边缘处的Von Mises等效应力不为零. 对于晶体硅电池片应力的正确描述目前尚无相应的理论解.
本文针对光伏组件晶体硅电池片的受力特点导出了光伏组件晶体硅电池片应力场和位移场的级数解,计算了组件在不同风压及EVA胶膜弹性模量发生变化时晶体硅电池片的应力分布. 计算结果与文献[14]的有限元结果进行了比较,验证了理论解的正确性,并对广泛应用的125 mm × 125 mm和156 mm × 156 mm两种主流电池片进行了讨论. 本文的理论解对光伏组件在不同风荷载及环境温度下晶体硅电池片的应力分析提出了理论计算方法,为光伏工程设计提供了依据.
1 电池片理论分析简化模型
图1为目前分体式光伏组件的主流构造形式,依次为3.2 mm超白钢化玻璃面板、0.5 mm的EVA胶膜、0.19 mm的晶体硅电池片、0.5 mm的EVA胶膜、0.35 mm的TPT背膜,经层压后形成的多层组合结构. 电池片则离散地分布于EVA胶层中,片与片的间距约1 ~ 2 mm,之间仅有两条宽约3 mm,厚约0.1 mm的金属片作為电气连接,因此电池层可看成一离散的、片与片之间无相互作用的薄层. 组件受外荷载作用而弯曲变形时,EVA胶层发生剪切变形,将荷载传递至电池片表面,在电池片内产生应力.
考虑电池片的受力情况,本文的理论分析基于以下的简化模型:
1)垂直于电池片表面的正应力σz与电池片的面内应力分量相比很小,可忽略;
2)组件弯曲时,电池片表面的荷载来自于上下表面EVA胶膜的剪应变,而EVA胶膜的剪应变则由面板玻璃及TPT背膜与电池片的变形差异引起. TPT背膜是厚度约0.35 mm的聚氟乙烯复合膜,弹性模量比硅电池片低约2个数量级,其变形在电池片范围内将受到电池片的约束,因此忽略TPT背膜对电池片下表面的作用;
3)忽略EVA胶对电池片端面沿厚度方向的作用;
4)电池片的厚度仅为0.19 mm,可以看成一偏离组件中性面的离散薄层,组件弯曲时电池片处于整体双向受拉和弯曲的组合作用,其中弯曲应力是次要的,因此以下的分析忽略电池片的附加弯曲应力,认为面内应力沿厚度方向不变;
5)组件的面板玻璃尺寸一般比电池片的尺寸大一个数量级,因此近似认为面板玻璃下表面的应变在电池片范围内为常数.
取图2所示的坐标系,基于上述的简化模型及对称性可给出如下的应力边界条件和对称关系:
2 电池片的应力场和位移场
图3所示为按简化2)和3)由组件中取出仅包含一片电池的层合板计算单元沿x方向的变形示意图,与电池片相对应的面板玻璃底面在x方向的正应变值为 ε gx . 组件发生弯曲变形时,电池片上表面由于受到EVA胶的剪应力作用在x方向产生位移ux. 不考虑在变形过程中EVA胶层的厚度变化,且在小变形时认为EVA胶的应力应变近似服从线性关系,则任一点x处EVA胶层的剪切应变为
式中:δ为组件的弯曲中面至面板玻璃底面的距离;b为EVA胶层的厚度.
作用于电池片上表面沿x轴方向的分布面荷载px可表示为
式中:GEVA为EVA胶的储能剪切刚度. 同理,沿y方向的分布面荷载py可表示为
式中:ε gy 为与电池片相对应的面板玻璃底面在y方向的正应变值;uy为电池片上表面由于受到EVA胶的剪应力作用在y方向产生的位移. 面荷载分量px、py是位移分量ux、uy的函数.
考虑一长度和宽度分别为dx和dy、厚度为t(电池片厚度)的电池片单元体如图4所示,根据简化4),忽略电池片的附加弯曲应力,认为电池片的应力沿厚度方向不变. 则不考虑体力时单元体沿x和y方向的平衡方程为
3 算例及结果
3.1 与有限元结果比较
文献[14]基于Ansys对面板尺寸为1 580 mm ×808 mm的195 W单晶硅标准组件在风荷载作用下组件中点处晶体硅电池片的应力进行了计算和分析,考虑了不同风压及EVA剪切模量变化对应力的影响,本文结果与文献[14]的有限元结果进行比较. 以本文的解答对面板尺寸为1 580 mm × 808 mm的195 W单晶硅标准组件进行了相同计算,该组件坐标系取为x轴沿组件短边方向,y轴沿组件长边方向,组件在风压标准值分别为0.50、0.65、0.80、0.95、1.10 kN/m2时面板玻璃中点处下表面的应变值εxg、εyg 如表1所示[13].
处于双向拉伸状态的电池片,以Von Mises等效应力σeq来衡量电池片内一点处的应力
光伏组件的EVA胶属于粘弹性材料,其储能剪切刚度随温度的变化较大. 研究表明[1],在60 ℃时的GEVA约为3 MPa. 而温度降低至 -20 ℃时则大幅增加至约40 MPa. 因此计算电池片应力时应考虑GEVA的变化.
以本文理论模型计算了上述组件在风压为0.65 kN/m2作用下,EVA胶膜的储能刚度GEVA = 10 MPa时电池片Von Mises等效应力沿x轴和y轴的变化如图5所示,并与文献[14]的相应结果进行比较. 电池片的各计算参数取为:E = 180 GPa,μ = 0.27,a = 62.5 mm,t = 0.19 mm,b = 0.5 mm.
在组件的工作温度范围内,EVA胶所呈现的弹性模量比玻璃的弹性模量(72 GPa)低约3个数量级,而电池片是离散地分布于EVA胶层中. 有限元结果表明,EVA胶层、TPT背板和电池的组合层对组件的整体刚度影响很小,组件弯曲时近似以面板玻璃的中性面弯曲变形[14],因此计算时组件的弯曲中面至面板玻璃底面的距离δ取为1.6 mm.
图5的结果表明:1)最大应力均出现在电池片中点,与有限元结果比较,本文理论结果的最大应力值偏低约2.51%;2)沿x轴方向的应力在边界处本文结果略高于有限元结果,而沿y轴方向则始终低于有限元结果. 电池片应力沿x轴的变化较大,而沿y轴的变化较小.
当EVA胶剪切模量GEVA由2 MPa变化至40 MPa,组件面板风压值分别为0.50、0.65、0.80、0.95、1.10 kN/m2时,以本文理论模型计算的电池片中点处最大等效应力如图6所示,文献[14]的结果也列于图中进行比较. 由图6可以看出,二者的结果符合较好,但本文的结果始终低于有限元结果,其原因是本文的理论模型忽略了TPT背膜对电池片的影响.
3.2 電池片尺寸的影响
随着晶体硅技术的发展,156 mm × 156 mm的大尺寸晶体硅电池片已在光伏组件中得到广泛应用. 目前的156 mm × 156 mm电池片组件仍采用3.2 mm面板玻璃,在相同风压下电池硅片的应力将有所提高.
以本文理论模型计算的两种规格电池片组件在组件尺寸及各计算参量相同的情况下,风压值为0.65 kN/m2时电池片中点处等效应力随EVA胶层剪切模量GEVA的变化如图7所示. 结果表明,电池片尺寸的增加将引起应力较大幅度的上升,从而电池片破裂的隐患增加. 因此,采用大尺寸电池片的组件应适当增加面板玻璃厚度,提高组件的整体弯曲刚度,可有效降低电池片的应力.
4 结 论
1)针对光伏组件晶体硅电池片的受力特点导出了晶体硅电池片应力场和位移场的级数解答. 对尺寸为1 580 mm × 808 mm的195 W单晶硅组件面板中心处电池片的应力进行了计算并与文献[14]基于Ansys的有限元结果进行了比较. 结果表明二者符合很好.
2)比较了125 mm × 125 mm和156 mm × 156 mm两种规格电池片组件在风压为0.65 kN/m2时的应力,结果表明电池片尺寸的增加将导致应力的增大. 因此在光伏系统设计时应充分考虑当地的气象数据,并结合应力分析计算,选用合理的组件.
3)现行光伏规范中并未考虑EVA胶层储能剪
切刚度随环境温度的降低而增大,从而引起电池片应力的升高. 这种对安装地区不加区分的应用,导致在冬季严寒地区安装的光伏系统其电池片由于高应力而出现性能过早衰退. 因此在相关规范的修订中建议将环境因素(温度、风压)纳入指引.
参考文献
[1] EITNER U,KAJARI-SCHRODER S,KONTGES M,et al. Non-linear mechanical properties of Ethylene-Vinyl Acetate(EVA) and its relevance to thermomechanics of photovoltaic modules[C]//Proceeding of 25th European Photovoltaic Solar Energy Conference. Valencia,Spain,2010:1—3.
[2] JUBAYER C,HANGAN H. Numerical simulation of wind loading on photovoltaic panels[C]//Proceeding of Structures Congress. Chicago,Illinois,USA,2012:1180—1189.
[3] COSOIU C I,DAMIAN A,DAMIAN R M,et al. Numerical and experimental investigation of wind induced pressure on photovoltaic solar panel[C]//Proceeding of 4th IASME/WSEAS International Conference on Energy,Environment,Ecosystems and Sustainable Development. Algarve,Portugal,2008:74—80.
[4] SCHONFELDER S,BOHNE A,BAGDAHN J. Mechanical strength of mono and multicrystalline wafers[C]//Proceeding of 18th Workshop on Crystalline Silicon Solar Cell & Modules. Material and Processes 2008,Vail Cascade Resort,Vail,Colorado,USA,2008:187—190.
[5] ROZGONYI G,YOUSSEF K,KULSHRESHTHA P,et al. Silicon PV Wafers:Mechanical strength and correlations with defects and stress[J]. Solid State Phenomena,2011,178/179:79—87.
[6] CERECEDA E,BARREDO J,GUTIERREZ J R,et al. Mechanical stability in crystalline silicon solar cells[C]//Proceeding of 5th World Conference on Photovoltaic Energy Conversion. Valencia,Spain,2010:1665—1668.
[7] PINGEL S,ZEMEN Y,FRANK O,et al. Mechanical stability of solar cells within solar panels[C]//Proceeding of 24th European Photovoltaic Solar Energy Conference. Hamburg,Germany,2008:3459—3463.
[8] 王曉燕,耿洪滨,何世禹,等. 热循环下太阳电池板单元结构热应力演变规律研究[J]. 太阳能学报,2007,28(4):345—350.
WANG X Y,GENG H B,HE S Y,et al. Thermal stress study of solar PV module structure[J]. Acta Energiae Solaris Sinica,2007,28(4):345—350. (In Chinese)
[9] 王晓燕,耿洪滨,何世禹,等. 热循环作用下太阳电池板单元结构寿命预测[J]. 太阳能学报,2007,28(6):583—586.
WANG X Y,GENG H B,HE S Y,et al. Life forecast of element structure of solar panel under thermal cycles[J]. Acta Energiae Solaris Sinica,2007,28(6):583—586. (In Chinese)
[10] CAO M,BUTLER S,BENOIT J T,et al. Thermal stress analysis/life prediction of concentrating photovoltaic module[J],Journal of Solar Energy Engineering,2008,130:1—9.
[11] EITNER U,PANDER M,KAJARI-SCHRODER S,et al. Thermomechanics of PV modules including the Viscoelasticity of EVA[C]//Proceeding of 26th European Photovoltaic Solar Energy Conference and Exhibition. Hamberg,Germany,2011:3267—3269.
[12] 封忠江,晏石林,陈刚. 光伏组件机械载荷试验及数值模拟研究[J]. 固体力学学报,2014,35(S):251—255.
FENG Z J,YAN S L,CHEN G. Mechanical load experiments on PC module and its numerical simulation[J]. Chinese Journal of Solid Mechanics,2014,35(S):251—255. (In Chinese).
[13] 黎之奇. 光伏组件晶体硅电池片应力分析[J]. 太阳能学报,2015,36(6):1493—1498.
LI Z Q. Stress analysis of crystalline silicon solar cell in PV module[J]. Acta Energiae Solaris Sinica,2015,36(6):1493—1498. (In Chinese)
[14] 黎之奇,杨非池. 基于ANSYS的光伏组件晶体硅电池片应力分析[J],湖南大学学报(自然科学版),2016,10(11):149—153.
LI Z Q,YANG F C. Stress analysis of crystalline cell in PV modules using ANSYS[J]. Journal of Hunan University(Natural Sciences),2016,10(11):149—153. (In Chinese)
