模糊质量损益函数模型及其过程均值设计优化

聂相田， 刘 晨， 郭伟杰， 刘梦琪，3， 王 博

（1.华北水利水电大学水利学院，郑州 450046； 2.河南省地质矿产勘查开发局第二地质矿产调查院，郑州 450001；3.黄河勘测规划设计研究院有限公司，郑州 450003； 4.水资源高效利用与保障工程河南省协同创新中心，郑州 450046；5.河南省水环境模拟与治理重点实验室，郑州 450046）

为了量化质量波动产生的损失，Taguchi［1］在1985年提出了质量损失函数理论；Zebek等［2］针对质量损失函数模型的无界性，提出了倒正态分布函数；张素梅［3］利用择近原则，将模糊数学中的贴近度及隶属度函数等与容差成本模型融合，设计出了一种模糊容差稳健优化设计的方法；曹衍龙等［4］基于模糊理论提出了模糊质量损失的概念，建立了模糊质量损失函数模型；赵延明等［5］利用分段理论对田口损失函数加以扩展，建立了一种新的质量损失函数模型；潘尔顺等［6］对田口损失函数进行了修正，建立了非对称的田口损失函数模型；张月义等［7-8］提出了在不忽略一次项损失的情况下，二次式望小、望大特性质量损失函数模型；刘远等［9］针对复杂产品多阶段生产过程中外购系统质量特性的容差调整与修正问题，构建了复杂产品的质量容差优化模型.

王博等［10-12］针对质量损失函数无法描述生产实践中存在的质量补偿效果，将泰勒级数展开式中常数项定义为质量补偿，提出了质量损益函数的概念，研究了质量损益传递模型及质量特性的容差优化方法，并且在一次项损失不能忽略且补偿量恒定时，设计了望大望小特性质量损益函数模型. 质量的好坏难以量化，产品质量的定义与评价总是存在一定的模糊性. 在工程实际中给出质量特性目标值允许的范围，当产品的质量特性目标值在波动范围内时，产品的质量损失为0，若产品质量特性值超出了波动范围，则产品质量损失不为0. 例如，零件能够承受的压强为50 MPa，若压强刚好为50 MPa时质量损失为0，若压强增大到50.01 MPa时就认为存在质量损失. 这种严格按照标准规定的原则看似绝对公正，但与工程实际不符. 因此结合模糊理论与质量损益函数，提出了模糊质量损益函数理论.

针对质量损益函数的非对称性，Springer等［13］在望目特征质量损失函数的上下规格明确的情况下，对最优过程均值进行了确定；Ho等［14］在非对称的二次质量损失函数的基础上，考虑了过程能力不足的因素，确定了最优过程均值；Phillips等［15-16］针对过程输出分布存在偏差的情况，建立了非线性规划模型求最优过程均值.

陈湘来等［17-18］在讨论了非对称质量损失函数的基础上，构造出质量特性目标均值与标准差的优选模型，进而得到最优目标过程均值与标准差. 魏世振等［19］提出了过程有效偏移及质量损失率两个概念，讨论了利润最大化的过程均值设计问题；倪自银等［20］研究了三种典型的非对称损失的最优过程均值设计问题；金秋［21］研究了非对称质量损失的三角分布过程均值的优化问题.

在产品的生产和制造过程中，由于随机因素或系统因素，使产品质量偏离目标值，造成损失. 例如，在零件加工中，当加工的零件尺寸大于目标值时，可通过加工进一步对损失进行补偿，降低质量损益；但零件的尺寸小于目标尺寸时，则无法补救只能按照作废处理，损益是非对称的. 在这种情况下，零件加工出的产品均值与目标值相等并不会使期望损益最小，要使加工的过程处于稳定状态就要对过程均值与容差进行设计，使其参数处于预定的范围内. 又如，某一产品的包装上标明其净含量为1000 g，即产品的目标值为1000 g，当净重量超过1000 g时，是对厂家造成了经济损失，当净重少于1000 g时，对厂家造成的是信誉上的损失，显然，超出目标值或低于目标值所造成的损益不相同. 因此，过程均值设计研究具有实际意义.

1 模糊质量损益函数模型建立

1.1 质量损益函数

王博等［11］提出了质量损益函数的定义，设产品的质量特征值和目标值分别为y 和y0，相对应的质量损益为G(y)和G(y0)，若G(y)在y=y0处存在二阶导数，则按照泰勒级数展开有

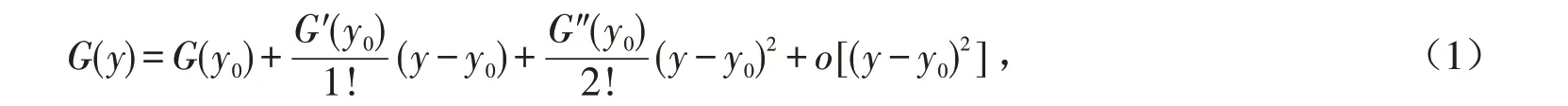
式中，当y=y0时，质量损益G(y)等于极值G(y0)，即G′(y0)=0. 由于存在质量补偿，故G(y0)∈R. 略去二阶以上的高阶项，得到

其中，k=G″(y0)/2!为常数，G(y0)表示质量补偿，质量损益函数图像( )G(y0)＜0 如图1所示.

当G(y0)＜0 时，质量波动引起的损失小于质量补偿；当G(y0)＞0 时，质量波动引起的损失大于质量补偿；当G(y0)=0 时，质量波动引起的损失等于质量补偿. 一般可根据功能界限Δ0和丧失功能的损失A0或容差Δ和不合格损失A 确定k . 如式（3）及如图2所示.

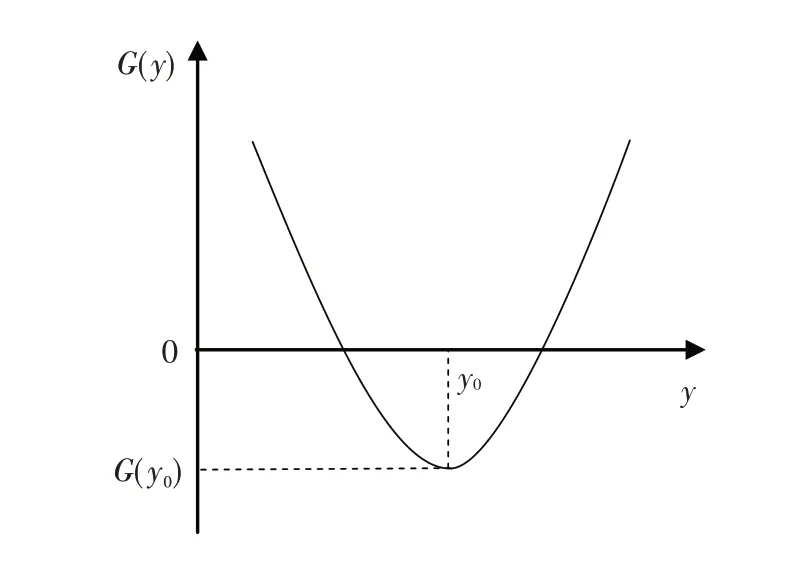
图1 质量损益函数图像( )G(y0)＜0Fig.1 Image of quality gain-loss function(G(y0)＜0)

图2 k的确定方法( )G(y0)＜0Fig.2 Determination of k(G(y0)＜0)

式（2）表示质量补偿恒定时的质量损益函数，则当质量补偿不为恒量时，可以令质量补偿为质量特性y的函数，记为质量补偿函数g(y)，此时可记质量损益函数为

同理可得出望小特征质量损益函数GS(y)及望大特性质量损益函数GL(y)分别为

1.2 模糊质量损益函数

令望目产品的质量特性最大损益值为Gmax，定义事件A：产品的质量损益为G(yk)，令质量特性y 对事件A 的隶属度为y 的模糊质量损益，y 对事件A 的隶属函数作为y 的模糊质量损益函数.

若G(yk)=Gmax，G˜(yk)=1；若G(yk)=Gmin，G˜(yk)=0；若G˜min＜G(yk)＜Gmax，G˜(yk)∈(0,1).

对于不同的质量特性应具有不同形式的模糊质量损益函数，设计者可根据工程实际情况选取适当的模糊损益函数，使其设计目标更加接近工程实际，如梯形分布望目特性模糊质量损益函数.

质量特性y的目标值y0和容差Δ 存在一定的模糊性. 给定Δ1和Δ2，且0 ≤Δ1≤Δ ≤Δ2，当 ||y-y0≤Δ1时对事件A的隶属度为0，当 ||y-y0＞Δ2时对事A的隶属度为1，梯形分布望目特性模糊质量损益函数如图3所示.

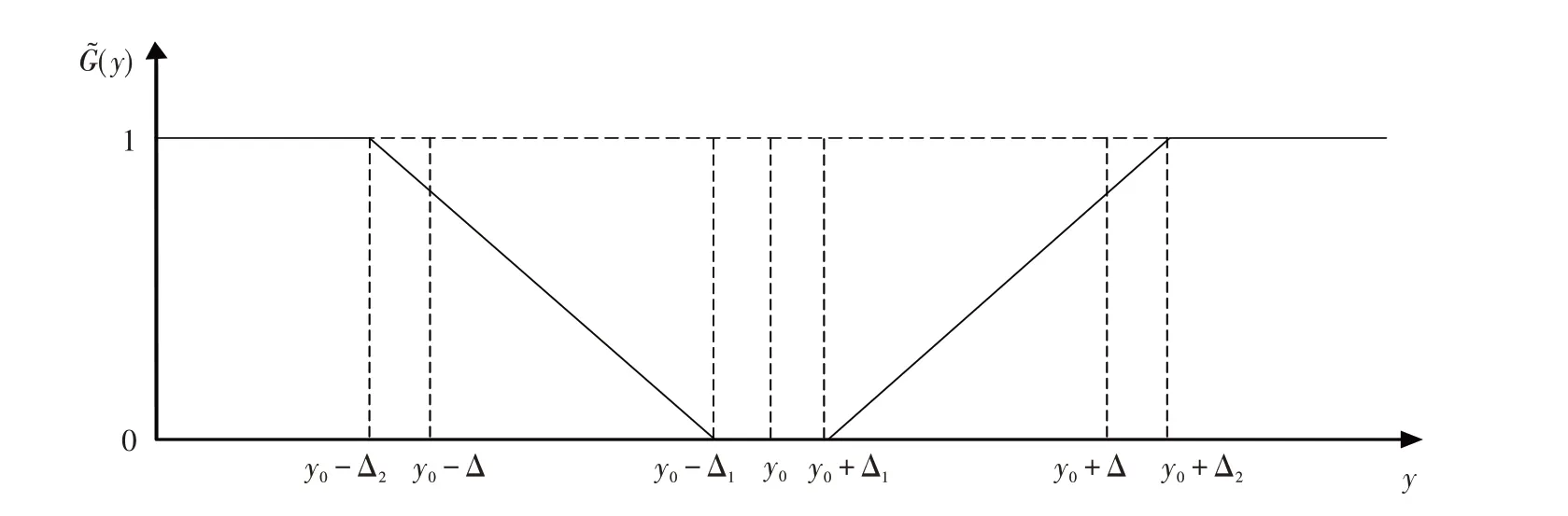
图3 梯形分布望目特性模糊质量损益函数Fig.3 Fuzzy quality gain-loss function with trapezoidal distribution

同理，对于望大质量特性，当y ≥ ||y0-Δ1时，对事件A的隶属度为0，而y ＜ ||y0-Δ2时，对事件A的隶属度为1；对于望小质量特性，当y ≤ ||y0+Δ1时，对事件A 的隶属度为0，而y ＞ ||y0+Δ2时，对事A 的隶属度为1.梯形分布望大特性模糊质量损益函数如图4所示，梯形分布望小特性模糊质量损益函数如图5所示.

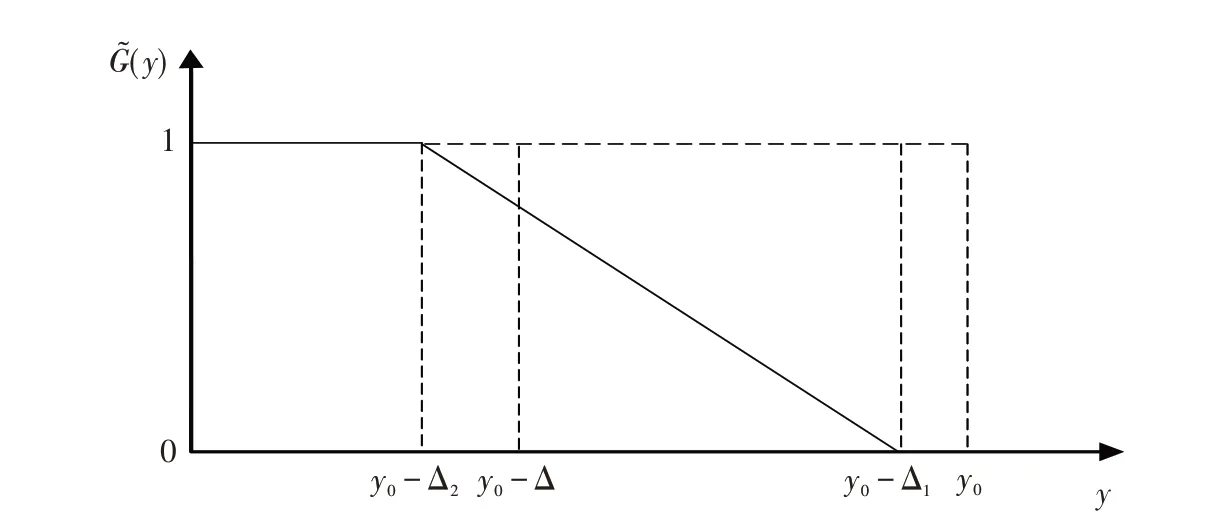
图4 梯形分布望大特性模糊质量损益函数Fig.4 Fuzzy quality gain-loss function with larger-the-better characteristic of trapezoidal distribution

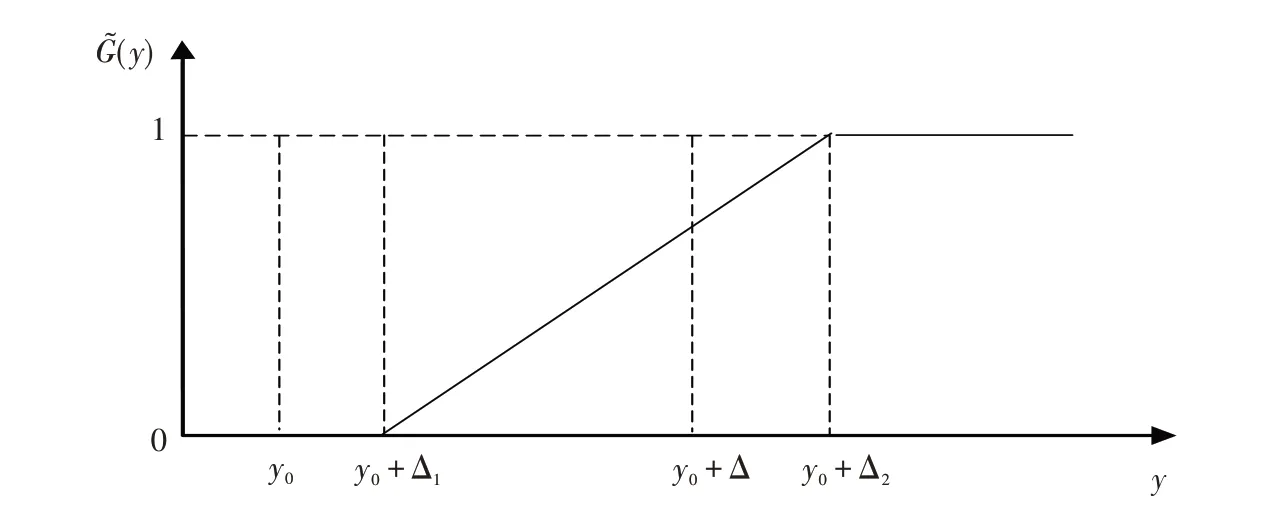
图5 梯形分布望小特性模糊质量损益函数Fig.5 Fuzzy quality gain-loss function with smaller-the-better characteristic of trapezoid distribution

1.3 模糊质量损益函数模型的特点

1）与质量损益函数相比，模糊质量损益函数具有更大的实用性和灵活性，模糊质量损益函数定为

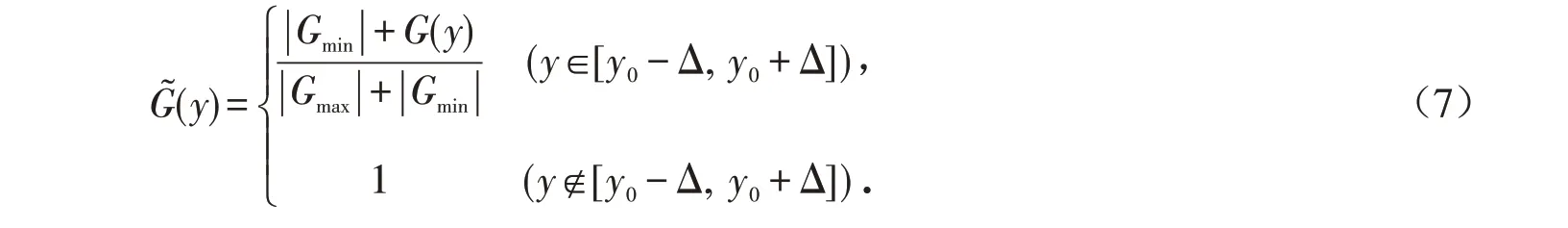
这时质量损益函数与模糊质量损益函数的图像在区间［y0-Δ，y0+Δ］有相同的变化趋势，但模糊质量损益函数将模糊损益值限定在0～1之间，在区间外的模糊损益值被限定为最大值1. 因此，模糊质量损益函数可以作为质量损益理论的一种推广形式.

2）由于将质量目标值y0和容差Δ进行了模糊处理，质量特性的波动范围被适当放宽了，与质量损益函数具有无穷大的情况不同，模糊质量损益有明确的界限（介于0～1之间），因此可适当地增加容差大小，降低产品的加工成本，也能提高产品的可加工性.

3）将模糊质量损益限定在0～1的区间内，使得各质量特性之间具有可比性.

2 非对称模糊质量损益函数的过程均值设计

2.1 一次非对称模糊质量损益函数过程均值设计

假设产品的质量特性值y 服从正态分布N(μ,σ2)，在生产的工序过程未调整之前，其输出均值μ 与目标值y0一致. 根据模糊质量损益函数定义，以梯形分布的非对称线性模糊质量损益函数为例，关于模糊质量特征y的模糊质量损益函数为

其模糊质量损益函数的模糊期望损益为

可知F1(δ)是E[L1(δ)]归类化简后的函数，两者实质是同一个函数，且具有相同的极值点. 求F1(δ)关于δ 的一阶微分，并令其等于零，可得出F1(δ)的所有极值点.

由于E[L1(δ)]与F1(δ)有相同的极值点δ1，再由δ=得出μ1=δ1σ+y0，即μ1为模糊最优均值.

当μ1=δ1σ+y0时，模糊质量损益的“模糊田口指数”为

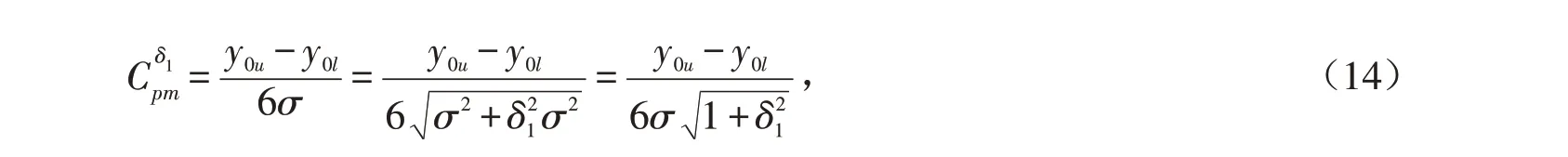
其中，y0u为产品规格上限，y0l为产品规格下限；σ′2=E[(Y-Y0)2]表示产品特征值y偏离目标值y0的方差的期望，有

而过程未发生偏移，即μ=y0，δ=0 时，模糊质量损益的期望为E[L1(0)]，“模糊田口指数”为

表1 、、与δ1 关系表Tab.1 Relationships among ，and δ1

表1 、、与δ1 关系表Tab.1 Relationships among ，and δ1

R(1)k δ1 R(1)L R(1)p R(1)k δ1 R(1)L R(1)p 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2-0.025 19-0.020 16-0.015 12-0.010 08-0.005 04 0 0.005 042 0.010 083 1.161 064 5 1.166 416 2 1.171 822 9 1.177 285 4 1.182 804 0 1.188 381 5 1.194 016 9 1.199 711 7 0.999 683 0.999 797 0.999 886 0.999 949 0.999 987 1 0.999 987 0.999 949 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 0.015 122 0.020 159 0.025 194 0.030 224 0.035 251 0.040 272 0.045 287 0.050 295 1.205 466 8 1.211 283 3 1.217 162 0 1.223 104 0 1.229 110 3 1.235 182 0 1.241 319 9 1.247 525 4 0.999 885 0.999 796 0.999 683 0.999 544 0.999 379 0.999 190 0.998 976 0.998 738

2.2 二次非对称模糊质量损益函数过程均值设计

讨论过前两种情况后，以同样的方法对二次非对称模糊质量损益函数进行讨论，假设产品的质量特性值y服从正态分布N(μ,σ2)，根据模糊质量损益函数定义，在生产的工序过程未调整之前时，其输出均值μ 与目标值y0一致，将函数定义为两侧参数不同的二次函数的情况，则关于模糊质量特征y的模糊质量损益函数为

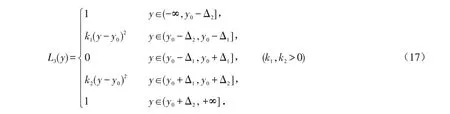
其函数图像为图6所示.

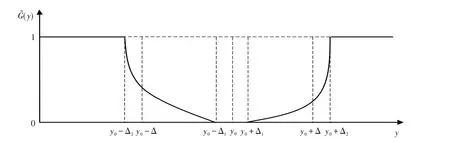
图6 二次非对称模糊质量损益函数图像Fig.6 Quadratic asymmetric fuzzy quality gain-loss function image

同样的，对式（17）的函数求期望得出

简化后令

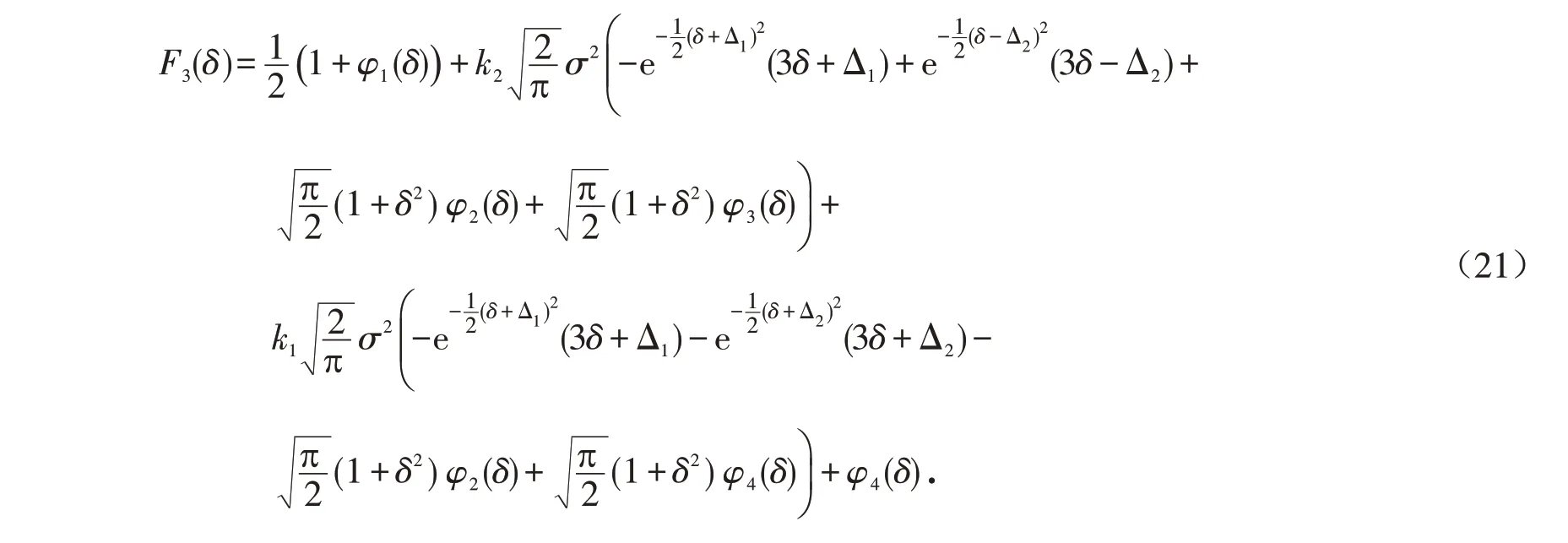
根据计算得知，E[L3(δ)]=F3(δ)，则F3(δ)是E[L3(δ)]归类化简后的函数，两者实质是同一个函数，且具有相同的极值点. 求F3(δ)关于δ 的一阶微分，并令其等于零，可得出F3(δ)的所有极值点.

由于E[L3(δ)]与F3(δ)有相同的极值点δ3，再由δ=得出μ3=δ3σ+y0，即μ3为模糊最优均值.

当μ3=δ3σ+y0时，模糊质量损益的“田口指数”为

其中，y0u为产品规格上限，y0l为产品规格下限；σ′2=E[(Y-Y0)2]表示产品特征值Y偏离目标值Y0的方差的期望，有

而过程未发生偏移，即μ=y0，δ=0 时，模糊质量损益的期望为E[L3(0)]，则“模糊田口指数”为

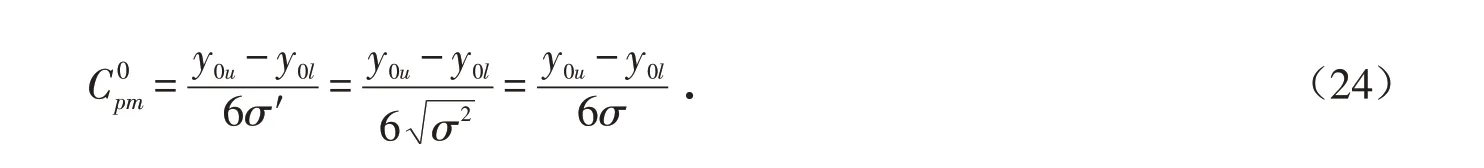
表2 、、与δ3 关系表Tab.2 Relationship among ，and δ3

表2 、、与δ3 关系表Tab.2 Relationship among ，and δ3

R(3)k δ3 R(3)L R(3)p R(3)k δ3 R(3)L R(3)p 0 0.3 0.7 1 1.4 1.8 2.3 2.7 0.001 416 5 0.000 986 1 0.000 419 5 0-0.000 552 2-0.001 096 0-0.001 766 2-0.002 293 3 1.188 365 1 1.188 361 0 1.188 355 7 1.188 351 8 1.188 346 7 1.188 341 6 1.188 335 3 1.188 330 4 0.999 998 9 0.999 999 5 0.999 999 9 1 0.999 999 8 0.999 999 3 0.999 998 4 0.999 997 3 3.1 3.5 3.9 4.3 4.7 5.1 5.5-0.002 813 1-0.003 325 6-0.003 831 0-0.004 329 4-0.004 821 0-0.005 305 9-0.005 784 3 1.188 325 6 1.188 320 8 1.188 316 0 1.188 311 4 1.188 306 8 1.188 302 2 1.188 297 8 0.999 996 0 0.999 994 4 0.999 992 6 0.999 990 6 0.999 988 3 0.999 985 9 0.999 983 2

3 实例分析

丹江口大坝加高工程原材料、中间产品、设备构配件质量的检测情况中，对中间产品质量情况的混凝土拌和物性能进行了抽检. 右岸标段施工单位在军营拌和楼出机口抽检混凝土含气量5265次，合格率95.0%～100%；抽查混凝土坍落度5611 次，合格率96.6%～100%；抽查混凝土出机口温度8097 次，合格率94.0%～100%. 左岸标段施工单位在小胡家岭拌和物出机口抽检混凝土含气量8299次，合格率99.6%～99.9%；抽查混凝土坍落度15 832次，合格率97.8%～100%；抽查混凝土出机口温度20 754次，合格率96.4%～99.5%. 监理单位抽查检测混凝土拌和物含气量4175 次，合格率89.6%～100%；抽查检测混凝土拌和物坍落度（扩散度）4317 次，合格率90.6%～100%；抽查检测混凝土拌和物温度4044 次，合格率75.0%～100%. 混凝土拌和物质量符合设计及规范要求.

根据工程实际及设计要求可知，混凝土拌和物含气量质量特征指标服从正态分布为N(μ,0.52)，混凝土拌和物含气量为望目特征，其目标值为5%. 由于在实际施工过程中，对指标的界定具有一定模糊性，模糊质量损益函数为了更好地反映实际情况，我们将二次非对称模糊质量损益函数的参数定为k1=0.6，k2=0.1，Δ=0.4，Δ1=0.02，Δ2=0.43. 则模糊质量损益函数为

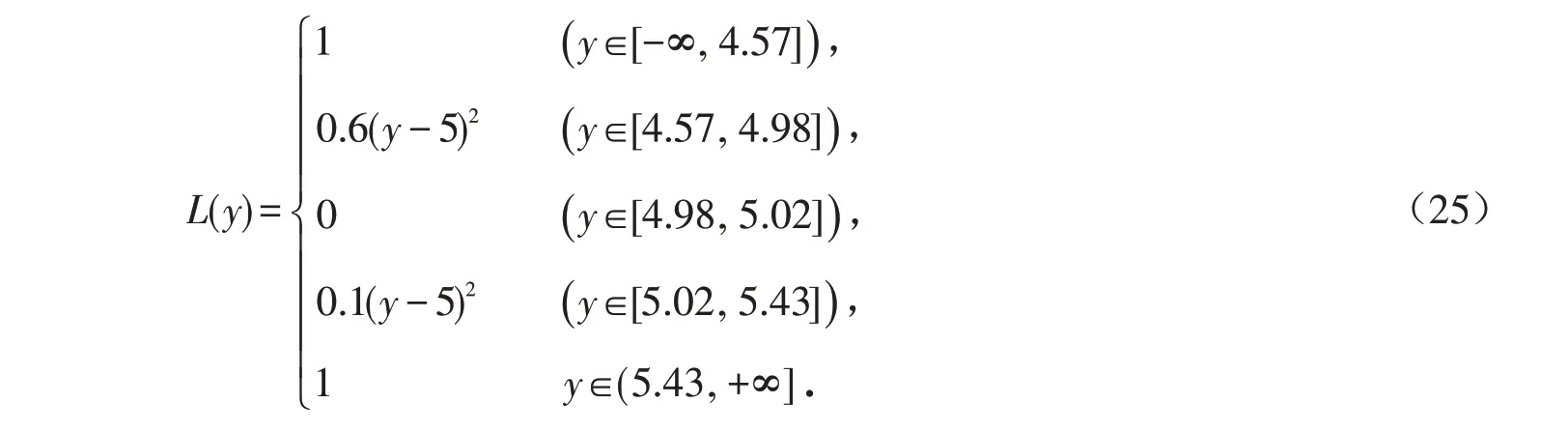
根据二次非对称模糊质量损益函数的讨论可知

由Rk=k1/k2=6 可得，Rk=6 时，δ=-0.032 753. 则最优模糊过程均值设计为：μ=5+0.5×（-0.032 753）=4.983 623，此时模糊质量损益率为1.495 517 5，模糊过程有效偏移率为0.999 46. 丹江口大坝加高工程混凝土拌和物含气量质量控制研究中，建立了二次非对称模糊质量损益函数，模糊过程均值μ=4.983 623小于目标值y0=5，此时为最优模糊过程均值，且得出模糊非对称比率越大，调整的程度越小，模糊质量损失率也越小，而模糊过程有效偏移率呈现增大后减小的趋势.

4 结论

由于产品质量特性目标值具有模糊性，应用模糊理论对质量损益函数模型进行拓展，提出了模糊质量损益函数的概念，并由此建立了相应的模糊质量损益模型. 在产品的质量特征服从正态分布，模糊质量损益非对称的情况下，进行了模糊过程均值的优化. 研究了两种典型非对称模糊质量损益的模糊过程均值设计问题，根据提出的模糊有效偏移率、模糊对称比率以及模糊质量损益率的概念，分析探讨了这三者之间的变化趋势及规律.