一种分布式多传感器信息融合方法*

彭圆红,吴晓锋

(闽南师范大学数学与统计学院,福建 漳州 363000)

目标状态融合是信息融合的重要组成部分,因其在军事和民用领域的大量应用而受到广泛关注。

目前,关于目标状态跟踪融合系统,人们已经提出了多种融合结构,例如:集中式[1-4]、分布式[4-7]、混合式[4，8]、多级式[4，9]等。这些结构中都含有一个融合中心,该融合中心将来自不同区域的多个传感器的信息进行融合,以生成新的目标点迹跟踪,并发送新的目标跟踪状态到每个传感器,使得传感器间获得一致的目标信息,实现态势共享。显然,具有融合中心的信息融合结构存在着安全性能低、通信资源消耗大等缺陷[1，3]。因此,如何去除融合中心,建立具有多地并行融合特征的分布式信息融合结构,是一个亟待研究的问题。

对于目标状态跟踪融合算法的研究,分布式卡尔曼滤波是一种具有多地并行融合特征的分布式信息融合算法,已成为近年来的一个研究热点[10-16]。在这种分布式融合方案中,部署在每个传感器中的卡尔曼滤波器接收来自其他传感器的目标点迹信息,并利用这些信息估计目标的跟踪点。然而,分布式卡尔曼滤波并没有解决传感器之间的信息一致性问题。

为此,本文提出了一种新的多传感器分布式信息融合方案。在该方案中,每个传感器只与部分传感器(称为“邻居”)交换目标点迹信息,并通过本地融合处理器对获得的信息进行综合,形成去中心化、多地并行融合的方案。借助舆情动力学[17-19]和信息一致性[20-22]理论设计了一种分布式融合算法,可以使每个传感器在一定的网络拓扑条件下通过运行该融合算法获得一致的目标点迹信息。

1 一种新的分布式信息融合结构

为了描述的方便,对传感器网络的有关概念、数学符号等定义描述如下。

考虑单个目标的位置融合问题,假设有n个传感器组成的传感器集合,记为V={1,2,…,n},其中，每个传感器至少与另外一个传感器进行有向信息传递,从而构成一个有向传感器网络。对于任意的传感器i,j∈V,若传感器i可以收到来自传感器j的信息,那么就存在一条从传感器j到传感器i的有向边,反之亦然。采用图G=(V,E)来表示传感器网络的拓扑结构,其中，V是传感器集合,E是有向边集合。从传感器j到传感器i的有向边,记作(i,j)∈E,其中，传感器j称为传感器i的“送信”邻居,传感器i称为传感器j的“收信”邻居。传感器i的“送信”邻居与“收信”邻居统称为传感器i的邻居。

“从传感器i到传感器j之间存在一条长度为k的有向路径”是指存在一组有序的传感器i0,…,ik∈V,其中i0=i,ik=j,并且对任意的s=1,2,…,k,相邻两个传感器通过有向边(is,is-1)连接。从传感器到自身的有向路径(长度为1)称为该传感器节点的自环。如果一个传感器没有“送信”邻居,并且从该传感器出发到其他任意一个传感器都存在一条有向路径,那么称它为“根”传感器。若有向传感器网络G中的任意两个传感器之间存在一条有向路径,那么称该网络是强连通的。一棵有向树是指含有一个根传感器的有向网络,且除根传感器之外,其余传感器仅有一个“送信”邻居。如果存在一棵有向树覆盖了传感器网络中的所有传感器,则称该传感器网络含有一棵有向生成树。

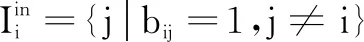
现有的基于融合中心的分布式信息融合结构由图1所示[4]。在这种融合结构中,由每个传感器对目标产生多目标跟踪,然后把多目标跟踪信息传送至融合中心,融合中心根据各传感器的目标跟踪信息完成数据对正、航迹关联和航迹融合,形成目标状态信息(如点迹)的全局估计,并将融合后的目标状态信息反馈给各传感器,使得每个传感器对目标状态达成共识。

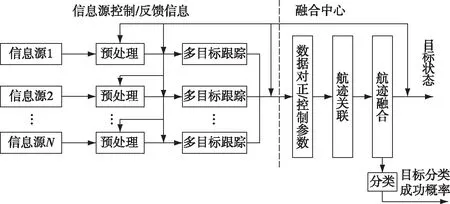
图1 基于融合中心的分布式融合结构

然而,这种基于融合中心的融合结构也存在一些缺陷。首先,信息融合的任务集中在融合中心执行,这意味着融合中心一旦发生设备故障或被恶意攻击,整个传感器网络的信息融合功能将下降甚至瘫痪。因此,为了安全,融合中心可能需要部署在远离前端传感器的后方位置上,这时就要求传感器网络具有较强的通信能力,如较大的通信距离和带宽等,特别是对于无线和移动传感器网络而言。

为了克服上述问题提出一种新的信息融合结构,如图2和图3所示。在新的融合结构中,每个传感器(平台)都含有两个处理器:数据处理器和融合处理器。数据处理器用于对传感器检测到的目标信息进行处理,产生本地的目标点迹,并将本地目标点迹发送到本地融合处理器。融合处理器用于接收本地数据处理器的目标点迹信息和“送信”邻居的融合处理器产生的目标点迹信息,然后对这些目标信息进行时空校正、数据关联和融合,生成新的目标点迹信息,并将更新的目标点迹信息发送给“收信”邻居,如图2所示。

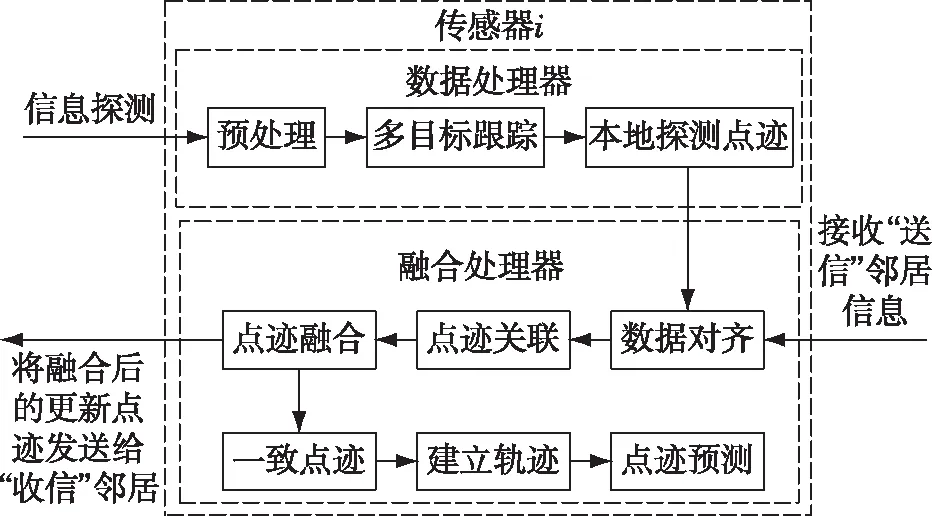
图2 传感器i的内部处理器

在这里,每个传感器不需要与其他所有传感器都能进行通信,而只需与其通信范围内的部分传感器(称为“邻居”)进行有向信息交换,即每个传感器仅需将本地融合后的目标点迹信息传递给“收信”邻居,同时接收“送信”邻居发送的融合目标点迹信息。我们希望,在只得到来自“送信”邻居的目标点迹信息情况下,每个传感器的融合处理器通过一定的融合算法,能自主地修改目标点迹数据,并最终达成对目标点迹的一致判断。由此形成了一种由分布在各传感器中的多个融合处理器并行融合的分布式目标点迹信息融合结构,如图3所示。

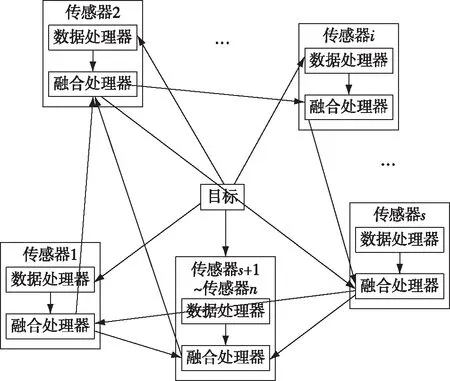
图3 分布式信息融合结构

在新的分布式传感器信息融合结构中,每个传感器的数据处理器可能获得全部或部分目标的点迹信息。此外也允许存在一些传感器,它们没有检测到任何目标,称之为“盲”传感器,如图3中的传感器s。在这里,我们需要解决的问题是:如何设计共用于每个传感器的融合算法,使得每个传感器的融合处理器运行该融合算法时,可以在一定的传感器网络拓扑下,得到一致的目标点迹信息,即使有“盲”传感器存在。

与基于融合中心的信息融合结构相比,新的分布式信息融合结构具有许多优点。首先,在新的信息融合结构中,分布在各传感器中可并行处理的多个融合处理器取代了传统的单一融合中心的融合方式,这意味着即使某些传感器的融合处理器出现故障或失效,也不会导致整个传感器网络信息融合的失败,提高了传感器网络的鲁棒性。其次,在新的信息融合结构的运行过程中,每个传感器只需与其邻居进行有向信息传递,简化了传感器网络的拓扑结构。最后,在新的信息融合结构中,某个传感器只要不成为“信息孤岛”,即使它与一些传感器的通信连接中断,也不会影响该传感器与其他传感器的目标点迹融合,并可以共享传感器网络的信息融合结果。而在基于融合中心的信息融合结构中,与融合中心失去连接的传感器将无法参与信息融合,也无法共享信息融合结果。

2 融合算法

假设传感器网络的目标跟踪过程是一个以t0时刻为始点的序贯相接的有界时间域序列Tm=[tm,tm+1),m=0,1,2,…。在每个有界时间域Tm=[tm,tm+1)内,每个传感器i对本地数据处理器检测得到的目标点迹信息zi(m)和来自“送信”邻居的目标点迹信息按照图3所示的分布式融合过程进行融合,从而获得一个目标点迹在Tm时的(一致)融合结果。

考虑在时域Tm内,将该时域划分为另一个序贯的有界时域序列qk=[τk,τk+1),k=0,1,2…。在每个有界时域qk内,每个传感器与“送信”或“接信”邻居之间进行一次信息传递,并按照一定的融合算法综合处理来自“送信”邻居和自身的目标点迹信息,产生一次目标点迹信息的更新。假设不存在传感器网络时延、通信噪声、信息丢失等不确定性因素。

针对上述问题,传感器i用于目标点迹信息更新的融合函数给定如下:

xi(k+1)=fi(xi(k),xi1(k),…,xil(k))

(1)

基于融合函数(1),每个传感器将其数据处理器获得的目标一维点迹信息zi(m)作为融合算法的初值, 如果传感器i在Tm内是“盲”传感器,则令xi(0)=∞，再将融合算法每次更新后的目标点迹信息传递给“收信”邻居,同时接收“送信”邻居更新后的目标点迹信息进行下一次综合和更新。本文的工作是设计合适的融合函数,建立相应的融合算法,使得在一定的传感器网络拓扑条件下,即使传感器网络中存在“盲”传感器，对于各传感器的任意初始融合状态xi(0)都有

(2)

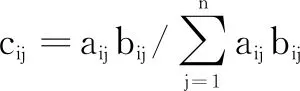
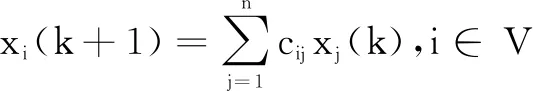
(3)

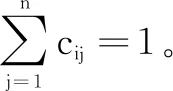
函数模型(3)可以集成为如下矩阵形式:

x(k+1)=Cx(k),k=0,1,2,…

(4)

其中，x(k)=(x1(k),x2(k),…,xn(k))T,C=(cij)∈Rn×n称为传感器网络G的相对信任度矩阵。显然,矩阵C是一个行随机矩阵。考虑传感器网络拓扑与传感器之间的信任度均为时不变的情况,因此矩阵C也是时不变的。由于信任度矩阵A>0(不含零元素),因此，相对信任度矩阵C对应的网络拓扑结构与传感器网络拓扑结构相同。

函数模型(4)可以进一步推导为

x(k+1)=Ck+1x(0),k=0,1,2,…

(5)

其中，x(0)=(xi(0),x2(0),…,xn(0))T为融合初值,由各传感器探测得到。根据融合函数(3),传感器i的离散时间融合算法可表述如下:

步骤1.k=0时,传感器i的数据处理器检测得到目标点迹信息xi(0),并将该信息发送到其融合处理器;

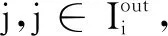
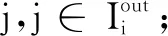
步骤5. 如果对任意i,j∈V,有xi(k+1)=xj(k+1),融合结束;否则k=k+1,返回到第3步。

命题. 对于任意初始值x(0),每个传感器通过运行融合算法(3)达到(2)意义下的一致融合,当且仅当传感器网络含有一棵有向生成树。进一步地,如果该传感器网络含有一棵有向生成树,则有

(6)

∀i,j∈V

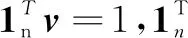
由上述命题可以得到如下推论。

推论. 如果传感器网络有且仅有一棵有向生成树,那么对于任意初始值x(0),每个传感器通过运行融合算法(3)可以达到(2)意义下的一致融合,并且一致融合结果为有向生成树根传感器的数据处理器检测得到的目标点迹信息。

与分布式卡尔曼滤波算法[12-16]相比,本文提出的算法并没有对目标的轨迹进行预测,而是对各传感器的数据处理器检测得到的目标实时点迹信息进行分布式融合,使各传感器获得一致的实时目标点迹信息。

3 实例分析

在给定的时域Tm内,考虑由6个传感器构成的一个传感器网络。假设传感器6的数据处理器没有检测到目标而成为一个“盲”传感器,因此,它不会发送任何信息给其他传感器。在融合初始(k=0),设计其传感器网络如图4所示;当融合时间k≥1时,其传感器网络如图5所示。显然,图5的传感器网络是强连通的。

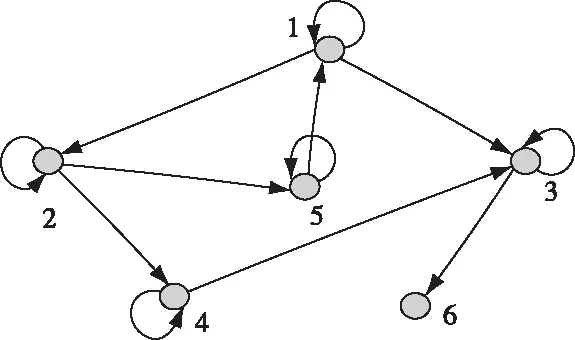
图4 传感器网络1(k=0)

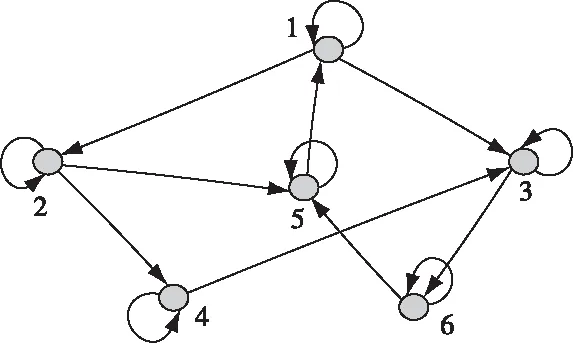
图5 传感器网络2(k≥1)

再假设传感器集合V={1,2,…,6}中的传感器探测性能依次降低,并且传感器总是对探测性能高的其他传感器给予较高的信任度。因此,设定传感器网络的信任度矩阵A为

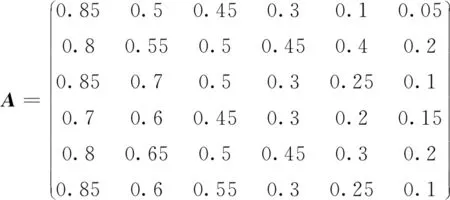
(7)

根据图4所示的传感器网络结构,可以得到该传感器网络的初始邻接矩阵为

(8)

由信任度矩阵A和初始邻接矩阵B0可得到初始相对信任度矩阵C0如下:

(9)

再根据图5所示的强连通传感器网络结构,可以得到该传感器网络的邻接矩阵为

(10)

由信任度矩阵A以及上述邻接矩阵Bk≥1可得到相对信任度矩阵Ck≥1如下:

(11)

在此情况下,可将融合函数(4)改写为

x(1)=C0x(0)

x(k+1)=Ck≥1x(k),k=1,2,…

设各传感器的数据处理器获得的目标点迹信息为x(0)=(168,156,145,174,158,∞)T。根据上述算法,用Matlab软件可得到传感器网络分布式融合过程的仿真结果,如图6所示。

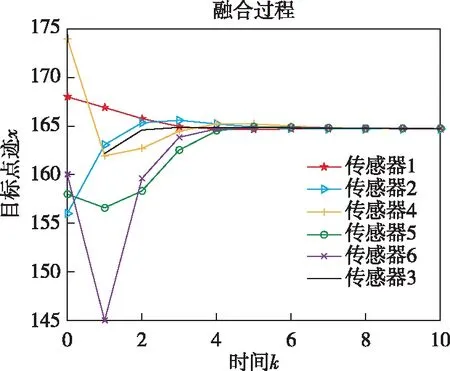
图6 含“盲”传感器网络的分布式融合过程

从图6可以看出,尽管传感器6是“盲”传感器,但由于传感器网络(图5所示)是强联通的,传感器6最终也能够通过分布式融合算法与其他传感器达成一致融合结果。

观察上述传感器网络的一致融合结果(164.73),可以发现它更接近传感器1的数据处理器检测到的目标点迹信息。由此可推测,探测性能高的传感器对一致融合结果的影响更大,传感器网络的融合结果更接近于探测性能高的传感器检测得到的目标点迹。

4 结束语

多传感器信息融合如何去中心化是目前十分受关注的科学问题。本文提出了一种基于多地并行融合、去中心化的分布式多传感器信息融合方案,在每个传感器上配置一个融合处理器,通过传感器间的信息通信以及融合处理器解决目标状态(位置)的融合。基于新的融合结构提出了一种离散时间融合算法,通过运行该融合算法各传感器可以达到对目标状态(点迹)信息的一致融合,即使存在“盲”传感器，还给出了该融合算法的一致性条件,分析了一致融合结果的收敛情况。最后,实例仿真也验证了所提出的融合算法的有效性和有关一致性理论的正确性。