用于蚯蚓分选的直线振动筛研究与试验

2020-10-19吴祥臻赵洪新

农机化研究 2020年4期

关键词：激振力筛网振动筛

吴祥臻,贺磊,赵洪新

(山东理工大学,山东淄博 255000)

0 引言

蚯蚓的生长周期较短,养殖模式以大田养殖为主,采用的分选方法大多是人工分选,分选过程需要耗费大量人力资源,限制了蚯蚓养殖的规模。为此,本文从理论分析和样机试验两个角度对直线振动筛进行了研究分析,旨在为蚯蚓分选所采用的直线振动筛提供设计依据。

1 直线振动筛理论分析

1.1 工作原理

图1为用于蚯蚓分选的直线振动筛三维模型。

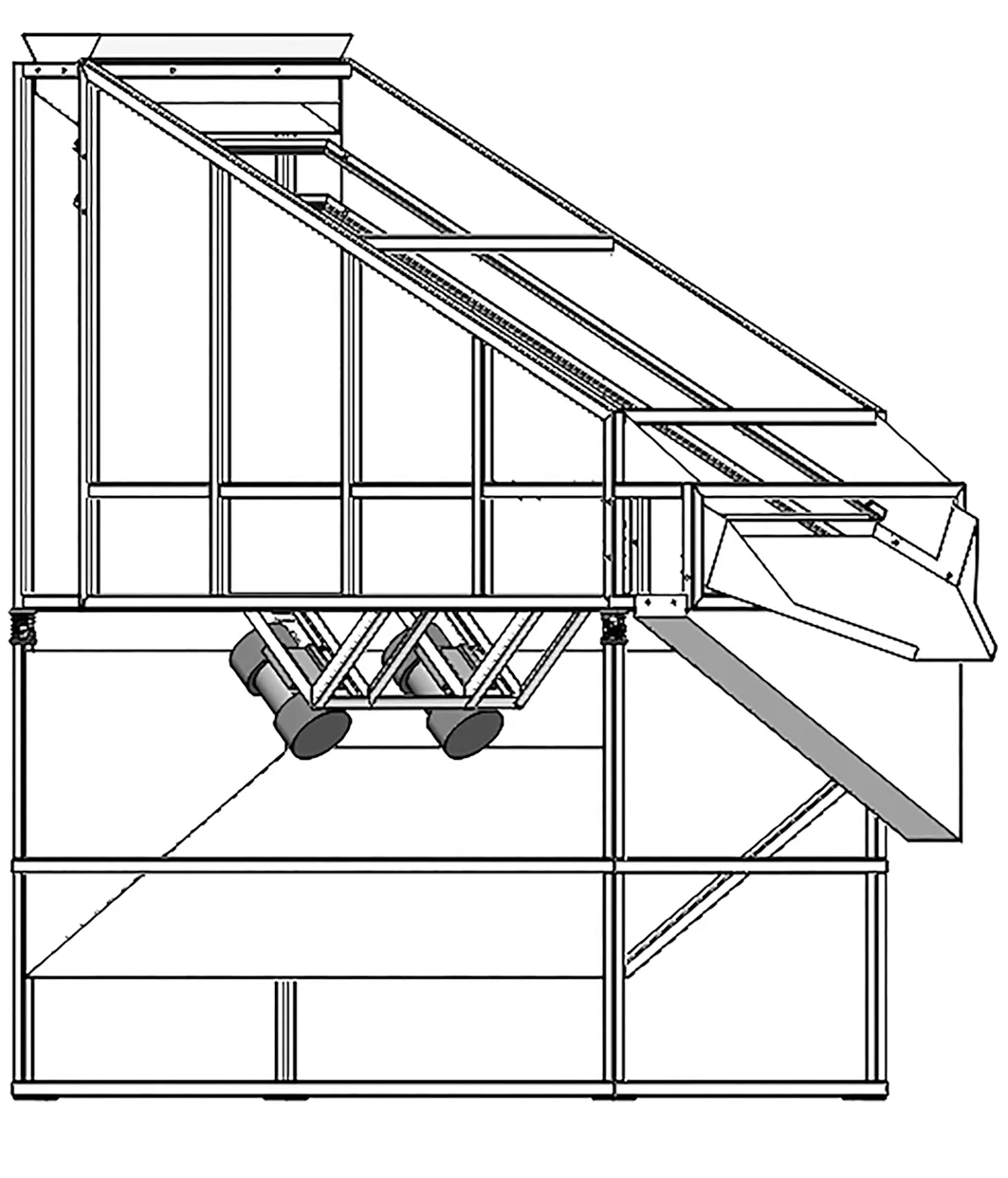
图1 直线振动筛三维模型Fig.1 3D model of linear vibrating screen

图1中,振动的激振力由两同步异向旋转的双不平衡振动电机提供,振动电机的安装呈一定角度;两台振动电机同步反向旋转,电机的偏心块旋转产生的惯性离心力在X轴上的分力相互抵消,沿Y轴的分力相互叠加,电机偏心块运动到图2(a)、(c)位置时,两振动电机提供的激振力最大;电机偏心块运动到图2(b)、(d)位置时,两振动电机提供的激振力最小。

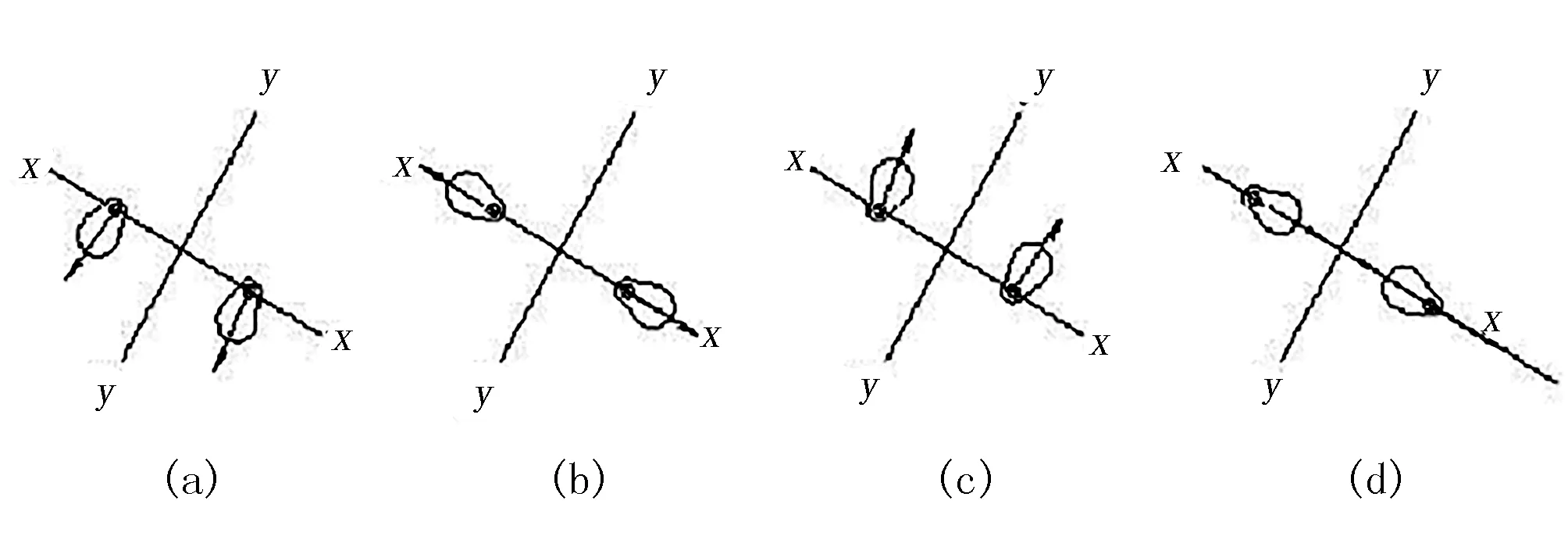
图2 偏心块运动状态图Fig.2 Motion diagram of eccentric block

由以上分析可得直线振动筛的运动方程为

S=λsinωt

(1)

其中,S为直线振动筛在振动方向上的位移;λ为直线振动筛的振幅;ω为振动电机的角速度;t为振动电机运转时间。

振动电机激振力的方向与筛面的方向夹角为α,设平行筛面方向为X轴,垂直筛面方向为Y轴,直线振动筛在振动方向上的位移可在X轴、Y轴上进行分解,得到延坐标轴的分位移x、y,分别求x、y的1阶、2阶导数,可以得到直线振动筛在X轴、Y轴的速度、加速度方程,即

(2)

其中,α为振动电机激振力的方向与筛面的方向夹角。

1.2 直线振动筛力学模型

直线振动筛是个复杂的机械系统,机械系统的运动分析通常比较困难,所以需要对机械系统进行简化处理。直线振动筛工作时的运动形式是受迫振动,系统在激振力的作用下做周期性运动,对系统进行简化处理。简化原则如下:

1)质量集中原则。直线振动筛箱体质量较大,忽略其弹性变形,简化为质量为M的刚体。

2)刚度集中原则。直线振动筛由4只弹簧支撑,在刚度分析时忽略弹簧质量,弹簧的刚度集中到系统整体的刚度进行分析。

3)阻尼集中原则。机械系统的存在的很多种阻尼形式,且多为非线性阻尼。为了便于计算,将系统阻尼简化为线性阻尼进行力学分析。

4)振动集中原则。实际工作中,直线振动筛并不是只做受迫振动,机械系统中存在其他小位移振动,在进行力学分析时忽略其他方向的小位移振动,只考虑y轴方向上的机械系统的受迫振动。

综合以上简化原则,建立直线振动筛的力学模型,如图3所示。

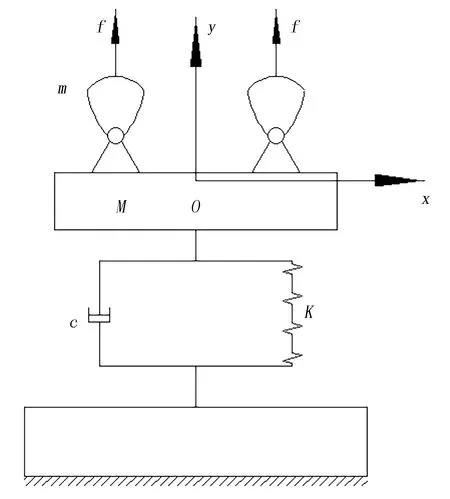
图3 直线振动筛力学模型Fig.3 Mechanical model of linear vibrating screen

由图3可知:作用于机械系统的外力主要为激振力f、弹簧弹力及系统的阻尼力。激振力f=f0sinωt,f0为激振力的幅值。根据达朗贝尔原理,作用在系统上的主动力和系统的惯性力之和为零,则机械系统的运动学方程为

(3)

其中,M为直线振动筛上箱体质量;m为振动电机偏心块质量;c为系统阻尼系数。

2 直线振动筛箱体动力学分析

直线振动筛的箱体在交变载荷作用下,容易发生侧板的变形、开裂,以及横梁的断裂等现象,严重影响直线振动筛的使用寿命。当箱体产生共振现象时,系统振幅显著增大,箱体受到的动应力显著提高,极易引起箱体的破坏性变形。为了提高直线振动筛的使用寿命,需要进行系统的模态分析,避免共振现象发生。

将UG10.0中建立的直线振动筛箱体模型进行简化,忽略定位孔、工艺孔等细节特征,导入Workbench12.0中。为了简化运算,将箱体看成是一个整体,对整体进行划分网格,模态分析不需要施加外载荷,设置箱体底面弹簧接触约束。结构振动中,高阶模态能量所占的比重很低,所以在进行模态分析时只计算前15阶固有频率,如表1所示。

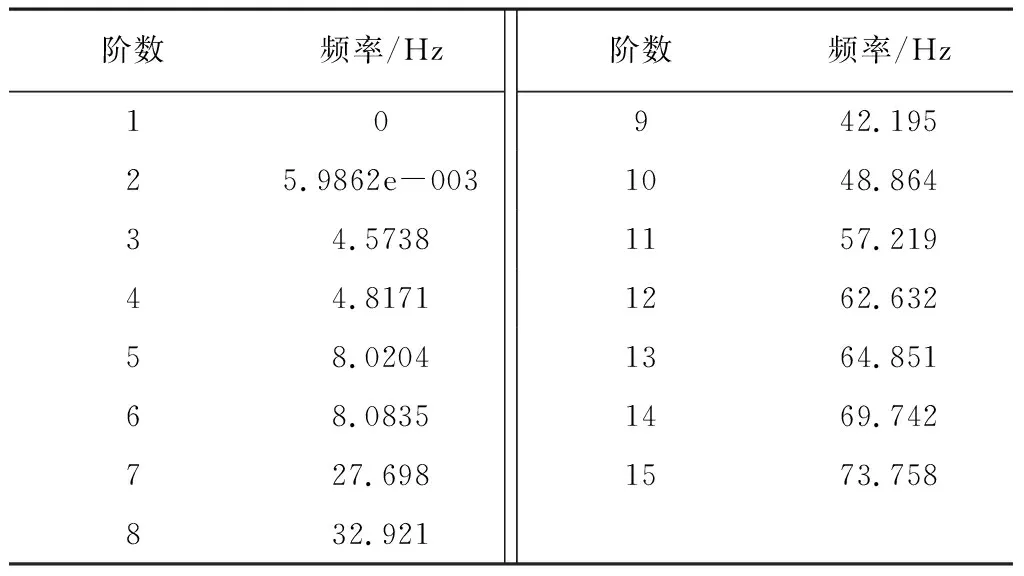
表1 筛体前15阶固有频率Table 1 The first 15 natural frequencies of the sieve body

前期工作中通过计算选择1000r/min的yzs-5-6型振动电机,直线振动筛的工作频率为16.67Hz。为了防止出现共振现象,工作频率不得落入各阶固有频率的半功率带宽内。

直线振动筛的工作频率避开了固有频率,因此不会发生共振,符合设计要求。直线振动筛前10阶模态振型图如图4所示。

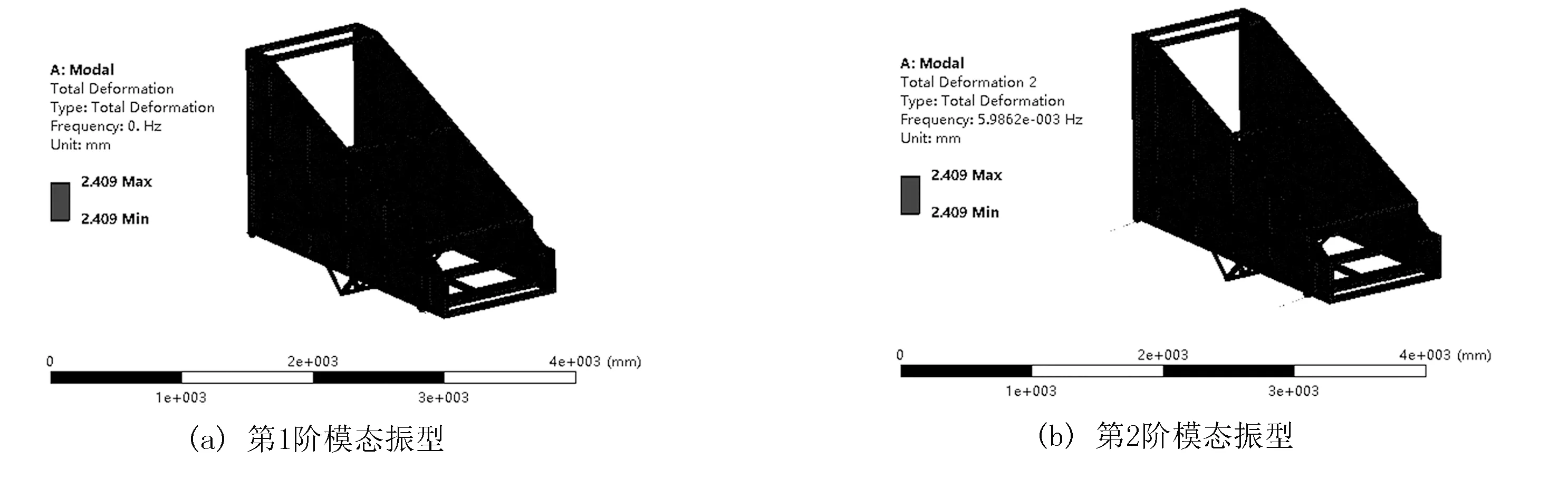
图4 直线振动筛前10阶模态振型图Fig.4 Front ten mode vibration pattern of linear vibrating screen

3 直线振动筛样机试验

3.1 试验样机

前文对振动筛的工作原理及三维模型设计的合理性进行了分析,振动筛的分选效果要通过样机(见图5)试验进行验证。直线振动筛的分选效果直接受振动参数影响,为了方便试验,减少样机设计成本,所以在进行样机设计时将重要设计参数设计为可调,参数包括激振力和筛网倾角。

图5 直线振动筛样机图Fig.5 Prototype of linear vibrating screen

1)激振力。激振力影响了振动筛正常工作时相对平衡位置的最大位移,不同的筛分物最佳筛分激振力也不同,本节将用试验的方法探讨最佳激振力。

2)筛网倾角。筛网与水平面的夹角为筛网夹角,其大小直接影响筛分效率和处理速度。夹角越大,越有利于物料做斜抛运动,物料在筛网上的停留时间就越短,物料的运动速度越快,振动筛的处理速度越快。本节将在设计合理角度的范围内进行试验,选择分选的最佳角度。

3.2 试验设计

为了研究振动参数之间的相互作用,找到整个区域上参数组合值的最优解。对振动参数取不同的水平值,进行全因子样机试验,得出最佳筛分参数设计。

试验考察两个筛分参数,分别为A(激振力)、B(筛网倾角)。前期工作中,已初步确定各振动参数的调节范围,如表2所示。试验目的是为了找到参数组合中的最优解,使振动筛达到最佳分选效果,即筛分物中蚓粪充分过筛,蚯蚓尽量少地过筛。试验结果如表3所示。

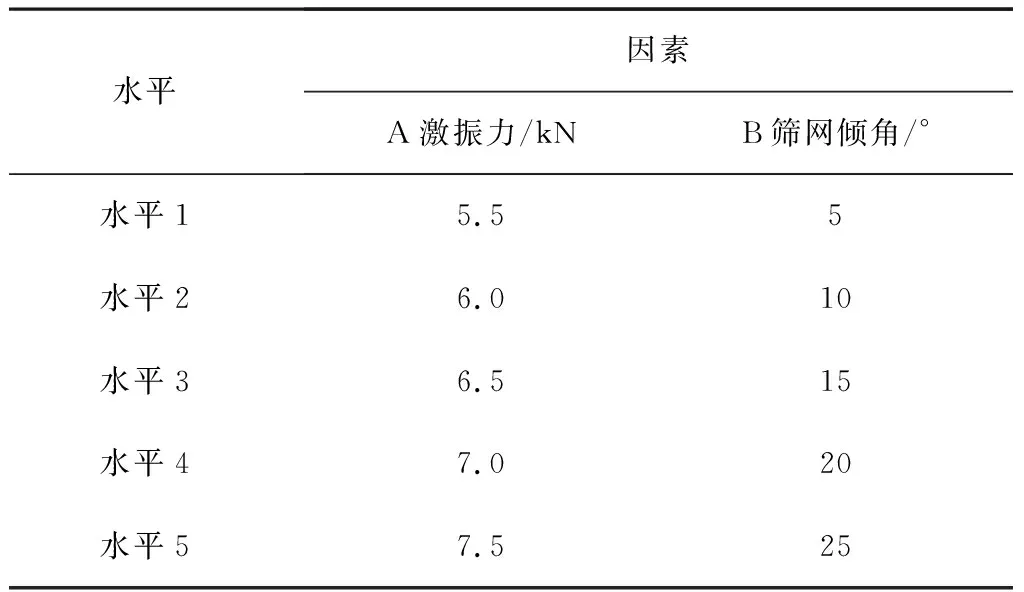
表2 试验因素设计Table 2 Design of test factors

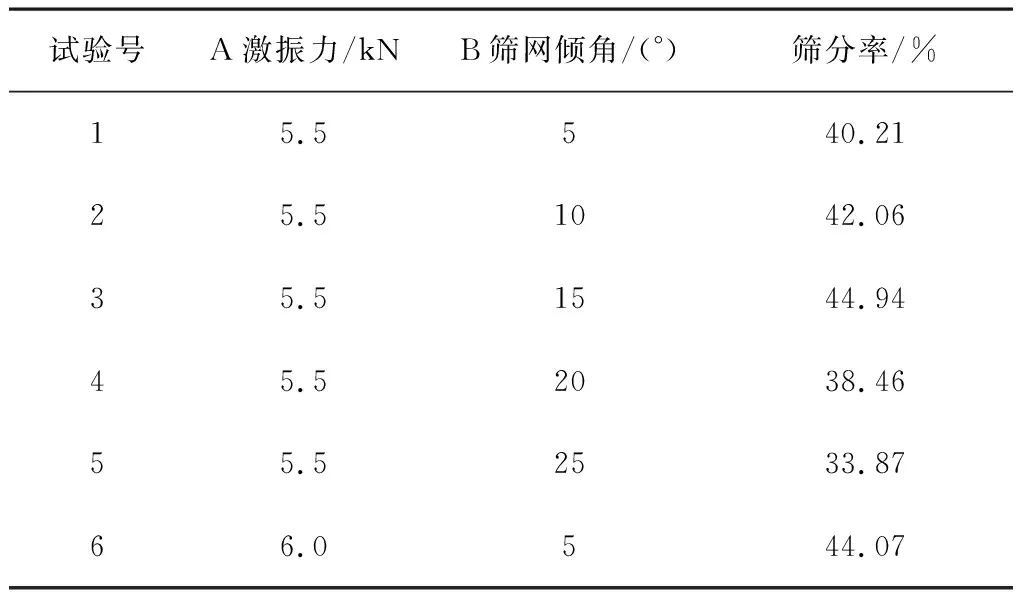
表3 筛分试验结果Table 3 Results of screening test

3.3 结果后处理

1)极差分析。对试验结果进行极差分析,可以直观地反映激振力和筛网倾角对筛分率的影响,如表4所示。由表4可知,RB>RA。这说明,A、B因素对于筛分率影响的重要程度依次是筛网倾角、激振力。对于A因素来说,不同水平下的筛分率极差为k3>k4>k2>k5>k1;对于B因素,不同水平下的筛分率极差为k2>k3>k1>k4>k5。因此,振动式分选装置取得最大筛分率时的筛分参数组合为A3B2,即激振力为6.5kN、筛网倾角为10°。对应试验表中12号试验,此时筛分率为60.82%。

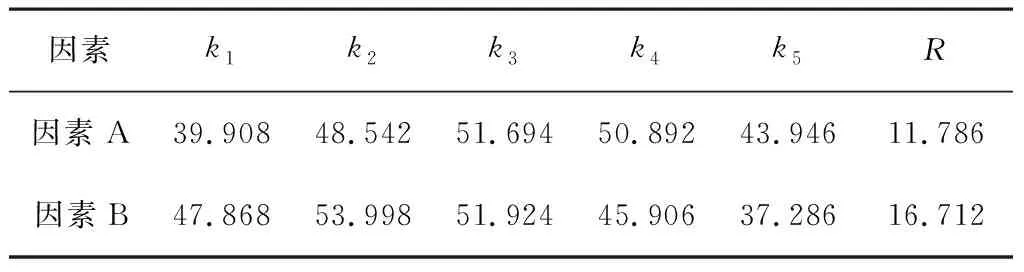
表4 筛分率极差分析表Table 4 Screening rate range analysis table

2)趋势分析。因素-筛分率趋势图如图6所示。由图6可知,筛分率随激振力和筛网倾角的变化而不断变化。在筛分过程中,随着激振力的增大,筛分率的变化趋势是先增加后降低。当激振力较低时,物料的振幅较低,使得物料分层效果较差。同时,物料在筛面上的运动速度较低,造成物料堆积,料层厚度较高,使得筛分率较低。当激振力过大时,物料在筛面上的运动过快,物料在筛面上的停留时间较短,物料的筛分率低。随着筛网倾角的增大,筛分率的变化趋势是先增加后降低,筛网倾角过小时,增大筛网倾角提高了物料在筛面上的运动速度。当筛网倾角过大时,一方面使得物料在筛面上的运动速度过高,使得物料筛分不充分;另一方面筛网的有效过筛面积降低,颗粒过筛概率的降低使物料的筛分率降低。

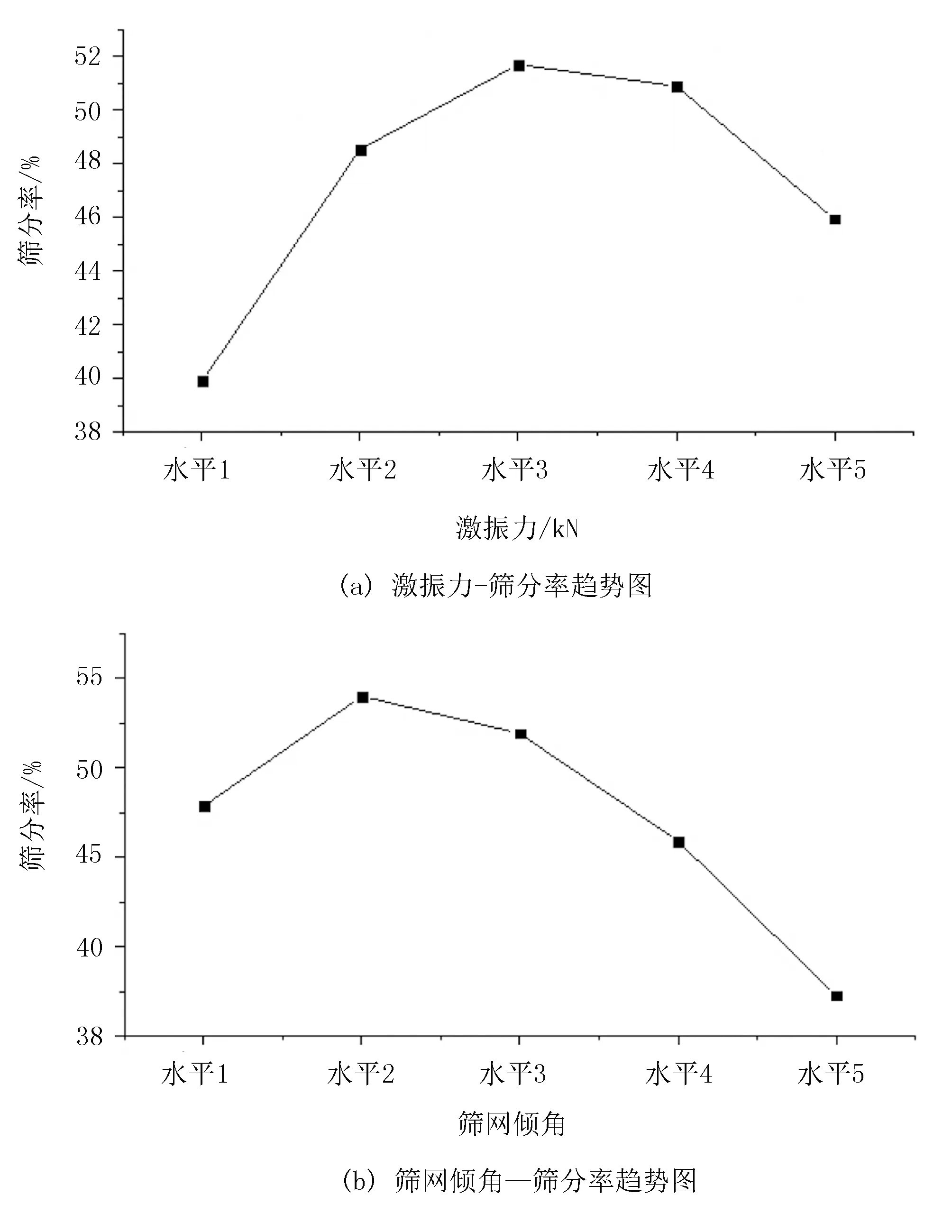
图6 因素-筛分率趋势图Fig.6 Factors - screening rate trend chart

3.4 最优筛分参数确定

由试验结果可知:筛分过程中,蚯蚓的过筛损失量占每箱培养基中蚯蚓的质量比重较低,损失量在可接受范围内,可以证明在筛网孔径取5mm在进行蚯蚓分选时是合理的。以蚓粪的筛分率为指标,当蚓粪的过筛率取最大值时,激振力与筛网倾角的最佳参数设计分别为6.5kN、10°,对应试验表中12号试验,此时筛分率为60.82%。