跨层穿梭车双提升机系统料箱拣选任务调度

于巧玉，吴耀华，王艳艳

山东大学 控制科学与工程学院，济南 250061

1 引言

随着近年来电子商务行业的快速稳健发展，大量的网络购物订单涌入到企业的仓库管理系统中，同时顾客对订单履行的时效也提出了更高的要求。如何快速、准确地满足订单的拣选出库要求，是电商企业面对海量订单首先要解决的问题。跨层穿梭车双提升机系统（tier-totier shuttle-based storage and retrieval system with double lifts）是一种结合电商企业仓储拣选特点，基于“货到人”（Part-to-Picker）理念而设计，集存储和拣选于一体的现代化仓储系统[1]。该系统通过多层多巷道立体货架实现密集存储，以料箱为存储单元，穿梭车和提升机组合代替传统自动化立体仓库中的堆垛机，分别完成料箱出入库的水平搬运和垂直搬运，通过自动化智能设备和计算机管理控制系统之间的双向通信，将料箱输送至拣选台，待拣选完成之后将料箱输送回立体仓库继续存储[1]。将跨层穿梭车双提升机系统应用到电商环境下的仓储作业中，以自动化智能设备代替人工作业，实现智能、高效、可靠拣选，对实现海量订单的快速、准确拣选具有重要意义。

跨层穿梭车双提升机系统是一种新型的自动化仓储设备，目前国内外学者对于不同形式的穿梭车系统任务调度问题进行了研究。Zou等[2]通过分析多层穿梭车系统建立了Fork-join 排队网络模型，并通过最大熵法（Maximum Entropy Method，MEM）求解，分析对比了穿梭车和提升机在并行作业命令和顺序作业命令两种策略下系统的性能；Ekren 等[3]和 Tappia 等[4]考虑穿梭车和提升机之间的制约关系，建立了半开环排队网络模型来求得系统的主要性能指标；牟善栋[5]研究了多层穿梭车仓储系统（Multi-tier Shuttle Warehousing System），并指出作业效率的影响因素，建立了货位分配和任务调度优化模型，通过蚁群算法和非支配遗传算法分别对两个模型进行求解；吴颖颖等[6]使用耦合因子描述订单之间的相互关系，对“货到人”系统中每个拣选台的拣选任务进行分配和排序，使用改进的K-Means聚类算法对问题进行求解；邹霞等[7]通过分析设备运动轨迹、设备运动时间模型、作业时间构成及多作业间的时序关系，建立多层穿梭车系统作业时间模型，研究货架结构和订单密度对系统效率的影响；张娜[8]使用半开环排队网络对跨层穿梭车系统进行建模，对其最优设备配置及出库任务调度进行研究；杨玮等[9]对双载式多层穿梭车系统复合作业路径优化问题进行了研究，使用混合植物遗传算法实现调度优化模型的求解。

目前，对于穿梭车系统任务调度和订单排序的研究都以一批订单出库时间最短为优化目标，缺乏对于订单交货时间限制的研究。柳赛男[10]在自动导引车系统的调度方法中加入优先级策略，采用云模型对调度任务进行优先级评价，并设计了基于文化算法的优化算法对问题进行了求解；胡建伟[11]分析环形穿梭车系统运行原理和仓库任务调度原则，对调度管理系统进行开发，并在调度过程中对任务优先级的评估体系和评价方法进行了研究。

基于以上研究，在跨层穿梭车双提升机系统的调度策略中引入交货时间限制，以穿梭车为服务节点建立了出库调度时间模型。针对穿梭车系统出库任务作业方式，提出使用蚁群-粒子群双层智能算法将任务调度问题分两步进行求解，并使用随机变异改进粒子群算法，提高了算法的求解性能。最后，通过对比实验，证明了模型和算法的有效性。

2 问题描述与分析

2.1 跨层穿梭车双提升机系统模型

跨层穿梭车双提升机系统采用料箱为存储和拣选单元，系统构成如图1所示，由穿梭车换层提升机、货物提升机、巷道穿梭车、高层货架、料箱输送线以及拣选台组成[12]，实现库存料箱存储和拣选出库作业。

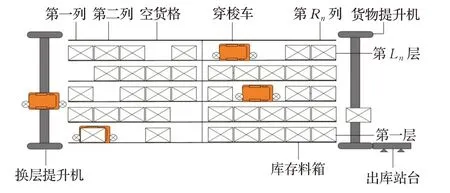
图1 跨层穿梭车双提升机系统侧面图

该系统采用穿梭车并行作业，货物提升机串行作业出库的协作方式，首先由穿梭车从指定货位拿取料箱，送到巷道首端，然后由货物提升机将料箱送到一层Input/Output 站台（I/O 口），完成一次料箱拣选出库任务。系统出库作业流程如图2所示。

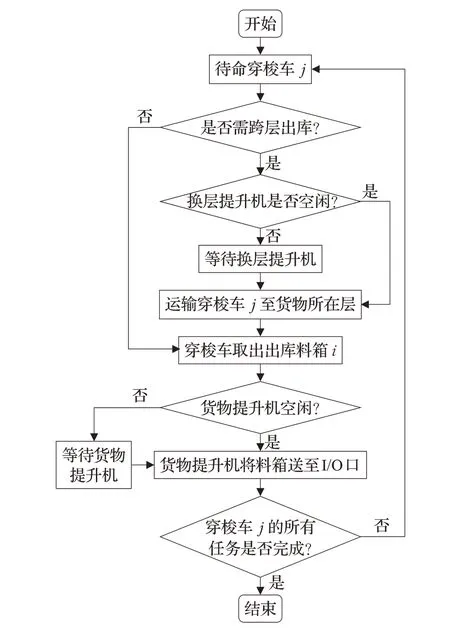
图2 跨层穿梭车双提升机系统订单出库流程

定义1O={(1,l1),(2,l2),…,(i,li),…,(Q,lQ)}表示出库任务集合，其中，i表示任务序号，li表示待出库任务料箱货位信息。

定义 2S={(1,q1),(2,q2),…,(j,qj),…,(m,qm)} 表示巷道穿梭车集合，其中，j表示穿梭车序号，qj表示该穿梭车的任务量。

本文所要求解的任务调度问题可以描述为一种分配方案问题A={o→s}，其中o∈O,s∈S，所得到的分配方案即为所求最优任务调度方案。

穿梭车系统在执行出库任务时，应满足以下条件：

（1）每个出库任务对应的料箱货位信息和穿梭车编号唯一。

（2）穿梭车执行出库任务时每次只能拿取一个料箱，送至巷道首端后申请货物提升机调度，将料箱交接给货物提升机之后才可离开，继续执行下一任务。

（3）跨层提升机、货物提升机的调度遵循先到先服务的原则（First-Come，First-Served，FCFS），若有多于一辆穿梭车同时提出调度申请，则提升机优先响应编号较小的穿梭车申请。

（4）系统初始时间记为0，跨层提升机和货物提升机都在第一层，穿梭车位置随机初始化。

（5）为防止碰撞和死锁现象，每层只允许一辆穿梭车进入，该层锁定，穿梭车离开后解锁，允许其他穿梭车进入。

2.2 订单拣选出库作业流程分析

2.2.1 穿梭车执行出库作业时间建模

跨层穿梭车双提升机系统由仓库管理系统（Warehouse Management System，WMS）将一个时间窗内的出库任务进行汇总，仓库控制系统（Warehouse Control System，WCS）将这些出库任务进行排序优化，最终下发给硬件设备完成出库任务。通过对穿梭车和跨层提升机、货物提升机的配合作业流程进行分析和优化，提高系统的作业效率，减小时间窗内订单出库总时间，同时降低拣选任务出库超时率。三者之间的配合作业如图3所示。

图3 穿梭车与提升机配合作业流程

穿梭车接到料箱出库任务后，由待命状态进入接受任务状态，此时穿梭车需判断是否需进行跨层作业。如果穿梭车与出库料箱不在同一层，穿梭车首先水平运动至巷道尾端，申请跨层提升机调度服务并等待提升机响应，若此时跨层提升机空闲，会立即响应穿梭车申请并前往该层完成穿梭车交接，将穿梭车垂直运输到出库料箱所在层，提升机进入待命状态；如果穿梭车与出库料箱在同一层，穿梭车水平运动至出库料箱所在货位，利用自身货叉完成取料箱动作。

载有出库料箱的穿梭车水平运动至巷道首端，申请货物提升机调度，提升机按照FCFS 原则响应穿梭车申请，前往至穿梭车所在层完成货物交接，此时穿梭车进入待命状态。货物提升机将料箱送至出库站台，完成I/O 交接，料箱出库任务完成。此时货物提升机进入待命状态，直到响应下一辆穿梭车调度服务申请。

将穿梭车看作服务节点，则固定时间窗内的任务出库总时间可定义为最大穿梭车工作时间与货物提升机最后一个任务执行时间之和。根据任务执行过程建立穿梭车j完成所分配的qj个出库任务所需时间数学模型Tj：

其中：

式中，Xij和δij为指示决策变量，当指定穿梭车j执行任务i的出库任务时，Xij为1，否则为0；当穿梭车需要执行跨层取货任务时，δij为1，否则为0。为穿梭车j执行任务i出库时换层所用的时间；为穿梭车j执行任务i出库时在取货层水平运动所用的时间；为穿梭车j执行任务i出库时等待货物提升机响应的时间；tsp为穿梭车取料箱或者放料箱的时间；tH为穿梭车从巷道首端运动到巷道尾端所用的时间，为固定常数；为穿梭车j执行任务i出库时等待换层提升机响应的时间；为穿梭车j执行任务i出库时，载有穿梭车的提升机垂直运动到出库订单所在层所用的时间；tcp为换层提升机装载或者卸载穿梭车的时间。

2.2.2 动力学分析

设穿梭车系统货架层高为rh，货架列宽为rw，货架层数为Ln，货架列数为Rn，出库任务i的货位坐标为(mi,ni)，mi=1,2,…,Ln，ni=1,2,…,Rn，mi表示货架层数编号，ni为货架列数编号。穿梭车水平运行最大速度vh，提升机垂直运行最大速度vv，穿梭车水平运行加速度ah，提升机垂直运行加速度av。通过运动特性对设备运行时间进行具体分析。

（1）穿梭车在执行跨层出库任务时，首先要从巷道首端运动到巷道尾端，其运动时间为一固定值tH：

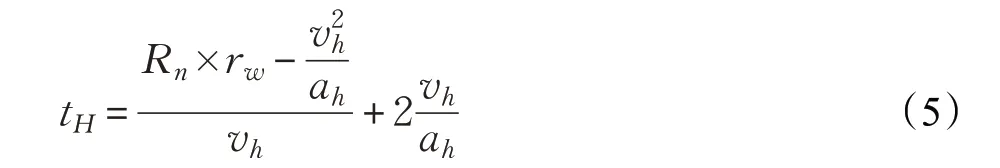
（2）假设出库货物距离巷道口的距离为S1(S1=mi×rw)，根据动力学运动公式，穿梭车执行同层取货任务时，穿梭车在取货层水平运动所用的时间th：

同理，可以得到穿梭车执行跨层取货任务时在取货层水平运动所用的时间。

（3）假设出库货物距离第一层的距离为S2(S2=(ni-1)×rh)，则货物提升机执行一个出库任务垂直运动的时间tv：

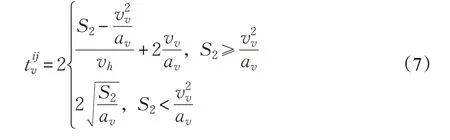
（4）穿梭车执行跨层出库任务时，假设穿梭车与空载换层提升机之间的距离为S3(S3=|nj-nc|×rh)，则空载换层提升机垂直运动到穿梭车所在层的时间：

其中，nj表示穿梭车所在层编号，nc表示换层提升机所在层编号。

（5）假设穿梭车与待出库货物之间的垂直距离为S4(S4=|ni-nj|×rh)，则载有穿梭车的换层提升机垂直运动到货物所在层所用时间：

2.2.3 穿梭车等待时间

按照FCFS原则，当穿梭车申请提升机进行服务时，如果提升机的上一个任务未完成，则穿梭车需等待提升机响应。根据申请服务类型的不同，可以将穿梭车等待时间分为等待换层提升机服务响应时间和等待货物提升机服务响应时间。

（1）等待换层提升机服务响应时间

假设当前穿梭车服务申请为换层提升机的第h个任务，则等待时间：

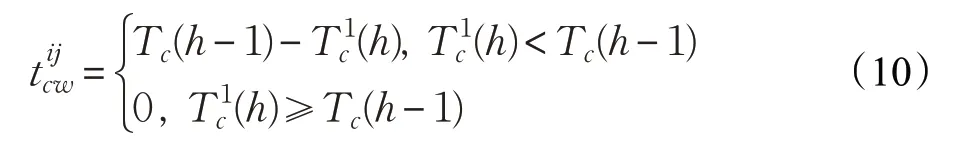
其中，表示穿梭车提出申请换层提升机服务的时间，Tc表示换层提升机完成任务的时间。

（2）等待货物提升机服务响应时间

假设当前穿梭车服务申请为货物提升机的第l个任务，则等待时间：

其中，表示穿梭车提出申请货物提升机服务的时间，Ts表示货物提升机完成出库任务的时间。

2.3 料箱拣选出库任务调度优化模型

2.3.1 固定时间窗内料箱拣选出库总时间

在跨层穿梭车双提升机系统的运行环境中，所有的穿梭车都是以并行模式运行，分配到同一穿梭车的出库订单将在等待队列中顺序执行，因此，在整个任务调度的过程中，建立出库总时间模型：

约束条件为：

公式（13）表示完成订单出库任务的总时间不得小于第一个订单水平作业时间与所有订单的货物提升机连续作业时间之和，即货物提升机等待时间为零时，完成订单出库任务所用总时间；公式（14）表示穿梭车执行跨层出库任务时，必须先申请换层提升机服务再申请货物提升机服务，且两次申请调度的时间差不得小于穿梭车到目标层取料箱所用时间；公式（15）表示穿梭车完成出库任务i的时间不得早于货物提升机响应该出库任务的时间加上货物提升机到达出库货物所在层所用时间以及与货物交接所需时间；公式（16）表示每个出库订单任务对应的穿梭车编号唯一。

2.3.2 料箱拣选任务超时时间

已知出库任务集合O和调度方案A，经出库过程仿真后得到该调度方案各拣选任务的出库完成时间集合，任务出库时限集合。

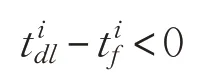
此时，则称任务i出库超时。其中，表示出库任务i实际完成时间，表示出库任务i的出库时限。

将任务出库的超时率Rtimeout和平均超时时间Ttimeout引入到任务调度模型中，给出计算公式：

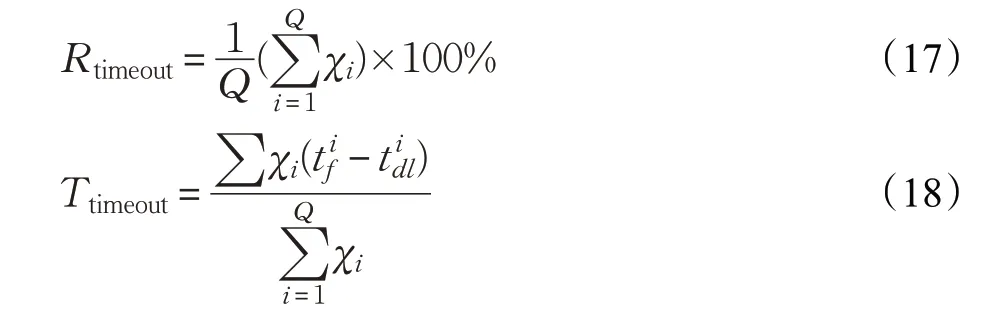
χi表示决策变量，χi={0,1},i=1,2,…,Q，任务i超时出库时记为1，否则记为0。

结合公式（12），将出库任务调度数学模型转换为如下形式：

其中，θ1、θ2为权重系数，θ1+θ2=1。基于式（19）的任务调度模型充分考虑了出库任务完成总时间和出库任务时限的要求，符合穿梭车系统的任务调度特点及要求。

3 蚁群-粒子群双层智能优化算法设计

跨层穿梭车系统的任务调度问题，可以分解为两部分进行求解：一是对穿梭车指派出库任务；二是对特定穿梭车进行出库任务排序。针对这一特点，使用蚁群-粒子群双层智能优化算法，首先利用蚁群算法将出库任务分配给各穿梭车，再将分配结果输入粒子群算法，对每辆穿梭车的出库任务进行排序，结合系统过程仿真寻找最优调度方案。

3.1 针对跨层穿梭车双提升机系统的算法编码

解决跨层穿梭车双提升机系统的任务调度问题，根据2.1 节中对调度方案的定义，构造了基于订单的编码方式，编码长度为，其粒子构成为(p1,p2,…,pn-1,pn)，其中pi表示一个出库任务编号。以9个订单，3辆可调度穿梭车为例，编码C=(3,4,6,2,5,8,1,7,9)即为一种可行编码，C(1)=3 表示订单3是穿梭车1的第一个出库任务，C(6)=8 表示订单8是穿梭车2的第三个出库任务，以此类推。解码时将各穿梭车对应的所有出库任务分解出来，例如，穿梭车1 对应的订单序列为{3，4，6}。以矩阵形式表示调度方案，通过跨层穿梭车双提升机系统过程仿真计算该出库方案的出库总时间。具体描述如下：

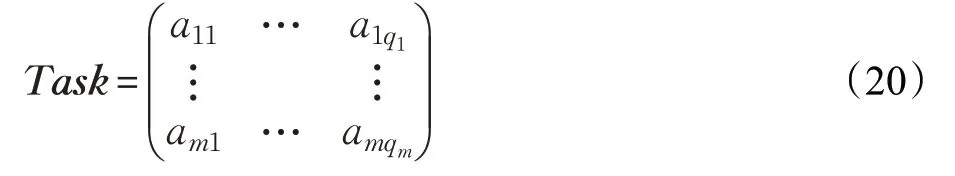
其中，Task代表一个任务调度方案，ajs表示订单编号ajs的订单为穿梭车j出库顺序中第s个出库任务。根据编码规则及调度原则，上述矩阵应有这样的性质：

（1）由于穿梭车的任务量不确定，矩阵的列数n=max{1,2,…,qm}。

（2）矩阵列数n=max(qj),j=1,2,…,m。当qj ＜n时，ajqj之后的元素记为0。

对于解码过程中产生的非可行解，采用罚函数的方法减小其适应度值，逐渐淘汰产生的非可行解。

3.2 蚁群算法设计

算法第一层将出库任务分配给不同的穿梭车，即确定穿梭车j的任务量qj以及相应的出库任务编号i。使用最大最小蚁群算法（Max-Min Ant System，MMAS）[14]，对每条路径信息素浓度设置最大最小值，每次循环中只对最优蚂蚁所走路线进行信息素增强。

MMAS 算法的目标是使各穿梭车的换层距离最短，即按照算法得出的分配方案穿梭车换层次数最少，从而减小订单出库任务总时间。在算法中，把出库任务看作蚂蚁要游历的结点，按照转移概率为每辆穿梭车选择出库任务，当所有出库任务所需穿梭车选择完毕，将分配结果作为输入值，形成粒子群算法的初始粒子。

穿梭车的总换层距离采用公式（21）进行计算：

其中，Ls表示穿梭车j的第s个出库任务所在层。

3.2.1 状态转移概率

蚂蚁在转移过程中，从任务i1移动到任务i2的转移概率[14]为：

公式（21）表示穿梭车j的出库任务中订单i2与订单i1的垂直距离越短，即穿梭车的换层时间越短，则选择订单i2作为订单i1之后出库任务的概率越大。

3.2.2 信息素更新

初始信息素浓度τi1,i2(0)=τmax，蚂蚁完成一次订单遍历后对最佳路径上的信息素浓度进行增强[15]，更新公式为：

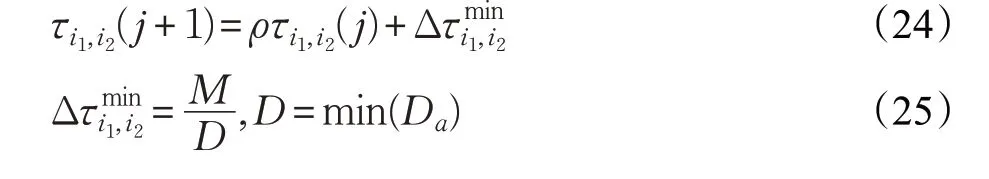
其中，ρ为信息素挥发系数，ρ∈(0,1)，M为信息素浓度系数，D为最优分配方案的穿梭车跨层总距离。τi1,i2(j)∈[τmin,τmax]，当τi1,i2(j)＞ τmax，取τi1,i2(j)=τmax；当τi1,i2(j)＜τmin，取τi1,i2(j)=τmin。

3.3 粒子群算法设计

离散粒子群算法（Discrete Particle Swarm Optimization，DPSO）作为算法第二层对穿梭车的订单任务进行排序，以出库总时间最短为优化目标，借鉴遗传算法中的交叉变异原理，使用置换序列对粒子进行更新，对调度问题进行优化求解。在调度求解的过程中，对基本DPSO算法进行以下改进：（1）在初始解产生方面，采用蚁群算法分配结果作为初始解，而不是采用随机产生初始解的方式；（2）在粒子更新过程中加入随机置换，增加粒子的种群多样性，避免算法早熟收敛于局部最优；（3）提出置换复杂度的概念，通过设置不同的置换复杂度，合理控制算法的全局搜索能力和局部搜索能力。

3.3.1 适应度函数

结合公式（19），给出DPSO 算法的适应度函数的形式：

3.3.2 粒子的速度和位置更新方法

穿梭车任务排序问题属于整数组合优化问题，DPSO算法重新定义更新公式对粒子进行更新[16]。

（1）置换因子：粒子的位置记为X，置换因子ch(p1,p2)表示交换粒子中p1和p2的位置，由一个或者多个置换因子组成的序列构成置换序列，记为CH=(ch1,ch2,ch3,…,chn)。称置换因子的数量为置换序列的复杂度。

（2）加法算子⊕：矩阵与置换序列进行相加表示粒子按照置换序列进行变换。

（3）减法算子：矩阵运算A-B=CH表示粒子A可以通过置换序列CH变换为粒子B，由于粒子A变换到粒子B可以由多个不同的置换序列完成，因此将含有置换因子最少的置换序列作为最简置换序列CHsim。

（4）乘法算子⊗：数字与粒子相乘表示该粒子的每一个元素都乘数字。

给出粒子的速度和位置更新公式[17]：

其中，ω为惯性权重，c1为自我学习因子，c2为群体学习因子，r1、r2为（0，1）之间的随机数，为局部最优解，为全局最优解。

已知局部最优粒子Pid=(p1d,p2d,…,p(n-1)d,pnd) ，随机生成复杂度为N的置换序列，对该粒子进行置换变异。其中置换因子ch(px,py)，px,py∉P*。

置换复杂度能够很大程度上影响种群的多样性，较大的置换复杂度能够对粒子产生很大的扰动，从而增加种群的多样性，算法能够在全局范围内寻优，避免早熟收敛；随着置换复杂度的减小，种群多样性趋于稳定，算法收敛速度加快，局部搜索能力增强，粒子逐步向最优解靠近。因此，提出使用自适应技术控制置换复杂度，对粒子进行随机置换。其计算公式如下：

其中，fmin为所有粒子的最小适应度值，favg为所有粒子的平均适应度值。

3.3.4 惯性权重的调整

采用惯性权重随迭代次数减小的策略，使算法获得较快的收敛速度和良好的搜索性能。

其中，ωmax为初始权重值，ωmin为最终权重值，itermax为最大迭代次数，iter为当前迭代次数。

3.4 蚁群-粒子群双层智能优化算法流程

使用蚁群-粒子群双层智能优化算法求解出库任务调度问题的步骤如下：

步骤1初始化蚁群、粒子群算法各参数，iter=0，将生成的蚂蚁随机放入待出库任务节点。

步骤2对蚂蚁计算状态转移概率，选择下一个出库任务，并将放入已游历任务列表中。

步骤3蚂蚁游历完所有待出库任务节点，更新信息素；否则返回步骤2。

步骤4蚁群算法达到终止条件，输出最佳路径，并将结果输入粒子群算法，作为初始解；否则返回步骤2。

步骤5在初始解的范围内，随机生成初始粒子，并计算各粒子适应度值f 。

步骤6比较各粒子的适应度值，更新各粒子局部最优值和全局粒子最优值。

步骤7更新粒子位置和速度，并根据3.3.3 小节中方法对局部最优粒子进行随机变异。

步骤8若达到算法终止条件，输出任务调度最优解；否则返回步骤5。

算法流程图如图4所示。

3.3.3 基于置换复杂度的粒子随机变异

图4 蚁群-粒子群双层智能优化算法流程图

4 算例分析

为了验证本文提出的模型和算法的有效性，基于某电子商务企业的真实订单数据，使用MATLAB 软件进行仿真测试，求解其最优的出库任务调度方案。

该电商企业的穿梭车储分一体系统共有24 个巷道，每个巷道2 400个货位，其设备运行参数如表1所示。

表1 设备运行参数

为验证本文所提出模型的有效性，选取该系统中10 组出库任务进行仿真实验，每组实验包含50 个出库任务，部分出库任务信息在表2 中列出。将仿真结果与本文提出的模型计算结果进行比较，实验对比如表3所示。

表2 出库任务信息

表3 仿真实验与模型计算结果对比

由表中实验数据可知，对50 个出库任务进行出库仿真实验的平均出库时间为666.44 s，本文所提出模型的计算结果657.75 s，平均误差为6.84%，可以认为本文所提出的数学模型能够较为准确地对穿梭车系统的出库过程进行描述。

为验证本文提出的任务调度优化算法的有效性，随机选取该电商企业某一时间窗内6 组料箱拣选出库任务数据，对出库任务进行调度分配，搜索最优的出库任务调度方案。

在使用蚁群-粒子群双层智能优化算法寻找出库任务调度的最优出库方案时，算法参数采用“三步法”[18]方式进行配置：首先确定算法的种群规模，即蚁群算法的蚂蚁数和粒子群算法的粒子数num；粗调参数，即对取值范围较大的信息素权重系数α、启发式信息权重系数β、学习因子c1和c2参数等进行调整；微调参数，即对取值范围较小的信息素挥发系数ρ、惯性权重ω等参数进行调整。

分别以出库任务数量50、100、150进行算法参数调整测试，最终参数取值为：MMAS算法蚂蚁个数Ma/Q=2/3，τmax=1，τmin=0.1，α=1，β=5，ρ=0.9，M=10；DPSO 算法种群规模num/Q=0.2，ωmax=0.96，ωmin=0.26，c1=0.5，c2=0.7。两层算法均迭代200次，在CPU为1.80 GHz，运行内存8 GB的计算机上进行100次出库仿真实验，将实验结果与标准ACO、DPSO 算法进行比较，三种算法订单超时率Rovertime、平均超时时间Tovertime以及订单出库总时间F(X)的比较结果如表4所示。

表4 仿真实验结果对比

图5 为三种算法不同订单数量下跨层穿梭车系统料箱拣选出库作业任务超时率趋势图，包括ACO算法、DPSO算法、MMAS-DPSO算法实验结果。

图6 对三种算法在求解穿梭车系统任务调度方案时的出库作业总时间进行了分析，其中对比1 表示MMAS-DPSO 算法对比ACO 算法的出库效率提升率，对比2 表示MMAS-DPSO 算法相对于DPSO 算法的出库效率提升率。

对比实验结果，可以得出以下结论：

图5 不同订单数量下料箱出库任务超时率

图6 不同订单数量下出库效率提升对比图

在加入出库时限优化条件之后，三种算法出库任务超时率均优于未考虑出库时限时的实验结果，且MMAS-DPSO的优化效果最为明显。

在求解小规模订单任务调度方案(Q=50)时，三种算法优化性能相差较小，任务出库超时率均在5%左右，MMAS-DPSO算法求解调度方案任务超时率最低，仅为4%；当订单规模持续增大，ACO算法和DPSO算法所得出的调度方案订单超时率急剧增大，Q=300 时，PSO算法超时率增长至20%以上，而MMAS-DPSO算法在求解过程中具有良好的稳定性，订单超时率增幅较小，在Q＜250 时，任务超时率均小于5%。

随着订单规模持续增大，ACO算法和DPSO算法与MMAS-DPSO 算法求解调度方案的出库总时间差值逐渐增大，这是因为ACO 和DPSO 算法均使用订单随机平均分配给穿梭车的调度策略，未对穿梭车跨层距离进行优化，穿梭车换层次数多，从而增加了出库作业总时间，其中ACO 算法增幅最大，当Q=200 时，与MMASDPSO算法的出库时间差值已超过500 s。

MMAS-DPSO 算法在求解跨层穿梭车系统任务调度的过程中，通过蚁群、粒子群两层算法对调度方案进行分步求解，比单一的ACO、DPSO 算法求解所得结果具有更短的出库时间和更低的订单超时率，尤其在求解大规模出库任务调度中具有良好的优化性能，出库效率提升10%以上；在粒子群算法中引入出库任务时限作为寻优条件，将订单之间的相互关系作为优化的性能之一，使粒子在更新过程中向着订单出库超时最短的调度方案演变，在Q＜300 时，订单平均超时率为8.4%，比不考虑任务优先级的情况下使用MMAS-DPSO 算法实验值降低15%以上，调度方案的合理性更优。

5 结束语

本文对跨层穿梭车双提升机系统进行了建模与优化，建立了出库任务调度数学模型，并将出库任务期限引入任务调度策略；提出使用改进的蚁群-粒子群双层智能优化算法对任务调度问题进行求解，通过仿真实验证明了模型和算法的有效性。最后，将MMAS-DPSO算法与标准ACO 算法、DPSO 算法进行实验比较，结果表明本文所用算法在求解大规模出库任务调度的问题中具有明显的优势，得到更为高效的调度方案，更能适应电商环境下海量订单拣选出库要求，为跨层穿梭车系统的研究和应用提供了借鉴意义。

穿梭车系统在运行过程中，穿梭车同时接收订单入库和出库任务，而本文给出的调度策略只考虑了出库任务对穿梭车系统进行单一指令调度优化，进一步的研究可以同时考虑入库和出库任务对系统进行双指令调度优化。