引入动态调节学习率的SAE轴承故障诊断研究

唐 魏，郑 源，潘 虹，徐晶珺

1.河海大学 水利水电学院，南京 210098

2.河海大学 创新研究院，南京 210098

3.河海大学 能源与电气学院，南京 211100

1 引言

随着互联网、物联网的快速发展，当前社会数据的增长十分迅速，在轴承故障诊断领域更是如此[1]，形成海量的各种设备来源、各种形式的故障和正常数据，这导致属于浅层学习的传统轴承故障诊断方法具有无法充分挖掘数据深层特征的局限性[2]。深度学习作为大数据时代的产物，由于其具有多个隐含层，能够实现复杂非线性函数的表示，在特征自动提取上具有很多其他算法不可比拟的优势[3]。

深度学习目前较为成熟的算法有4 种[4]：深度置信网络（Deep Belief Network，DBN），卷积神经网络（Convolutional Neural Network，CNN），循环神经网络（Recurrent Neural Network，RNN），堆叠自编码网络（Stacked Auto-Encoder，SAE）。深度学习在轴承故障诊断领域也已经进行了大量的应用[5-9]，其中SAE网络的应用研究方面，Sun等[10]利用SAE实现轴承故障诊断，并分析了Dropout 对于故障识别率的影响；张西宁等[11]运用带标准化的堆叠自编码网络进行滚动轴承故障诊断研究；杜灿谊等[12]运用萤火虫算法优化SAE网络参数；侯文擎等[13]利用粒子群算法优化SAE 网络超参数；郑近德等[14]结合多尺度熵和自编码器进行滚动轴承故障诊断。

可以看出目前SAE 在轴承故障诊断领域的应用研究主要集中在超参数的优化、输入数据形式、不同样本数据长度和网络结构对准确率的影响的研究上，关于SAE网络反向微调的有标签数据量，文献[10-14]中多表示为少量有标签数据，很少有人进行量化研究和探究减少有标签数据的措施，如果能减少所需要的有标签数据量，则能大量减少人工标签的时间，节约人力成本。普通的深度学习网络采用一个固定的学习率，这样对学习率的设置需要大量经验，设置过大会导致难以收敛或跳过最优值，设置过小会导致收敛速度过慢，文献[15-23]研究了动态学习率解决这个问题，但其研究主要集中在CNN 和DBN 上，利用动态调节学习率加快收敛速度和收敛精度。

本文基于堆叠自编码网络进行轴承故障诊断研究，提出动态调节学习率取代原始的固定学习率进行预训练，通过不同有标签数据量反向微调，研究不同学习率和有标签数据量对于轴承故障分类识别的影响。

2 堆叠自编码深度神经网络

2.1 自编码器

自编码器（auto-encoder）是 Rumelhart 在 1986 年提出的一种单隐藏层神经网络[24]，其结构如图1所示，这种网络是在无监督学习的方式下，使得输入和输出尽可能保持一致。假设输入为n维的数据X，输出为n维的数据Y，输入数据通过全连接的方式加权求和，加上偏置之后在激活函数的作用下，得到隐藏层H，数据维度为k维，隐藏层再通过同种方式得到输出层，然后利用反向传播算法，以缩小输入、输出的差异为目标，对权值和偏置进行迭代更新，直到满足误差的要求或是迭代步数的要求。自编码器数学表达如下：

式中，Wa∈ Rn×k、Ws∈ Rk×n、ba∈ Rk、bs∈ Rk为需要优化求解的权值和偏置，σa(⋅)、σs(⋅)为激活函数。

图1 自编码器结构示意图

2.2 堆叠自编码网络

堆叠自编码网络（SAE）由 Hinton 于 2006 年对Rumelhart 提出的自编码器进行改进而来[25]，其结构图如图2所示。将自编码器的编码部分进行堆叠，即第一层自编码器的输入为原始数据，自此下一层自编码器的输入为上一层自编码器的隐藏层数据，最后给网络加上分类器，就构成了SAE。堆叠自编码网络采用的是预训练和反向微调相结合的训练方式，即先用大量的无标签数据进行无监督学习，自主提取特征，然后利用有标签数据对网络反向微调。预训练和反向微调过程采用的均是梯度下降算法。

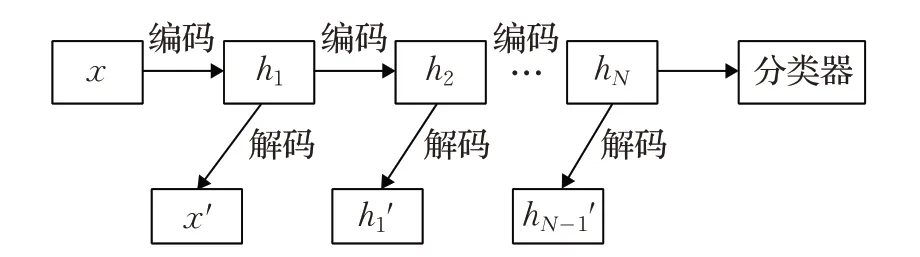
图2 SAE结构示意图

3 数据来源和数据处理

3.1 数据来源

实验数据源于美国西储大学（CWRU）轴承数据中心[26]，CWRU数据集是世界公认的轴承故障诊断标准数据集。所使用的轴承故障位置为外圈滚道、内圈滚道、滚动体，故障的程度为3 类，分别为0.18 mm、0.36 mm、0.54 mm，9 种故障数据加上正常的数据就得到了10 种状态的轴承数据，数据集为用加速度传感器采集的电机壳体的驱动端的振动，频率为12 kHz。每种状态使用中间位置的120 990 个节点的数据，取前50 990 个节点为训练数据，其余为测试数据。

3.2 数据处理

3.2.1 归一化

实验使用原始的轴承数据，只对振动数据进行归一化，归一化公式如下[8]：

3.2.2 数据集增强

设置每个样本的数据长度为1 000，为了得到更多的训练样本，采用滑动窗口重叠采样数据增强技术[27]，原理如图3 所示，偏移量设置为10，得到每种状态的训练数据的样本量为5 000，测试数据不进行重叠，得到每种状态的测试数据样本量为70，这样训练数据样本总和为50 000，测试数据样本总和为700。

图3 数据增强原理图

4 实验过程及结果

实验在MATLAB2014b 平台上进行，激活函数为sigmoid，输出分类器为softmax，使用GPU进行加速运算。

4.1 网络结构确定

设置恒定的预训练学习率为0.1，预训练迭代次数为700步，反向微调学习率为0.01，反向微调有标签样本占比为10%，迭代次数为1 000步，batchsize设置为100。根据文献[22]BP 神经网络关于隐含层节点数的经验公式：

其中，m为输入数据节点长度，n为输出数据节点长度，k为[0，10]以内的常数。结合实例，确定隐含层节点数为105。

为研究不同隐含层层数对于轴承故障分类识别的影响，设置隐含层层数分别为1、2、3、4、5、6层的对比实验，取十次结果的平均值作为最终结果，得到的准确率如表1。

表1 不同隐含层层数的结果对比

从表1可以看出，隐含层层数为3时准确率最高，当隐含层层数为6时，准确率随着层数的增加下降速度变快。以上结果说明，网络结构太浅不利于数据特征的表达，太深则会导致网络特征的丢失。

采用下一层隐含层节点数为当前层节点数的一半的策略对网络结构进行优化[28]，确定网络结构为[1 000-500-250-125-10]，并与其他网络结构进行对比分析，所有结果均为实验十次取平均值。

从表2 可以看出，采用[1 000-500-250-125-10]网络结构的准确率最高，在后续的研究中选取该网络结构。

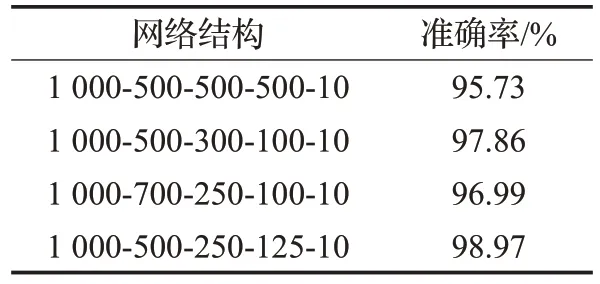
表2 不同网络结构准确率对比

4.2 动态学习率

梯度下降法训练SAE 网络实质就是利用损失函数对权重的偏导数迭代调整网络的权重，其中权值的更新计算公式如下：

式中，Wi和Wi+1是计算过程中第i次迭代和第i+1 次迭代过程中的权值，η为学习率，Li为损失函数。

学习率是训练过程中一个非常重要的参数[18]。过大的学习率会导致收敛困难或跳过最优解，而过小的学习率则会导致收敛速度过慢，增加计算时间，不利于效率的提高，为了解决这一问题，需要采用非恒定的学习率。

由于损失函数对权重的偏导数较为复杂，选取预训练中输入数据的重构误差作为学习率调整的依据，参考文献[16]，确定如下的学习率调整策略：

其中，h(i)为迭代次数为i时的学习率，h(i+1)为迭代次数为i+1 时的学习率，ΔLi为迭代次数为i(i ＞2)次时重构误差的梯度，采用向前差商法计算重构误差的梯度，求解方法如式（9）所示：

通过式（9）的计算，当重构误差波动下降时，得到的重构梯度为负，这样学习率便以较慢的方式减小，避免学习率减小过快。为了避免学习率过低导致梯度消失的问题，将学习率的范围限制在0.01～5范围内。动态调节学习率的预训练流程如图4所示。

分别设置固定学习率为0.01、0.1、0.2、0.3与该动态调节的学习率进行对比实验，动态调节的学习率初始值设置为0.2，其他网络超参数保持一致，得到的重构误差曲线如图5所示。

从图5 可以看出，学习率为0.2、0.1、0.01 和动态调节时，重构误差整体都随着迭代次数的增加而减小，在学习率为0.3时，在迭代初期网络发散，最终会陷入局部最优解；网络700 次迭代结束时，0.01 学习率并未稳定（未收敛），重构误差具有明显的下降趋势，0.1、0.2和动态调节学习率曲线基本稳定（收敛），其中动态调节学习率曲线稳定值比其他三者都低，0.2 固定学习率的重构误差稳定值小于0.1固定学习率对应的值。从重构误差下降速度上来看，在最初阶段，动态调节学习率和0.2固定学习率的重构误差下降速度最快，在迭代进行到20步左右时，动态调节学习率的重构误差下降速度超过0.2固定学习率，整体上，动态调节学习率达到稳定所需要的迭代步数最少。表3 展示了各种学习率网络迭代过程耗时和收敛时的重构误差，从表中可以看出采用动态调节学习率的收敛时间相比于较优的固定学习率要减少17.70%，重构误差下降了22.92%。

图4 动态调节学习率的预训练流程图

图5 不同学习率下的重构误差

表3 不同学习率对应的结果对比

4.3 不同有标签样本量

有标签样本占比为10%时，通过SAE预训练和反向微调，达到了98.97%的正确率，为了探究有标签样本量对于SAE网络反向微调过程的影响，进一步设置了有标签样本量分别占总样本量1%、2%、3%、4%、5%、6%、7%、8%、9%九个不同组。为了保证有标签样本占比越大，包含的信息越多，有标签样本的增加规则如图6 所示，图中2%有标签样本由前面的1%有标签样本加上另外的1%有标签样本组成，3%有标签样本由前面的2%有标签样本加上另外的1%有标签样本组成，以此类推。

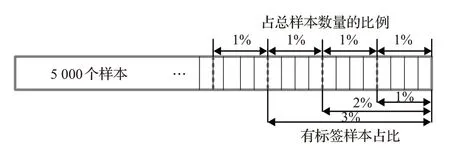
图6 有标签样本的增加规则

分别采用0.1固定学习率和动态调节学习率的预训练方式得到的权值和偏置进行有监督的反向微调，故障分类准确率结果为进行十次实验得到的平均值，实验结果如图7 和图8 所示，图8 为动态调节学习率的结果。由图7 可以看出，相比于固定学习率，动态调节学习率在相同的有标签样本量下得到的准确率更高，因此达到相同的准确率，动态调节学习所需的有标签样本量更少；准确率随着有标签样本量变化可以分成两段，第一段是在有标签样本量从10%减少到6%时，准确率随着有标签样本量的减少下降较慢，第二段是在有标签样本量小于6%时，识别率随着有标签样本量减少，下降速度比第一段快。从图8 可以看出，有标签样本量越多，达到90%准确率所需要的迭代步数越少，网络收敛所需要的迭代次数也减少，收敛也越来越容易，在综合考虑迭代次数和准确率，当有标签样本量占比为8%左右时，所得到的结果最优。

图7 两种学习率准确率变化图

图8 不同有标签样本量准确率随迭代步数变化图

从表4可以看出，该动态调节学习率的SAE模型在故障识别准确率上较以往研究中所使用的模型高。

表4 准确率结果对比

5 可视化

t 分布随机邻域嵌入算法（t-distributed Stochastic Neighbor Embedding，t-SNE），由Laurens van der Maaten和 Geoffrey Hinton 于 2008 年提出，t-SNE 算法在降维、聚类、可视化的应用上取得了良好的效果。利用t-SNE对10%、5%、1%有标签样本量的第三隐含层的数据进行可视化，结果如图9～图11所示。

图9 1%有标签样本可视化

图10 5%有标签样本可视化

从图9～11可以看出，图11的故障区分效果最好，每种故障类型都能区分，图10相对于图11，有少数故障类型未能区分，图9有较多的数据重叠。对比图9、图10以及图11，三者都实现了故障的聚类，只是缺少有标签样本对各种故障进行区分，导致故障识别准确率的下降。

图11 10%有标签样本可视化

6 结束语

本文从普通的SAE 模型出发，通过对比实验的方法，确定了最优网络结构，在此基础上，从学习率的角度改进了普通SAE模型，并使用不同数量的有标签样本进行网络的微调。通过以上研究得到如下结论：

（1）提出了一种动态调节学习率方法，改进了SAE网络。该方法在初始时刻给予一个较大的学习率，并在迭代过程中依据重构误差梯度的正负，确定不同学习率的减小策略，为SAE 网络动态更新一个较合适的学习率。实验表明，相比固定学习率的SAE网络，该动态调节学习率的SAE 网络预训练收敛时间减少17.70%，重构误差下降22.92%，相对于以往的普通模型，故障分类识别的准确率更高。

（2）对于SAE 网络，反向微调过程中轴承故障有标签样本量越多，故障分类的准确率越高，模型更快或更容易收敛，当有标签样本量占超过6%时，随着有标签样本量的减少，准确率降低幅度较小。

（3）相比于固定学习率方式，采用该动态调节学习率进行预训练得到的SAE网络权值和偏置，经过反向微调，在达到相同准确率下所需的有标签样本量更少。