往复压缩机气缸活塞应力和变形有限元分析
2020-10-19郭天星卢福志
肖 强,曾 妍,郭天星,卢福志
(1.中国石油集团济柴动力有限公司成都压缩机分公司,四川成都 610100;2.长城钻探工程有限公司苏里格气田分公司,辽宁盘锦 124010;3.加拿大中加压缩机撬及管道工程公司,卡尔加里加拿大)
1 引言
往复压缩机主要通过活塞在气缸中的往复运动来达到压缩气体的目的。活塞在气缸中运动时承受的载荷主要包括安装预紧力、热应力、气体压力及惯性力等载荷。气缸活塞在这些载荷作用会产生较大的应力及变形。另外,活塞设计时还要考虑到重量最小化以达到降低惯性力及提高机械效率等目的以及活塞运行时需要满足其与气缸之间的密封要求。因此,气缸活塞需要选择低密度、高强度的材料以及合理的结构设计来满足机组运行要求。
本文使用ANSYS有限元程序,分别对2种铝活塞结构的变形和应力进行了有限元分析计算。通过对比分析2种铝活塞结构,说明其结构优劣,以及优化和改进的方向,为固化活塞典型设计结构提供参考依据。
图1表示了改进前的传统铝活塞结构,该活塞结构采用6根连接螺栓将2个活塞半体连接在一起,活塞半体采用6根加强筋。图2则表示了改进后的铝活塞结构,该活塞结构采用过盈配合将2个活塞半体连接在一起,活塞半体采用8根加强筋。
2 改进前铝活塞有限元分析模型
图3和图4表示了改进前铝活塞结构的有限元分析模型。根据其结构特点和载荷特性,用ANSYS分析程序生成有限元模型。该有限元模型包括了活塞本体、活塞杆、六角螺母和连接螺栓等部件,由549804个三维固体Solid186(20节点立方体二次单元) 与Solid187(10节点四面体二次单元)。该有限元分析模型使用了几何非线性大变形理论,即被分析体刚度可随几何变形改变,以精确分析活塞变形与应力的关系。
考虑到活塞运动属性及与活塞杆的相对位置关系,将可法向变形的远端位移约束施加于活塞杆远端(十字头端),以尽可能降低边界效应对活塞体应力分析的影响。
分析载荷包括如下几个部分:
(1) 安装预紧力,按活塞安装螺栓预紧力矩100 Nm,活塞杆预紧力矩4500 Nm计算。
(2) 热应力,按安装温度20 ℃、气缸内部150 ℃计算。
(3) 气体压力,按机组运行工况中正、反向最大压差分别考虑。
(4) 惯性力,按活塞组件总质量219 kg,根据活塞运动方向施加相应加速度进行模拟。
本有限元分析包括多个有限元模型。每个有限元模型分析都求解活塞组件在安装螺栓及活塞杆预紧力、热应力、气体压力、和惯性力作用下的应力分布。
整个计算过程采用4个荷载步逐步加载完成。其中,第一个荷载步是施加安装螺栓及活塞杆预紧力;第二个荷载步是施加热温度载荷即热应力;第三个荷载步是施加活塞进、排气2个端面上的压力差;第四个载荷步是施加惯性力荷载。
在每个荷载步计算过程中,启动了大变形静力分析及自动时间步长选择。每个荷载步设置2个子步,至多25个子步。程序启用16个CPU迭代求解,求解方法由程序自动选择。

图1 改进前铝活塞结构三维模型

图2 改进后铝活塞结构三维模型

图3 改进前活塞整体结构有限元分析模型
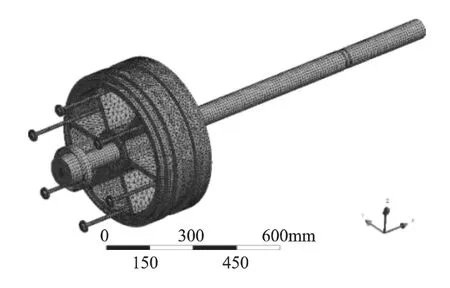
图4 改进前活塞半体与活塞杆结构有限元分析模型
3 改进前铝活塞有限元分析结果
图5显示了改进前活塞体在分析载荷(包括安装预紧力、热膨胀应力、正向气体压力和惯性力)作用下的变形分布计算结果。活塞体两端面间最大相对位移计算值为1.14 mm。图6显示了活塞体在该载荷作用下的VonMises应力分布计算结果。计算得到的最大VonMises应力为184.2 MPa,发生于活塞体与螺栓接触的局部端面。
图7显示了安装螺栓在该载荷作用下的VonMises应力集中,螺栓局部最大集中应力超出其材料屈服极限540 MPa。而且,随着载荷增加,螺栓屈服部位范围也进一步增加。图8显示了安装螺栓在该载荷作用下的变形。

图5 改进前活塞的变形分布

图6 改进前活塞的VonMises应力分布

图7 活塞安装螺栓的VonMises应力集中

图8 活塞安装螺栓的变形
4 改进后铝活塞结构有限元分析
图9和图10表示了改进后铝活塞结构的有限元分析模型。根据其结构特点和载荷特性,用ANSYS分析程序生成有限元模型。该有限元模型包括了活塞本体、活塞杆、盖侧墙板、锁紧螺母等部件,由424001个三维固体Solid186(20节点立方体二次单元) 与Solid187(10节点四面体二次单元)。该有限元模型同样使用了几何非线性大变形理论,即被分析体刚度可随几何变形改变,以精确分析活塞变形与应力的关系。

图9 改进后活塞整体结构有限元模型

图10 改进后活塞半体与活塞杆结构有限元模型
除没有安装螺栓外,改进后活塞有限元分析的边界条件、载荷以及求解步骤与改进前活塞有限元分析相同,此处不再重复。
5 改进后铝活塞结构有限元分析结果
图11显示了改进后活塞体在分析载荷(包括安装预紧力、热膨胀应力、正向气体压力和惯性力)作用下的变形分布计算结果。活塞体两端面间最大相对位移计算值为1.22 mm。图12显示了活塞体在分析载荷作用下的Von Mises应力分布计算结果。计算得到的最大Von Mises应力为145.4 MPa,发生于活塞体加强筋与中轴倒角处。
图13和图14显示,在活塞加强筋与中轴连接的倒角处有明显的局部应力集中。该局部应力集中产生的最大VonMises应力值为145.4 MPa,约为铝活塞材料抗拉强度的57%。
6 分析结果讨论
6.1 活塞本体设计的安全性准则及评估
改进前和改进后两种铝活塞本体结构均使用了ZL108脆性材料。按脆性材料失效判断准则,活塞本体设计必须确保其最大主应力(拉应力) 低于材料抗拉强度值,这样设计才是安全的。

图11 改进后活塞的变形分布

图12 改进后活塞的VonMises应力分布

图13 改进后活塞结构应力集中示意图(盖端)

图14 改进后活塞结构应力集中示意图(轴端)
传统设计过程中一般要求使用3~4的安全系数。这是因为要考虑到设计计算中一些难以计及的因素,如应力集中影响等。如使用有限元分析计算方法,在设计计算中已计入了传统安全系数要考虑的那些因素(如应力集中影响等),则不必再要求使用3~4的安全系数。可以使用材料的抗拉强度直接作为其一次许用应力。这与美国ASME BPV Section VIII Div 2标准中所要求的,在基于分析的设计中,计算的部件一次应力最大可达材料屈服(或抗拉) 强度的理念是一致的。
郁永章教授等所著的《容积式压缩机技术手册》 中,也提出了盘形与鼓形活塞端面的最大允许弯曲应力值和毂部最大允许剪切应力值,亦可作为活塞本体安全设计的参考。
前面所述2种铝活塞结构的有限元分析结果表明,计算得到的活塞本体上的最大主应力(拉应力)均低于活塞本体材料ZL108的抗拉强度255 MPa。参照本节活塞本体设计的安全性准则,可见2种铝活塞结构均满足压缩机安全使用要求。
6.2 2种铝活塞结构有限元分析结果比较
通过比较前述2种铝活塞结构的有限元分析结果,可以看到改进后活塞结构设计明显优于改进前活塞结构设计:
(1) 改进后活塞结构的最大VonMises应力比改进前活塞结构的最大应力值小很多。计算得到的改进前活塞结构最大VonMises应力值为184.2 MPa,而改进后活塞体结构的相应应力值则为145.4 MPa。
(2) 计算得到的改进前活塞结构安装螺栓名义应力为430 MPa,螺栓颈部最大局部VonMises应力已超过材料屈服极限,螺栓存在断裂危险。但改进后活塞结构设计无安装螺栓,没有该失效风险。
(3) 计算得到的改进前活塞体结构两端面间最大相对变形为1.14 mm,改进后活塞体结构两端面间最大相对变形为1.22 mm,两者相近。
7 进一步优化改进分析
进一步优化改进措施包括将改进后活塞结构的8根加强筋减少到6根加强筋。图15显示了进一步优化改进后的活塞结构几何模型。除加强筋数量减少外,其余部分结构、结构接触连接、承受载荷、分析方法等均与原改进后活塞时的情况相同。
图16显示了6根加强筋铝活塞体在分析载荷(包括活塞杆安装预紧力、热膨胀应力、正向气体压力和惯性力) 作用下的变形分布计算结果。活塞体两端面间最大相对位移计算值为1.20 mm。
图17显示了该活塞体在分析载荷作用下的VonMises应力分布计算结果。计算得到的最大Von-Mises应力为170.1 MPa,发生于活塞体加强筋与中轴倒角处。
图18和图19显示了加强筋与中轴连接倒角处有明显的局部应力集中。该局部应力集中产生的最大VonMises应力值为170.1 MPa,约为铝活塞材料抗拉强度的67%。
从上面有限元分析结果可知,将铝活塞结构的8根加强筋减少到6根加强筋后,活塞结构变形量的变化基本相同,其最大应力也在设计准则允许值范围内。但考虑到将铝活塞结构的8根加强筋减少到6根加强筋后,可相应简化生产过程和降低生产成本,设计时可采取此优化措施。

图15 6根加强筋的活塞结构几何模型

图16 6根加强筋铝活塞的变形分布
8 结论

图17 6根加强筋铝活塞的VonMises应力分布

图18 6根加强筋活塞应力集中示意图(盖端)

图19 6根加强筋活塞应力集中示意图(轴端)
本文采用ANSYS有限元程序,对2种铝活塞进行了应力和变形分析。分析结果表明,对同样的活塞材料和载荷,改进后铝活塞的最大应力比改进前的最大应力值小很多。同时,改进后铝活塞结构由于没有安装螺栓,从而避免了螺栓失效风险。因此,同样条件下改进后的活塞结构优于改进前。改进后的活塞结构还可通过减少加强筋的方法来作进一步优化。但改进后活塞结构依然存在应力集中的问题。虽然该应力集中并不影响活塞的安全运行,还是需要通过更深一步的分析和研究来优化结构从而消除或减少应力集中,提高活塞安全性及延长活塞寿命。
