基于可调品质因子小波和簇稀疏增强的磁异常信号特征提取研究
2020-10-19贺王鹏陈彬强张绍华
贺王鹏,胡 洁,陈彬强,张绍华,易 忠
(1. 西安电子科技大学 空间科学与技术学院,西安 710071; 2. 厦门大学 航空航天学院,厦门 361005;3. 北京卫星环境工程研究所,北京 100094)
0 引言
地球上的磁性物体存在固有磁场并能产生感生磁场,这些磁场与地磁场相互作用,会改变物体附近地磁场的分布情况,使得实际测量的地磁场强度和理论磁场强度有所差异,这种现象称为局部地磁异常现象。磁性运动目标产生的磁异常信号包含着很多重要信息,可反映目标的方位、距离、速度等[1]。对磁异常信号进行探测并反演,可追踪和定位目标[2]。然而,由于磁异常信号微弱,探测过程中信号又易受到强噪声背景的干扰,导致磁异常信号特征提取的难度极大。因此,如何从复杂的观测信号中有效地去除测量信号中的噪声,精确提取出隐藏在复杂噪声干扰中的有用特征信息,是磁异常信号探测的关键环节,对后续反演结果的准确性具有重要的意义。
信号处理与特征提取是模式识别等领域的基础和关键,在计算机视觉、语音分析等诸多方面得到了蓬勃发展。近年来,在工程中常见的傅里叶变换和小波变换等信号处理与特征提取方法,其基本思想都是对基函数进行分解以获得与特征波形相吻合的基函数,使提取的信号具有稀疏特性[3]。其中,基于小波的特征提取方法受到了国内外学者们的青睐[4]。2009年,小波分析领域著名学者Mallat从稀疏的视角阐述了小波在各个领域的应用。在理想的特征提取分析中,小波的品质因子应该和待分析信号的振荡特性具有最佳匹配。例如,具有相对低品质因子的小波适合处理分段光滑的信号,而具有较高品质因子的小波则适合分析振荡信号。然而,对于传统方法如离散小波变换,其品质因子固定且值较小,虽然能够实现分段光滑信号,如非振荡瞬态成分等的稀疏表示,但难以实现高振荡成分的稀疏表示[5]。
可调品质因子小波变换(tunable Q-factor wavelet transform, TQWT)[6]能避免传统离散小波变换的缺陷。TQWT可以灵活地设置小波基函数的品质因子,来调节小波滤波器的特性,使小波的振荡特性与待分析信号的振荡特性相吻合,进而增强信号表示的稀疏性。然而,对于具有簇特性的信号,小波基函数展开方法在最大化稀疏特征提取方面仍缺乏自适应性,难以最佳匹配稀疏的特点,从而影响特征提取的性能。针对此类信号的稀疏处理,需在小波分解降噪结果的基础之上采用簇稀疏技术进一步提高特征提取的效果。重叠簇收缩(overlapping group shrinkage, OGS)算法是一种新兴的、有效的针对具有簇特性信号的提取算法[7-8],能充分利用特征波形具有的簇稀疏结构来增强特征提取结果。
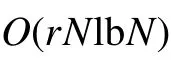
1 可调品质因子小波变换和重叠簇收缩基本理论
1.1 可调品质因子小波变换(TQWT)
1.1.1 TQWT 基本原理
TQWT通过设置品质因子来实现小波基振荡特性可调化,有效地弥补了离散小波变换存在的不足。与传统方法相比,TQWT在概念上更为简单,操作也更加灵活。
图1为TQWT的滤波器结构示意图,其中具体的低、高通尺度伸缩所对应的尺度参数α和β分别见图2(a)和图2(b)。假设原始输入离散信号的采样频率为fs,则对于TQWT中的低通滤波通道,其输出信号的采样频率为αfs;而对于高通滤波通道,输出的采样频率则为βfs。
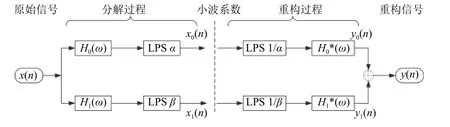
图1 TQWT 滤波器结构示意Fig. 1 Block diagram of filter banks for the implementing TQWT
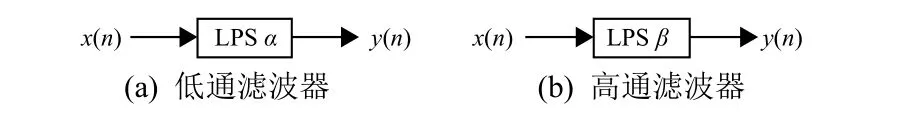
图2 TQWT 低、高通尺度伸缩滤波器示意Fig. 2 Block diagram of scalable low-pass and high-pass filters in the TQWT
尺度参数α和β与控制参数Q、r的关系为
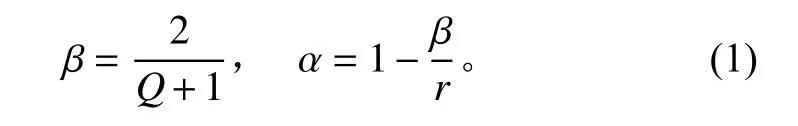
1.1.2 TQWT 的滤波器组设计
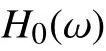
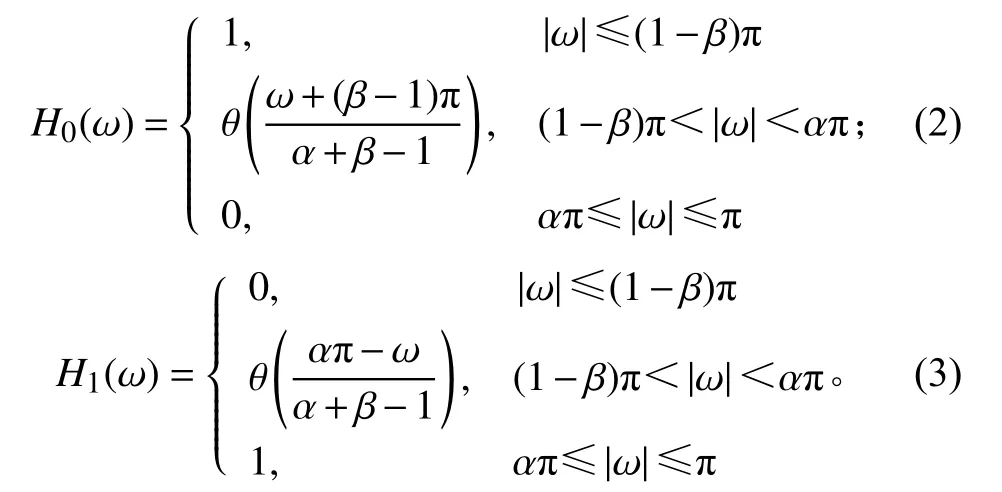
其中,
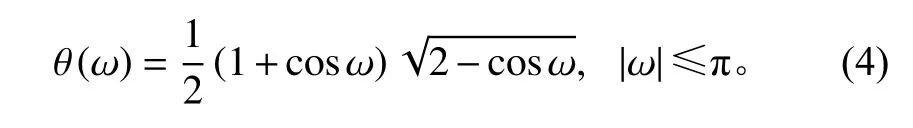
1.1.3 TQWT 参数设置
品质因子Q、冗余度r和分解层数J为可调品质因子小波变换的主要参数。其中:Q(Q≥1)是小波基振荡特性的控制参数,高品质因子的TQWT对应的小波基的振荡次数较多,而低品质因子的TQWT对应的小波基的振荡次数则较少;r是指变换的总过采样率;J定义了小波变换的阶数,TQWT是由双通道滤波器组序列组成,每个滤波器组的低通输出作为输入到后续的过滤器组,而参数J为过滤器组的数量。图3为TQWT小波函数在2组不同参数下的波形及频率响应。
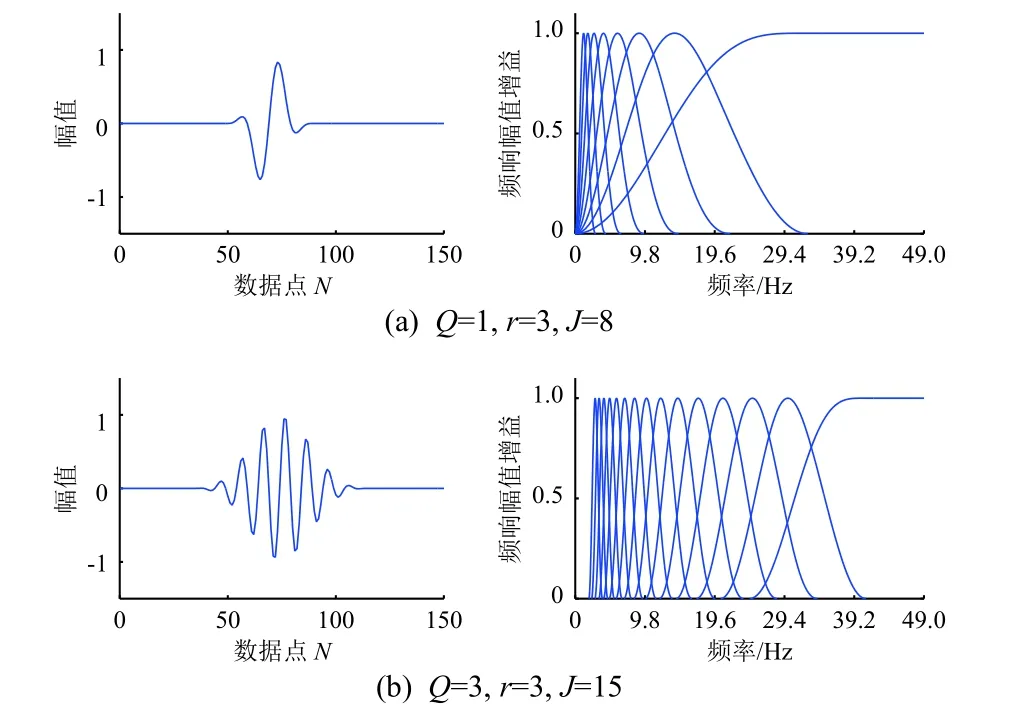
图3 TQWT小波函数在2组不同参数下的波形及频率响应Fig. 3 TQWT wavelets and frequency responses for two sets of factors
1.2 重叠簇收缩 (OGS)算法
本文研究磁异常信号微弱特征的提取问题,假设观测到的含噪信号y可表示为
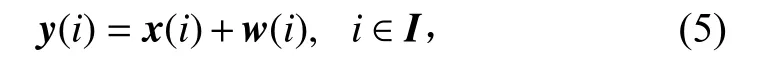
其中:x(i)表示具有簇稀疏特性的信号;w(i)表示背景噪声,一般为高斯白噪声。由于信号具有簇稀疏特性,故将信号x视为一个整体,范数和范数相结合可得到如下惩罚函数:
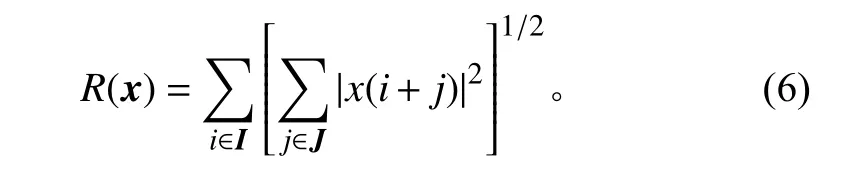
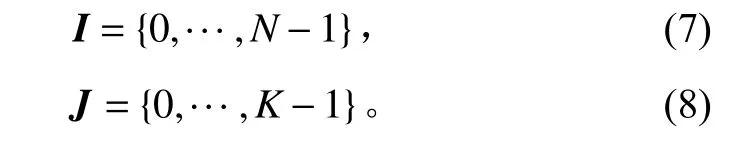
因此,该问题的目标函数可构造为
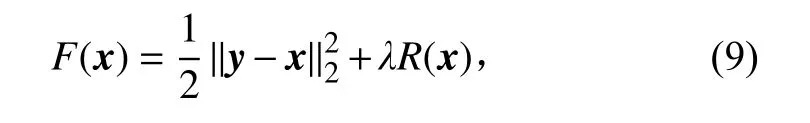
其中,λ为正则化参数。
对式(9)中的x(i)进行一阶求导,可得其最优解:
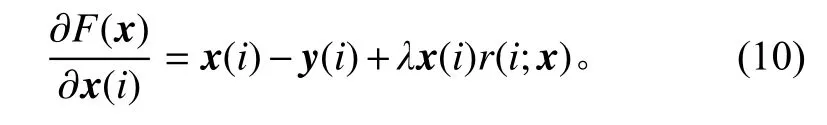
其中,
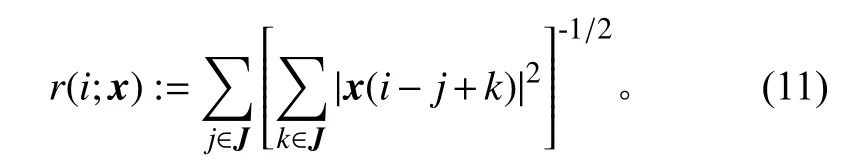
令式(10)等于0,则有
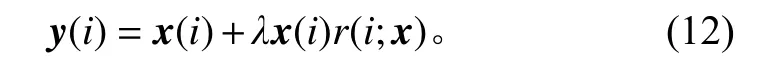
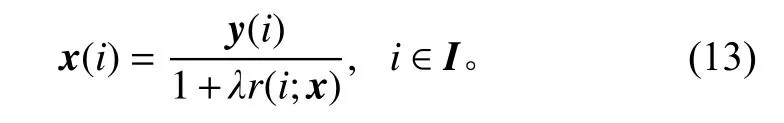
这一连续迭代的方法就是重叠簇收缩(OGS)算法,以此来求出目标函数式(9)的最优解。OGS算法的参数主要包括:正则化参数λ、簇的大小M以及迭代次数Nit。由于OGS算法具有严格的凸性,所以其最优解唯一。
1.3 峭度指标
峭度K(Kurtosis)是信号分析与特征提取中的重要统计指标之一,反映了信号分布特点[9-10]。K对较大值的数据特别灵敏,容易捕捉到探测信号中的瞬态冲击信息。峭度的定义为
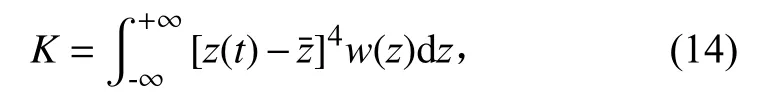
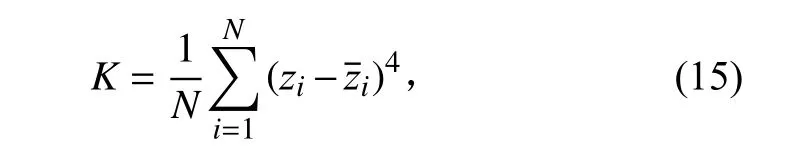
式中N为采样长度。
当信号中存在较大的脉冲时,常采用峭度指标KV作为特征导引指标,

其中σ为标准差。
2 磁异常信号的小波域稀疏优化特征提取算法
本文针对复杂背景下磁异常信号微弱特征提取难题,结合目标特征提取的TQWT和OGS算法,提出了一种基于OGS的TQWT簇稀疏特征提取方法,建立目标函数
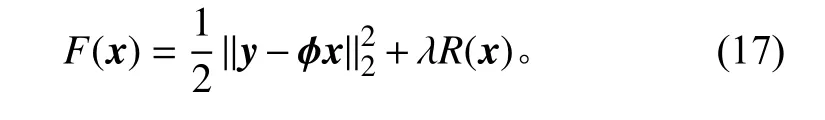
该算法的详细流程如图4所示,具体步骤如下:
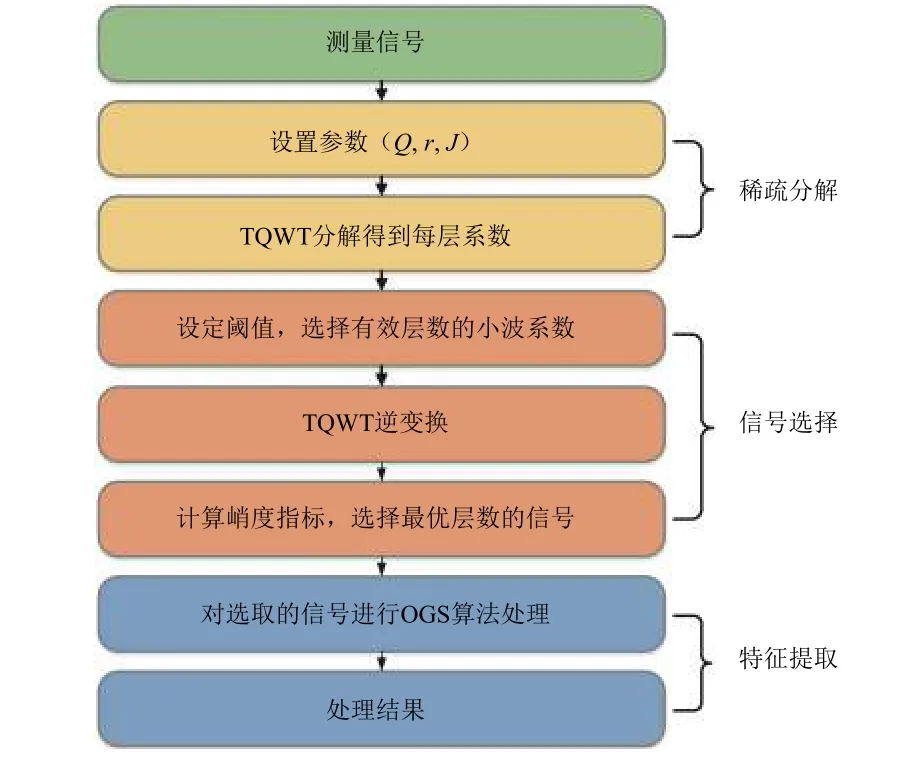
图4 基于 OGS 的 TQWT 算法流程Fig. 4 Flowchart of the TQWT algorithm based on OGS
1)设置参数(Q、r、 J),利用可调品质因子小波变换对测量信号进行分解,得到详细系数以及每层系数所占的能量比。
2)第一次层级筛选。针对能量百分比设定阈值,认为超过阈值的能量为有效能量,去除无效小波系数。
3)第二次层级筛选。对有效能量所对应层级的小波系数进行TQWT逆变换,采用峭度指标分别对其进行计算,并选取最优层级的信号。
4)运用OGS算法对选取的信号进行收缩降噪处理。
3 工程验证
近年来,随着地磁场探测技术的大幅提升与广泛应用,对磁性运动目标产生磁异常信号的探测已成为目标识别的研究热点[11]。然而,在对此目标进行测量过程中,磁异常数据很容易受到外界各种干扰影响。因此,对于高精度的测量来说,有效地消除数据中的噪声就十分关键。
当前,磁异常探测的常用方法主要分为标量方法和矢量方法。与标量相比,矢量方法的信息采集能力更强,是目前磁异常探测领域的主流方法[12]。为了验证本文所研究方法的有效性,将其应用于海洋磁场某矢量磁力仪的观测数据处理,采样频率为250 Hz。该观测数据是由目标信号以不同磁矩大小沿着不同航迹匀速通过探测器附近所得到。选用方均根误差(root-mean-square error, RMSE)和信噪比(signal-noise ratio, SNR)[13]对提取结果进行性能评估。
图5(a)为海洋磁场中目标信号的仿真,图5(b)为采用海洋磁场某矢量磁力仪对目标进行观测得到的数据。从图5(b)可以看出,信号中包含大量噪声且具有极低频的趋势项,各种干扰使得测量得到的数据与原目标信号波形相比存在严重失真,其RMSE=1.792 2、SNR=-18.689 8 dB。采用可调品质因子小波变换对该信号进行29层分解,其中参数设为Q=1、r=3、J=28,得到每层子带的小波系数波形以及小波系数的能量百分比,结果如图6所示。
对每层小波系数进行TQWT逆变换后,分别进行峭度指标计算,得到每层信号的峭度指标值。由于在图6中可以发现,在19层以前,小波系数的能量几乎为0,所包含的信号信息可忽略不计,故在之后根据峭度指标选取层级时不考虑这些层级;在19至29层中,根据峭度指标最大值原则,选取19至21层为最优层级。图7为峭度指标计算结果。
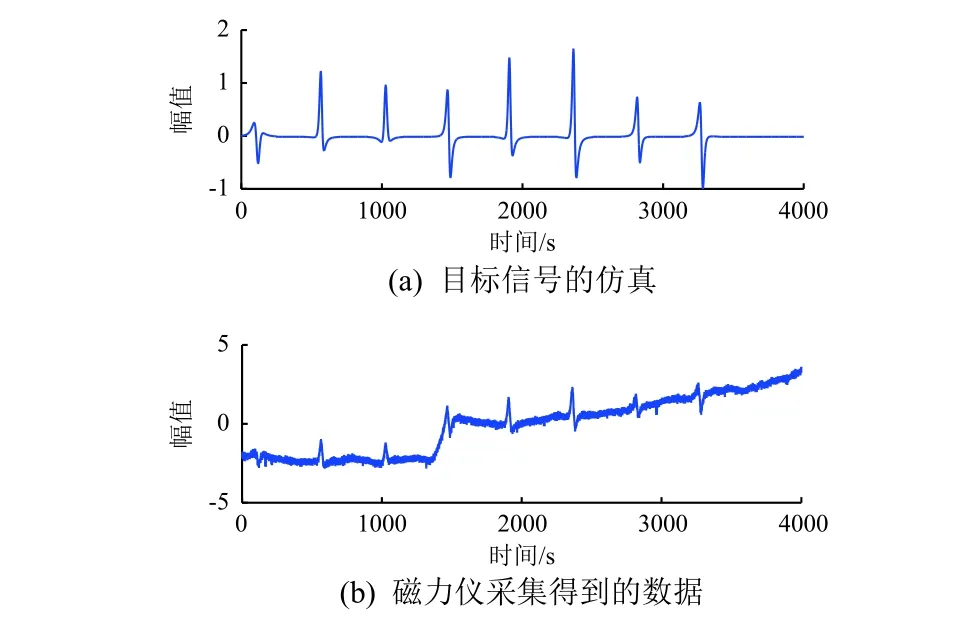
图5 目标信号仿真结果与实测磁信号数据Fig. 5 The simulated signal and the measured magnetic signal
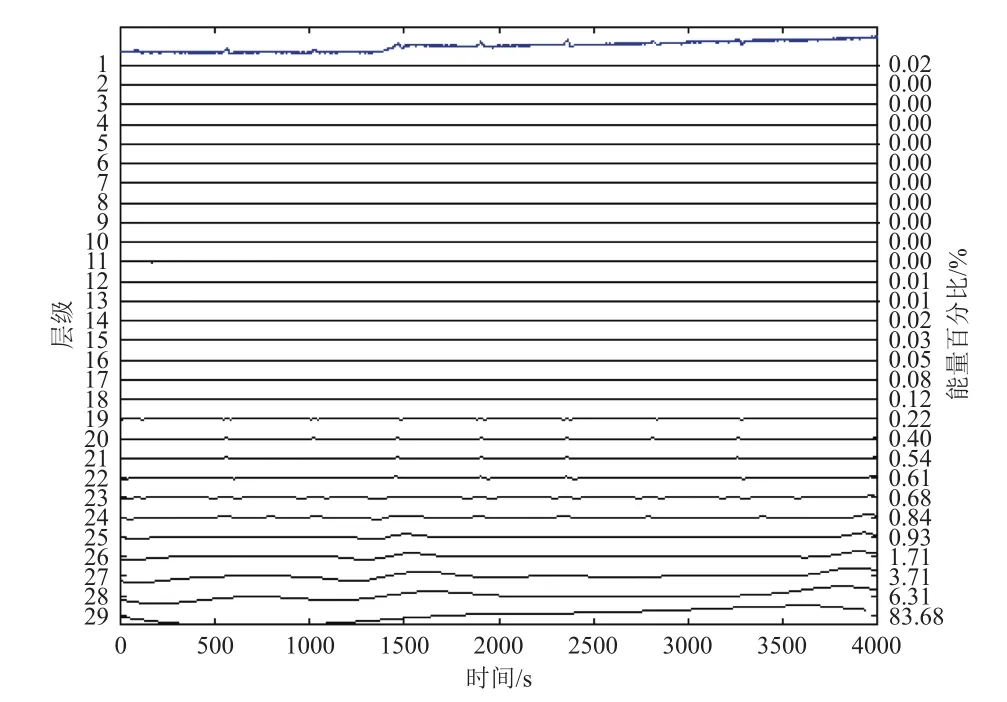
图6 TQWT 分解后每层波形及其能量Fig. 6 Wave and energy for each subband in percentages of the total energy
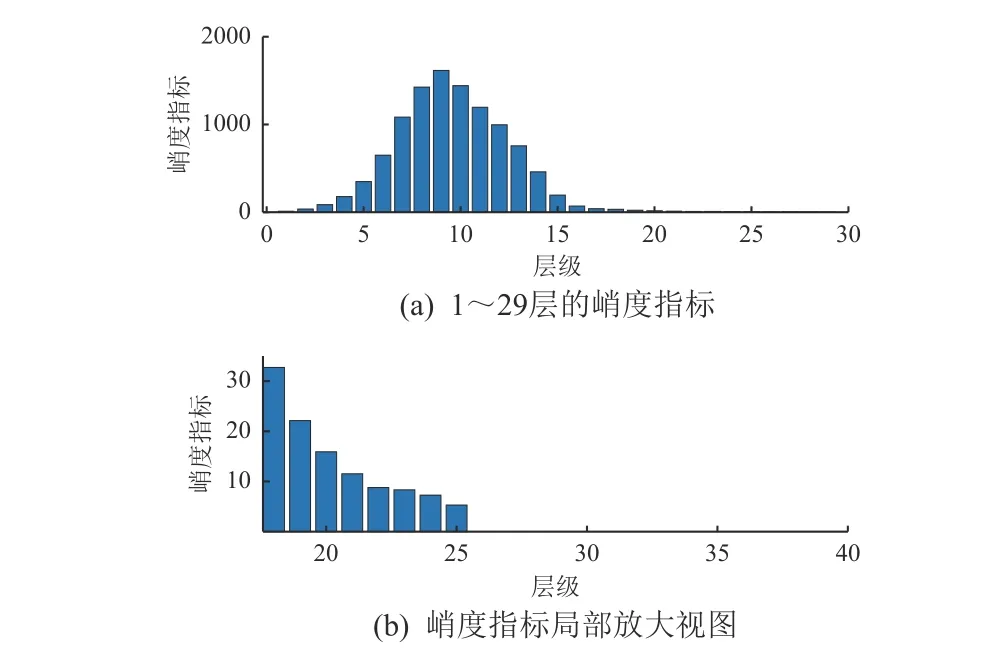
图7 小波子波带重构信号的峭度指标计算结果Fig. 7 The kurtosis values of the reconstructed signal from the single subband wavelet
对所选取的19~21层进行TWQT逆变换,得到重构结果如图8所示。可以看出,由TQWT基本提取出了所需要的目标信号,但仍存在部分噪声干扰。由于该信号具有簇特性,故可采用OGS方法进一步进行特征信号提取。根据信号的特性,将簇的大小M设置为5,正则化参数λ设为0.009 5,迭代次数Nit设为100,处理结果如图9所示,其RMSE=0.141 8、SNR=3.342 1 dB。
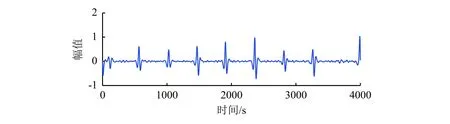
图8 19~21 层小波系数重构结果Fig. 8 Signal reconstruction by the wavelet coefficient for 19 to 21 layers
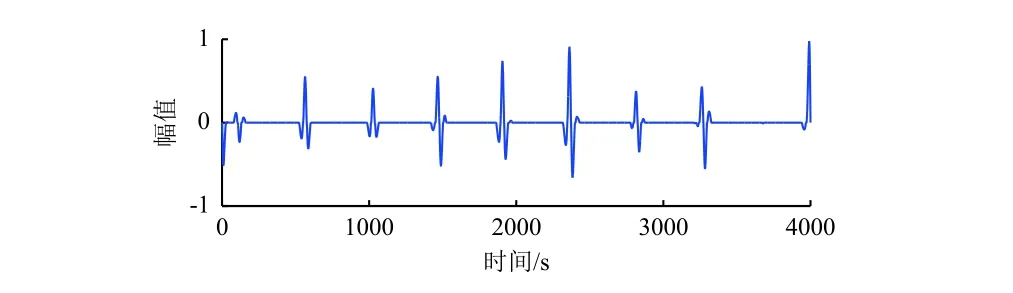
图9 采用 OGS 进一步降噪处理结果Fig. 9 The denoised result by the OGS algorithm
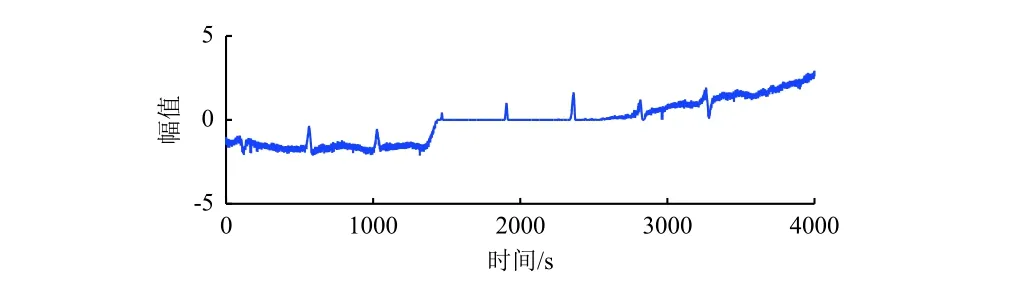
图10 仅采用 OGS 进行降噪处理结果Fig. 10 The denoised result using only the OGS algorithm
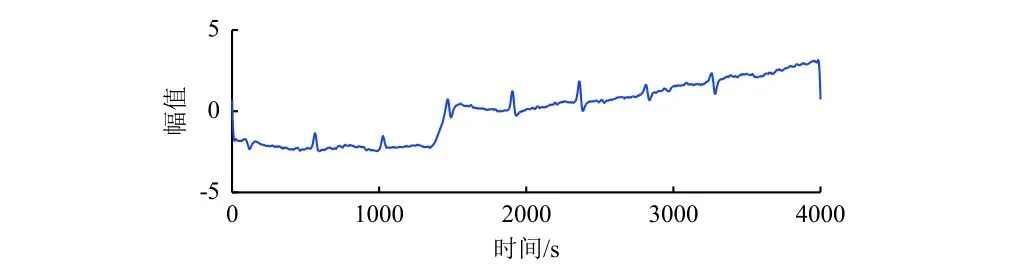
图11 采用范数进行降噪处理结果Fig. 11 The denoised result by the norm
对比本文提出的方法,采用以上两种方法仅提取出少量特征信号,且提取出的信号较原目标信号波形仍严重失真,而本文方法可以极大限度地消除背景噪声的干扰,更为精确地提取出有用特征信号。
4 结束语
为有效地从含噪信号中提取磁异常信号特征波形,本文提出了基于重叠簇收缩的可调品质因子小波域稀疏特征提取方法——重叠簇收缩(OGS)算法,其能够快速求解,并收敛于全局最优解。将该方法应用于海洋磁场目标信号特征提取中,通过方均根误差和信噪比指标定量分析其有效性,进一步验证了该方法在微弱特征提取中表现优越。
