采煤机截割减速机典型故障特征的研究

高大伟， 梁宝林， 李 军

（1.霍州煤电集团安全监察局， 山西 临汾 031400； 2.霍州煤电集团吕梁山煤电公司方山县店坪煤矿，山西 吕梁 033100）

引言

采煤机工作环境恶劣，并且工作过程中受到的动载荷较大，因此出现故障的几率较高。据统计，采煤机传动系统故障率相对较高，其中80%的故障是由于齿轮引起的，可见齿轮故障是采煤机产生故障的重要因素之一[1-3]。因此，对传动系统中各齿轮箱的故障诊断进行研究，准确提取各故障的典型特征，及时诊断齿轮箱故障原因就显得尤为重要。

1 采煤机截割减速器结构

采煤机截割减速器结构如图1所示，通过中间减速器将扭矩传递至小锥齿轮Z1，带动大锥齿轮Z2转动，然后通过大锥齿轮轴将扭矩传递给左右两侧的行星减速系统，最终通过行星架传递至采煤机的切割滚筒，旋转扭矩带动截割齿完成对煤层的截割。从上述传递过程可以看出大小锥齿轮作为扭矩输入与输出的转换部分，对采煤机截割部的性能具有重要影响。

2 齿轮系统振动机理分析

2.1 齿轮系统模型简化

齿轮传递系统具有高耦合、非线性、高阶的特点，因此在齿轮对啮合模型建立的过程中需要对模型进行合理的简化。常见的齿轮分析过程中将齿轮副啮合过程简化为一组包含有质量、阻尼和弹簧的振动系统[4]，具体简化模型如图2所示。

根据上述模型，建立齿轮副振动方程[5]：

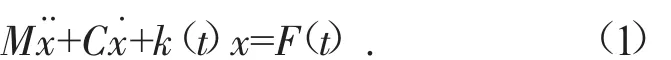
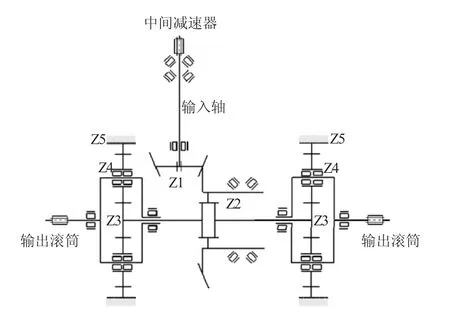
图1 采煤机截割减速机示意图

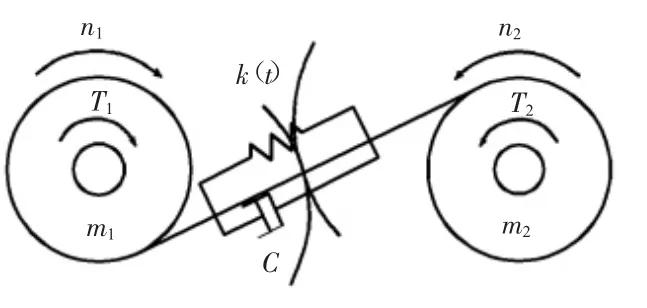
图2 齿轮啮合振动模型

式中：M为齿轮副的等效质量，其表达式为M=m1·m2/（m1+m2），m1、m2分别为啮合齿轮对的质量；x为由于啮合两齿轮制造误差等原因造成啮合齿对在啮合线上的相对滑移量；若齿轮1和齿轮2的位移分别为x1、x2，则x=x2-x1。C为齿轮对啮合阻尼；k（t）为齿轮对啮合刚度；F（t）为齿轮系统所受的外部激励载荷，即激振函数；一般将系统所受激振力用下式表示：

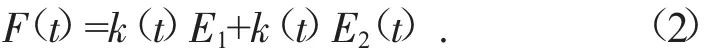
从齿轮外部激励表达式可以看出，该作用力主要包括两部分，其中E1为齿轮所受静弹性变形的平均值，该部分为齿轮固有特性，与齿轮制造误差和故障无关；k（t）E2（t）主要反映齿轮故障与变频之间的关系，受齿轮故障和啮合刚度的影响。因此，被称为齿轮故障函数。

根据齿轮啮合原理可以知道，齿轮啮合过程中会有单对齿啮合、两对齿啮合交替出现的现象，因此会对齿轮形成周期性的冲击力，造成齿轮的啮合振动。其谐频和啮合频率的计算公式分别如下：

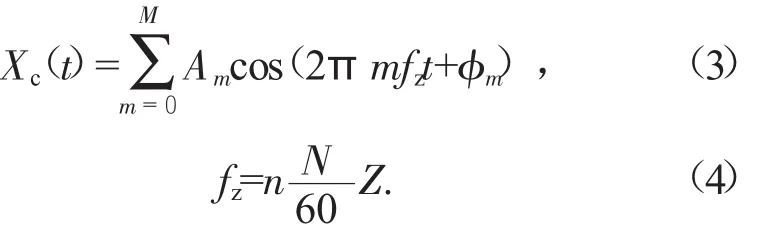
式中：Xc（t）为齿轮的振动时域信号，mm；Am为第m阶啮合频率谐波分量的幅值，mm；m为调幅系数；φm为第m阶啮合频率谐波分量的相位，rad；fz为齿轮的啮合频率，Hz；n为自然数 1，2，3，...，M，M为最大谐波次数；N为齿轮工作转速，r/min；Z为齿轮齿数。

2.2 齿轮的啮合刚度

齿轮啮合刚度值是研究齿轮动态特性的一个重要参数，其主要受到齿轮变形、啮合位置、载荷分布等因素的影响。由于齿轮啮合具有周期性特点，齿轮啮合刚度也是周期变量，图3中分别为直齿轮和斜齿轮啮合刚度变化曲线，从图可以看出直齿轮啮合刚度变化具有跳跃性，变化较为陡峭，斜齿轮啮合刚度变化较为缓和，类似正弦变化[6]。

图3 齿轮啮合刚度变化曲线

齿轮副在啮合过程中，从一个齿进入啮合状态到下一个齿进入啮合，这个时间段中齿轮的啮合刚度就发生依次变化，由此可以计算出齿轮的啮合周期以及啮合频率。假若齿轮副中主动轮和从动轮的转速分别为n1、n2；齿数分别为z1、z2，则齿轮啮合刚度k（t）的变化频率及谐频为：

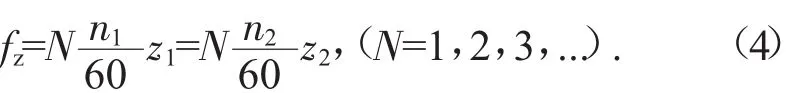
式中：当N=1时，为啮合刚度的变化频率；N≥2时，为其谐频。从式（4）中可以看出齿轮啮合过程中，不论齿轮是否存在故障，其振动信号中均有啮合频率和谐波成分的存在。但是齿轮在处于正常和故障两种不同状态下其振动水平有着明显差异，这就为通过齿轮啮合频率分量进行故障诊断提供了理论依据。

3 仿真分析

通过Pro/E对减速器进行实体建模和装配，然后将实体模型导入到ADAMS中进行动力学分析，建立的仿真模型如图4所示。建模过程中，大小锥齿轮各主要参数为：大锥齿轮齿数z1=30，小锥齿轮齿数z2=20，锥齿轮平均模数m=10，输入轴转速n=180 r/min，两齿轮间的接触刚度系数为K=11.67×105N/mm，杨氏模量E=2.07×105N/mm，负载扭矩为2.5×107N·mm，通过添加相应的约束、载荷、驱动和接触力，对上述模型进行动力学仿真分析。

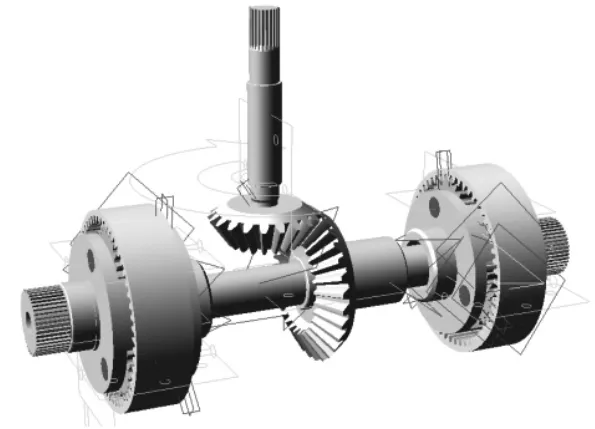
图4 采煤机截割减速机仿真模型

针对上述仿真模型，本文重点对大锥齿轮发生断齿故障、严重齿形误差故障时的运行工况进行动力学仿真，并将仿真数据导入MATLAB中进行时域和频域分析。

图5所示为大锥齿轮发生断齿故障时齿轮对啮合力的时域图，从图中可以看出故障齿轮会对齿轮对形成周期性的冲击，冲击载荷的频率与齿轮理论转频2 Hz接近，并且该冲击载荷对齿轮啮合力形成较大影响，使得啮合力幅值形成较大波动。另外，随着故障严重程度的加大，冲击幅值也增大；从图6所示的频域图可以看出，发生断齿故障后，频域图中分别在61.66 Hz、123 Hz、184.3 Hz、245.7 Hz、307 Hz 处出现幅值突变，该系列频率值与故障齿轮的理论啮合频率60 Hz以及高次谐波非常接近，并且在频率为123 Hz处幅值最大，两侧出现了高而宽的调制边频。

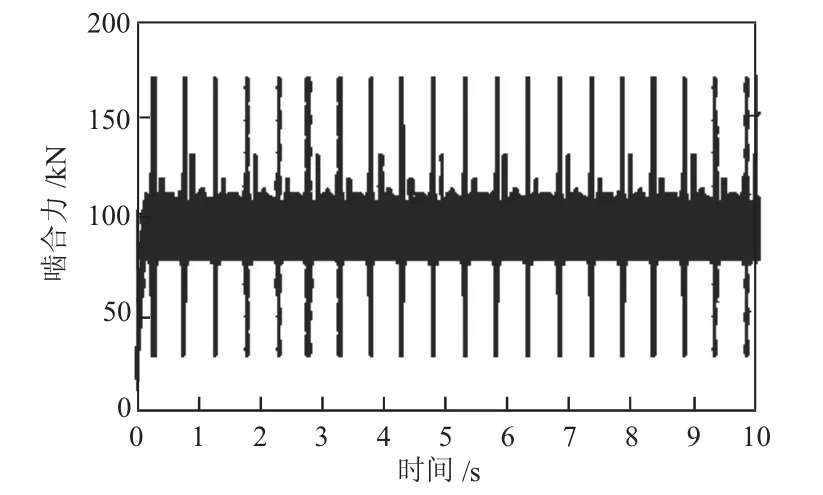
图5 锥齿轮对啮合时域图（断齿故障）

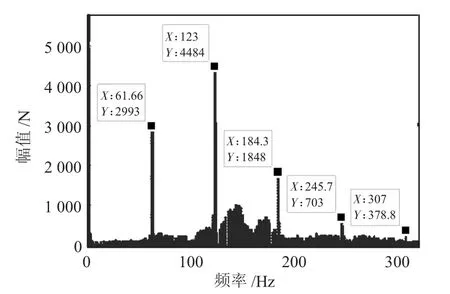
图6 锥齿轮对啮合频域图（断齿故障）

图7所示为发生严重齿形误差故障时齿轮对啮合力的时域图，从图中可以看出故障齿轮会对齿轮对的正常啮合力形成周期性冲击，冲击载荷频率与齿轮理论转频2 Hz接近，并且随着齿形误差的加大，冲击力幅值增大；从图8所示的频域图可以看出，发生齿形误差故障后，频域图中分别在59.58 Hz、121.3 Hz、182.4 Hz处出现幅值突变，该系列频率值与故障齿轮的理论啮合平率60 Hz以及高次谐波非常接近。在频率为121.3 Hz处幅值较大，在其两侧出现了窄而小的调制边频。

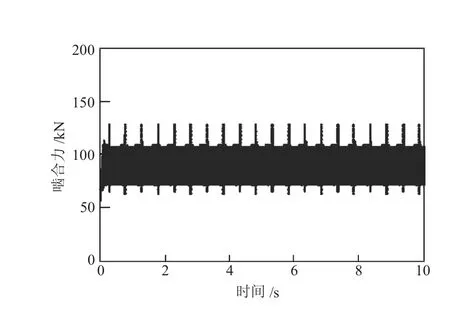
图7 锥齿轮对啮合时域图（齿形误差故障）

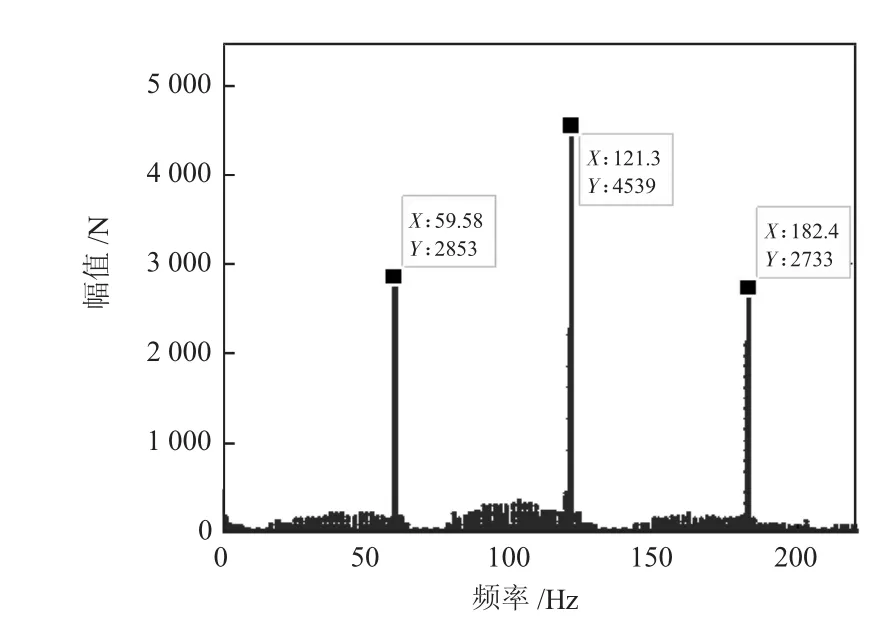
图8 锥齿轮对啮合频域图（齿形误差故障）

4 结论

通过设置断齿故障和齿形误差故障来研究齿轮传动典型故障特征，对含有故障的振动信号分别进行时域和频域分析，结果表明：

1）故障齿轮会对齿轮对形成周期性的冲击，冲击载荷的频率与齿轮理论转频2 Hz接近，并且随着故障严重程度的加大，冲击幅值也增大。

2）从频域图可以看出，发生故障后，频域图中出现幅值突变，该系列频率值与故障齿轮的理论啮合频率60 Hz以及高次谐波接近。整体上断齿故障对齿轮对的冲击要比齿形误差大。

3）频谱幅值最大处，断齿故障主要以高而宽的调制边频为主，齿形误差故障主要以窄而小的调制边频为主。