关于SGB4318型刮板输送机驱动链轮的仿真与优化

张俊杰

（霍州煤电集团吕梁山煤电有限公司木瓜煤矿， 山西 方山 033100）

引言

刮板输送机是煤矿开采中一种常用的装备，其对物料的转运，提高生产效率起着重要的作用。随着开采行业的不断发展，刮板输送机也不断朝着大型化、自动化、智能化方向发展，对于提升煤矿产能发挥了重要作用。但是，刮板输送机本身结构安全问题也受到人们的广泛关注，其链传动驱动轮的结构设计对链条、驱动轮的使用寿命具有极大的影响，研究链轮驱动轮结构优化的问题，对于提高刮板输送机使用寿命、提升煤矿开采企业整体效益具有重要意义。本文对SGB4318型刮板输送机驱动轮进行结构优化分析，为刮板输送机结构设计提供理论参考[1-3]。

1 常见链轮的失效形式

与齿轮的失效形式相似，刮板输送机驱动轮链轮的主要失效形式包括磨损、齿根断裂、压溃等。磨损在链轮工作中是不可避免的，由于工作环境会产生一些微小固定颗粒掉落在链轮与链条接触的链窝中，在循环载荷的作用下，在轮齿表面形成凹坑。凹坑进一步发展，形成微小裂纹，从而不断扩散，最后导致断裂失效[4]。

链轮齿面压溃失效，通常是由于工作载荷过大，或者是链轮本身结构问题以及加工工艺的处理不当造成的。链轮容易受到由链条传递而来的冲击载荷，很容易导致链轮产生塑性变形，变形之后的形状与原链条的形状并不契合，从而导致齿面压溃。与齿轮结构类似，驱动链轮的结构设计参数包括齿数、节圆直径、分度圆直径、齿宽、齿厚等，链轮的优化从这些设计参数入手[5]。

2 模型的建立

2.1 模型的创建

对链轮与链条拟合状态进行应力分析，首先对SGB4318型刮板输送机关键参数进行说明，其输送量为50 t/h，设计长度为50 m，链条规格为Φ14 mm×150 mm，链速为0.80 m/s。根据链条与链轮仿真分析的应力计算结果，对驱动链轮进行结构优化，驱动链轮主要参数见表1。

在三维软件SolidWorks中创建好链轮与链条的三维模型，以Parasolid文件格式导入ANSYSWorkbench中，并完成两模型之间配合关系的设定[6]。

在ANSYS Workbench中新建一个Structural分析模块，分别设置好链轮与链条的材料各项参数，圆环链的材料是23MnCrNiMo，泊松比为0.25，弹性模量为210 GPa。驱动链轮的材料选择30GrMnTi，弹性模量为206 GPa，泊松比为0.3。模型采用自动划分网格技术，并对两模型相互接触地方的网格进行优化，图1所示为模型网格划分示意图。

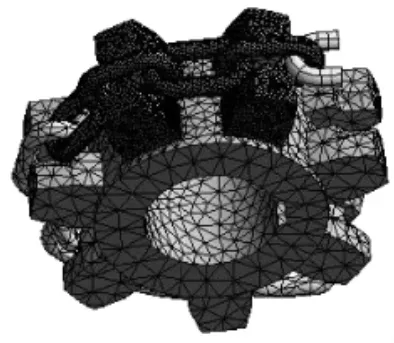
图1 模型网格划分示意图

2.2 载荷与边界条件的确定

首先，在驱动链轮与链条之间，创建摩擦接触，在ANSYS Workbench前处理模型中设置Frictional有摩擦接触，设置动摩擦系数为0.25，静摩擦系数设置为0.2。设置链条的拉力为7.3 kN，固定约束链轮轴孔位置，仿真时间设定为0.2 s，补偿系数设置为2，进而仿真驱动链轮的最大应力及应力分布情况。

3 接触分析结果

根据ANSYS Workbench模型计算仿真结果，得到链轮与链条在啮合过程中应力分布的情况，如图2所示。

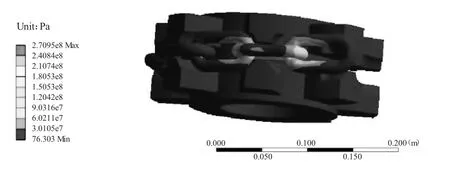
图2 应力分析结果

由图2分析结果，得到当驱动链轮受到链条作用力时，链轮的链窝处应力应变最为明显，也就是链轮与链条刚刚开始拟合的地方。就分布情况来看，链窝底部平面与链窝侧面，与链条啮合接触区域应力分布最大，最大172.3 MPa，其他位置的应力分布较小。

4 链轮的优化设计

对链轮结构优化设计采用的正交优化设计法，是一种典型多因素的试验设计验证方法。其原理是依据正交特性，使用正交表格，从而在较少的试验次数中获得比较理想的优化结果。本文采用正交优化法对链轮的相关重要参数做优化统计，经过仿真分析得到最佳结构参数，从而改进、提升链轮的使用性能。

4.1 优化参数的选择

根据对刮板运行过程中对链轮与链条啮合过程的受力进行分析，确定驱动链轮的链窝为主要承载位置，选择决定链轮轮齿的三个重要参数。建立好相对应的模型，通过仿真分析得到接触应力，由此可以确定各参数对链轮性能的影响。本文中选择齿厚、齿形圆半径、链窝弧半径三种参数来设计优化仿真试验。图3所示为优化参数示意图。

4.2 正交优化结果

为了便于表达，在此用符号a表示齿厚参数，R表示齿形圆弧半径，r表示链窝弧半径，然后取a为44 mm、45 mm、46 mm，R取 23 mm、24 mm、25 mm三个参数，r取28 mm、29 mm、30 mm三个参数。将正交优化分析法所得的序列组合作为优化分析的参数，已知关于a、R和r的参数设计如表2，以这九种模型设计正交优化试验方案，并得到试验结果，如表2所示。

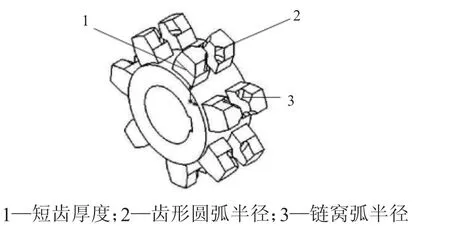
图3 优化参数示意图

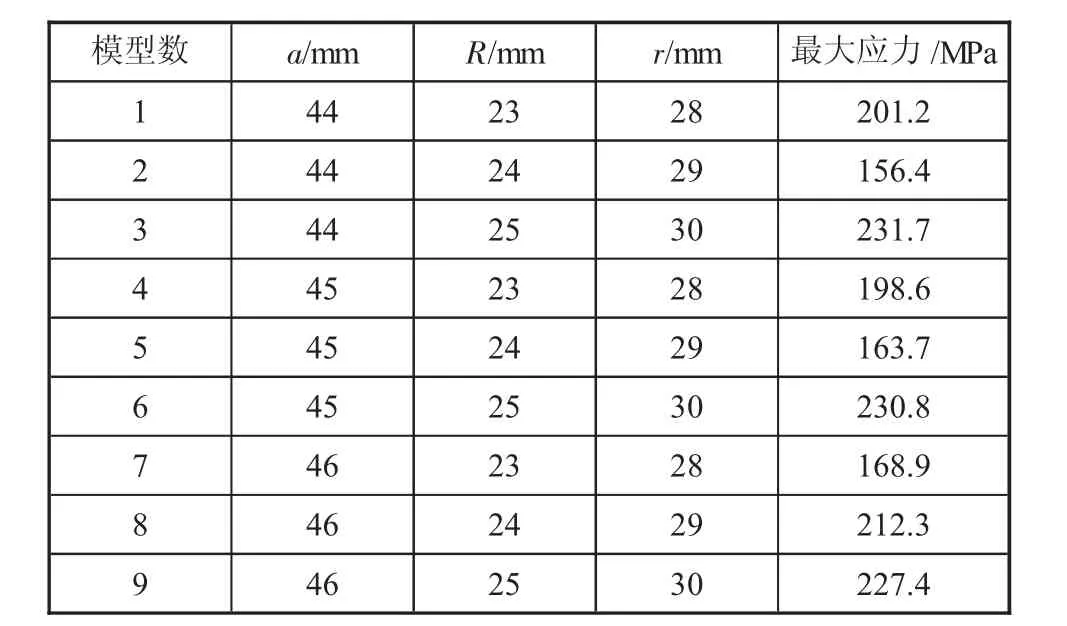
表2 正交试验分析结果

然后使用方差分析的方式处理试验结果，在直观分析中，发现因素R、r，即齿形圆弧半径、链窝弧半径在分析结果中，对链轮应力分布影响更大，在对试验结果进行方差分析时，只考虑R与r，两个参数为方差设计变量，由于篇幅所限，具体计算过程不再一一展示，最终得到的链轮优化参数为：a=45 mm；R=30 mm；r=24.2 mm。据此重新建立链轮与链条的接触模型，导入ANSYS Workbench，对模型进行网格划分、材料参数设置、接触设置等，分析计算优化后的应力计算结果，齿轮应力结果如图4所示。

图4 优化后链轮的接触仿真

在相同的边界条件、载荷设定的情况下，优化后链轮接触分析最大应力为160.5 MPa，最大应变值为0.001 21 mm，与优化前原始状态计算结果对比，如表3所示。

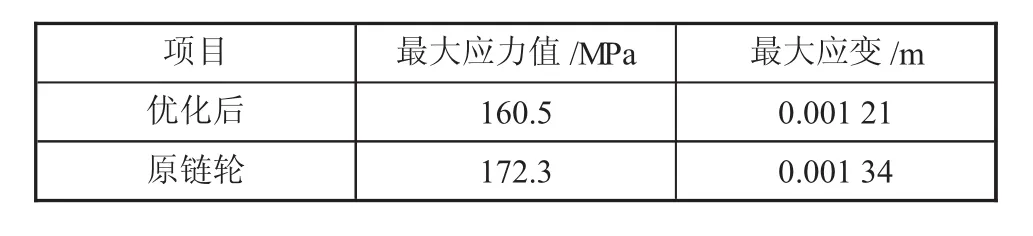
表3 漏电保护测试数据

由表3可知，优化后最大应力减小了6.84%，最大应变减少了9.61%，对链轮结构参数的设计改进效果明显，优化方案是针对链轮的设计参数改进的，所以对驱动链轮的结构设计具有参考意义。

5 结论

1）对影响链轮接触应力的三个因素作为变量建模求解。对九个试验分析模型进行分析，选择了两个影响最大的因素，并确定相对最优的链轮优化参数为a=45 mm、R=30 mm、r=24.2 mm。

2）优化后最大接触应力减小了6.84%，最大应变减少了9.61%，对链轮结构参数的设计改进效果明显，为链轮的优化设计提供了理论指导，为提高链轮可靠性以及输送机整体的生产效益具有重要意义。