利用双线性应力-应变模型求解管道爆裂压力

杜改平

（太原锅炉集团， 山西 太原 030008）

引言

解析解在力学的各个领域都有价值，为数值模拟程序的建立以及实验程序和装置的校准提供了基础。当解析解不能用数学方法描述时，可以使用数值模型或实验测量等基本方案解决。如在缺口效应区域，存在平板中圆形或椭圆形孔的应力分布状态的解[1]。数值模拟求解了较为复杂的切口形状的解析解。在压力容器领域中，对于承受内部压力的圆柱形容器有解析解。解在弹性和弹塑性区域都是已知的。在本文中，解析解以弹塑性容器中直至破坏的受压圆柱容器的缩写形式提供，从而可以为使用的双线性材料模型计算爆破压力。腐蚀引起的局部壁厚减薄，可以通过数值模拟来解决，该数值模拟通过具有理想几何形状的压力容器的解析解进行验证。

蒸汽锅炉在目前的生产和应用中使用非常广泛，本文以锅炉汽水管道的变径管道为例，由于锅炉在运行过程中，会产生压力和腐蚀破坏，以往对锅炉管道形变分析通常以热应变进行分析，本文对管道进行数学模型分析和三维应力分析，再进行爆破试验和腐蚀件试验，从而得到一个符合实际情况的结果，对锅炉管道在运行工作状态中起到参考作用，从而减少爆管情况的发生。

1 压力容器的弹塑性应力-应变状态的求解

在锅炉汽水管道中，变径管道通常使用合金钢铸造，连接处采用焊接，在实际运行过程中，由于工质水受热在汽化过程中体积会发生膨胀，从而对管路系统造成一定的冲击，导致管道容易发生一系列形变[2]。因此在弹塑性应力和应变的推导过程中，应考虑到材料的不可压缩（v=0.5）和材料的塑性应变发生在总体积不变的情况，并且材料的体积变化始终是弹性变化的状态。如图1所示，z轴沿容器轴方向定向，r1和r2分别为弹性区域和塑性区域的边界处的半径。

图1 内压作用下圆柱形容器壁单元受力及变形

根据小弹塑性变形理论（均匀各向同性材料的扩展胡克定律），图1为内压作用下圆柱形容器壁单元受力及变形。我们可以将方程写成：

式中：εr为径向应变；εt为切向应变；εz为轴向应变；εi为正应变；σr为径向应力；σt为切向应力；σz为轴向应力；σi为正应力。

正应力强度（有效应力）与应力偏差的第2个不变量有关，如公式（2）所示：

式中：τi为切应力；I2为力矩；Dσ为应力面积；σ1为径向应力；σ2为切向应力；σ3为轴向应力。

选择法向应力的强度，以获得最大张力σ1=σi应变强度（有效应变）由以下公式给出：

式中：Dε为应变面积；ε1为径向应变；ε2为切向应变；ε3为轴向应变。

式中：P0为中心受力；r1为内径；r3为外径；r为中径。

作用于上页图1元件上的平衡方程可写为：

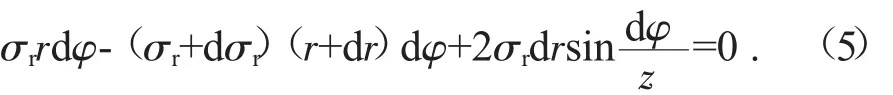
式中：dφ为角度变量；dσr为应力变量；dr为半径变量。

利用式（4）和式（5）求法向力方程：

式中：p1为内部压力；p2为外部压力。

根据式（2）求应力强度：

根据式（3）求应变强度：

式中：u为变形量；du为单位变形量。

消去u，可得到应变的微分方程：

式中：dεt为单位切向应变

通过对式（9）求解，我们得到了以r2为半径的封闭圆柱容器的基本方程：

式中：dεt为单位径向应变；σK为材料应力临界值；r2为形变半径；G为材料剪切模量。

以σi=f（εi）的函数形式计算切向应力和径向应力，图2为拉伸有效解析双线性材料模型。

式中：h为应力比值。

将关系（12）放入等式（11），并应用物理上清晰的边界条件：

可以在弹性塑性区域r1≤r≤r2获得径向和切向应力的关系：

图2 双线性材料模型参数

式中：σrp为塑性区域径向应力；σtp为塑性区域切向应力。

通过方程得到了应力和应变之间的函数关系，作为后文比较依据。

2 爆破压力求解

本节内容将确定压力容器的爆破压力，由于锅炉管道的爆管情况发生较多，本节内容的管道是在没有缺陷的情况下发生爆裂。为了确定爆破压力，必须考虑容器的整个横截面是否处于可塑状态[3]，因为锅炉管道受热产生形变，在发生爆破的同时，管道壁温度较高，管道通常处于可塑状态。可以修改推导方程：

对于双线性材料模型（式12），使用应力强度和应变强度之间的关系，应用塑化时的恒定体积条件（V=0.5）并根据边界条件计算积分常数：

根据Hubert-Mises-Hencky准则可以获得破坏性压力的结果关系：

式中：σred为爆破应力。

同时根据式：

横截面完全可塑化的爆破压力：

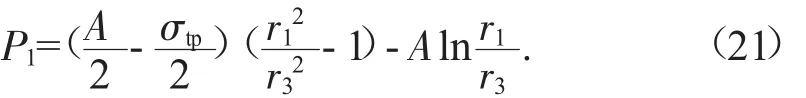
本节得到了压力容器发生过度塑性变形导致爆裂的数学模型，作为下文的比较依据。

3 爆破压力的数值解与实验解对比

利用有限元分析软件ANSYS对管道模型进行数值求解，该软件有较丰富的情况模型和精确的分析结果[4]，首先选择压力容器的尺寸和形状，尺寸采用130 t高压锅炉的主蒸汽下降管尺寸，并且外型存在焊接变径，得到其具体数据使压力容器在实验室条件下也能达到破坏压力。选择圆柱形管道的几何形状，使其在压力下出现的塑性应变发生在中间的锥形部分外底和焊缝区域。

在这个压力容器模型中，实验分别测试了实验管道的几何尺寸（管道缩窄的长度，管道中较粗和较薄部分的长度之比）对变形结果的影响。通过在规定焊接区域的节点的相同位移，分别模拟了容器底部与容器较厚部分之间的焊接效果。通过试验结果表明，焊接作业中所产生焊缝在焊缝质量符合焊接标准的情况下[4]，对压力容器的形变影响很小，对压力容器锥形部分的变形影响不大，可以进行忽略。

对材料进行拉伸破坏实验，材料拉伸曲线（通过直接测量）重新计算的真实应力近似为双线性材料模型，如图3。材料表现出正交各向异性行为，而且在材料的拉伸过程中，切向方向上的抗拉强度比在轴向方向上的抗拉强度高约10%。

图3 用于有限元数值模拟的材料模型

测试压力容器破裂压力的两个试件由150×8管道精车削制成，管道材料为碳素合金钢，试件的尺寸内径为143 mm，壁厚为4 mm，焊接环面底部。实验过程中，首先通过电液脉动仪测得了破坏压力容器试样所需的油压[5]。具体操作时在机架上夹紧直线液压马达（80/50/125），压缩活塞面 5 026.5 mm2，将脉动器施加的力转化为油压。通过实验得到的破坏压力的结果，以及143 mm内径和4 mm壁厚的解析关系的结果，和采用不同的比较准则，以及采用有限元法建立的数值模型的结果如表1所示。

表1 爆破压力结果

根据表1中显示，对于圆柱容器的解析度和数值解的一致性较高，以及与实验模型相对应的密闭圆柱形容器的解析解与数值也有很好的一致性[6]。实验确定的爆破压力值比双线性材料模型的解析解和数值解高出近4%。实验结果表明，与Tresca准则相比，Huber Mises-Hencky准则的选择与现实（对于给定类型的任务和材料）更符合实际情况。

4 有腐蚀缺陷的管子爆裂

采用与之前相同的压力容器试样，模拟管道在腐蚀情况下的爆裂情况。模拟情况主要有模拟面积为41 mm（25 mm宽）、24 mm、35 mm并且壁厚为压力容器75%壁厚且方向是沿容器轴线方向减薄时的破裂压力。所采用的材料模型、有限元模拟程序和爆破压力的实验测量方法与之前的试验和模拟方法相同。表2为通过实验得到的腐蚀缺陷管道试样的破裂压力值。

表2 具有腐蚀缺陷的管道试样破裂压力的比较 MPa

最高的爆破压力是通过实验获得的真实压力。因此可以认为，用数学模型或者有限元分析得到的压力可以进行参考依据，并且存在一定的安全裕量。计算标准使用H-M-H分别以6.5%、10%和11%准则的数值计算最接近这些真实值（使用Tresca准则与实验值相比，破坏性压力值的差异显著）[7-8]。根据标准的关系计算得出的爆破压力值相差20%以上（标准DNV-RP-F101），相差30%以上（ASME B31G标准）。

根据ASME（美国机械工程师协会）标准（DNV）所获得的相对较高的破裂压力。然而，在数值模型中，所有的因素都可以被考虑进去，以确定更接近其真实值的破坏性压力。因此，数值模型是一种很好的工具，可以合法地帮助延长受损管段的使用寿命，从而建立更现实的安全价值[9]，防止破坏这些管段。通过本次试验和分析可以对锅炉的汽水管路进行预处理或者尺寸处理，保证其在运行中的安全。