基于单纯形-最短路径射线追踪的微震震源混合定位算法

王 辉，梁 苗，朱梦博

(1.鄂尔多斯职业学院，内蒙古 鄂尔多斯 017000；2.鄂尔多斯生态环境职业学院，内蒙古 鄂尔多斯 017000；3.煤炭科学研究总院，北京 100013)

近20年来，随着我国经济快速发展，深部矿产资源开采、深埋隧洞开挖、高陡边坡治理等岩土工程活动进入井喷阶段，由此促进了微震监测技术的研究与应用。震源定位是微震监测技术的基础工作之一，定位的准确性直接影响后续的各种分析工作[1-3]。围绕震源高精度定位问题，国内外学者提出了众多定位方法，包括Geiger法、单纯形法、网格搜索法、粒子群法和相对位置法等传统方法。基于上述经典算法，近几年来国内学者提出了大量的改进方法，包括混合定位方法[4]、基于到时质量控制的定位方法[2,5]、基于观测系统优化的定位方法[6-8]等。这些改进后的方法较好地解决了传统定位方法存在的计算效率低、精度不高、容易陷入局部最优解等问题，但是这些方法仍然基于均匀速度假设。当前，复杂岩土工程对震源定位精度提出了更高的要求，同时监测区域越来越大，地质条件越来越复杂，因此基于均匀速度模型的微震震源定位方法应用效果较差，迫切需要开展复杂速度模型下的震源高精度定位方法研究。

针对复杂速度模型下的震源定位问题，目前主要是通过模拟地震波传播路径来计算地震波走时场，主要应用于天然地震震源定位和地震勘探领域。近几年来，随着地震波射线追踪相关理论被引入到微震监测领域及计算机性能的提高，部分研究人员开始研究复杂速度模型下的微震震源定位问题。郭超等[9]基于FSM算法及到时差数据库技术研究了层状介质下震源高精度定位方法，并将该方法应用于宁武盆地武2-2井水力压裂工程。郭亮等[10]针对实际工程中带有空洞和速度分区等复杂速度模型，通过对FMM进行改进，提出了用于计算地震波走时场的MSFM算法，并将之应用与白鹤滩水电站左岸边坡微震定位。本研究基于地震波传播原理，采用最短路径法计算了地震波射线追踪路径，并计算到时场；然后基于观测系统到时场数据库和单纯形(Simplex)定位方法，建立了单纯形-最短路径射线追踪定位算法。

1 地震波传播原理概述

1.1 费马原理

费马基于光传播路径的研究成果总结提出了费马原理。对于地震波传播问题，费马原理的通俗表述为：地震波沿垂直于波前面的路径(波的射线方向)传播所需的时间最短。 费马原理从运动学的角度描述了波的射线传播特征，由该原理可以推导出波的直线传播定律、反射定律和折射定律(斯奈尔定律)。

1.2 惠更斯原理

惠更斯原理是指波在介质中传播到的每一个点都可以视为一个新的波源，即子波源；每个子波源以所在位置处的速度向各个方向传播微弱的子波。基于惠更斯原理，可以根据当前波前计算一定时间间隔后的波前。如图1所示二维平面，S0为t0时刻的波前，分析S0波前上的4个子波源R1、R2、R3和R4，子波源从t0时刻开始向外传播子波，Δt时间后，各子波面为一个半径为V*Δt(V为波速)的圆，4个子波面的包络面即为t0+Δt时刻的近似波前S1，加密子波源即可得到精度更高的波前S1。

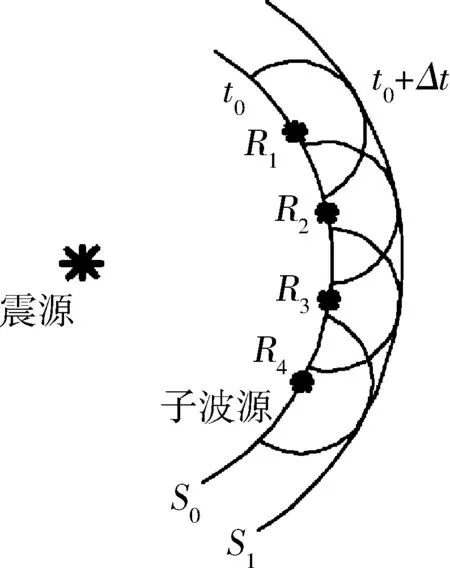
图1 地震波波前扩展原理Fig.1 Seismic wavefront propagation principle

2 最短路径射线追踪方法

最短路径射线追踪方法的理论基础是费马原理和惠更斯原理，具体利用Dijkstra最短路径算法进行实现。最短路径射线追踪算法流程如图2所示，各步骤作用及实现方法如下所述。步骤1：根据监测区域大小及设置的网格步长，建立三维网格速度模型；构建两个节点集合A和Q，A为已经计算过走时的节点集合，Q为作过子波源的节点集合；将震源节点初始化到集合A和Q中，将震源节点走时初始化为0，其余节点的走时初始化为无穷大；步骤2：确定与子波源m相连的所有节点集合V，并将相应节点加入到集合A中；步骤3：确定节点集合S(S∈A，且SQ)中节点n到子波源m之间的走时tmn；步骤4：取{tm，tm+tmn}的最小值更新节点n的走时tn，并记录使节点n形成最小旅行时的前一个节点号；步骤5：取节点集合S中走时值最小的节点更新子波源m，并将该节点加入到集合Q中；步骤6：判断集合Q是否包括所有模型节点，若否则执行步骤2～步骤5，若是则完成走时计算；步骤7：根据步骤4中记录的前节点号，推算从源点到接收点的射线路径。若只是计算地震波走时场，不计算射线路径，则无需执行步骤7。

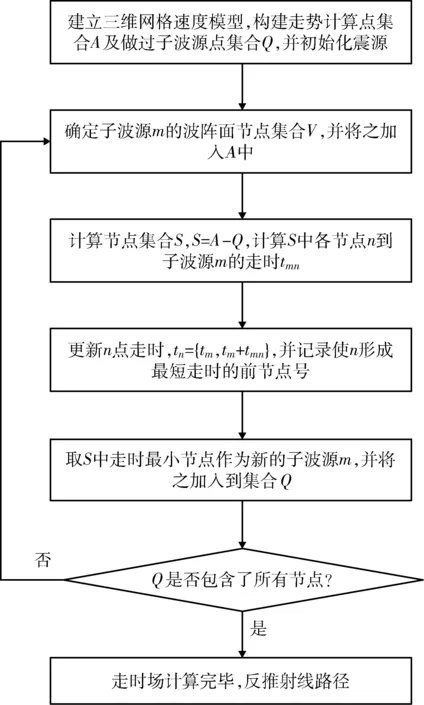
图2 最短路径射线追踪算法流程Fig.2 Shortest path ray tracing flow

需要指出的是，对于三维模型，波源的子波面包括4种情况：①波源在3个边界面交点上，其子波源包含7个节点(图3(a))；②波源在两个边界面交线上(除端部两个节点)，其子波源包含11个节点(图3(b))；③波源在单个边界面的内部，其子波源包含17个节点(图3(c))；④波源在模型内部，其子波源包含26个节点(图3(d))。

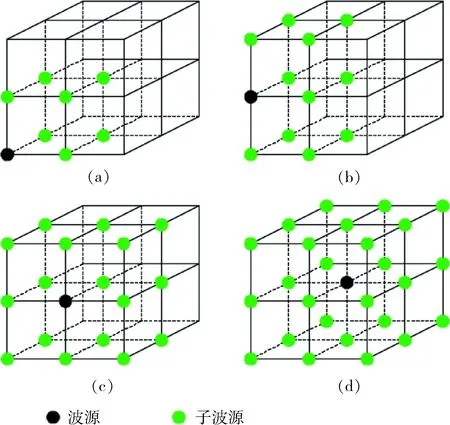
图3 三维模型下波源与子波面空间关系Fig.3 Spatial relationship between wave sourceand wavelet surface

3 单纯形-最短路径射线追踪定位算法

3.1 定位原理

对于微震震源定位问题，可以将检波器先视为震源点，模型中其他节点为检波点，采用最短路径射线追踪方法，即可计算出观测系统中每个检波器到任意节点的地震波走时及其射线路径。根据检源互换原理[11-12]，可以得到监测区域内任意潜在震源节点到各检波器的走时及其射线路径，因此震源定位问题就可以转化为以下数学问题：搜索速度模型中满足式(1)的节点，该节点即为震源的近似位置。

i=1,2,…,l;j=1,2,…,m;k=1,2,…,n

(1)

图4 单纯形-最短路径射线追踪定位算法
Fig.4 A new source location algorithm based on simplex and shortest path ray tracing

3.2 定位数值模拟实验

为了论述单纯形-最短路径射线追踪定位算法的具体实施步骤及其优势，本文建立了矿山常见的层状速度模型和带空区速度模型，分别进行了震源定位数值模拟实验，并将计算结果与常规单纯形定位方法的结果进行对比。

3.2.1 层状速度模型

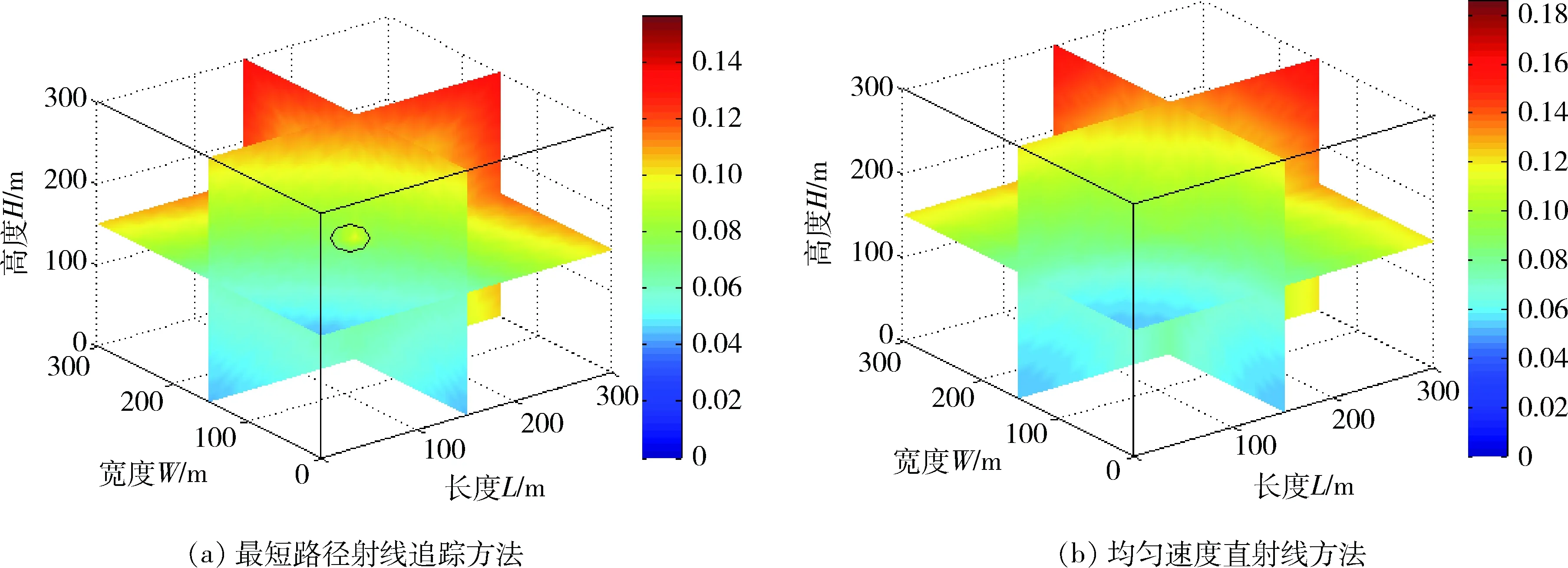
含煤地层是典型的层状速度模型，一般煤层是低速层，顶底板岩层是高速层。建立如图5所示的300 m×300 m×300 m的含煤层状地质模型，设定顶板、煤层和底板的P波波速分别为3 500 m/s、1 500 m/s和3 500 m/s，设定网格步长为5 m，震源点坐标为(0，0，0)。图6为震源点到的射线路径对比图，设定检波点(300，300，300)，其中，灰色虚线为最短路径射线追踪方法正演结果，黑色实线为直射线。由图6可知，最短路径射线追踪方法计算得到的射线路径在波速界面有折射现象，满足斯奈尔定律。图7(a)和图7(b)分别为最短路径射线追踪方法和均匀速度直射线方法计算得到的走时场，其中均匀速度直射线方法中取均匀速度为2 833 m/s。由图7可知，在速度分界面处地震波波阵面形状明显发生改变。

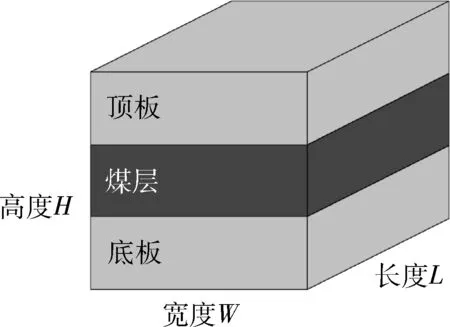
图5 顶板-煤层-底板速度模型Fig.5 Velocity model of roof -coal-floor

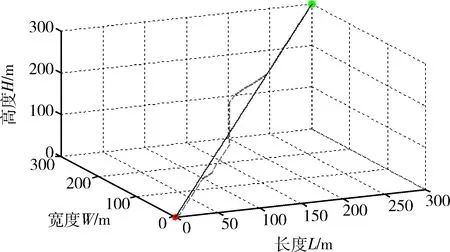
图6 两种方法下震源点到检波点的射线路径Fig.6 Ray paths from source point to detection pointunder two methods

图7 两种方法走时场计算结果(单位：s)Fig.7 Travel-time fields of two methods (Unit:s)

图8 含空区速度模型Fig.8 Velocity model with empty zone

3.2.2 带空区速度模型

微震监测工程中空区速度模型较为常见，包括金属矿的采空区、煤矿的采空区和地下厂房及隧道的开挖区等。建立如图8所示的300 m×300 m×300 m的含空区速度模型，空区范围为{135

图9 两种方法下震源点到检波点的射线路径Fig.9 Ray paths from source point to detectionpoint under two methods

图10 两种方法走时场计算结果(单位：s)Fig.10 Travel-time fields of two methods (Unit：s)

4 工程应用实例分析

本文以神东某矿31101工作面坚硬顶板压裂为例，该工作面直接顶岩性为粉-细砂岩，老顶为致密坚硬的细粒砂岩，厚度为1.2～18.8 m，大部分顶板属于中等冒落～难冒落顶板。此次压裂工程中，采用微震监测技术评价压裂效果，微震观测系统为井地联合方式。监测区下覆地层依次为：黄土层，平均厚度35 m，速度，P波波速1 553 m/s；风化-粗粒砂岩层，平均厚度25 m，P波波速2 931 m/s；细粒砂岩层，平均厚度20 m，P波波速3 374 m/s；泥岩层，平均厚度8 m，P波波速2 693 m/s；粉砂岩层，平均厚度25 m，P波波速3 655 m/s；细粒砂岩层，平均厚度8 m，P波波速3 312 m/s；开采煤层，平均厚度4.8 m，P波波速2 287 m/s。

本次监测过程中，采用放标定炮的方式试验微震监测系统的精度，标定炮震源空间坐标为(8 542.5，2 137.8，482.2)。根据地层信息，按照地层厚度与速度加权方式计算得到平均波速为2 764 m/s。分别采用本文方法和平均速度模型单纯形方法进行标定炮位置定位，与该标定炮位置进行比较，验证本文定位方法的有效性。其中，最短路径射线追踪计算阶段中，设定网格间距5 m。微震观测系统及两种方法下标定炮定位结果如图11所示，表1为标定炮定位误差分析。由图11和表1可知，两种方法均较为准确地定位到标定炮位置，但单纯形-最短路径射线追踪方法精度高很多。 实验表明，本文提出的单纯形-最短路径射线追踪方法能实现震源高精度定位。

图11 微震观测系统及标定炮定位结果Fig.11 Microseismic observation system andblast location results

表1 标定炮定位误差分析Table 1 Location error of two methods

5 结 论

1) 本研究基于检源互换原理，采用三维最短路径射线追踪方法计算了地震波走时场及射线路径，包括常见的层状速度模型和含空区速度模型等两种情况。层状速度模型下，检源路径在波速分界面发生折射；空区速度模型下，检源路径能绕开空区。两个数值模拟实验表明，最短路径射线追踪方法计算得到的走时场及射线路径满足地震波传播的基本规律。

2) 采用最短路径射线追踪方法、单纯形方法建立了针对复杂速度模型下的微震震源定位方法，分两步骤定位微震震源位置。相比于基于走时场的直接搜索方法，新方法计算效率高；相比于基于均匀速度模型的传统单纯形方法，新方法定位精度高。

3) 基于以神东某矿31101工作面坚硬顶板压裂案例，以标定炮为参考，常规单纯形方法定位误差为19.63 m，单纯形-最短路径射线追踪算法定位误差4.35 m，震源定位精度大幅度提高，满足现场需求。