碱性及近中性土壤环境中埋地钢管时变地震易损性分析

谢孝奎，贺金川，郑山锁, ，韩 峰, ，蔡永龙

碱性及近中性土壤环境中埋地钢管时变地震易损性分析

谢孝奎1，贺金川2，郑山锁1, 3，韩 峰1, 3，蔡永龙3

(1. 西安建筑科技大学土木工程学院，西安 710055；2. 西安建筑科技大学建筑设计研究院，西安 710055；3. 结构工程与抗震教育部重点实验室，西安 710055)

在碱性及近中性土壤环境中，埋地钢管随着服役龄期的延长腐蚀逐渐加深，其力学与抗震性能不断退化．为了研究碱性及近中性土壤环境中多龄期埋地钢管的抗震性能，引入钢材时变本构模型，对埋地钢管进行了增量动力时程分析，建立了碱性及近中性土壤环境中不同服役龄期埋地钢管的概率地震需求模型．基于管线三态破坏准则，确定了各极限破坏状态的限值，进而建立了碱性和近中性土壤环境中4种不同服役龄期埋地钢管单元时变地震解析易损性模型，并绘制出相应的时变地震易损性曲线．结合震害资料的经验统计规律，对3种不同管径的多龄期埋地钢管进行了地震易损性分析．结果表明：在碱性及近中性土壤环境中，随着服役龄期的延长及管径的减小，相同地震动作用下埋地钢管在基本完好、中等破坏、严重破坏等极限破坏状态下的超越概率均逐渐增大．

碱性土壤；近中性土壤；埋地钢管；力学性能退化；多龄期；地震易损性

埋地钢管是生命线系统的重要组成构件．国内外历次强震震害资料的经验统计表明，突发地震可能造成埋地管网的功能失效，进而带来巨大的经济损失并引发社会问题[1]．近年来，我国地震发生频度及强度不断增加，然而我国多数埋地管网已服役数十年，因土壤腐蚀作用，目前处于老化及抗震性能退化严重的阶段，在突发地震作用下极易发生破坏．地震易损性作为地震灾害风险分析的重要组成部分，从概率意义上定量描述了结构的抗震性能，并从宏观上描述了地震动强度与结构破坏程度之间的关系．进行埋地钢管地震易损性分析，可以得到不同地震作用下埋地钢管出现不同破坏状态的概率，为其抗震性能评价及震后修复加固提供重要依据．

目前，关于埋地管道的地震易损性，王立功[2]及Lanzano等[3]基于历史震害资料统计，进行了地震易损性分析，他们考虑的因素不够系统全面，且存在一定局限性；刘智等[4]和Yoon等[5]考虑了管道材质、直径、埋深以及土壤参数等诸多因素，进行了理论易损性分析，但未考虑服役龄期对埋地管道地震易损性的影响．贺金川等[6]对酸性土壤环境中埋地钢管进行了时变地震易损性分析，发现随着服役龄期的延长，管道失效的累积效应增大，其对失效概率的影响随之增大．因此，开展埋地管道的时变地震易损性研究具有重要意义．

本文基于相关研究[7-9]，建立埋地钢管有限元模型，采用24条符合条件的地震动记录，对多龄期埋地钢管进行增量动力时程分析(incremental dynamic time history analysis，IDA)，进而建立碱性及近中性土壤腐蚀环境中不同服役龄期埋地钢管的地震易损性模型，并绘制出相应的地震易损性曲线，还结合震害资料的经验统计规律进一步给出不同管径多龄期埋地钢管的地震易损性曲线．

1 埋地钢管腐蚀模型

埋地钢管腐蚀的发生具有随机性，刘威等[10]采用马尔可夫过程[11]对钢管腐蚀的随机过程进行了模拟．设由未腐蚀状态转移到腐蚀状态的概率即状态转移率为，钢管腐蚀发生时刻为的概率为()，即钢管在时刻处于未腐蚀状态，但在d时间内转变为腐蚀状态，则有

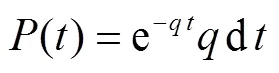
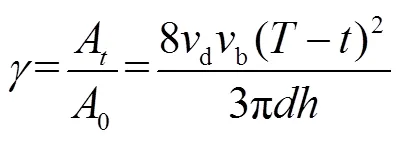
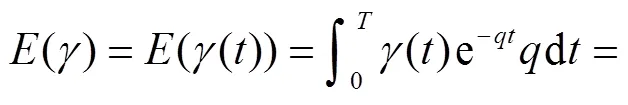
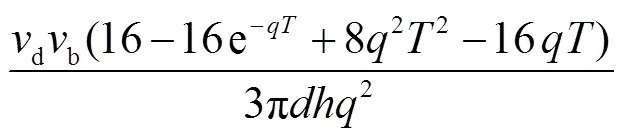
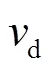
假设管道通长范围内不同截面的腐蚀率相同，钢材密度及管道长度均不因腐蚀而发生变化，则失重率w为

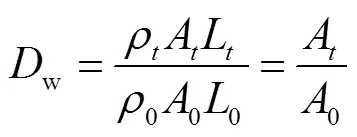
由式(2)～(4)可得碱性及近中性土壤腐蚀环境中失重率与服役龄期之间的关系为

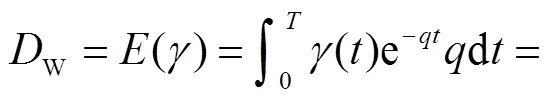
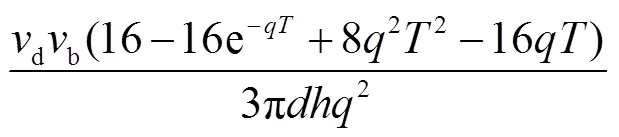
此外，文献[14]通过锈蚀钢材拉伸试验获得钢材力学性能指标随失重率增大的退化模型，即

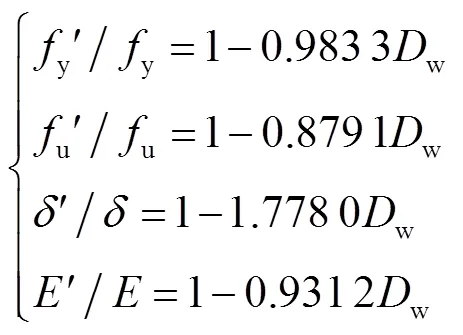
式中：y、u、和分别为钢材腐蚀前的屈服强度、极限强度、伸长率和弹性模量；y′、u′、′和′分别为钢材腐蚀后的屈服强度、极限强度、伸长率和弹性模量．结合式(5)和式(6)可得锈蚀钢材时变本构模型，进而将其应用于本文埋地钢管地震易损性 分析．

2 埋地钢管数值模型

本文基于ANSYS有限元平台，采用壳-均布弹簧模型进行埋地钢管的地震响应分析，并在管道的端部引入文献[8-9]提出的等效弹簧边界，将其以非线性弹簧的形式应用到壳单元分析模型的端部，从而考虑模型以外管段的影响，缩短单元选取长度，提高计算效率．管道-土弹簧模型如图1所示．

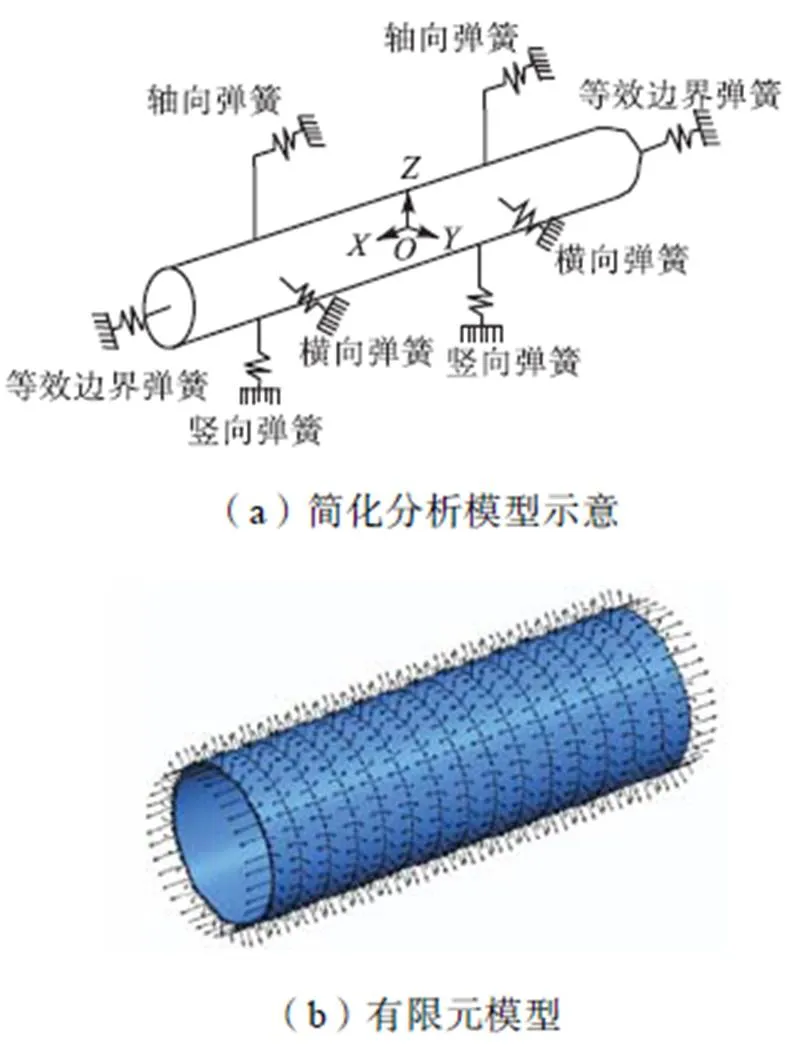
图1 管道-土弹簧模型

钢管计算长度为15m，管径为500mm，壁厚为20mm，钢材选取Q235钢，状态转移率0.2；场地类型为二类场地．本文采用4节点shell63单元模拟管道，采用combine39单元模拟弹簧，采用在各个节点上连接3个方向的弹簧单元模拟管道-土间的相互作用，并在模型两端的节点沿轴向连接一组并联弹簧，作为管道模型分析的边界．等效土弹簧及钢管等效边界弹簧的本构模型按文献[15]选取，如图2所示．钢管的本构模型采用《SY/T0450—2004输油(气)钢质管道抗震设计规范》中规定的三折线模型，如图3所示．关于在役埋地钢管有限元模型，本文仅考虑钢材力学性能的劣化，即采用锈蚀钢材时变本构模型，而模型尺寸不变．

从PEER地震动数据库中选取了ATC-63报 告[16]推荐的22条地震动记录，同时考虑到国内场地的差异性，又从中国地震台网选取了2条汶川地震动记录，如表1所示．

本文采用IDA方法进行结构的地震需求分析，为了兼顾IDA的效率与精度，选取不等步长调幅法则对所选的24条地震动记录进行调幅，统一将PGA调整为0.1、0.2、0.4、0.6、0.8、0.9、1.0.为真实反映地下管道实际遭受的地震情况，进行IDA分析时采用3向地震波输入，且将地震动水平最大分量沿着管道横向输入．

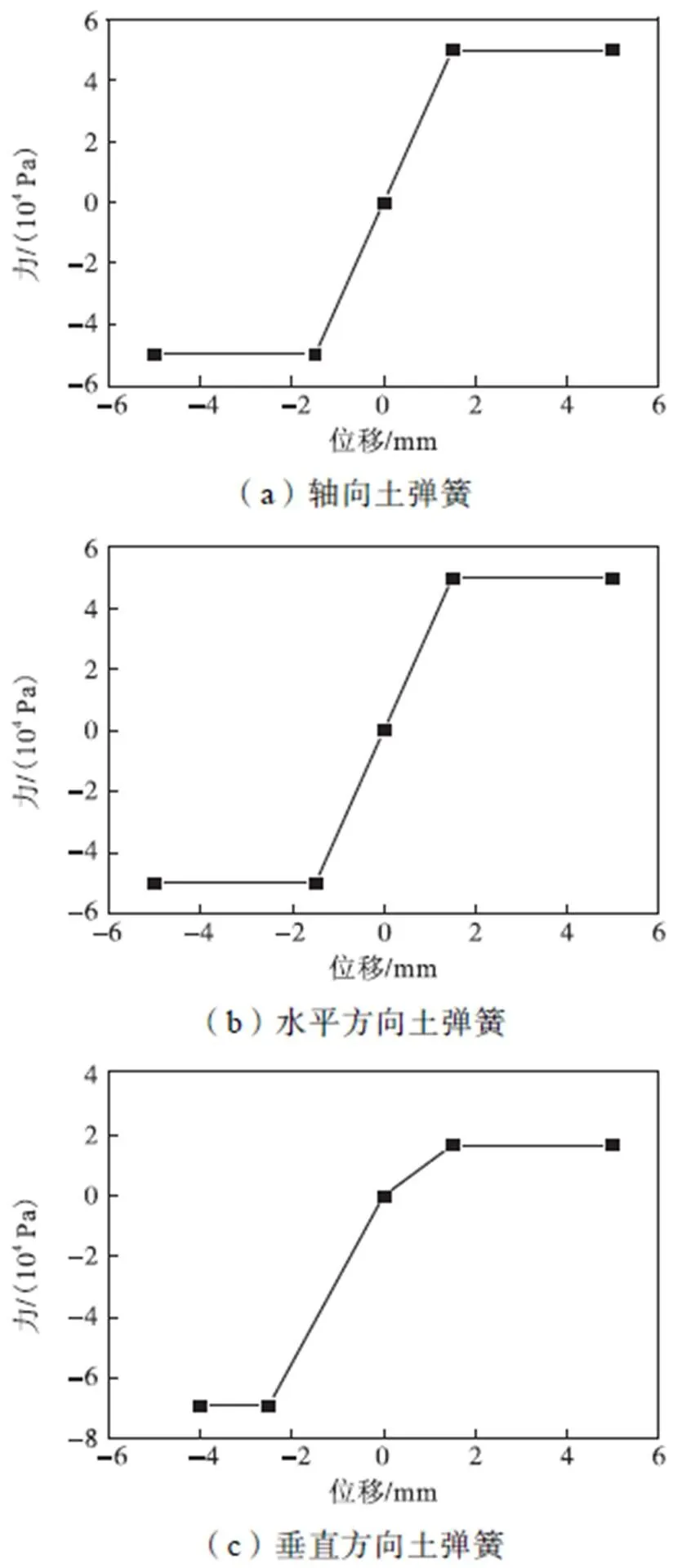
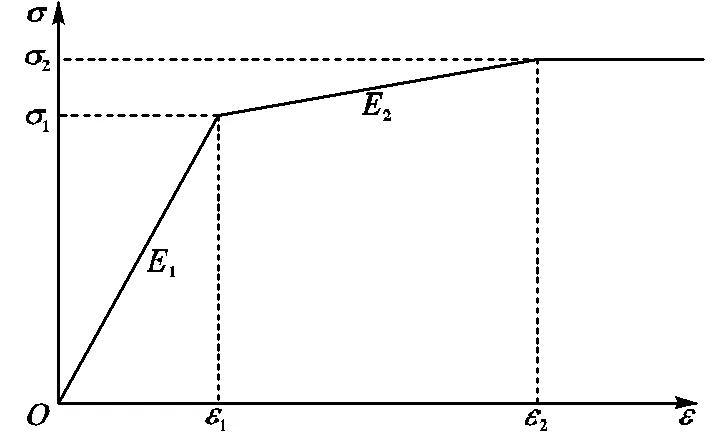
图3 钢管的三折线模型

表1 地震动记录

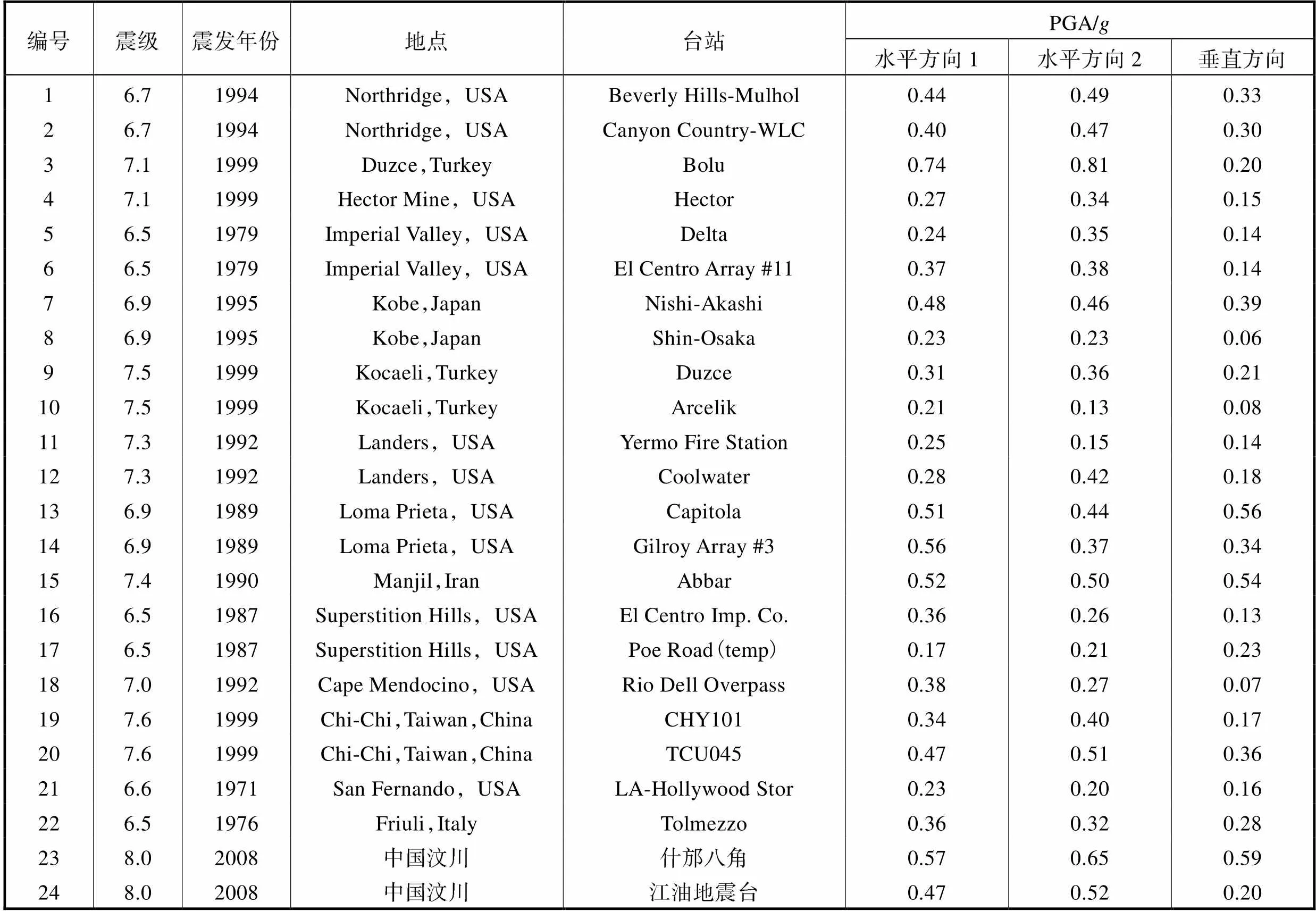
Tab.1 Acceleration records

3 地震易损性分析

3.1 概率地震需求分析

概率地震需求分析体现了不确定性从地震动到结构的传递过程，可揭示并表征地震动强度与结构响应之间的概率关系．结构地震需求的中位值|IM与地震动强度IM之间的关系为

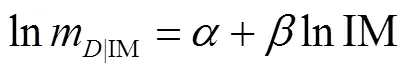
通过对结构增量动力时程分析的结果D进行对数线性拟合可得到参数和的值，并获得结构地震需求的对数标准差|IM，其计算式为

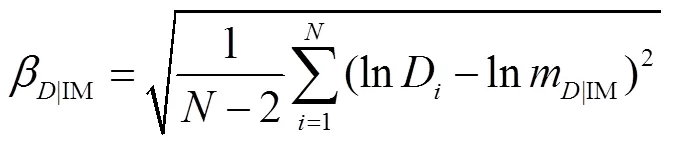
式中为回归分析中数据点的个数．

考虑不同服役龄期(10a、20a、30a、40a)的影响，分别对碱性(7.5＜pH＜8.5)及近中性(6.5＜ pH＜7.5)土壤腐蚀环境中的埋地钢管进行IDA分析，获得了以PGA作为地震动强度指标的概率地震需求模型对数线性回归结果，如图4和图5所示.

3.2 结构极限破坏状态

本文引用中国地震局工程力学研究所给出的连续焊接钢管震害破坏状况判断标准[17]：

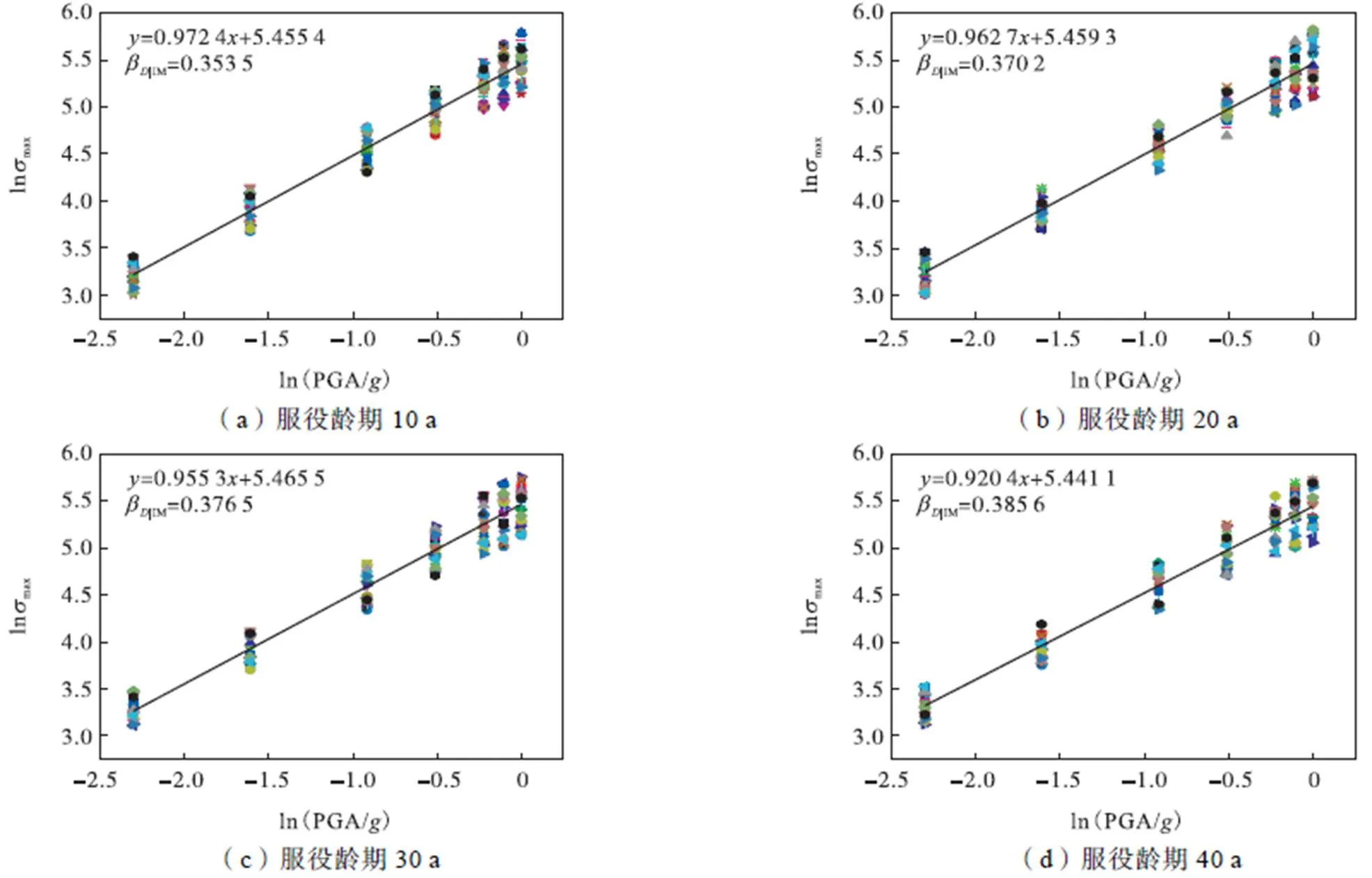
图4 碱性土壤环境中不同服役龄期埋地钢管的概率地震需求分析结果

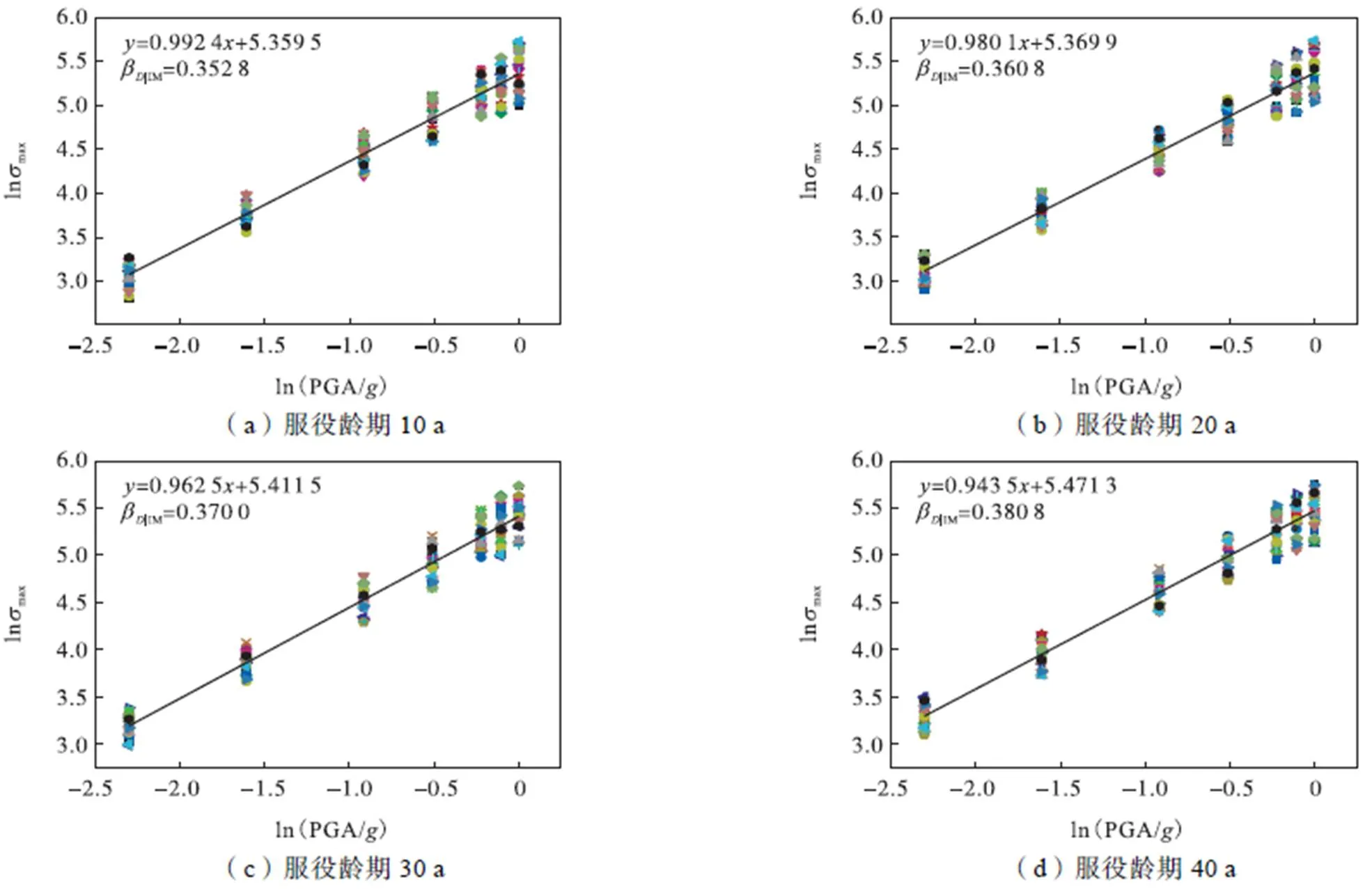
图5 近中性土壤环境中不同服役龄期埋地钢管的概率地震需求分析结果

表2 碱性土壤环境中不同服役龄期钢材的力学性能指标

Tab.2 Mechanical properties of steel of different service ages in alkaline soil

表3 碱性土壤环境中不同龄期钢管破坏状态判断标准

Tab.3 Judging standard of failure state of pipes of different service ages in alkaline soil MPa

在近中性土壤环境中，钢管腐蚀程度较轻，土壤电阻率是影响钢管腐蚀速率的主要因素．李海坤等[18]根据国内外127组钢管腐蚀速率与当地土壤电阻率的数据，建立了钢管自腐蚀速率与土壤电阻率s的关系，即

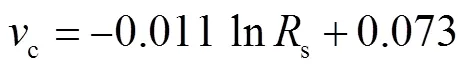
依据式(5)与式(10)可得到不同电阻率的近中性土壤环境中多龄期钢管的失重率，如表4所示．

表4 不同电阻率的近中性土壤环境中多龄期钢管的失重率

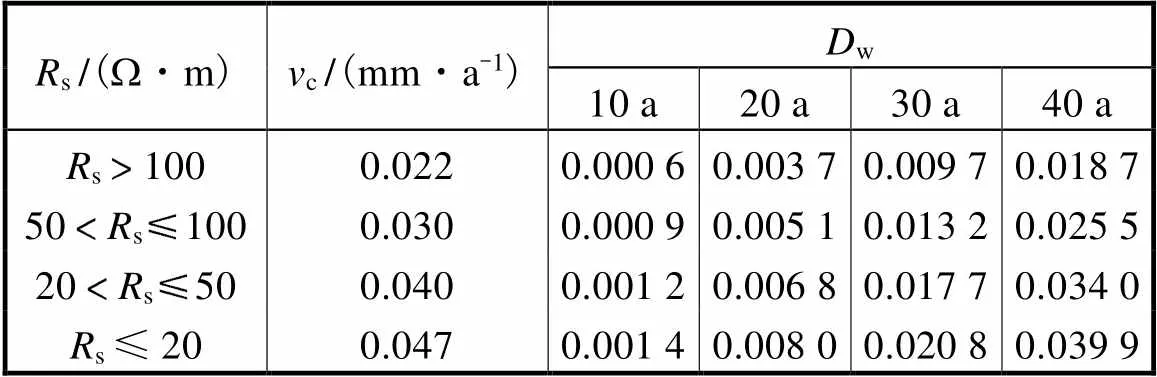
Tab.4 Weight loss rate of multiage pipes of different resistivities in near-neutral soil

由表4可以看出，近中性土壤环境下钢管的腐蚀速率随着电阻率的减小而逐渐增大，致使不同龄期的钢管失重率随着电阻率的减小而增大，且电阻率小于20W·m的土壤环境中钢管的失重率约为电阻率大于100W·m的土壤环境中失重率的2倍. 结合式(6)可得到不同电阻率近中性土壤环境中埋地钢管的弹性模量及屈服强度，如图6与图7所示.

由图6与图7可知，随着龄期的增加，钢管的弹性模量及屈服强度折减程度较小，当服役龄期为40a时，在电阻率小于20Ω·m的土壤环境中的管材弹性模量及屈服强度达到最大折减率，分别为3.72%和3.06%．不同电阻率的土壤环境中钢管的弹性模量及屈服强度随服役龄期的变化存在一定差异，但差异很小，故不考虑近中性土壤环境中的电阻率变化，采用电阻率小于20Ω·m的土壤环境中的腐蚀速率c＝0.047mm/a进行计算，得到近中性土壤环境中不同服役龄期钢材的力学性能指标及钢管破坏状态判断标准量化结果，如表5与表6所示．

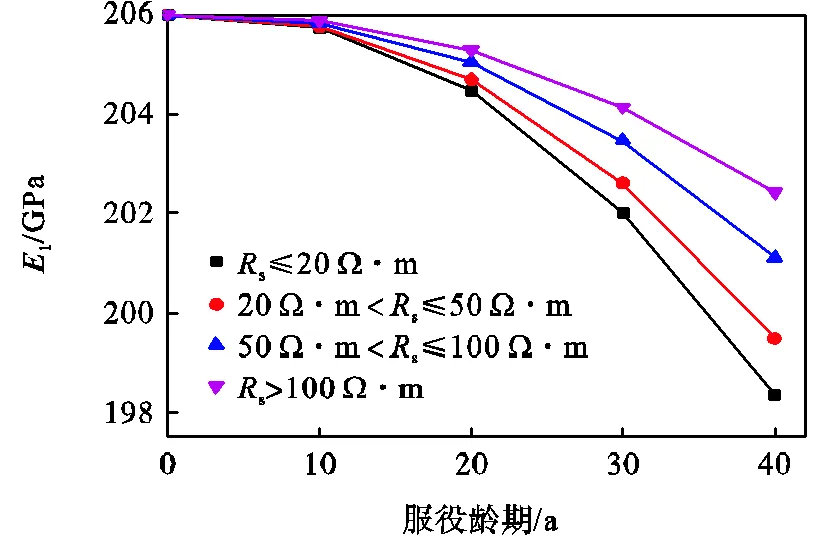
图6 弹性模量与服役龄期的关系

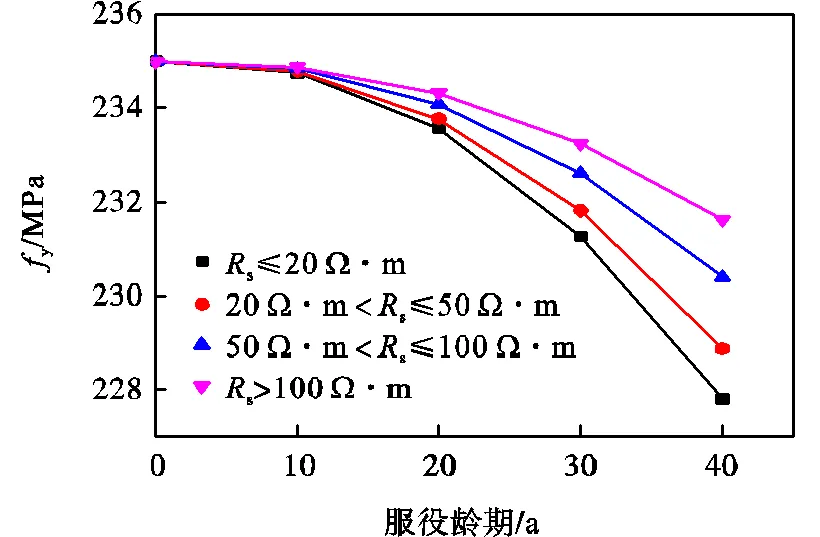
图7 屈服强度与服役龄期的关系

表5 近中性土壤环境中不同服役龄期钢材力学性能指标

Tab.5 Mechanical properties of steel of different service ages in near-neutral soil

表6 近中性土壤环境中不同服役龄期钢管破坏状态判断标准

Tab.6 Judging standard of failure state of pipes of different service ages in near-neutral soil MPa

3.3 地震易损性的解析模型

结构的地震易损性是指结构在不同强度水平地震作用下达到或超越某一极限状态的概率值．本文在结构地震易损性分析过程中，基于国内外研究，综合考虑了地震需求、抗震能力及建模的不确定性．地震需求的不确定性主要来源于地震波选取的差异、地震动特性的差异及地震强度指标选取的有效性，目前主要通过对结构的IDA分析结果进行对数线性拟合来量化地震需求的不确定性．抗震能力的不确定性主要反映结构几何特性、材料力学性能参数及结构参数等方面的不确定性，属于本质不确定性范畴，不同学者的量化方法不尽相同．建模的不确定性属于认知不确定范畴，国内外学者大都基于文献[19]进行取值．

地震易损性的解析模型为

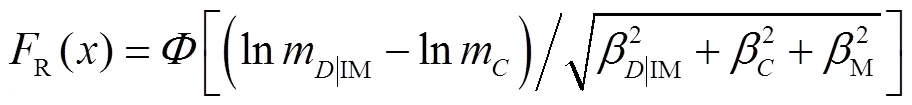
式中：R()为地震易损性函数；|IM为一定地震强度水平下结构地震需求的中位值；m为不同极限状态结构抗震能力的均值，可依据表3及表6进行取值；|IM为地震需求的不确定性，由式(8)得出；为结构抗震能力的不确定性，取＝0.25[20]；M为建模的不确定性，取为0.2[19]．

3.3.1 不同土壤腐蚀环境中不同服役龄期埋地钢管的地震易损性

将碱性及近中性土壤环境中不同服役龄期埋地钢管的概率地震需求分析结果、结构的破坏状态判断标准值以及不确定性的量化结果代入到式(11)中，得到管径为500mm位于二类场地的碱性及近中性土壤腐蚀环境中不同服役龄期埋地钢管的地震易损性模型，如表7所示，并绘制出相应的时变地震易损性曲线，如图8所示．

对比图8中碱性及近中性土壤腐蚀环境中埋地钢管单元不同服役龄期(10a、20a、30a、40a)的地震易损性曲线可以发现，相同地震强度下，不同土壤腐蚀环境中钢管单元出现不同破坏状态的概率存在显著差异，且随着服役龄期的延长，钢管单元发生破坏的概率逐渐增加．

表7 碱性及近中性土壤环境中不同服役龄期埋地钢管的地震易损性模型

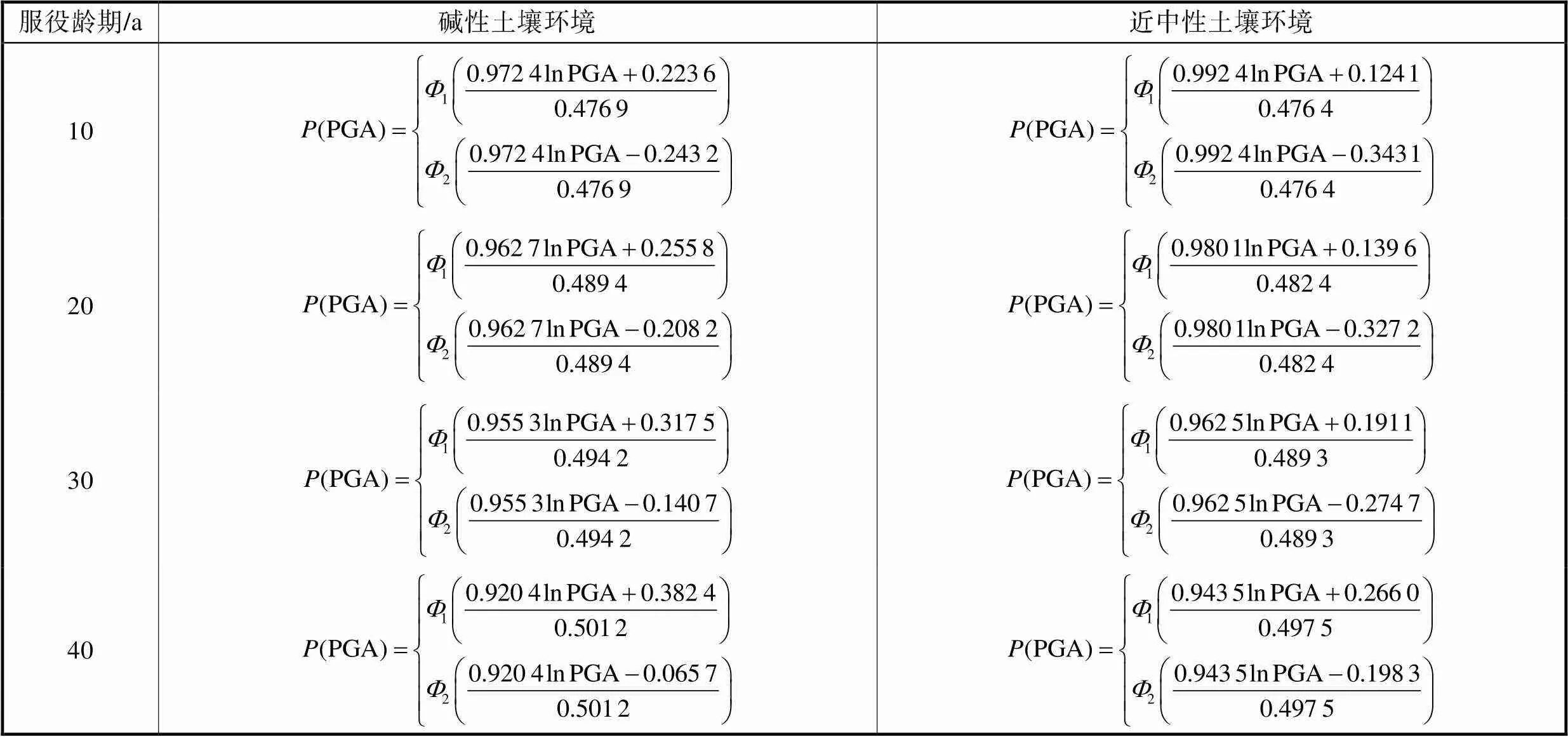
Tab.7 Seismic fragility models of buried steel pipes of different service ages in alkaline and near-neutral soils

T注：式中下标1表示基本完好极限状态；下标2表示中等破坏极限状态．

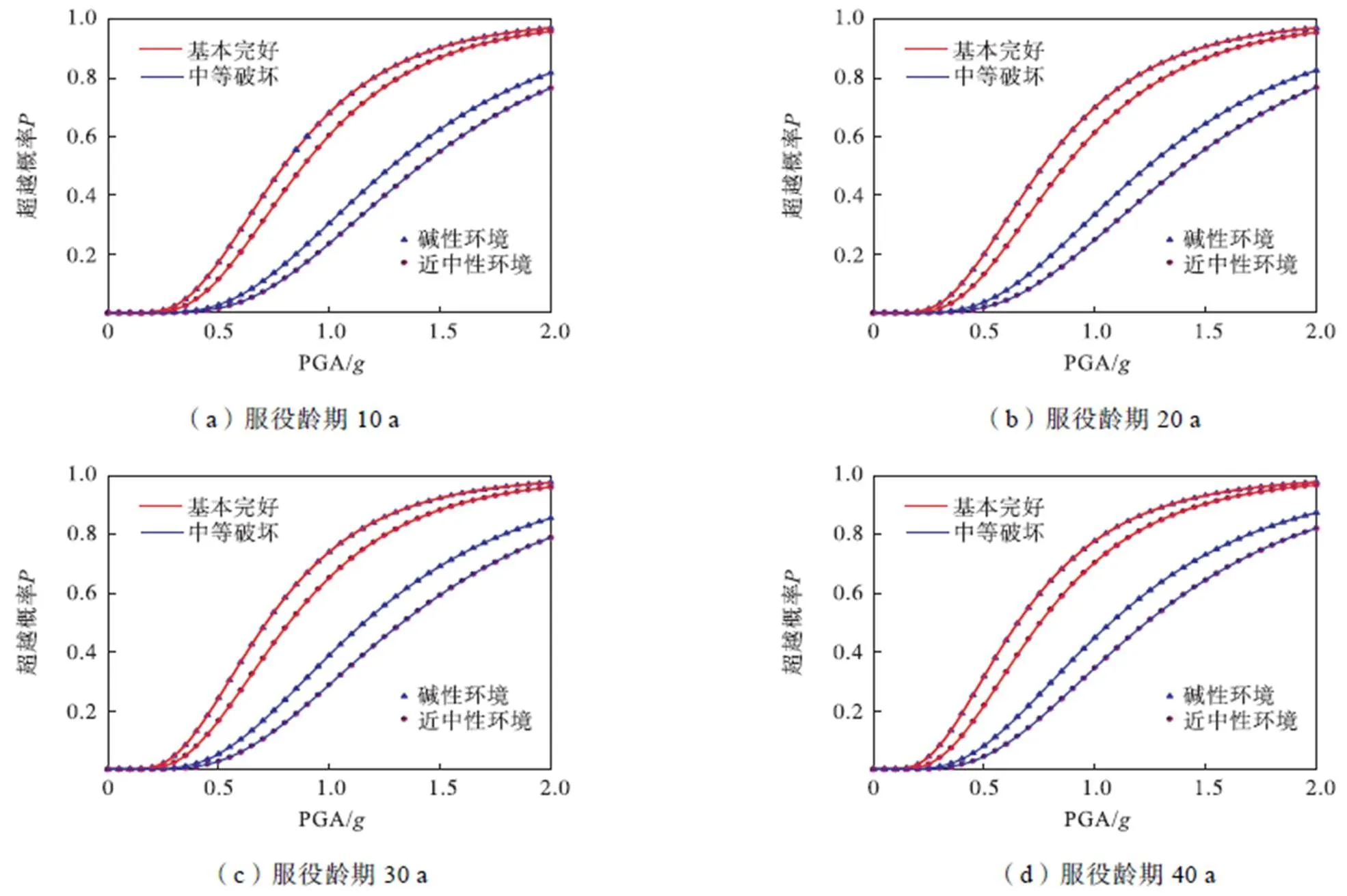
图8 碱性及近中性土壤环境中埋地钢管单元不同服役龄期的时变地震易损性曲线

3.3.2 不同管径不同服役龄期埋地钢管的地震易损性

钢管单元震后发生破坏的状态及位置一般具有偶发性，假定震害沿管段随机独立发生，且服从泊松分布，则有

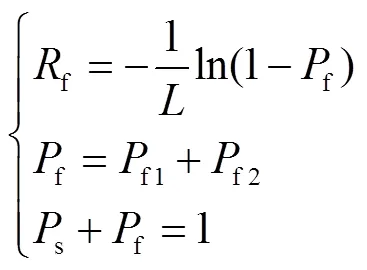
采用Shinozuka提出的考虑场地条件、管径及地震烈度3个因素的震害率表达式[21]，即

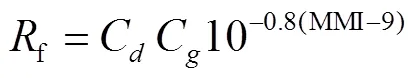
式中：MMI为修正的Mercalli烈度；C为场地影响系数；C为管径影响系数，按式(14)取值．

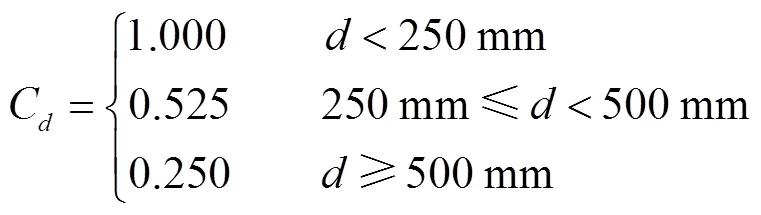
基于前文进行的管径为500mm的地震易损性分析，可得不同地震强度下埋地钢管出现不同破坏状态的破坏概率，结合式(13)与式(14)的经验统计规律，在其他参数一致的情况下进行不同管径钢管单元的时变地震易损性分析．不同管径钢管震害率的比值为

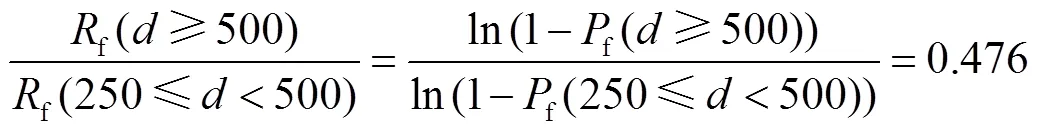
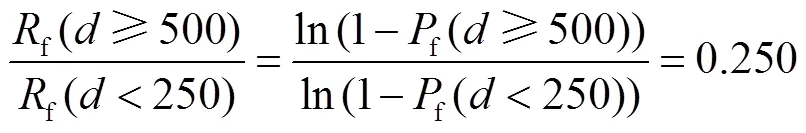
则不同管径钢管的破坏概率为

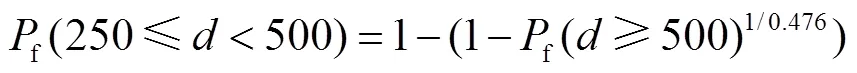
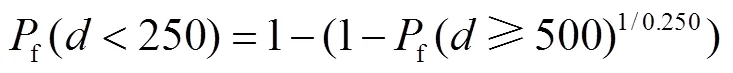
结合式(12)可得不同管径钢管出现不同破坏状态的破坏概率，基于管径为500mm的地震易损性分析结果，可得二类场地中不同管径钢管单元在不同服役龄期的时变地震易损性曲线如图9和图10所示．

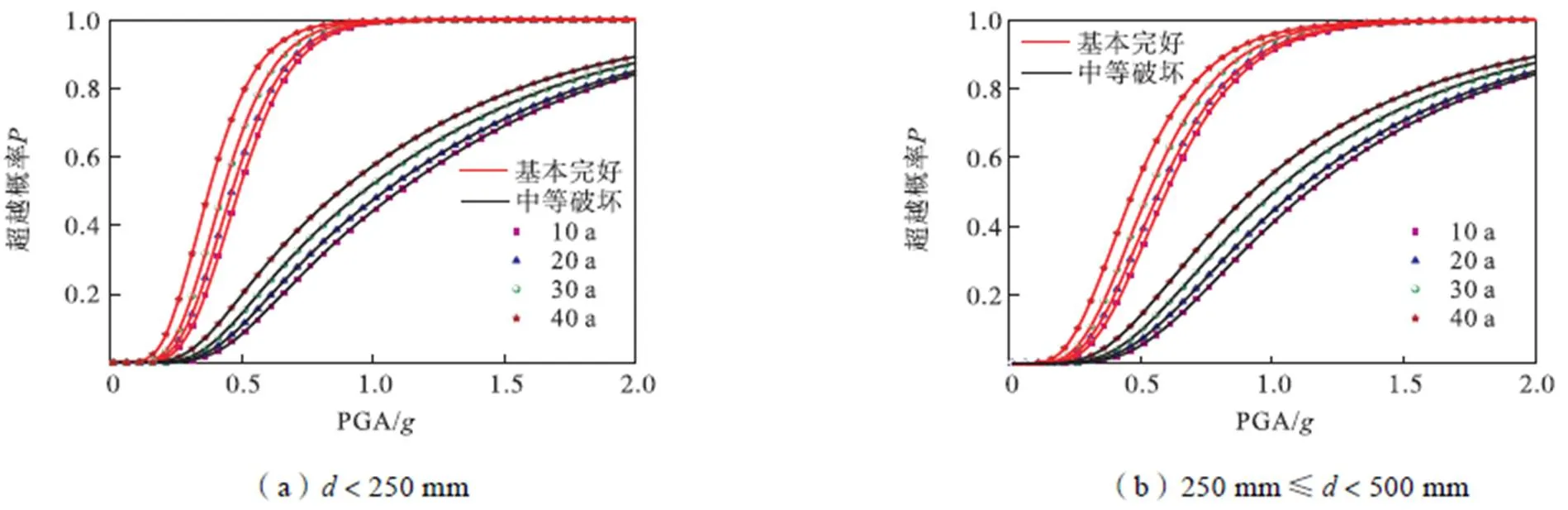
图9 碱性土壤环境中不同管径钢管单元的时变地震易损性曲线

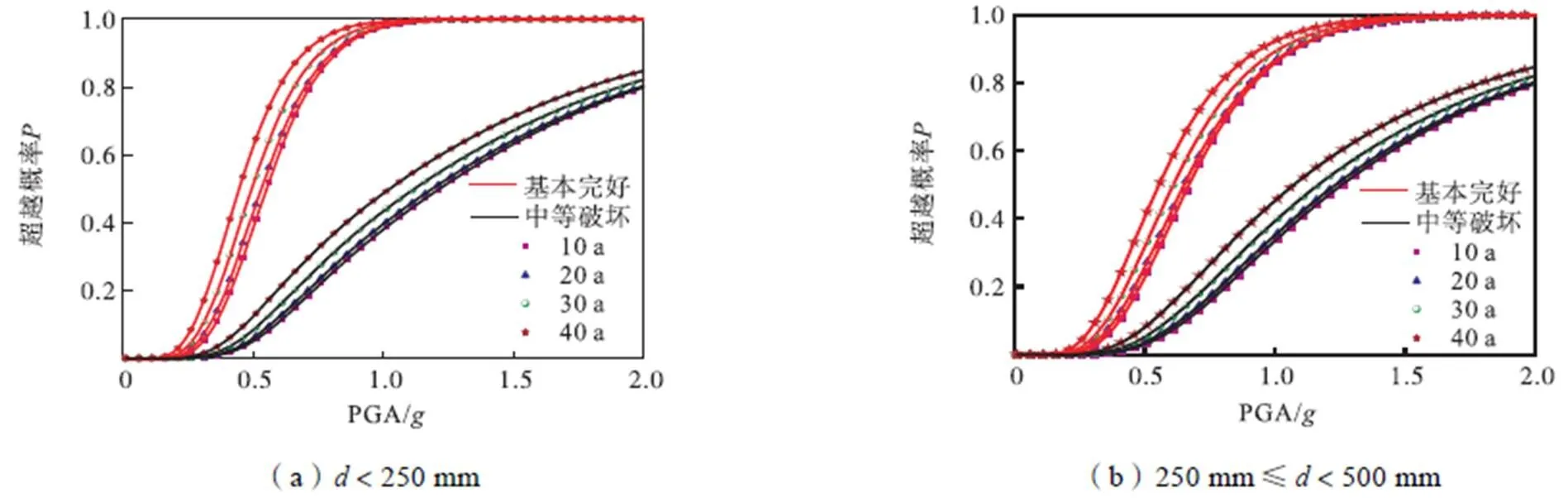
图10 近中性土壤环境中不同管径钢管单元的时变地震易损性曲线

4 结 论

(1) 基于随机腐蚀过程，建立了碱性及近中性土壤环境中埋地钢管的局部腐蚀模型；引入钢管失重率与管材力学性能退化的关系，获得了锈蚀钢材时变本构模型；基于数值模拟，对埋地钢管进行了增量动力时程分析，建立了碱性及近中性土壤环境中不同服役龄期埋地钢管的概率地震需求模型．

(2) 以等效应力为工程需求参数，基于管道三态破坏准则，确定了碱性及近中性土壤环境中不同服役龄期钢管各极限破坏状态的限值．

(3) 结合概率地震需求分析结果及钢管各破坏状态的判断标准量化结果，建立了不同土壤腐蚀环境及不同服役龄期埋地钢管的时变地震易损性模型，并绘制出相应的时变地震易损性曲线．结合震害资料的经验统计规律，进一步给出了不同管径下埋地钢管的时变地震易损性曲线．对比易损性曲线可知，在碱性及近中性土壤环境中，随着服役龄期的延长和管径的减小，相同地震动作用下埋地钢管在各极限破坏状态下的超越概率均逐渐增大．

［1］ 郭恩栋，余世舟，吴 伟. 地下管道工程震害分析[J]. 地震工程与工程振动，2006，26(3)：180-183.

Guo Endong，Yu Shizhou，Wu Wei. Seismic damage analysis of buried pipeline engineering[J]. Earthquake Engineering and Engineering Vibration，2006，26(3)：180-183(in Chinese).

［2］ 王立功. 徐州市供水生命线工程易损性分析与震害预测[J]. 华北地震科学，1985，3(1)：38-46.

Wang Ligong. Principal pipeline vulnerability analysis and prediction of earthquake hazards for water supply system in Xuzhou urban districts[J]. North China Earthquake Sciences，1985，3(1)：38-46(in Chinese).

［3］ Lanzano G，Salzano E，Santucci de Magistris F，et al. Seismic vulnerability of gas and liquid buried pipelines[J]. Journal of Loss Prevention in the Process Industries，2014，28：72-78.

［4］ 刘 智，郭恩栋，胡少卿，等. 供热管道地震易损性分析[J]. 工程力学，2013，30(7)：187-192.

Liu Zhi，Guo Endong，Hu Shaoqing，et al. Seismic vulnerability analysis of heat supply pipeline[J]. Engineering Mechanics，2013，30(7)：187-192(in Chinese).

［5］ Yoon Sungsik，Lee Do Hyung，Jung Hyung Jo. Seismic fragility analysis of a buried pipeline structure considering uncertainty of soil parameters[J]. International Journal of Pressure Vessels and Piping，2019，175：103932.

［6］ 贺金川，韩 峰，郑山锁，等. 酸性土壤环境中多龄期埋地钢管地震易损性分析[J]. 天津大学学报：自然科学与工程技术版，2020，53(9)：881-889.

He Jinchuan，Han Feng，Zheng Shansuo，et al. Seismic vulnerability analysis of multi-age buried steel pipes in an acidic soil environment[J]. Journal of Tianjin University：Science and Technology，2020，53(9)：881-889(in Chinese).

［7］ 赵 林，冯启民. 埋地管线有限元建模方法研究[J]. 地震工程与工程振动，2001，21(2)：53-57.

Zhao Lin，Feng Qimin. Research on methods of establishing FEM model of buried pipelines[J]. Earthquake Engineering and Engineering Vibration，2001，21(2)：53-57(in Chinese).

［8］ 刘爱文. 基于壳模型的埋地管道抗震分析[D]. 北京：中国地震局地球物理研究所，2002.

Liu Aiwen. Seismic Analysis of Buried Pipeline Based on Shell Model[D]. Beijing：Institute of Geophysics，China Earthquake Administration，2002(in Chinese).

［9］ 胡聿贤. 地震断层作用下埋地管线壳有限元分析的等效边界方法[J]. 地震学报，2004，26(增1)：142-148.

Hu Yuxian. Equivalent boundary method for finite element analysis of buried pipeline shell under earthquake fault[J]. Acta Seismologiga Sinica，2004，26(Suppl 1)：142-148(in Chinese).

［10］刘 威，李 杰. 考虑随机腐蚀作用的埋地管线地震反应分析[J]. 土木工程学报，2007，40(2)：104-108.

Liu Wei，Li Jie. Seismic response analysis of buried pipelines with stochastic corrosions[J]. China Civil Engineering Journal，2007，40(2)：104-108(in Chinese).

［11］刘次华. 随机过程及其应用[M]. 北京：清华大学出版社，2004.

Liu Cihua. Stochastic Process and Its Application[M]. Beijing：Tsinghua University Press，2004(in Chinese).

［12］周方勤. 在役输气管道腐蚀剩余寿命预测技术研究[D]. 成都：西南石油大学，2006.

Zhou Fangqin. Study on Prediction Technology for Residual Lifetime of Corroded Gas Pipeline in Service[D]. Chengdu：Southwest Petroleum University，2006(in Chinese).

［13］黄 涛，陈小平，王向东，等. pH值对Q235钢在模拟土壤中腐蚀行为的影响[J]. 中国腐蚀与防护学报，2016，36(1)：31-38.

Huang Tao，Chen Xiaoping，Wang Xiangdong，et al. Effect of pH value on corrosion behavior of Q235 steel in an artificial soil[J]. Journal of Chinese Society for Corrosion and Protection，2016，36(1)：31-38(in Chinese).

［14］Zheng Shansuo，Zhang Xiaohui，Zhao Xuran. Experimental investigation on seismic performance of corroded steel columns in offshore atmospheric environment[J]. Structural Design of Tall and Special Buildings，2019，28(4)：e1580.

［15］何双华，柳春光. 地下管线的抗震可靠性研究[M]. 北京：中国水利水电出版社，2014.

He Shuanghua，Liu Chunguang. Seismic Reliability Study of Underground Pipelines[M]. Beijing：China Water Conservancy and Hydropower Press，2014(in Chinese).

［16］Applied Technology Council，Federal Emergency Management Agency. Quantification of Building Seismic Performance FActors[R]. America：FEMA，2008.

［17］郭恩栋，刘如山，孙柏涛. 地下管线工程地震破坏等级划分标准[J]. 自然灾害学报，2007，16(4)：86-90.

Guo Endong，Liu Rushan，Sun Baitao. Gradation criterion of earthquake damage to buried pipeline engineering[J]. Journal of Natural Disasters，2007，16(4)：86-90(in Chinese).

［18］李海坤，朱凤艳，娄月霞，等. 不同电阻率土壤中管道钢的自腐蚀速率分布[J]. 腐蚀与防护，2017，38(8)：598-601.

Li Haikun，Zhu Fengyan，Lou Yuexia，et al. Distribution of free corrosion rate of pipeline steel in soil with different resistivity[J]. Corrosion and Protec-tion，2017，38(8)：598-601(in Chinese).

［19］Kinali K，Ellingwood B R. Seismic fragility assessment of steel frames for consequence-based engineering：A case study for Memphis，TN[J]. Engineering Structures，2007，29(6)：1115-1127.

［20］Ellingwood B R，Kinali K. Quantifying and communicating uncertainty in seismic risk assessment[J]. Structural Safety，2009，31(2)：179-187.

［21］Hwang H H M，Lin H，Shinozuka M. Seismic performance assessment of water delivery systems[J]. Journal of Infrastructure Systems，1998，4(3)：118-125.

Time-Varying Seismic Fragility Analysis of Buried Steel Pipes in Alkaline and Near-Neutral Soil Environments

Xie Xiaokui1，He Jinchuan2，Zheng Shansuo1, 3，Han Feng1, 3，Cai Yonglong3

(1. School of Civil Engineering，Xi’an University of Architecture and Technology，Xi’an 710055，China；2. Architectural Design and Research Institute，Xi’an University of Architecture and Technology，Xi’an 710055，China；3. Key Laboratory of Structural Engineering and Earthquake Resistance of Ministry of Education of China，Xi’an 710055，China)

In alkaline and near-neutral soil environments，the mechanical and seismic performance of buried steel pipes degrades with deepening corrosion over time．To study the seismic fragility of buried steel pipes of different service ages in these environments，an incremental dynamic time history analysis of typical pipes was carried out with the time-varying constitutive model of steel．A probabilistic seismic demand model for buried steel pipes of different service ages in alkaline and near-neutral soil environments was then established ，which can characterize the probability relationship between the ground motion intensity and structural response．Furthermore，on the basis of the tristate criteria，the limits of each ultimate failure state were determined．Time-varying seismic analytical fragility models of the pipes，including pipe units in two different soil environments and four service ages，were then established ，which can characterize the probability of different failure states of structures under different earthquakes．The corresponding seismic fragility curves were then drawn．Seismic fragility curves were also obtained within three different diameter ranges based on seismic damage statistics．Results showed that，under the same ground motion，with increasing service time and decreasing pipe diameter，the probabilities of three failure states，namely，basically intact，moderately damaged，and severely damaged，all increased．

alkaline soil；near-neutral soil；buried steel pipe；degeneration of mechanical property；multiage；seismic fragility

P315.9

A

0493-2137(2020)12-1254-10

10.11784/tdxbz201908007

2019-08-04；

2019-09-16.

谢孝奎（1995—  ），男，博士研究生，xiexiaokui1995@163.com.

贺金川，1138088650@qq.com

国家重点研发计划资助项目(2019YFC1509302)；国家自然科学基金资助项目(51678475)；西安市科技计划资助项目 (2019113813CXSF016SF026)；陕西省教育厅产业化项目(18JC020).

Supported by National Key Research and Development Project(No. 2019YFC1509302)，the National Natural Science Foundation of China (No. 51678475)，Xi'an Science and Technology Program(No. 2019113813CXSF016SF026)，the Industrialization Program of Education Department of Shaanxi Provincial Government(No. 18JC020).

(责任编辑：刘文革，樊素英)