Sweedler’s dual of Hopf algebras in

Zhang Tao Wang Shuanhong

(School of Mathematics, Southeast University, Nanjing 211189, China)

Abstract：Firstly, the notion of the left-left Yetter-Drinfeld quasicomodule M=(M,·,ρ) over a Hopf coquasigroup H is given, which generalizes the left-left Yetter-Drinfeld module over Hopf algebras. Secondly, the braided monoidal category is introduced and the specific structure maps are given. Thirdly, Sweedler’s dual of infinite-dimensional Hopf algebras in is discussed. It proves that if (B,mB,μB, ΔB, εB) is a Hopf algebra in with antipode SB, then (B0,(mB0)op, (ΔB0)op, which generalizes the corresponding results over Hopf algebras.

Key words：Hopf (co)quasigroup; Yetter-Drinfeld quasi(co)module; braided monoidal category; duality

LetHbe a Hopf algebra. Schauenburg[1]obtained a braided monoidal category equivalence between the category of right-right Yetter-Drinfeld modules overHand the category of two-sided two-cosided Hopf modules overHunder some suitable assumption. This yields new sources of braiding by which one can obtain the solutions to the Yang-Baxter equation, which plays a fundamental role in various areas of mathematics[23].

The most well-known examples of Hopf algebras are the linear spans of (arbitrary) groups. Dually, also the vector space of linear functionals on a finite group carries the structure of a Hopf algebra. In the case of quasigroups (nonassociative groups), however, it is no longer a Hopf algebra, but more generally, a Hopf quasigroup[510], which is a specific case of the notion of unital coassociative bialgebra[11].

Throughout this paper, letkbe a fixed field. We will work overk. LetCbe a coalgebra with a coproductΔ. We will use Heyneman-Sweedler’s notation[12],Δ(c)=∑c1⊗c2for allc∈C, for coproduct.

1 Preliminaries

Recall from Ref.[5] that a Hopf coquasigroup is a unital associative algebraH，armed with three linear maps:Δ:H→H⊗H，ε:H→KandS:H→Hsatisfying the following equations for alla,b∈H:

Δ(ab)=Δ(a)Δ(b)

ε(ab)=ε(a)ε(b)

(id⊗ε)Δ(a)=a=(ε⊗id)Δ(a)

∑S(a1)a21⊗a22=1⊗a=∑a1S(a21)⊗a22

∑a11⊗S(a12)a2=a⊗1=∑a11⊗a12S(a2)

Recall from Ref.[6], the authors gave the notion of a leftH-quasimodule over a Hopf quasigroupH. Duality, a leftH-quasicomodule over a Hopf coquasigroupHis a vector spaceMwith a linear mapρ:M→H⊗M, whereρ(m)=∑m-1⊗m0such that ∑ε(m-1)m0=mand

∑S(m-1)m0-1⊗m00=∑m-1S(m0-1)⊗m00=1⊗m

for allm∈M.

Moreover, the authors studied the notion of the left-left Yetter-Drinfeld quasimoduleM=(M,·,ρ) over a Hopf quasigroupH.

Duality, a left-left Yetter-Drinfeld quasicomoduleM=(M,·,ρ) over a Hopf coquasigroupHis a leftH-module (M,·) and a leftH-quasicomodule (M,·) satisfying the following equations:

∑(a1·m)-1a2⊗(a1·m)0=∑a1m-1⊗a2·m0

∑a1·m⊗a21⊗a22=∑a11·m⊗a12⊗a2

∑a1⊗a21·m⊗a22=∑a11⊗a12·m⊗a2

for alla∈H,m∈M.

Remark that the first equation is equivalent to the following formula:

ρ(a·m)=∑a11m-1S(a2)⊗a12·m0

τ:M⊗N→N⊗M,τ(m⊗n)=∑m-1·n⊗m0

τ-1:N⊗M→M⊗N,τ-1(n⊗m)=∑m0⊗S-1(m-1)·n

One can check the following lemmas and Corollary 1.

∑m-11·n⊗m-12·p⊗m0=∑m-1·n⊗m0-1·p⊗m00

Corollary1LetHbe a Hopf coquasigroup with a bijective antipodeS. If the following equations hold:

∑m-11·n⊗m-12⊗m0=∑m-1·n⊗m0-1⊗m00

∑m-11⊗m-12·n⊗m0=∑m-1⊗m0-1·n⊗m00

LetHbe a Hopf coquasigroup with a bijective antipodeS. Under the hypotheses of the above results, we have the relationship:

Δ(xy)=∑x1(x2-1·y1)⊗x20y2,Δ(1)=1⊗1

ε(xy)=ε(x)ε(y),ε(1H)=1

ρH(xy)=∑(xy)-1⊗(xy)0=

∑x-1y-1⊗x0y0,ρH(1H)=1L⊗1H

∑x-1⊗x01⊗x02=∑x1-1x2-1⊗x10⊗x20

∑x-1εH(x0)=εH(x)1

l·(xy)=∑(l1·x)(l2·y),l·1H=ε(l)1H

Δ(l·x)=∑(l1·x1)⊗(l2·x2),ε(l·x)=ε(l)ε(x)

SH(xy)=∑((S(x))-1·SH(y))(S(x))0=

∑(x-1·S(y))S(x0),S(1)=1

SH(xy)=∑((S(x))-1·SH(y))(S(x))0=

∑(x-1·S(y))S(x0),S(1)=1

for anyx,y∈Handl∈L.

2 A Generalization of Sweedler’s Dual of Hopf Algebras

Let (A,mA,μA) be an associative algebra. Then, we have coalgebraA0given in Ref.[13] as

A0={f∈A*|Kerf⊃an ideal ofAof cofinite dimension}

dim(fB)<∞,dim(B⇀fB)<∞

For anyf∈B*anda,b∈B, we define (a⇀f)(b)=f(ba) and (fa)(b)=f(ab). This defines aB-Bbimodule structure onB*.

We consider the action ofHonB*given by (h·f)(b)=f(S(h) ·b) and the quasicoaction ofHonB*defined byρ(f)(b)=S-1(b(-1))⊗f(b0) for allh∈H,b∈Bandf∈B*.

It is not difficult for one to check the following two lemmas.

Lemma3The action:B*⊗B→Bis a leftH-linear and the action ⇀:B⊗B*→Bis a leftHcop-linear.

ProofBy Lemma 3, for anyf,g∈B*anda,b∈B, we obtain

((fg)a)(b)=(fg)(ab)=(f⊗g)Δ(ab)=

f(a1(a2(-1)·b1)g(a20b2)=

f(a2(-1)2·[(S-1(a2(-1)1)·a1)b1])g(a20b2)=

(S-1(a2(-1)2)·f)[(S-1(a2(-1)1)·a1)b1]×

g(a20b2)=[(S-1(a2(-1)2)·f)

(S-1(a2(-1)1)·a1)](b1)(ga20)(b2)=

Δ*[(S-1(a2(-1))·(fa1)⊗ga20)](b)

Thus,

(fg)B⊆Δ*[H·(fB)⊗gB]⊆Δ*[(H·f)B)⊗gB]

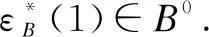
ProofApplying the quasicoaction ofHonB*, the proof is complete.

ProofAccording to Ref.[13], we check that

1)B0is anH-subquasicomodule ofB*.

4) (ΔB0)op:(B0)op→(B0)op⊗(B0)opis an algebra map.

In the setting of Hopf coquasigroups, the notion of the leftH-module is exactly the same as that for ordinary Hopf algebras since it only depends on the algebra structure ofH. Thus, the proof of these assertions is either trivial or will become trivial after acquainting the Hopf coquasigroup calculus developed above.