基于多源储能节点拓扑特征的交直流新能源电网功率平衡分区控制

冷欧阳， 回 茜， 左 浩， 刘 鑫

（1. 国网内蒙古东部电力有限公司 经济技术研究院， 内蒙古 呼和浩特 010020； 2.国网辽宁营销服务中心，辽宁 沈阳 110004； 3.沈阳工业大学， 辽宁 沈阳 110870）

0 引言

随着世界各国能源互联网战略的提出和稳步实施，电力系统中多种能源形式的负荷及储能设备、单机大容量分布式的可再生能源发电设备等接入规模和占比也在快速增长[1]～[3]。 一方面，多种能源形式和可再生能源接入规模的增长在有效推进能源产业升级与可持续能源利用水平提升的同时，还可为电力系统提供更多更有效的动态和暂态功率控制手段；另一方面，多种能源形式间及负荷与储能间的复杂拓扑与能量转换关系，可再生能源波动的随机性，都将给交直流混联电力系统功率平衡能力与紧急功率控制带来新的挑战[4]～[6]。 因此，在交直流混联的新能源电网动态优化控制过程中，如何根据不同的多能源储能支撑能力及可再生能源波动特性对系统进行分布式协调控制受到了国内外学者的广泛关注，也是目前能源互联网领域研究的热点和难点之一。

针对交直流混合系统的稳定控制问题，国内外学者进行了大量研究。 文献[7]提出了交直流同质化能量函数模型，可实现变换器在交流、直流子系统中按照自身容量特性承担相应功率。 文献[8]，[9]提出了交直流互联变换器的自适应控制策略，使功率在子系统间合理地双向流动，实现了交直流混合系统的协调运行。 文献[10]，[11]计及大规模可再生能源不确定性， 提出了交直流混联系统的鲁棒控制方法。

储能系统具有削峰填谷特性， 可为电网提供较高的灵活调节能力。文献[12]针对超大规模储能系统在电网中的分布式接入特性， 研究电网全域范围储能系统协调优化模型， 建立了基于分布式交替方向乘子法的储能系统集群优化算法。 文献[13] 针对分布式储能系统参与电网调节能力提升问题， 研究了不同储能电价激励下分布式储能参与需求侧响应、 电网调峰和新能源远距离输送辅助服务成本优化方法， 建立了基于多模式经济性指标的分布式储能协调优化模型。文献[14]针对分布式储能在不同应用场景下的运行经济性评价问题， 对基于大数据和互联网模式下的分布式储能参与电网优化运行的经济性指标及运行策略进行了研究和分析。

本文在现有国内外研究成果基础上，针对新能源高占比的交直流混联送端电网在本地负荷和外送负荷波动下的电网功率平衡控制问题，研究基于分布式多能源储能节点与交直流混合节点的拓扑相关度模型；在此基础上研究基于各类节点同质化尺度与节点间能量交互约束的动态电网节点分区的马尔科夫能量场模型，进而研究基于马尔科夫先验知识模型的交直流新能源电网功率扰动动态分区优化控制算法；最后在东北某送端电网运行数据及IEEE39 节点模型基础上， 建立基于节点拓扑关联度动态分区的电网功率扰动分区控制仿真模型。 仿真结果及分析表明，本文提出的电网功率不平衡扰动动态分区控制模型能够有效减小火电机组和直流系统功率波动，提升送端电网功率平衡能力。

1 交直流电网节点关联度模型

在对交直流混联新能源电网进行分区时，设由节点集合表示的电网为

式中：xs，xr∈X 是电网X 的任意两个相邻节点；S为电网的节点总数。

与xs，xr都存在能量交互的相邻节点xu的能量交互越多，则两节点的关联度越大；反之，如果与两个相邻节点xs，xr都存在能量交互的相邻节点xu的能量交互越少，则两节点的关联度越小。

本文参考文献[15]的拓扑关联度模型，定义交直流混联新能源电网两个相邻节点xs，xr的拓扑能量关联度tsr为

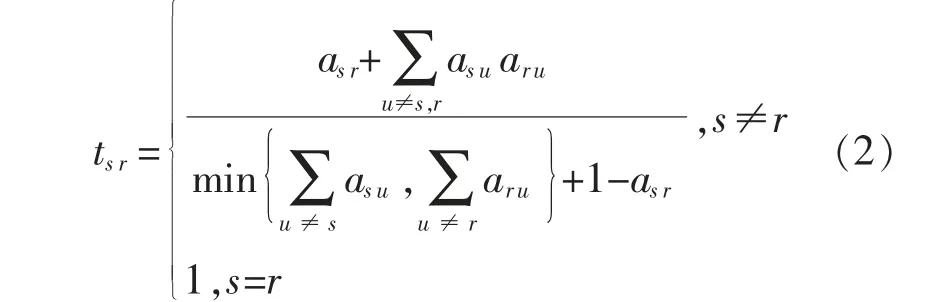
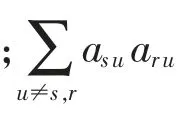
由于交直流的能量可同质化[7]，因此采用该模型可较好地表达出含大规模储能的交直流系统不同节点的关联程度。

由式（2）可知，电网X 中与两个相邻节点xs，xr都存在能量交互的节点xu的数量和能量交互量越大，那么交直流混联新能源电网X 的拓扑能量关联度tsr越大，反之则越小，且满足0≤tsr≤1。则可得交直流混联新能源电力系统的节点拓扑能量关联矩阵为

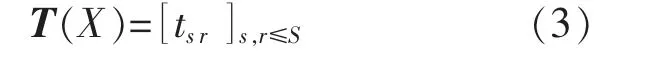
在电力系统中只有具有支路连接的两节点间才可能存在能量交互，因此式（3）的交直流混联电力系统节点拓扑关联矩阵T（X）是一个对称且非负矩阵。同时，交直流混联电力系统节点拓扑关联矩阵T（X）还能够将电网中相邻节点的可同质化特性及储能共享度等特征映射到多变量高阶节点关联矩阵中， 并利用高阶关联矩阵对电网节点的高阶同质化与储能约束进行描述， 从而实现对交直流混联电力系统引入多能源节点高阶拓扑空间相关性的表达， 最终实现对多能源节点接入后电网的局部空间特征的描述， 同时减少由于多能源储能与交直流能量流数据异构等带来的交直流混联电力系统节点间相关性量化困难的问题。

2 交直流电网节点分区模型

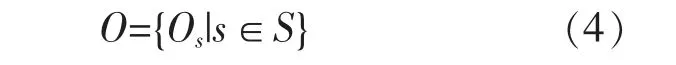
设用等值电网节点表示的交直流混联电力系统中某局部区域为式中：S={s|s≤M×N} 表示交直流混联电力系统中的一个有限节点集， 且该节点集的容量为M×N；Os表示节点s 的有能量交互的相邻节点集。

若已知一个交直流新能源电力系统：

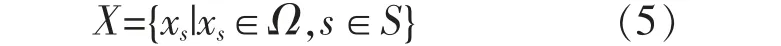
式中：Ω= -1，［ ］

1 为电力系统中节点xs的储能需求， 表示有多源储能装置接入的节点对储能装置运行方式的需求可能是从100%额定功率充能到100%额定功率放能之间变化。

设节点xs的注入能量为ys， 并将交直流新能源电网划分为Λ={0，1，…，L}个区域，则可得到各区域内电网的能量场

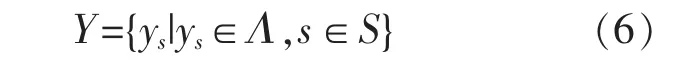
考虑式（6）的交直流新能源电网的分区能量场Y 为一个马尔科夫随机场，则在给定的电网运行方式X 下得到分区能量场Y 概率为

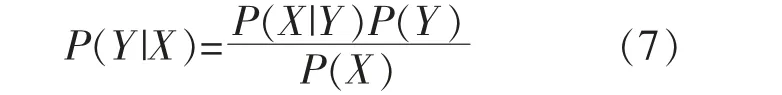
在电网运行状态X 的切换过程中，电网分区能量场Y 的动态求解过程即转化为求取其全局最优估计解Y*。 这个全局最优分区能量场Y*的估计问题又可转化成节点能量不平衡的最小化问题：

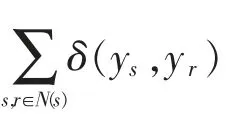
3 节点动态分区先验模型

在交直流新能源电网的动态分区中， 电网局部区域中蕴含的全局能量平衡信息是进行基于能量平衡优化的分区动态调整的重要关键先验知识。全局能量信息是基于电网节点间，尤其是电网多源储能节点间的关联度描述的。同时，简单节点间能量交互关联度难以全面反映交直流新能源电网局部的能量场空间特征。

令yr∈Os（ys）表示节点ys的区域节点集合的一个子集节点，Os（ys）表示节点ys的区域ws内相邻且有直接能量交互的节点集合， 则任意两个相邻节点xs，xr的能量关联度tsr（xs，xr）为

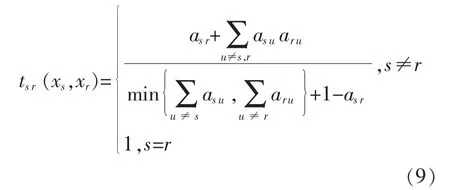
式中：s≠r 时，asr表示节点xs，xr间的能量交互强度。

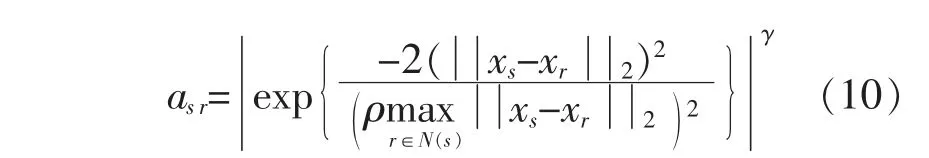
由式（9），（10）可知，如果相邻节点xs，xr分别与其共享节点具有能量交互， 那么相邻节点xs，xr的拓扑重叠测度tsr（xs，xr）的值更大，也就是说，对于两个相邻节点xs，xr，如果节点xs和其多个共享节点具有较高能量关联度，节点xr也与这几个共享节点具有较高能量关联度。 根据节点能量传递性质可知，这两个相邻节点xs，xr也具有较高能量关联度，即能量关联度tsr（xs，xr）具有更大的值，反之亦然。

若节点xr是一个新能源节点，那么无储能节点xr与其共享节点具有较低能量关联度，而有储能节点xs与其共享节点相似性较高，则相邻节点xs，xr的能量关联度tsr（xs，xr）具有较小的值。

由式（9），（10）分析可知，基于多节点能量关联度的节点间作用关系度量方法引入了交直流新能源电网局部区域节点的拓扑空间关系， 因而该模型对新能源发电波动、交直流混合节点、多源储能节点的协调具有鲁棒性。

在交直流新能源电网局部区域ws内节点关联度的高阶拓扑空间先验tws（xs，xos）为

式中：tN1（·），tN2（·），…，tNi（·） 分别为交直流新能源电网局部区域拓扑结构中节点xs与其所有相邻且具有能量交互的节点的拓扑能量关联度，即交直流新能源电网局部区域ws的高阶拓扑空间能量交互关联度先验tws（xs，xOs）值为该区域中节点xs与其相邻节点能量关联度tNi（·）之和。

在某一现有交直流新能源电网分区内， 电网节点拓扑关联度的高阶先验能量为

式中：Eh（xw|B）为交直流新能源电网分区ws内的高阶拓扑结构先验能量；B=（ρ，γ） 为交直流新能源电网分区高阶先验模型参数，ρ 为交直流及多能源同质化尺度参数，γ 为相邻且有直接能量交互节点间的能量越限惩罚因子。

由式（12）可知，基于交直流新能源电网分区节点拓扑关联度的高阶先验模型， 在对电网进行动态分区时，首先在现有的分区拓扑结构基础上，利用现有分区节点的能量关联度描述交直流新能源电网现有分区区域内具有多能源储能节点共享的相邻节点间的能量关联度， 并可在其基础上构建分区内各节点的高阶空间拓扑关系模型； 进而利用交直流新能源电网分区空间拓扑关系对节点的高阶拓扑能量关联度进行计算， 建立具有交直流新能源电网分区节点拓扑高阶空间相关性的多能源储能节点关联度先验知识表达模型， 对交直流新能源电网现有分区区域内蕴含的节点间复杂拓扑空间结构特征等高阶先验知识进行描述。

4 交直流新能源电网分区算法

在前文的交直流新能源电网分区动态先验知识模型中考虑了交直流同质化节点、多能源同质化节点及储能节点在分区调整时的变化，所以分区的拓扑先验知识能够提供交直流新能源电网对新能源波动、负荷波动、多能源协调等方面的控制能力指标。 因此，该模型可以降低新能源波动造成的节点间功率交互突变所带来的节点间能量相关度畸变、 对电源和负荷扰动等影响，具有较强的鲁棒性。

基于先验知识模型的交直流新能源电网动态分区模型具体算法如图1 所示。

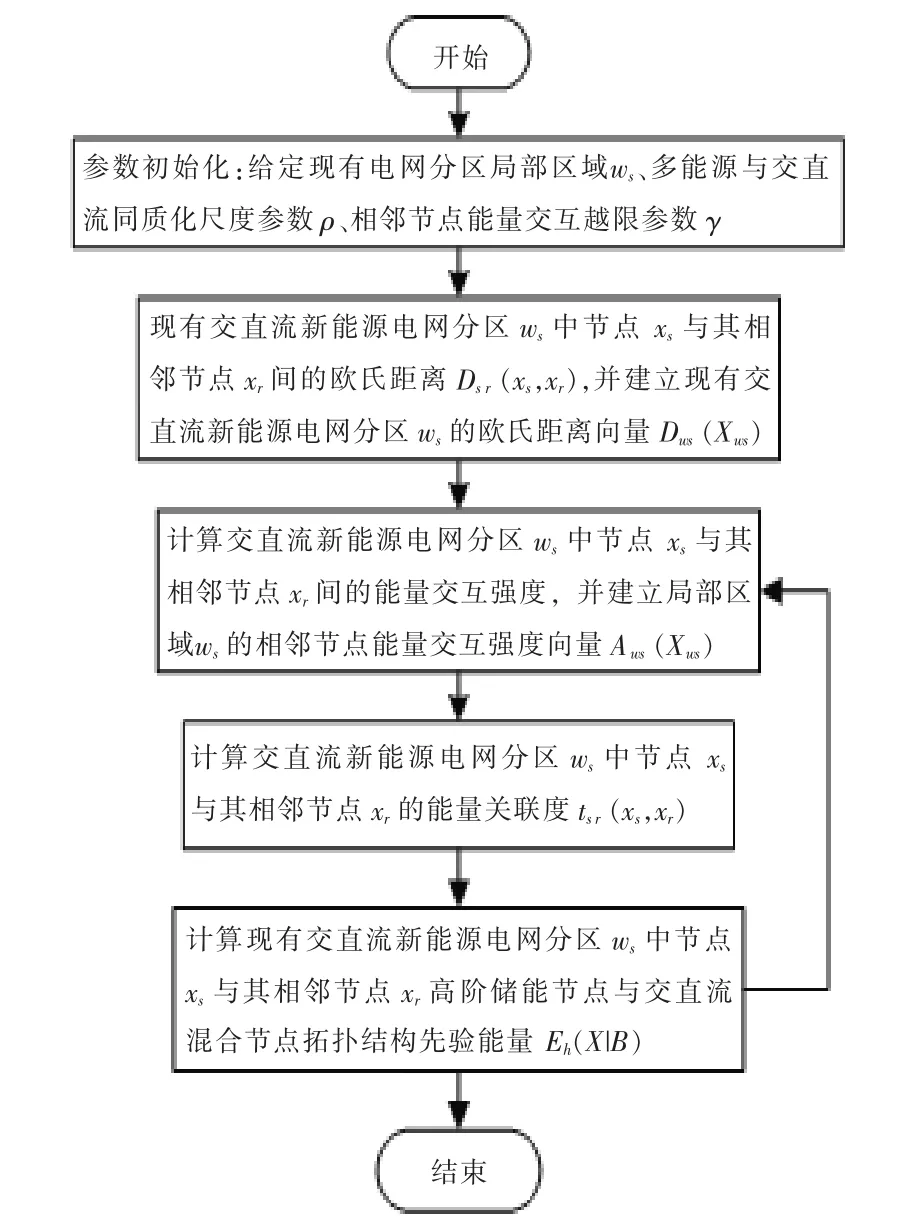
图1 算法流程图Fig.1 Algorithm flow char

基于先验知识模型的交直流新能源电网动态分区模型如下。

模型输入： 包含多能源储能的交直流新能源电网节点拓扑集合X={xs|xs∈Ω，s∈S}；

模型输出： 交直流新能源电网分区动态高阶拓扑结构先验能量Eh（X|B）。

5 仿真分析

根据东北某地区的接入分布式储能，且以风、光、 火电大规模交直流混合送出的送端电网中多能源运行数据及IEEE39 节点算例为基础， 建立多源储能与交直流电网仿真模型。 仿真系统模型如图2 所示。由图2 可见，在该系统中有6 个火电（GE） 电源、5 个风电 （WP） 电源节点、4 个光伏（PV）电源、6 个多能源储能（ES）节点，图2 中的实线为交流线路，虚线为直流线路。

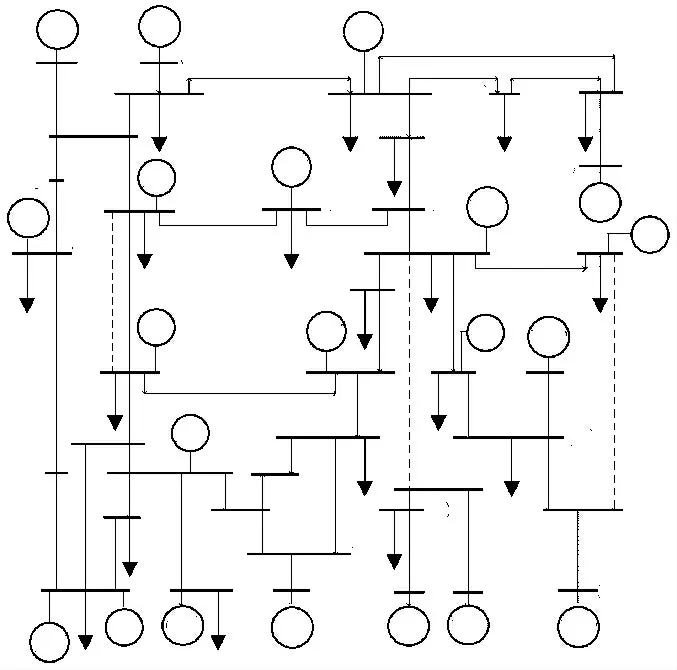
图2 含多能源储能的交直流电网结构图Fig.2 Structure diagram of AC/DC hybrid grid with multi-energy storage

图2 中交直流新能源电网负荷包括本地负荷和外送负荷。系统电源、储能和直流输电容量参数如表1 所示。

表1 交直流新能源电网参数Table 1 Parameters of new energy AC/DC hybrid grid

在交直流新能源电网中，风电、光伏、火电及本地负荷、 外送负荷的典型日变化曲线如图3 所示。 由图3 可知，在不配置储能系统时，由于电网中的新能源出力的波动特性， 当电网总负荷需求发生变化时，为满足功率平衡要求，火电机组出力必须根据总功率不平衡量进行调节。由图3 可知，可再生能源比例较高时， 会对常规火电机组造成较大的调峰压力。

图3 不配置储能时交直流电网电源和负荷曲线Fig.3 Power supply and load curve of AC/DC hybrid grid without multi-energy storage

在配置多能源储能后，新能源波动、火电出力波动、 电网总负荷及多能源储能系统总储放功率日变化曲线如图4 所示。由图4 可知，在交直流新能源电网中的多个节点配置了多能源储能后，电网总的功率不平衡量可由多源储能承担较大部分。同时，由于在负荷峰谷时刻须要协调火电机组或储能系统出力， 将可能导致与之相连的直流线路输送功率发生变化。 电网负荷峰谷差及新能源出力的反调峰特性越大， 直流功率变化的可能性也越大。

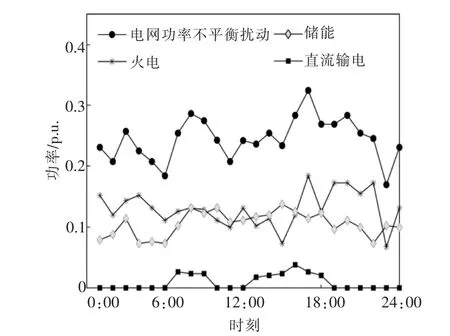
图4 含多能源储能的电网功率调节曲线Fig.4 Grid power adjustment curve of AC/DC hybrid grid with multi-energy storage

采用本文提出的交直流新能源电网动态分区协调优化算法对图2 系统的功率不平衡扰动进行分区优化控制仿真。控制参数：多能源同质化尺度参数ρ=0.33，能量越限惩罚因子γ=1.16。此时，新能源波动、火电出力波动、电网总负荷及多能源储能系统总储放功率日变化曲线如图5 所示。

图5 基于动态分区控制电网功率调节曲线Fig.5 Grid power adjustment curve of AC/DC hybrid grid with proposed dynamic partition control

由图5 可知， 在针对系统负荷波动及新能源出力波动特性采取动态分区的功率平衡策略后，原系统模型为10 个新能源节点和5 个多能源储能节点出力在能量关联度的高阶先验知识模型，采用本文所提算法能够对功率不平衡量变化进行分区协调。因此，在交直流新能源电网中相同的功率不平衡扰动下， 火电机组出力调节时间和调节容量，以及相应的直流线路功率变化时间和容量，都有较大比例的下降。

为突出本文算法优势，与文献[12]的LPV 鲁棒优化进行对比分析， 最优解的收敛曲线如图6所示。

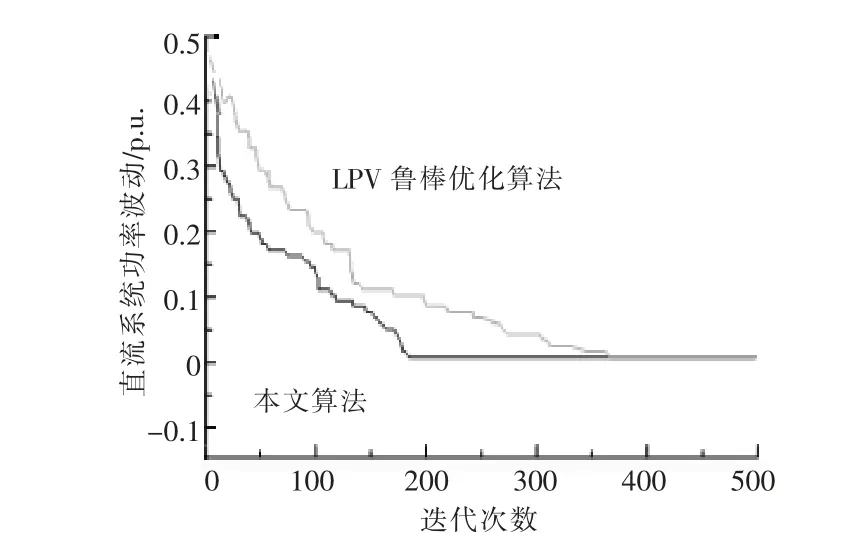
图6 不同算法收敛曲线Fig.6 Different algorithms for the best values

6 结束语

本文针对交直流新能源电网在本地和外送负荷波动与新能源出力波动下的电网功率不平衡扰动优化控制问题， 研究了考虑大规模多能源储能节点与交直流混联节点同质化尺度参数及能量交互约束的电网动态分区协调的功率平衡优化控制算法。 主要结论如下。

①对比不配置储能的交直流新能源电网，配置多源储能能够有效降低系统内可再生能源的扰动，提升交直流新能源电网的灵活性调节能力。

②基于电网节点拓扑能量相关度的电网控制分区模型， 能够在电网动态分区过程中较好地协调多源储能与交直流能量交互关系及能量同质化特性。

③基于高阶拓扑关联度先验知识模型的分区优化算法， 能够有效针对新能源与负荷波动的变化，对电网总功率不平衡实现较好的抑制。