Azimuthal Variations of the Convective-scale Structure in a Simulated Tropical Cyclone Principal Rainband

Yue JIANG, Liguang WU, Haikun ZHAO, Xingyang ZHOU, and Qingyuan LIU

1Key Laboratory of Meteorological Disaster of Ministry of Education,Nanjing University of Information Science and Technology, Nanjing 210044, China

2State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China

3Department of Atmospheric and Oceanic Sciences and Institute of Atmospheric Sciences,

ABSTRACT Previous numerical simulations have focused mainly on the mesoscale structure of the principal rainband in tropical cyclones with a relatively coarse model resolution. In this study, the principal rainband was simulated in a semi-idealized experiment at a horizontal grid spacing of 1/9 km and its convective-scale structure was examined by comparing the convective elements of the simulated principal rainband with previous observational studies. It is found that the convective scale structure of the simulated principal rainband is well comparable to the observation.

The azimuthal variations of the convective scale structure were examined by dividing the simulated principal rainband into the upwind, middle and downwind portions. Some new features are found in the simulated principal rainband. First, the overturning updraft contains small-scale rolls aligned along the inward side of the outward-leaning reflectivity tower in the middle portion. Second, the inner-edge downdraft is combined with a branch of inflow from the upper levels in middle and downwind portions, carrying upper-level dry air to the region between the overturning updrafts and eyewall, and the intrusion of the upper-level dry air further limits the altitude of the overturning updrafts in the middle and downwind portions of the principal rainband. Third, from the middle to downwind portions, the strength of the secondary horizontal wind maximum is gradually replaced by a low-level maximum of the tangential wind collocated with the low-level downdraft.

Key words: azimuthal variations, principal rainband, tropical cyclone, WRF-LES simulation

1. Introduction

A tropical cyclone (TC) usually exhibits an eyewall and a set of spiral rainbands. In the inner-core region, the spiral rainbands include one principal rainband and several secondary rainbands (Willoughby et al., 1984). The principal rainband spirals radially inward, often becoming tangent to the eyewall and displaying a variety of internal structures with deep convective cores embedded in stratiform precipitation(Atlas et al., 1963; Barnes et al., 1983, 1991; Hence and Houze, 2008; Didlake and Houze, 2009, 2013a, b). In some intense storms, spiral rainbands may evolve into a secondary eyewall (Houze, 2007; Didlake and Houze, 2011). Thus,the evolution and structure of the principal rainband are important to understanding TC intensity and structure changes.

Based on the airborne radar data of Hurricane Floyd(1981), Barnes et al. (1983) for the first time revealed the structure of an inner rainband including a radially outward leaning updraft and a descending radial inflow that transports low-equivalent potential temperature air to lower levels. Using high-resolution airborne dual-Doppler radar data of Hurricane Rita (2005) and Katrina (2005), further studies provided more details of the convective-scale structure of the principal rainband (Hence and Houze, 2008; Didlake and Houze, 2009, 2013a, b). Hence and Houze (2008) proposed a conceptual model with convective cells on the inner edge of the rainband. While convective cells are initiated at the upwind portion and collapse into a region of stratiform precipitation in the downwind portion, the middle portion of the principal rainband consists of the overturning updraft from the lower inflow layer, the low-level downdraft (LLD)from the mid-level radially outside the rainband, and the inner-edge downdraft (IED) originating in upper levels radially inward edge of the high reflectivity core. There is a secondary horizontal wind maximum (SHWM) at middle levels on the radially outward side of the overturning updraft, which may enhance the SHWM through a vertical convergence of positive vorticity. Didlake and Houze(2009) found the low-level wind maximum (LLWM) that is radially inward from the IED at 2−3 km. An LLWM at the 1.5-km level on the inner side of the rainband was also found in the composite tangential wind cross section of the principal rainband in Hurricane Floyd (1981) (Barnes et al.,1983).

Our current knowledge on the convective-scale structure of the principal rainband is based mainly on observational analysis of airborne radar data in several hurricanes.Aircraft missions require a lot of planning and resources,and they rarely occur relative to the lifetime of all storms.Numerical simulation has the potential to obtain detailed knowledge of the principal rainband. Indeed, with rapid improvements in numerical models and computational resources, the mesoscale structures of the spiral rainband can be well simulated in mesoscale numerical models(Sawada and Iwasaki, 2010; Akter and Tsuboki, 2012; Li and Wang, 2012a, b; Moon and Nolan 2015a, b; Xiao et al.,2019). For example, Moon and Nolan (2015a, b) examined the radius−height cross section through the middle and downwind region of the simulated principal rainband in a numerical simulation of Hurricane Bill (2009), with an innermost domain of 1-km horizontal grid spacing. However, the incloud turbulence could not be simulated with the 1-km Weather Research and Forecasting (WRF) model simulation. Small-scale turbulent mixing plays an important role in transporting heat, momentum and water vapor in deep convective cloud (LeMone and Zipser, 1980; Marks et al.,2008; Hogan et al., 2009; Lorsolo et al., 2010; Giangrande et al. 2013). Zhu et al. (2018) suggested that the small-scale eddy disturbance above the boundary layer in the TC eyewall and rainbands has an important influence on TC intensification. The feedback of small-scale structures may affect the convective-scale structure of the principal rainband.

The large-eddy simulation (LES) technique, in which the energy-producing 3D atmospheric turbulence in the planetary boundary layer (PBL) are explicitly resolved, has been incorporated into the Advanced Research version of the WRF model (Mirocha et al. 2010). An increasing number of TC simulations have been successfully conducted using the WRF-LES framework with horizontal grid spacing less than 1 km (Zhu, 2008; Rotunno et al., 2009; Bryan et al., 2014;Rotunno and Bryan, 2014; Stern and Bryan, 2014; Green and Zhang, 2015; Wu et al., 2018). Especially, Wu et al.(2018, 2019) suggested that the WRF-LES framework with the horizontal resolution of 37 m can successfully simulate the tornado-scale vortex in the inner edge of the TC eyewall.

Since few studies have focused on the convective-scale structure of the principal rainband simulated with the WRFLES framework, one of the two objectives of this study was to simulate the convective-scale structure of the principal rainband at a horizontal grid size of 1/9 km. Moreover, previous observational studies have focused mainly on the middle portion of the principal rainband. The other objective of this study was to examine the azimuthal variations of the convective-scale structure of the simulated principal rainband. The numerical experiment is described in section 2 and the simulated principal rainband is identified in section 3. The azimuthal variations of its convection structure are discussed in sections 4 and 5, with a focus on the convective elements of the simulated principal rainband, followed by a summary in section 6.

2. Numerical experiment

The design of the semi-idealized numerical experiment in this study was the same as that in Wu et al. (2018),except the lack of the 1/27-km resolution domain. The simulated TC evolved in the large-scale background of Typhoon Matsa (2005) from 0000 UTC 5 August to 1200 UTC 6 August, which was obtained with a 20-day low-pass Lanczos filter (Duchon, 1979). The large-scale environment was from the National Centers for Environmental Prediction Final Operational Global Analysis data. Version 3.2.1 of the WRF model was used, with the outermost domain centered at (30.0°N, 132.5°E), covering an area of 6210 × 5670 km2and containing 230 (zonal direction) ×210 (meridional direction) grid points of 27-km grid spacing. The five nested, two-way interactive domains contained 399 (zonal direction) × 432 (meridional direction),333 × 333, 501 × 501, 721 × 721 and 1351 × 1351 grid points, respectively. The corresponding horizontal resolutions were 9 km, 3 km, 1 km, 1/3 km (～333 m), and 1/9 km(～111 m). Except the 27-km and 9-km resolution domains,the other four domains were movable to follow the simulated storm. The model consisted of 75 vertical levels with a top of 50 hPa. The vertical resolution was 70−100 m below 1 km and 250−400 m above 1 km.

Except the Kain−Fritsch cumulus parameterization scheme and the WRF single-moment 3-class microphysics scheme used in the outermost domain (Kain and Fritsch,1993), the WRF single-moment 6-class microphysics scheme was used in the five nested domains with no cumulus parameterization scheme (Hong and Lim, 2006). The LES technique was adopted in the innermost two domains(Mirocha et al., 2010), while the Yonsei University PBL parameterization scheme (Noh et al., 2003) was used in the other domains. The other physics options and details of the experimental design can be referred to in Wu et al. (2018,2019).

The simulation was run over the open ocean with a constant sea surface temperature of 29°C. The domain with the resolution of 1/9 km was activated at 24 h and terminated at 51 h. The center of the simulated TC was defined with a variational approach in which the center is located until the maximum azimuthal-mean tangential wind speed is obtained(Wu et al., 2006). Our focus is on the simulated principal rainband in the innermost domain, which covers the TC inner core region with an area of 150 × 150 km2.

3. Simulated principal rainband

The simulated TC generally takes a northwest track (figure not shown). Figure 1 displays the intensity of the simulated TC in terms of maximum azimuthally averaged and instantaneous wind speeds at 10 m and the minimum sea level pressure. During the 28-h period, the azimuthal averaged maximum wind speed fluctuates around 41 m s−1,while the instantaneous maximum wind speed exhibits a slight decreasing trend. The 28-h mean instantaneous maximum wind speed is 68.4 m s−1. The minimum sea level pressure significantly decreases from 24 to 30 h, and then fluctuates around 918 hPa. The simulated radar reflectivity at 3-km altitude indicates a prominent asymmetric structure. As shown in Fig. 2, the eyewall is open at 29 h and 30 h, with the enhanced convection mainly on the southeast to northeast side. The enhanced eyewall convection is located on the left-of-shear side of the simulated TC, in general agreement with previous studies (Wang and Holland, 1996;Frank and Ritchie, 1999, 2001; Braun and Wu, 2007). In this study, the vertical wind shear is calculated as the difference of horizontal wind between 200 and 850 hPa within a radius of 500 km.

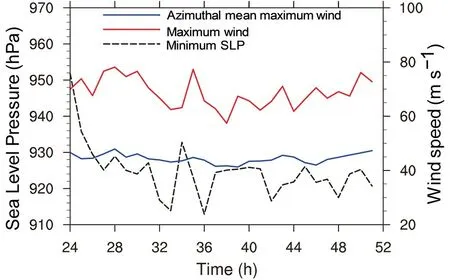
Fig. 1. Evolution of the simulated TC intensity during 24−51 h.The red (blue) line denotes the maximum instantaneous(azimuthal-mean) wind speed at 10 m. The black dashed line denotes the minimum sea level pressure.

There is a strong rainband outside the eyewall (Fig. 2).At 29 h, the simulated rainband is detached from the eyewall and located radially between 60 and 80 km on the eastern side. The northern part of the rainband becomes tangent with the eyewall at 30 h, while the secondary rainband is hard to identify. At 31 and 32 h, the rainband is again separated from the eyewall. We can see that the rainband remains at a relatively fixed position in the azimuthal direction during 29−32 h. We also examined the field of the simulated radar reflectivity at other hours and found that the rainband remains quasi-stationary in the azimuthal position relative to the TC center during the 28-h period, while the radial position varies slightly. Based on the definition of the principal rainband (Willoughby et al., 1984), the rainband can be identified as a principal rainband.

In the following discussion, we focus mainly on the convective-scale structure of the principal rainband at 29 h since the innermost domain fully covers the rainband.Figures 3−5 show the simulated radar reflectivity at 3-km altitude, the vertical motion at 5 km and rainwater mixing ratio at 4 km for the upwind (R1), middle (R2, R3) and downwind portions (R4) of the principal rainband. In the upwind portion (R1), the convective activity is dominated by isolated cells that can be identified with the radar reflectivity larger than 40 dBZ (Fig. 3a), vertical motion stronger than 2 m s−1(Fig. 4a) and enhanced rainwater mixing ratio (Fig.5a). The cellular structure is also demonstrated by the surrounding downward motion, while the downward motion is not very clear for some weak cells in Fig. 4a. The maximum updraft of 11.96 m s−1at 5-km altitude is found in the upwind convective cell.

In the middle portion (R2, R3), the isolated convective cells are replaced by band-like structures, which are oriented roughly in the radial direction. The band-like structures are clear in the field of the 5-km vertical motion stronger than 3 m s−1(Fig. 4b), while the radar reflectivity and rainwater become connected in the downwind part (R3)(Figs. 3b and 5b). The maximum updraft is 12.92 m s−1in the middle portion, slightly stronger than that in the upwind portion. Note that the radar reflectivity and rainwater in R3 become two linear structures, which are about 20 km in length and roughly along the tangential wind. Tang et al.(2018) also found similar sub-rainband structures in the principal rainband of Typhoon Hagupit (2008) when they analyzed the observational data collected during the Observing System Research and Predictability Experiment Pacific Asian Regional Campaign and Tropical Cyclone Structure 2008 experiment. They suggested that the dynamics of the sub-rainband is similar to that of squall lines.

In the downwind portion (R4), the principal rainband shows two convective bands, which are clear in the fields of radar reflectivity (Fig. 3c) and rainwater (Fig. 5c). The two convective bands contain isolated updrafts (Fig. 4c), and the radar reflectivity larger than 35 dBZ is generally connected within the sub-rainband. The maximum updraft is 8.1 m s−1,weaker than those in the upwind and middle portions. In section 4, to better demonstrate the azimuthal variations of the convective structure, we divide the rainband into four segments when constructing the composite convection-scale structure.

4. Azimuthal variations of the convectivescale structure at 29 h

In this section, the azimuthal variations of the convective structure of the simulated principal rainband are discussed in the four segments mentioned in the last section. Following previous studies (Didlake and Houze, 2009, 2011),we constructed the radial cross sections of the principal rainband in R1−R4 at 29 h. The vertical structure was composited based on the curves shown in Figs. 3−5, which were fitted based on the relatively strong updrafts. The grids with vertical motion larger than 4, 5 and 3 m s−1were first selected for the upwind (R1), middle (R2, R3) and downwind (R4) segments, respectively, and then three different polynomial curves were fitted for the different parts. The variables were composited at an azimuthal interval of 0.5° in the radius−height plane. The cross sections averaged over R1,R2, R3 and R4 at 29 h were based on 51, 51, 71 and 71 profiles, respectively. Each cross section is centered at the fit-ting line and extends 30 (10) km radially inward (outward)from the fitting line.

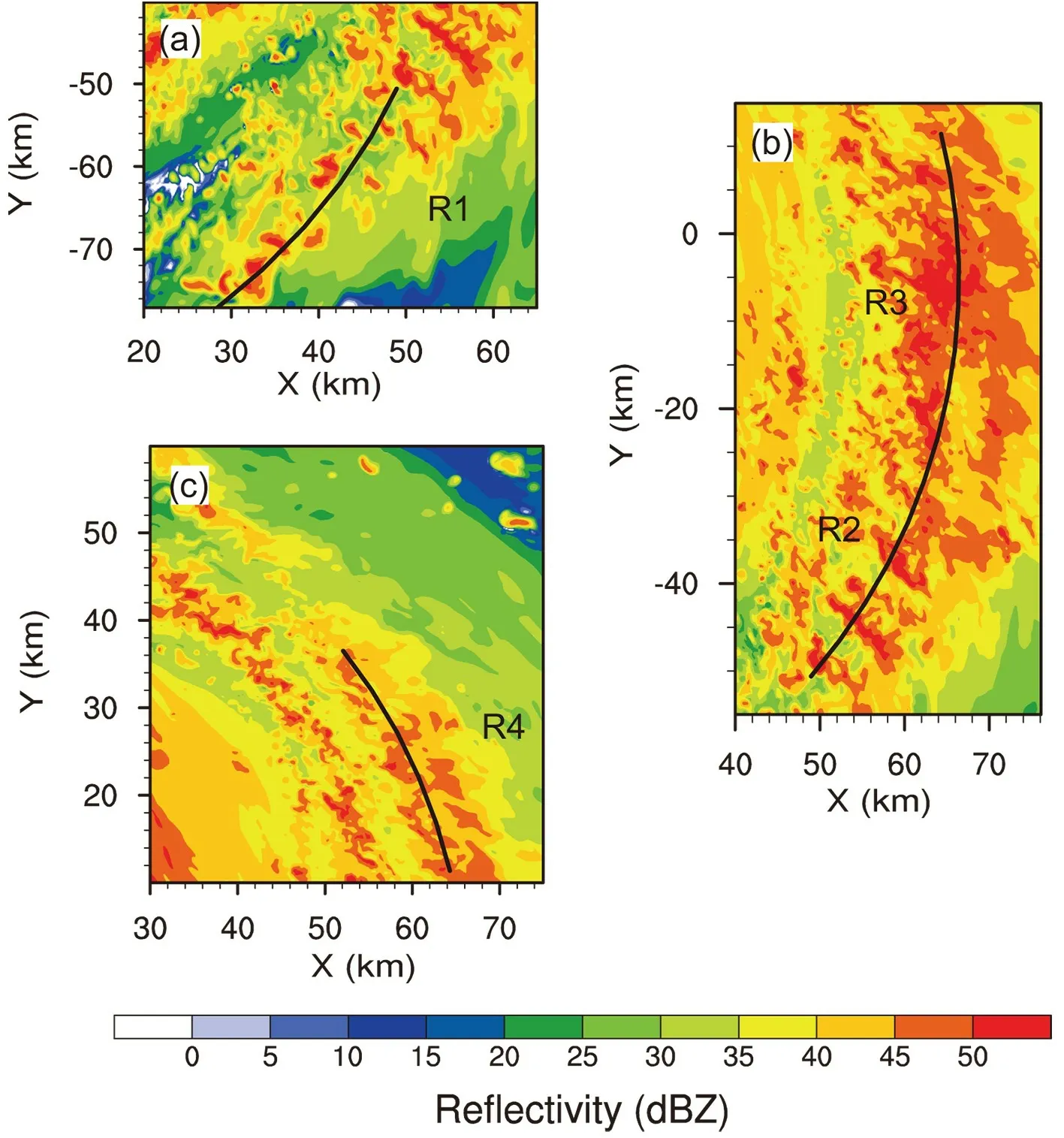
Fig. 3. The 3-km simulated radar reflectivity (unit: dBZ) in the (a) upwind, (b) middle and (c)downwind portions of the principal rainband at 29 h. The polynomial curves are fitted based on the distribution of vertical velocity at 5-km altitude.

4.1. Overturning updraft

Figures 6a−d show the composited cross sections of upward vertical motion and simulated radar reflectivity.Note that part of the TC eyewall is indicated by the strong vertical motion and enhanced radar reflectivity on the far-left side. In the upwind part (R1), the overturning updraft can be identified by the strong vertical motion below 6 km radially between −5 km and 0 km, and lies in the inner edge of the reflectivity tower (Fig. 6a). The updraft and reflectivity tower lean radially outward slightly. In R2, however, there are three maxima in the upward motion, indicating three distinct updrafts. The tallest updraft is radially between −5 km and 10 km, reaching the altitude of about 8 km with the strongest vertical motion at about 4 km. Compared to the updraft in R1, the tallest updraft in R2 further tilts in the vertical and is in the inner edge of the reflectivity tower (Fig.6b). The other two maxima on the radially inward side of the strongest updraft are accompanied by the separate reflectivity towers. The altitudes of these two updrafts decrease radially inward.

As the principal rainband spirals close to the TC eyewall (R3 and R4), the stratiform precipitation increases, and the individual reflectivity towers merge into a single tower(Figs. 6c and d). There are multiple enhanced updrafts that are aligned along the inward side of the outward-leaning reflectivity tower. The strongest one is tallest and reaches about 6 km, lower than that in R2. Although the overturning updraft in the conceptual model is indicated by a strong updraft associated with a single convective cell (Hence and Houze, 2008; Didlake and Houze, 2009), we can see that the overturning updrafts actually consist of a series of small-scale structures that are aligned along the inward side of the outward-leaning reflectivity tower.

In order to demonstrate the small-scale structures, we calculated the perturbation wind fields by removing the 3-km running average. Figure 7 shows the 3D structure of the perturbation wind field in R2. We can see three rolls embedded in the overturning updraft, indicated by the 3-km mean vertical motion on the background. Their vertical and radial scales are 1−2 km with downward drafts on the radially inward side. As shown in Fig. 6, the 3-km mean vertical velocity along the inward side of the outward-leaning reflectivity tower generally increases radially outward. We think that the horizontal rolls may be associated with the radial shear of the vertical motion and the vertical shear of the radial motion. Didlake and Houze (2009) found that the overturning updraft of the principal rainband of Hurricane Katrina (2005) reached a maximum speed of over 4 m s−1between 3- and 5-km altitude. In our simulation, the maximum speed of the updrafts is about 3 m s−1at similar altitude. Considering that the azimuthal average was removed in the current analysis, the simulated overturning updrafts are consistent in magnitude with the observation in Didlake and Houze (2009).

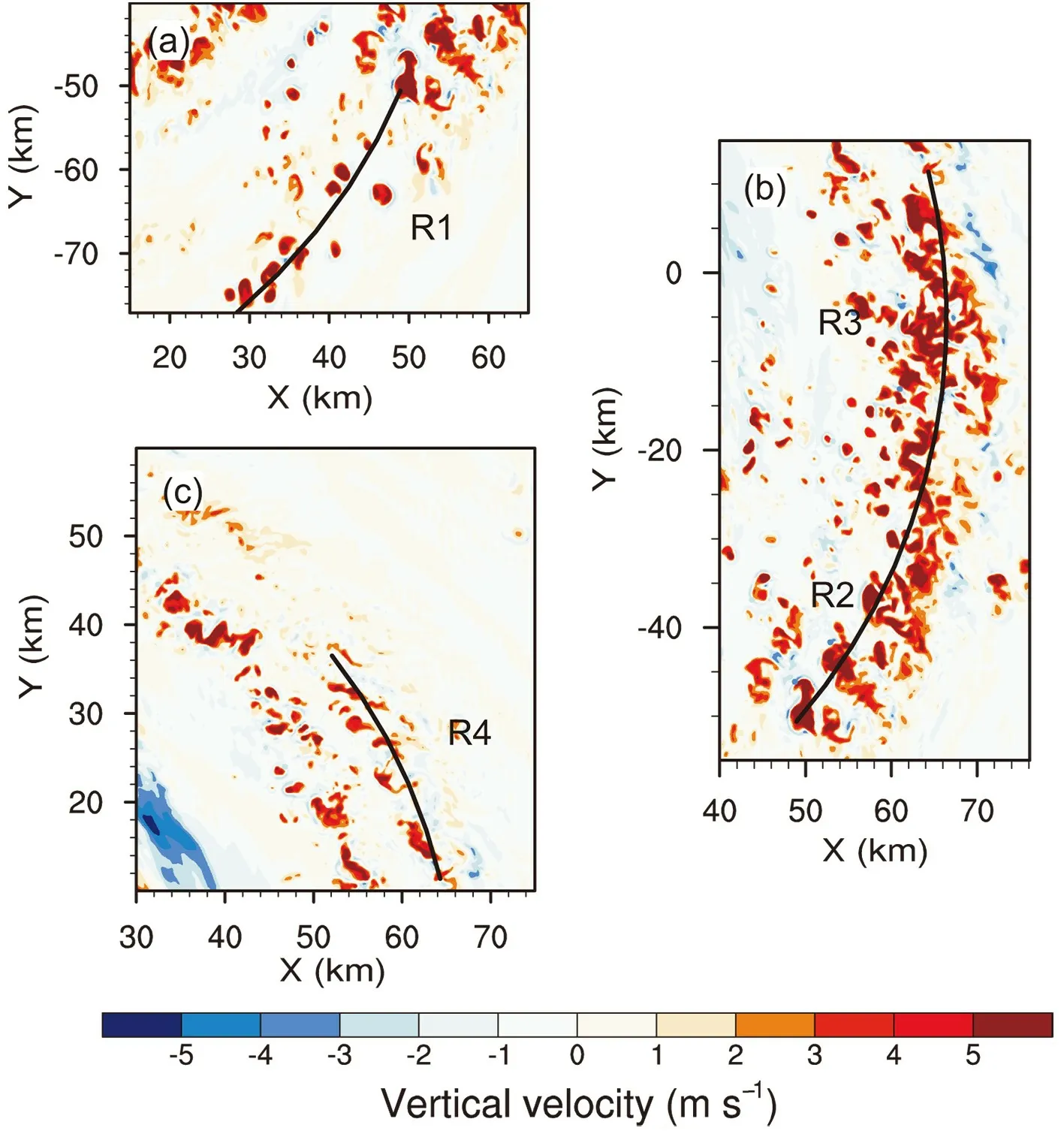
Fig. 4. The 5-km vertical velocity (units: m s−1) in the (a) upwind, (b) middle and (c)downwind portions of the principal rainband at 29 h. The polynomial curves are fitted based on the distribution of vertical velocity.

The small-scale perturbation in the principal rainband can be further examined by calculating the turbulent kinetic energy (TKE) at 29 h. The calculation of TKE was based on the perturbation wind fields by removing the 3-km running average. Following Lorsolo et al. 2010, it can be written as u′v′w′

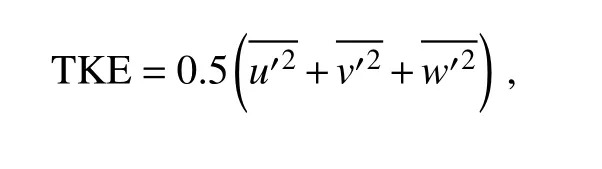
where , , and are the perturbation wind components.

Figure 8a shows the horizontal distribution of TKE at 5-km height. While the large TKE in the eyewall is associated with extreme updrafts (Zheng et al., 2020), there is large TKE in the principal rainband, indicating the presence of small-scale structures. Figure 8b shows the vertical profile of the TKE averaged over the region in Fig. 7. The cross sections are averaged with 26 profiles at an interval of 0.2°. There are three TKE maxima corresponding to the small-scale structures in Fig. 7.

4.2. IED

Hence and Houze (2008) were the first to detect the IED in Hurricanes Katrina (2005) and Rita (2005). The principal rainband was bounded by a strong downdraft that originated at upper levels. They suggested that the sharp inner-edge reflectivity gradient was due to the presence of the IED. Didlake and Houze (2009) further demonstrated that the IED originating between the altitudes of 6 and 8 km was forced aloft by pressure perturbations formed in response to the adjacent buoyant updrafts and the negative buoyancy associated with the evaporative cooling from the rainband precipitation.

Fig. 5. The 4-km rainwater mixing ratio (units: g kg−1) in the (a) upwind, (b) middle and (c)downwind portions of the principal rainband at 29 h. The fitting curves are the same as in Fig. 4.

Figures 6e−h show the composited downward motion and radar reflectivity for R1−R4. The most intense downward motion in R1 lies radially between −15 km and −20 km,with the maximum at 4-km altitude (Fig. 6e). The downdraft is about 15 km away from the strongest updraft shown in Fig. 6a. From R1 to R4, the downdraft leaning radially outward extends in length and increases in strength,reaching its peak strength in R3 and R4. As indicated in Hence and Houze (2008) and Didlake and Houze (2009),the strong outward-leaning downdraft tops the overturning updrafts and limits their altitude.

The IED can be further seen in the cross section of the vectors of radial and vertical motions (Fig. 9). Note that the symmetric components of the radial and vertical motions relative to the TC center have been removed. Due to the relatively weak downward motion, the contours of downward motion are also plotted in this figure. In the upwind part(R1), the strong IED below the outflow from the TC eyewall is associated with a circulation with the upward branch in the expanded eyewall convection. It is suggested that the downdraft is induced by the eyewall convection rather than the convection of the principal rainband. From R1 to R4, as the rainband gradually spirals close to the eye convection,the downdraft intensifies and extends from the surface to about 10 km.

In addition, the strong IED is combined with a branch of inflow from the upper levels in R3 and R4 (Figs. 9c and d). The cross section of relative humidity indicates that the inflow carries upper-level dry air to the region between the overturning updrafts and eyewall (figure not shown). The intrusion of upper-level dry air strengthens the downdraft in the downwind portion of the principal rainband. Based on numerical experiments, Li et al. (2015) suggested that the upper-level intrusion of relatively dry air may enhance the sublimation of ice particles in the upper-level outflow.While previous studies have suggested that the vertical tilt and extent of the overturning updraft are generally limited by the TC outflow (Hence and Houze, 2012; Didlake and Houze, 2013a; Zagrodnik and Jiang, 2014), as shown in Fig. 9,this study indicates that the intrusion of dry air associated with the upper-level inflow further limits the altitude of the overturning updraft in the downwind part of the principal rainband.

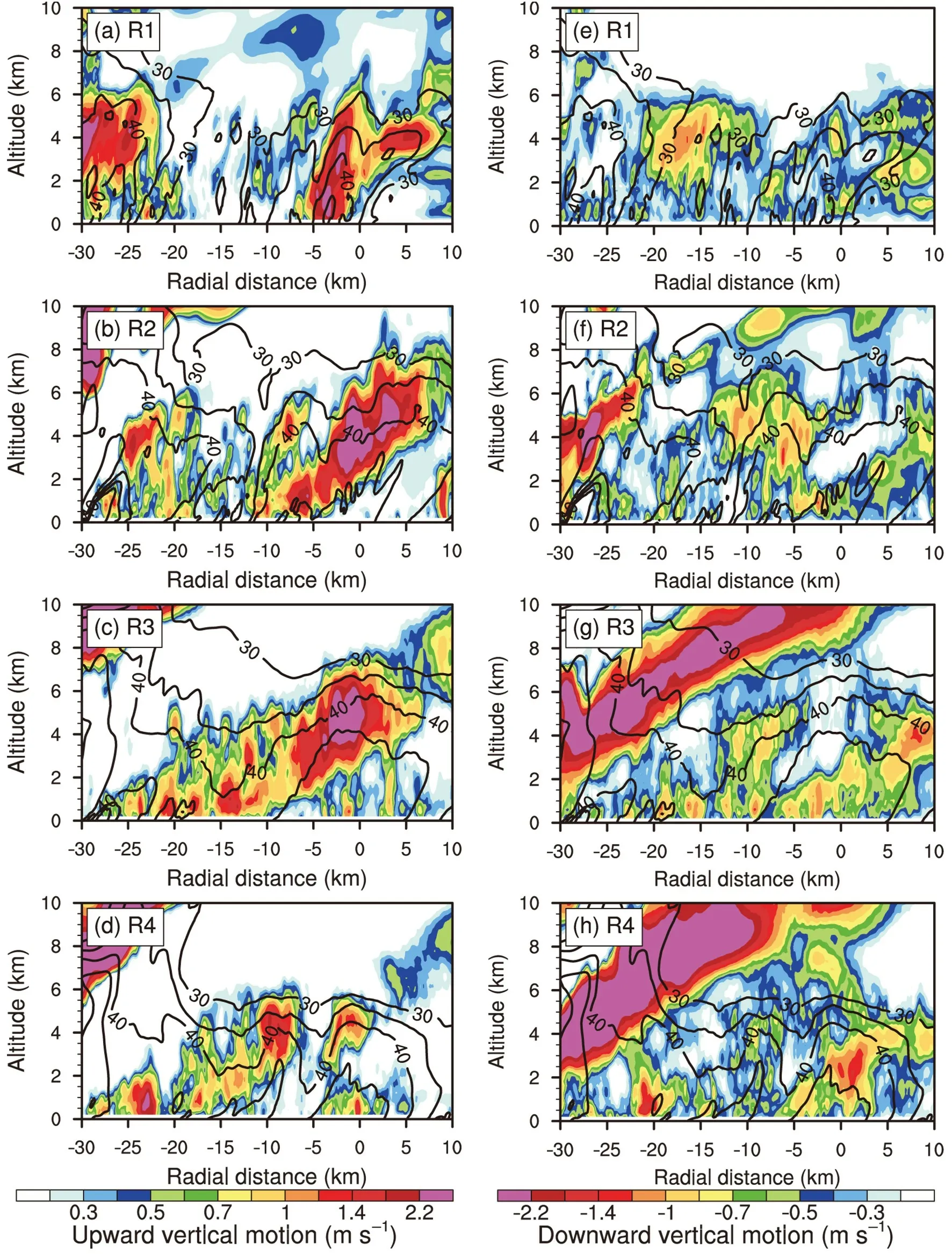
Fig. 6. (a−d) Composited radius−height cross section of upward vertical motion (shaded; units: m s−1) and radar reflectivity (contours; unit: dBZ) at 29 h, no less than 30 dBZ, at intervals of 5 dBZ. (e−h) As in (a−d) but for downward vertical motion (shaded; units: m s−1). Each cross section is centered at the fitting line extending 30 (10)km radially inward (outward).

4.3. LLD

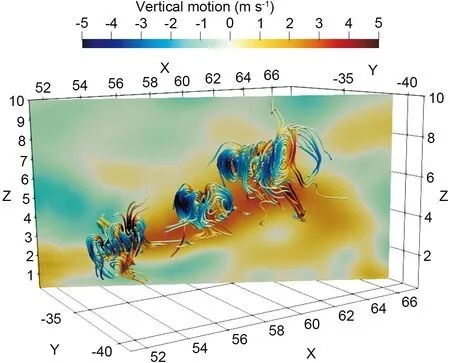
Fig. 7. The 3D streamlines of the perturbation wind. The vertical cross section of the 3-km running mean of vertical motion is in the background.The warm and cold colors in the shading and streamlines indicate the upward and downward vertical motion, respectively. The x-axis and y-axis indicate the distance (km) from the TC center, and the z-axis indicates the altitude(km) from sea level.

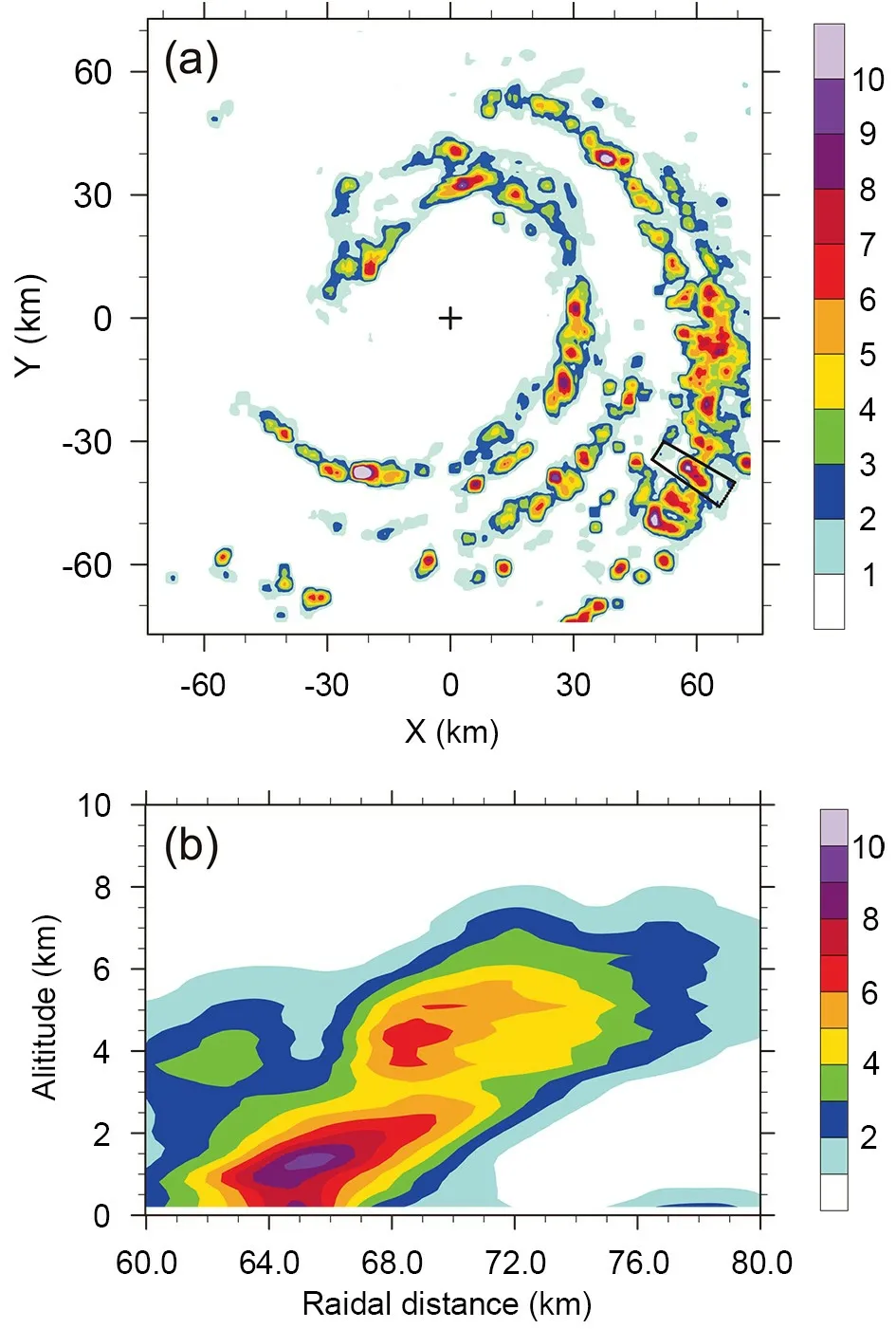
Fig. 8. (a) The 5-km TKE (units: m2 s−2) at 29 h. (b) Radius−height cross section of TKE (units: m2 s−2) composited with intervals of 0.2° in the box in (a). The box covers the region in Fig. 7.

The LLD below the overturning updraft was revealed in previous studies (Barnes et al., 1983; Hence and Houze,2008; Didlake and Houze, 2009). In conceptual models(Barnes et al., 1983; Hence and Houze, 2008), the LLD originates at 2−4 km within the heavy precipitation of the principal rainband and is driven by the precipitation drag. As shown in Figs. 6e−h, the main features of the simulated LLD are generally consistent with previous studies (Barnes et al., 1983; Hence and Houze, 2008; Didlake and Houze,2009), although the maximum downward motion of 1.3 m s−1in the LLD is weaker than that in Didlake and Houze(2009). The LLD can be clearly identified in the middle and downwind parts (R2−R4) of the principal rainband. The LLD originates at 2−4 km and descends to the boundarylayer inflow, entering the rainband on its radially outward side (Fig. 9).

Previous studies have suggested that the LLD has the potential to lower the moist static energy of the flow in the boundary layer (Barnes et al., 1983; Powell, 1990a, b). Figure 10 shows the cross sections of equivalent potential temperature and asymmetric equivalent potential temperature from R1 to R4. While there is a large area of low equivalent potential temperature between the eyewall and the overturning updrafts where the IED lies, the LLD is also associated with the equivalent potential temperature less than 352 K. The equivalent potential temperature in the boundary inflow is generally above 352 K. It is indicated that the low equivalent potential temperature mixes with the boundary-layer inflow air.In addition, in Figs. 6e−h and Figs. 6a−d we can see smallscale features in the LLD and the boundary-layer inflow. As shown in Fig. 10, the environment is convectively unstable below the LLD. Since the LES technique was incorporated in the numerical experiment, it is suggested that the smallscale features can be simulated when the horizontal and vertical resolution are about 100 m.

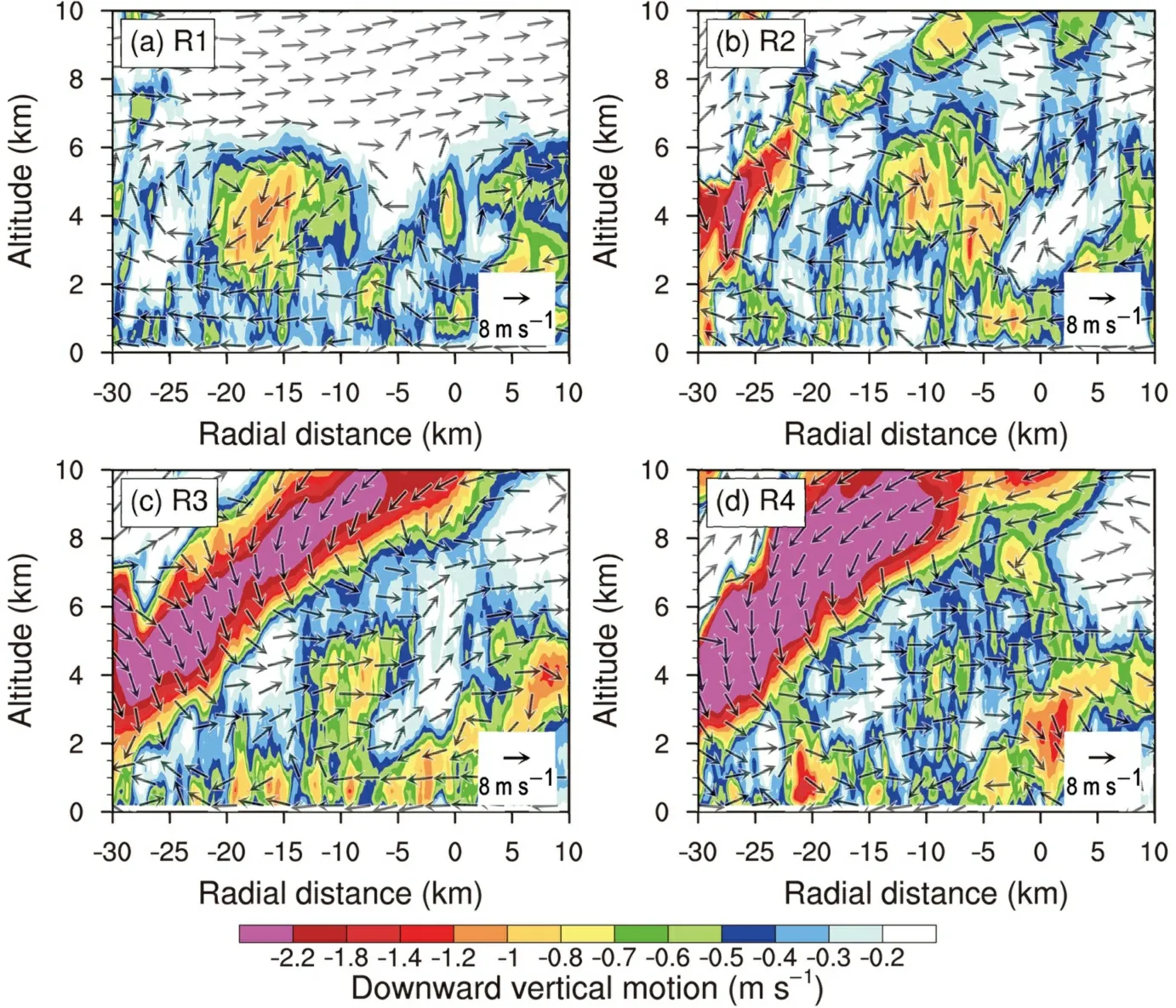
Fig. 9. (a−d) Composited radius−height cross section of downward motion (shaded; units:m s−1) and the field of asymmetric radial and vertical velocities (vectors; units: m s−1) at 29 h. Each cross section is centered at the fitting line extending 30 (10) km radially inward(outward).

Fig. 10. (a−d) Composited radius−height cross section of asymmetric equivalent potential temperature (shaded; unit: K) and equivalent potential temperature (contours; unit: K) at 29 h, no less than 350 K, at intervals of 2 K. Each cross section is centered at the fitting line extending 30 (10) km radially inward (outward).

4.4. SHWM

Previous observational studies have indicated that the principal rainband is associated with a mid-level wind maximum or the SHWM (Samsury and Zipser, 1995; Hence and Houze, 2008). Ryan et al. (1992) found that such an SHWM was associated with the rainband within a developing storm,and Barnes and Stossmeister (1986) indicated that the SHWM dissipated along with the convection within a decaying rainband. To illustrate the features of the tangential wind in the principal rainband of the simulated TC, we first removed the symmetric component of the tangential wind and then plotted the radial−height cross sections averaged over the four segments (Fig. 11).

As shown in Fig. 11, enhanced tangential wind at about 4 km can be found in all four segments, and it reaches a maximum of about 5 m s−1in R2. Compared to Fig. 6, the enhanced tangential wind is generally collocated with the overturning updrafts. In agreement with the conceptual model in Hence and Houze (2008), careful examination indicates that the SHWM shifts radially outward slightly, relative to the most intense vertical motion in Fig. 6. In the downwind part (R3 and R4), however, the strength of the midlevel wind maximum decreases and the SHWM is replaced by a low-level maximum of the tangential wind. Although Didlake and Houze (2013a) also mentioned the difference of the mid-level tangential jet in the outer rainband and lowlevel tangential jet in the inner rainband, the altitude change in this study occurs azimuthally in the same rainband. The LLWM is collocated with the LLD, which was not found in previous studies. In our simulation, the LLWM associated with the IED, as suggested by Didlake and Houze (2009), is not found.

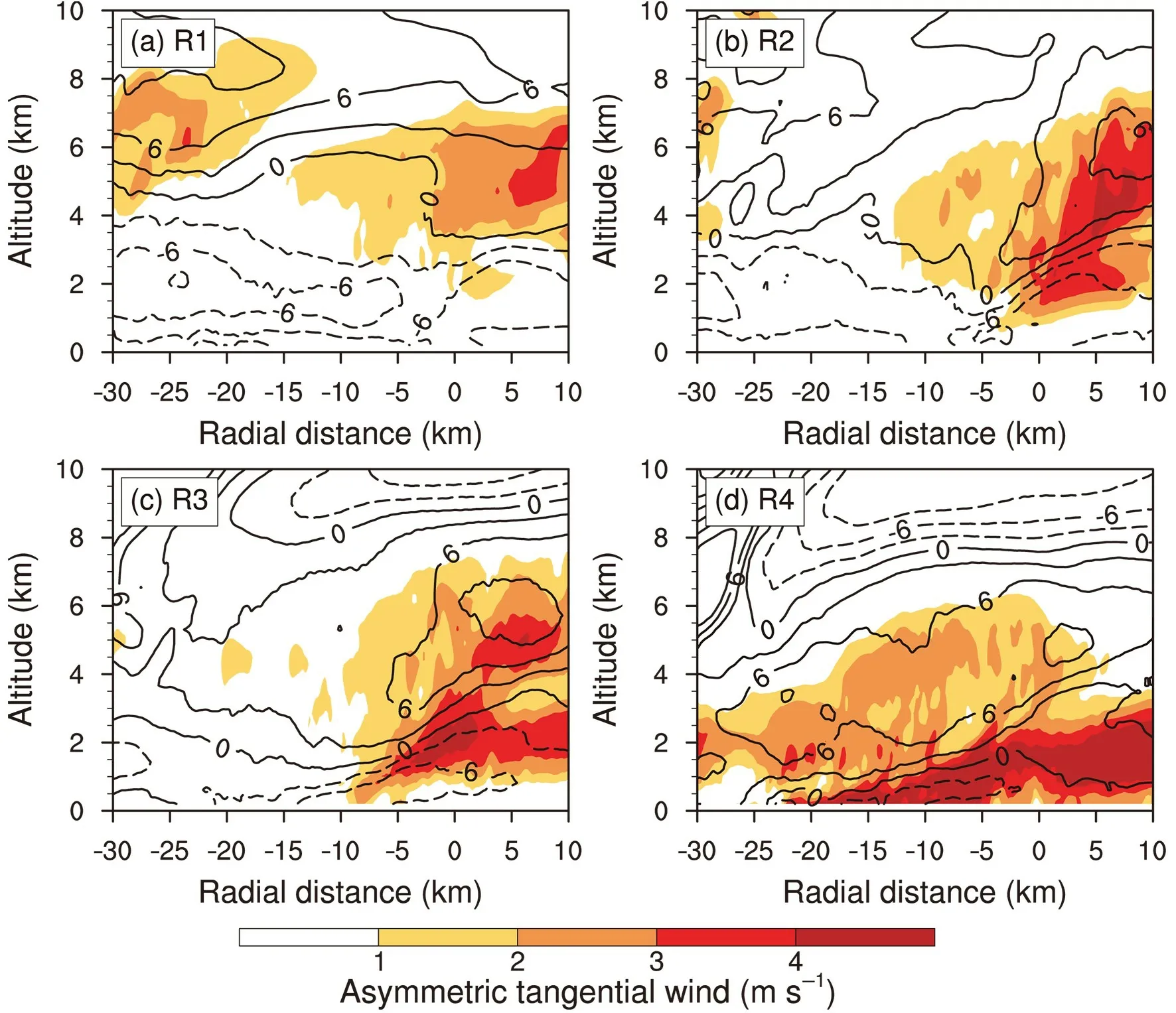
Fig. 11. (a−d) Composited radius−height cross section of asymmetric tangential wind (shaded; units: m s−1),asymmetric radial wind at intervals of 3 m s−1 (contours; units: m s−1), and radial velocity with dashed (solid)contours indicating inflow (outflow), at 29 h. Each cross section is centered at the fitting line extending 30 (10) km radially inward (outward).

Barnes et al. (1983) suggested that the low-level radial inflow slowed in the rainband and argued that the rainband may provide a barrier to the moist inflow to the storm.Although the azimuthal average has been removed, the radial inflow in the boundary can be found in Fig. 11. It reaches a peak in R2 as the overturning updrafts are strongest. The depth of the inflow layer is thicker in the upwind part than in the downwind part. As the depth of the inflow layer decreases, the speed of the inflow also decreases. It is suggested that the rainband can provide a barrier to the moist inflow to the eyewall of the simulated TC.

5. Azimuthal variations of the convectivescale structure at 31 h

To confirm the features of the convective-scale structure, we further applied the same analysis method to the simulated principal rainband at 31 h and 32 h. Since the features revealed in the principal rainband at 31 h and 32 h are generally similar to those at 29 h, a brief analysis for 31 h is presented in this section. Figure 12 shows the simulated radar reflectivity at 3-km altitude along with the vertical motion at 5 km for the middle (R2, R3) and downwind portions(R4) of the principal rainband at 31 h. Since the upwind portion is not fully covered by the innermost model domain,the following analysis is based only on the middle and downwind parts of the simulated principal rainband. As shown at 29 h, there are also two sub-bands indicated by the relatively high radar reflectivity and strong upward vertical motion. The sub-band on the inner (outer) side is stronger in R2 (R3). The fitting lines are shown in Fig. 12 and the profiles are composited with 96, 46 and 56 profiles for R2, R3,and R4, respectively.

The overturning updraft is indicated by the strong upward motion below 8 km radially between −15 km and 5 km in the middle part (R2, R3) (Figs. 13a and b). There are maxima stronger than 1.8 m s−1in the overturning updraft,indicating the presence of small-scale structures in the outward-leaning overturning updraft. From the middle portion to the downwind portion, the altitude of the overturning updraft decreases to 6 km (Fig. 13c). The IED is located below 4-km height between −15 and −10 km in R2 (Fig.13d). As the principal rainband spirals close to the TC eyewall, the upper-level downdraft occurs between the altitudes of 8 and 10 km in R3 (Fig. 13e). The upper-level downdraft is combined with the dry inflow in R4 (Fig. 13f),implying an influence on the altitude of the overturning updraft. The LLD can also be identified from the downward motion (Figs. 13e and f), although the LLD on the outer side of the reflectivity tower is not as strong as that at 29 h.

The composited cross section of equivalent potential temperature and asymmetric equivalent potential temperature at 31 h is shown in Fig. 14. The low equivalent potential temperature on the inner and outer sides corresponds to the location of the IED and LLD, respectively, while the high equivalent potential temperature corresponds to the overturning updraft. The enhanced tangential wind with a maximum of about 2.6 m s−1associated with the principal rainbandoccurs at the middle level in R2 (Fig. 15), while the enhanced tangential wind with a maximum of about 2.5 m s−1lies below 1 km height in R4. From the middle to downwind portion of the principal rainband, the SHWM is replaced by the low-level tangential wind jet. Note that the strength of the asymmetric tangential wind jet at 31 h is weaker than that at 29 h.

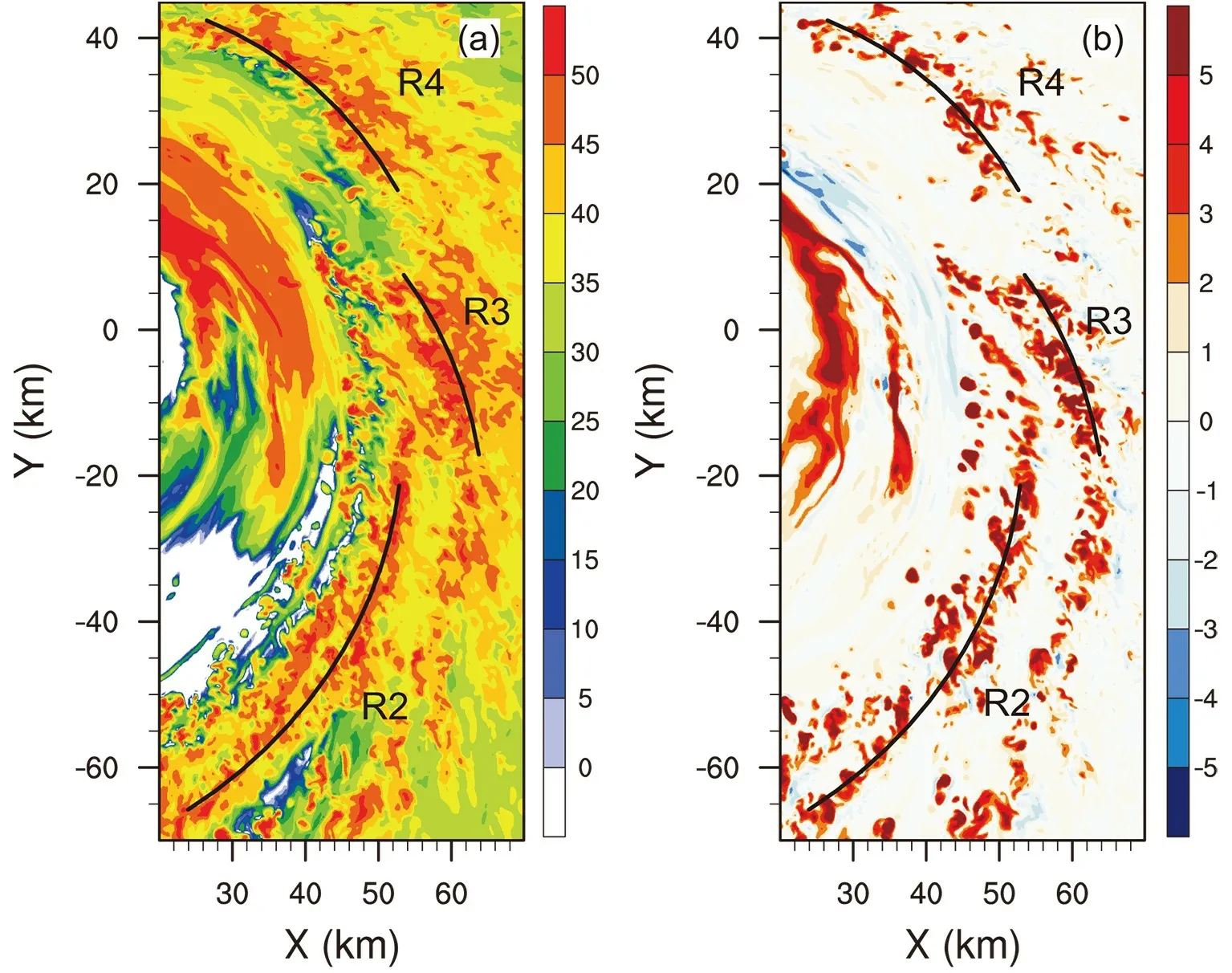
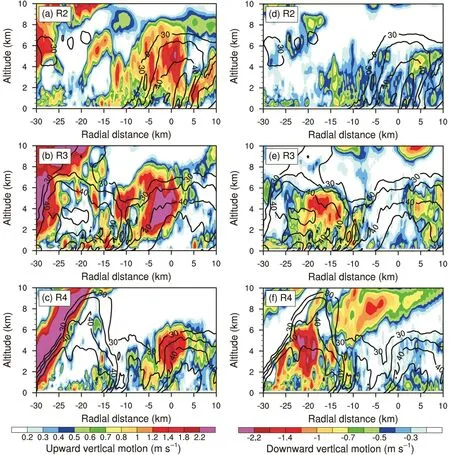
Fig. 13. (a−c) Composited radius−height cross section of upward vertical motion (shaded; units: m s−1) and radar reflectivity(contours; unit: dBZ) at 31 h, no less than 30 dBZ, at intervals of 5 dBZ. (d−f) As in (a−c) but for downward vertical motion(shaded; units: m s−1). Each cross section is centered at the fitting line extending 30 (10) km radially inward (outward).

6. Summary

While previous numerical simulations have focused mainly on the mesoscale structure of the principal rainband with a relatively coarse model resolution (Sawada and Iwasaki, 2010; Akter and Tsuboki, 2012; Li and Wang, 2012a,b; Moon and Nolan, 2015a, b; Xiao et al., 2019), the principal rainband was simulated in a semi-idealized experiment with the WRF-LES framework at a horizontal resolution of 1/9 km in this study and its convective-scale structure was examined by comparing the convective elements of the simulated principal rainband with previous observational studies (Barnes et al., 1983, 1991; Hence and Houze,2008; Didlake and Houze, 2009, 2013a, b). It was found that the convective-scale structure of the simulated principal rainband compares well to observations.

The azimuthal variations of the convective-scale structure of the simulated principal rainband were examined by dividing the principal rainband into upwind, middle and downwind portions. As shown schematically in Fig. 16, some new features were found in the simulated principal rainband:

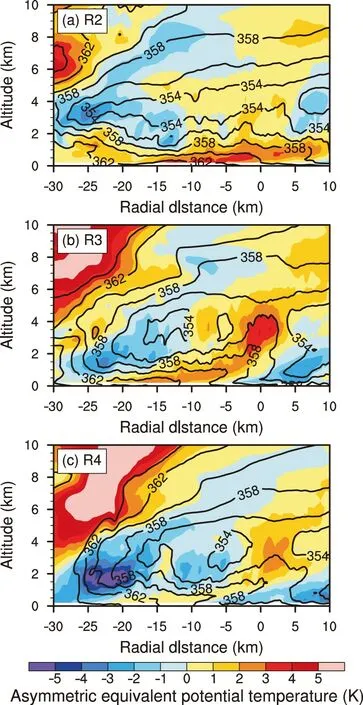
Fig. 14. (a−c) Composited radius−height cross section of asymmetric equivalent potential temperature (shaded; unit: K)and equivalent potential temperature (contour; unit: K) at 31 h,no less than 350 K, at intervals of 2 K. Each cross section is centered at the fitting line extending 30 (10) km radially inward (outward).

Small-scale rolls are embedded in the overturning updraft, which are aligned along the inward side of the outward-leaning reflectivity tower in the middle portion. The small-scale rolls with vertical and radial scales are 1−2 km.

The IED is combined with a branch of inflow from the upper levels in the middle and downwind portions. The inflow carries dry air from upper levels to the region between the overturning updraft and eyewall. The intrusion of upper-level dry air further limits the altitude of the overturning updraft in the middle and downwind portions of the simulated principal rainband.

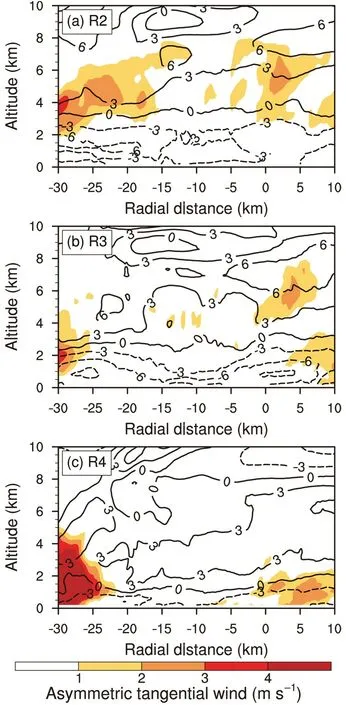
Fig. 15. (a−c) Composited radius−height cross section of asymmetric tangential wind (shaded; units: m s−1), asymmetric radial wind at intervals of 3 m s−1 (contours; units m s−1), and radial velocity with dashed (solid) contours indicating inflow(outflow), at 31 h. Each cross section is centered at the fitting line extending 30 (10) km radially inward (outward).

From the middle to downwind portions, the strength of the SHWM is gradually replaced by a low-level maximum of tangential wind, which is collocated with the LLD.Small-scale features below the LLD were simulated in the experiment.

In addition, the horizontal and vertical model resolutions were relatively too coarse to resolve the small-scale structures embedded in the overturning updraft and the boundary inflow. The convective-scale structure simulated in this experiment needs to be further verified when more observa-tional data become available.

Acknowledgements.The authors thank Prof. Ping ZHU of Florida International University for aiding with the WRF-LES framework. The authors also thank Prof. A. C. DIDLAKE of Pennsylvania State University and the anonymous reviewers for providing constructive comments. This research was jointly supported by the National Basic Research Program of China (Grant No.2015CB452803), the National Natural Science Foundation of China (Grant Nos. 41730961, 41675051, 41675009, 41675072,41922033 and 41905001), and the Open Research Program of the State Key Laboratory of Severe Weather (Grant No. 2019LASWA02).