基于增强重引力搜索的高维数据协同聚类算法

桑 遥 尹 君 王 迪 王 皓 景 康

1(国网新疆电力有限公司乌鲁木齐供电公司 新疆 乌鲁木齐 830002) 2(新疆电力有限公司信息通信公司 新疆 乌鲁木齐 830018)

0 引 言

聚类处理将物理或抽象的数据对象按指定的相似性度量归纳，是没有先验知识情况下的一种重要数据挖掘技术[1]。现有的聚类技术按采用的基本思想主要可分为4类[2]，即层次聚类算法、分割聚类算法、机器学习的聚类算法和高维数据聚类算法。层次聚类算法将数据组织成若干类构成一个树状结构来进行聚类处理。分割聚类算法首先将数据点集划分为若干个子集，再通过控制策略对各个子集分别做聚类优化处理。机器学习的聚类算法[3]主要采用人工神经网络、进化学习等理论处理聚类问题，通过机器学习的自学习能力对聚类准则进行优化处理。高维数据的特征空间中存在大量的不相关属性[4]，且高维数据间的分界较为模糊，因此高维数据的聚类处理需要结合降维处理[5]、子空间聚类[6]或协同聚类处理[7]等。

协同聚类[8-9]处理是高维数据聚类领域的一种有效方案，协同聚类对数据点和特征集同时进行聚类，以特征子集引导数据点的聚类过程，能提高聚类的效率和准确率。协同聚类技术能够提高对高维数据的聚类效果[10-11]，因此本文采用协同聚类技术解决高维数据聚类的问题。重引力搜索能够高效地解决某些特定情况下的优化问题，尤其对于高维优化问题具有独特的优势[12]，因此本文采用重引力搜索解决高维数据的聚类问题。针对重引力搜索存在局部开发能力不足的问题，本文设计拟牛顿法的局部开发策略，提高重引力搜索的求解质量。

1 协同相似性的问题模型

首先以一个实例介绍协同相似性的问题模型。表1是一个矩阵实例，图1是表1对应的二部图。理想情况下，d1-d3为第1行，d4-d5为第2行，c1-c3为第1列，c4-c6为第2列。假设一个文档为d1，且d1与d2相似，但与d3不相似，而d2与d3关于c3相似。列c1和c3均存在于d2中，因此c1与c3相似。根据二部图可推导出d1和d3间的相似性路径：d1→c1→d2→c3→d3。设Rij和Cij分别表示目标i、j间的相似性和列i、j间的相似性，相似性路径改写为d1→Cij→d3。因此协同相似性矩阵具有以下属性：如果列相似，那么包含该列的行也相似；如果行相似，那么该行的列也相似。

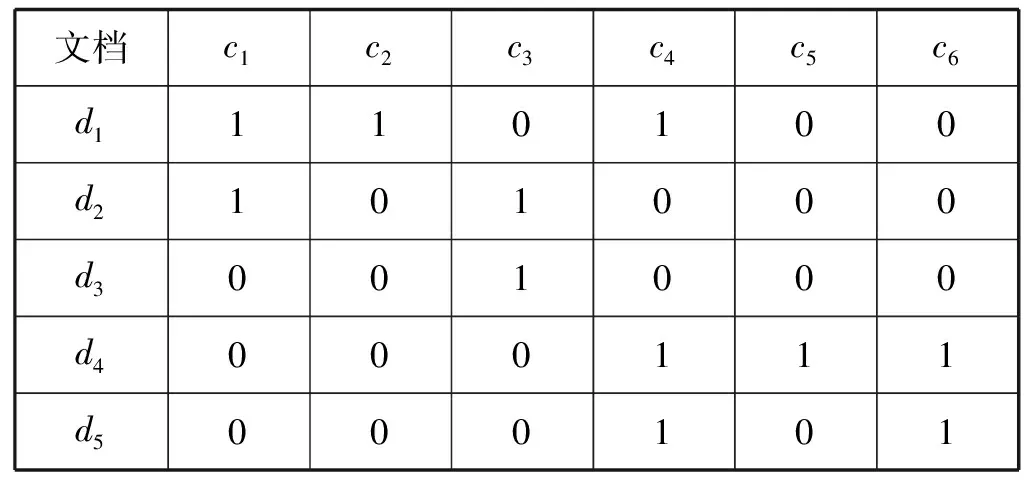
表1 一个矩阵的实例

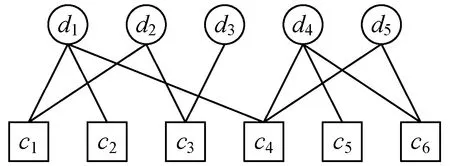
图1 表1实例的二部图结构

采用Chi-Sim[13]度量相似性。设n×n的矩阵R和m×m的矩阵C分别表示行间相似性和列间相似性。开始阶段样本或特征的相似性为未知信息，因此将R和C初始化为单位矩阵，即R=In×n和C=Im×m。算法迭代更新R和C，设R(i)和C(i)分别表示迭代i次的矩阵R和C，更新R(i)和C(i)的方法分别为：

(1)

(2)

式中:DR和DC分别为矩阵D归一化的行和列，DR和DC均采用“L1范数”做归一化处理。考虑稀疏数据行向量和列向量不等的情况，观察式(1)和式(2)，根据列(特征)相似性矩阵更新行(样本)相似性矩阵，样本间的相似性以特征相似性为参考，所以该矩阵为协同相似性矩阵。文中计算R和C的迭代次数设为3。

2 增强的重引力搜索算法(GSA)

GSA的广义目标问题为：

(3)

式中:x∈Rm为决策变量的向量；l和u均为m维的向量，分别为问题的下界和上界；f(x)为连续的目标函数。

2.1 重引力搜索算法

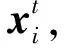
(4)

式中：N为种群规模。

GSA每次迭代更新粒子的位置和速度以提高目标函数的值，最终获得全局最优的适应度。最优函数定义如下：

(5)

最差函数定义为：

(6)

每个粒子具有引力质量和惯性质量Mi，引力质量包括主动引力质量Ma和被动引力质量Mp。粒子质量间的关系如下：

Mai=Mpi=Mii=Mii=1,2，…,N

(7)

引力质量和惯性质量分别定义为：

(8)

(9)

每次迭代个体i和j间的作用力定义如下：

(10)

式中：Fij为j对i的引力；Mpi为对i的被动引力；Maj为对j的主动引力；Rij为i和j的欧氏距离；参数ε为一个极小的常量，作用是防止分母为0；Gt为引力常量。引力常量随着迭代递减：

(11)

式中：G0为初值；α为学习速度；T为最大迭代次数。式(11)的作用是平衡搜索和开发的关系，开始阶段增强搜索能力，结束阶段增强开发能力。

粒子i受到的总作用力为所有其他个体的作用力之和，定义如下：

(12)

式中：randj为区间(0,1)的均匀随机数。为了平衡局部开发和全局搜索，仅考虑Kopt粒子的力作用于其他的粒子，Kopt关于t的函数记为Koptt=Kopt(t)。

计算每个粒子对其他粒子的总作用力，然后根据牛顿第二引力计算每个粒子的加速度，根据总作用力更新粒子的位置和速度。粒子i的加速度定义为：

(13)

更新后的速度和位置分别计算为：

(14)

(15)

GSA中粒子向高质量的粒子移动，Gt和Koptt控制局部开发和全局搜索的平衡。

2.2 基于拟牛顿法的局部开发机制

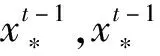
(16)

(17)

设计以下两条优质区域的判断规则：

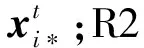
图2 R1规则和R2规则的处理示意图

拟牛顿法[14]的起点设为yk，建立二次模型目标函数：

mk(x)=f(yk)+▽f(yk)T(x-yk)+

(18)

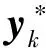
(19)

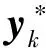
(20)

在dk方向远离yk会导致目标函数降低，因此采用以下的线性搜索方法：

(21)

为了确定合适的步长，计算式(21)的近似解，获得新点yk+1=yk+αkdk，然后从点yk+1重复程序。

引力搜索中Bk=▽2f(yk)，▽2f(yk)为f对yk的Hessian矩阵，牛顿法的收敛速度为二次方，但计算▽2f(yk)的复杂度较高，拟牛顿法能够加快计算速度。通过观察f(y)和▽f(y)的行为近似Hessian矩阵，拟牛顿法通过更新公式(Broyden Fletcher Goldfarb Shanno,BFGS)近似Hessian矩阵，BFGS逼近逆Hessian矩阵[▽2f(yk+1)]-1的方法为：

(22)

sk=yk+1-yk

(23)

qk=▽f(yk+1)-▽f(yk)

(24)

初始矩阵H0设为对称正定矩阵。BFGS的流程如算法1所示，每次迭代的计算成本为O(m2)，m为决策变量的数量，存储复杂度和计算复杂度与m2成正比例。

算法1基于拟牛顿法的局部开发

Step1初始化：设k=0，选择一个初始点y0，设H0为y0的近似逆Hessian矩阵。

Step2如果不满足结束条件，运行Step 2.1，否则运行Step 3。

Step2.1计算搜索方向：

dk=-Hk▽f(yk)

(25)

Step2.2根据式(21)计算步长αk。

Step2.3计算yk+1=yk+αkdk。

Step2.4使用式(22)-式(24)更新逆Hessian矩阵Hk+1。

Step2.5k=k+1，返回Step 2。

Step3结束迭代程序。

2.3 算法实现

将GSA的主迭代程序描述为一个映射关系：给定一个种群Xt及其速度集Vt，映射为一个新种群Xt+1及其速度集Vt+1，映射公式为：

(Xt+1,Vt+1)=A(Xt,Vt)

(26)

式中：A为映射函数。给定一个点y0，映射为新向量y*：

y*=AqN(y0)

(27)

式中：Aq为粒子q的映射函数。

算法2为采用上述新元素的EGSA算法，算法中Step 2.2如果触发规则，则进行局部搜索。Step 2.3每次迭代结束，运行拟牛顿法。参数tol控制局部开发的强度。

算法2EGSA算法的流程

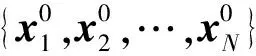
Step2如果不满足结束条件，运行Step 2.1，否则运行Step 3。

Step2.1运行一次GSA迭代：

(Xt,Vt)=A(Xt-1,Vt-1)

(28)

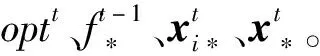
Step2.5t=t+1。

Step3结束迭代程序。

3 基于增强重引力搜索的特征选择算法

3.1 EGSA的解格式

将EGSA的完全解建模为向量格式。设一个矩阵共有n个目标和m个特征，目标是为m个对象和n个特征分配一个类标签。给定一个n+m长度的向量，前n个元素为n个样本的类标签，剩余m个元素为m个特征的类标签。图3是一个解的例子，该例子包括10个样本和8个特征，设样本的分类数k1为3，特征的分类数k2为2。行标签表示为xi∈{1，2，…，k1}，特征标签为yi∈{1，2，…，k2}。

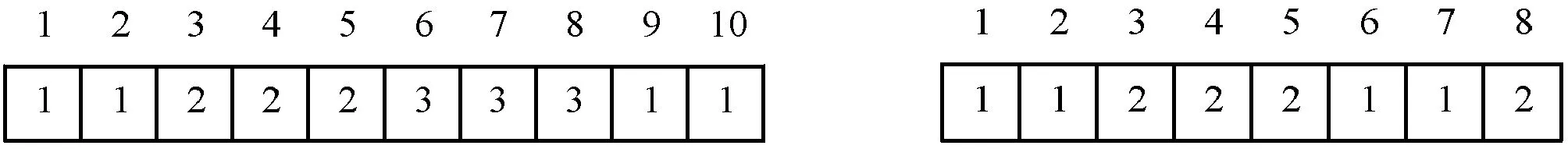
图3 EGSA解的例子

3.2 种群初始化

设计混合初始化方案，一半种群为随机初始化，另一半使用K-means++算法[15]处理，K-means++算法处理数据矩阵获得n行和m列的类标签。图4所示是混合种群初始化的示意图，P为种群总规模，M为每个粒子的列数。

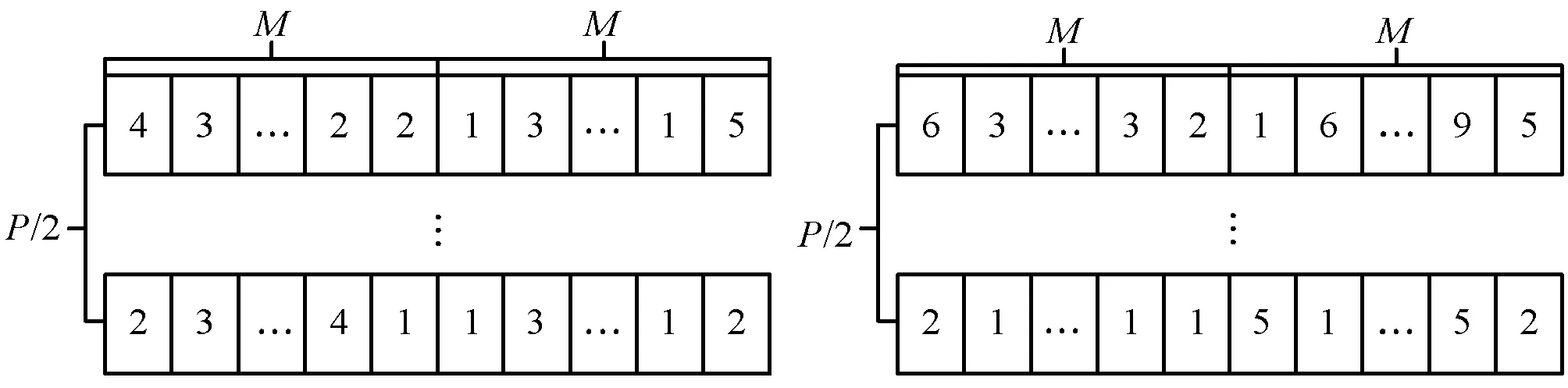
图4 混合种群初始化的示意图

3.3 适应度函数

适应度函数评估解的质量，采用Chi-Sim[13]度量样本和特征间的距离。矩阵R和C为L1范数归一化的相似性值，直接将这些元素转化为不相似值。本文的适应度函数定义为：

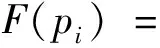
(29)

式中：pi为第i个粒子；δjk为距离的归一化因子。适应度值越高表示解质量越高。第1项对应行聚类，第2项对应列聚类，使用该目标函数计算解的适应度。

3.4 算法流程

图5为协同聚类算法的总体流程图。初始化阶段一半种群为随机初始化，另外一半种群采用K-means++聚类处理。之后每次GSA迭代检查是否满足R1和R2，如果满足则执行局部开发，如果不满足则继续GSA迭代进行全局搜索程序。

图5 算法的总体流程图

4 实 验

4.1 实验数据集

采用6个常用的公开数据集作为实验的benchmark数据集，前2个数据集是UCI的低维小数据集，然后从20Newsgroup语料库选出3个不同复杂度和分类数量的数据集，最终选择典型的高维数据Reuters。表2是6个benchmark数据集的简单介绍，Iris数据集和Wine数据集均具有正定标签，据此评估聚类的结果。20Newsgroup数据集包含约20 000个新闻报道，共有20个分类，每个分类约有1 000个文档，采用该语料库的3个子集：M2、M5、M10，分别包含2、5和10个分类。RT数据集来自于Reuters集合。

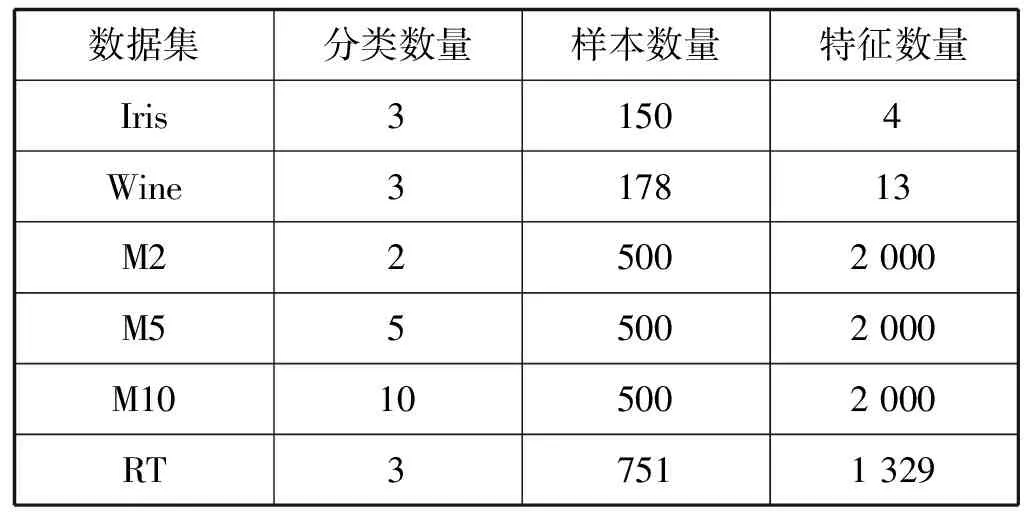
表2 benchmark数据集的属性

4.2 性能评价指标

使用准确率作为性能评价指标，准确率将聚类算法的预测结果和正定值比较来观察算法的准确率。TPi表示分类i的正定值，FPi表示其他类样本被错误分类为i类的样本数量。平均准确率定义如下：

(30)

式中:分母为数据集中样本总数量n。acc值越高表示分类器的准确率越高，每组实验独立运行10次，将10次的平均值作为实验的最终结果。

4.3 参数设置

算法的参数ε=0，γ=1。算法中拟牛顿法局部开发的结束条件设为：

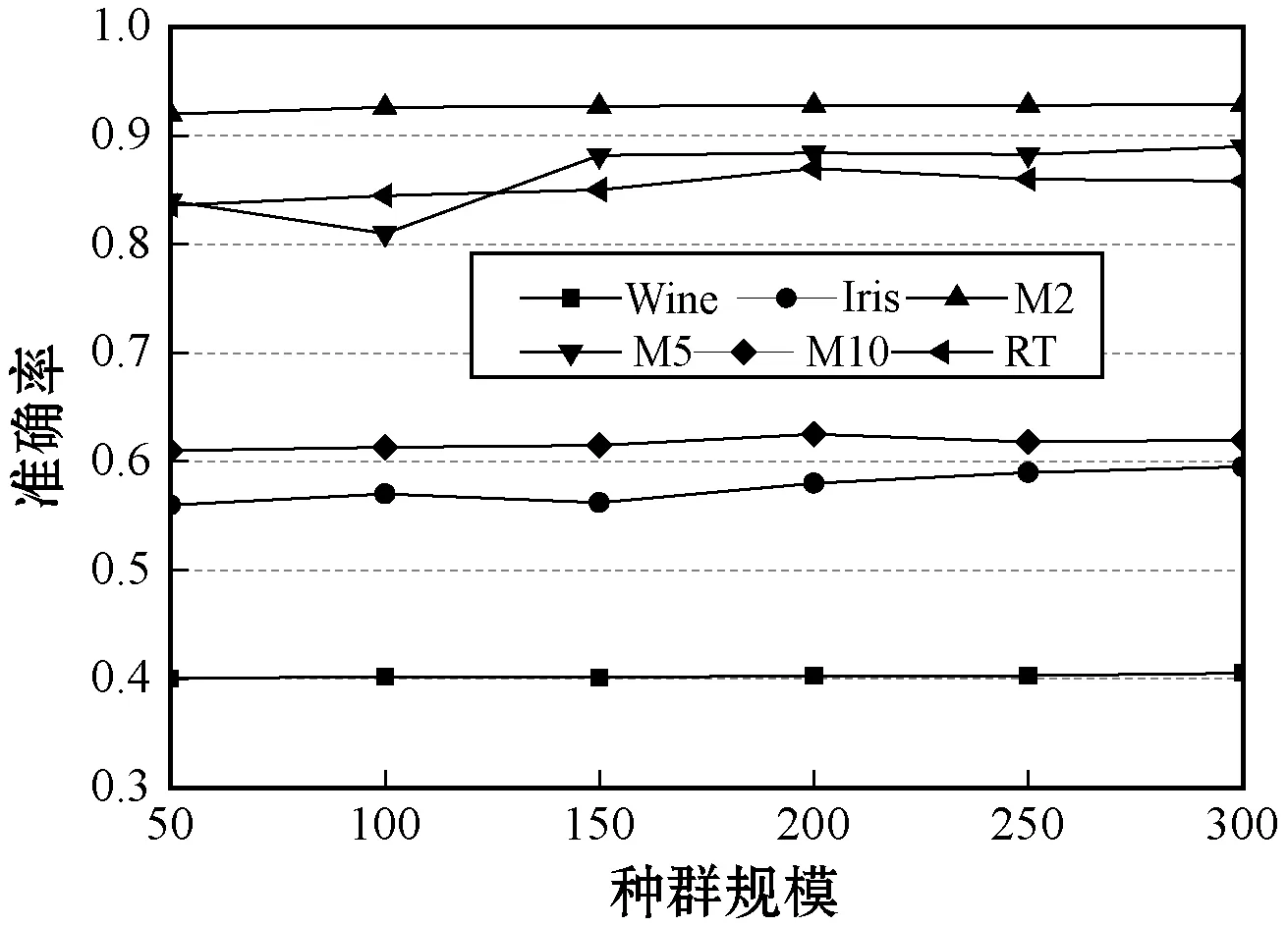
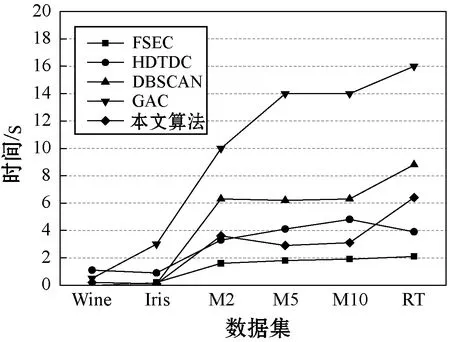
|f(yk+1)-f(yk)|

(31)

式中:tol参数控制局部开发的强度，将tol设为0.01。

(1)迭代次数对于准确率的影响。通过实验评估最大迭代次数对于聚类准确率的影响。将算法的其他参数设为定值：种群规模固定为50，迭代次数从50递增至500。实验结果如图6所示，观察图中结果，对于高维数据集和低维数据集，聚类准确率均随着迭代次数的增加而提高，当迭代次数超过400时，曲线逐渐收敛，因此将最大迭代次数设为400。

图6 迭代次数对于准确率的影响

(2)种群规模对于准确率的影响。通过实验评估重引力搜索算法种群规模对于聚类准确率的影响。将算法的其他参数设为定值：种群规模设为50～300，迭代次数定为400，每组参数独立运行10次。实验结果如图7所示，对于高维数据集和低维数据集，聚类准确率与种群规模的关系较为稳定，为了保持较高的计算效率，实验中将种群规模设为50。

图7 种群规模对于准确率的影响

4.4 局部开发机制的效果

本文算法的一个关键创新是为GSA引入基于逆牛顿法的局部开发机制，因此首先测试本文局部开发机制的效果。选择几个常见的GSA局部开发机制与本文算法对比，分别为基于遗传算法的局部开发机制(简称GSA_GA)[16]、基于混沌置乱的局部开发机制(简称GSA_C)[17]、基于神经网络和模糊系统的局部开发机制(简称GSA_NNF)[18]。

图8为不同GSA对于高维数据集和低维数据集的平均聚类准确率结果。可以看出，GSA_GA、GSA_C、GSA_NNF及本文算法的性能均明显高于原GSA，GSA_GA和GSA_NNF的结果低于GSA_C和本文算法。本文算法采用两条规则选择GSA的优质区域，再通过拟牛顿法对优质区域进行深入开发，实现了较好的总体性能。

图8 不同GSA对于数据集的聚类结果

4.5 与其他聚类算法的比较

本文算法首次将协同过滤技术与GSA算法结合，重点研究本算法对于高维数据集的聚类效果。上文显示本文的重引力搜索算法有效地增强了原重引力搜素算法的性能，此处将本文算法与其他聚类算法比较，评估本文算法的总体性能。对比方法分别为经典的DBSCAN[19]、GA聚类算法[20]，以及两个高维数据的聚类算法。FSEC[21]是一种基于特征优化分组的集成式高维大数据聚类算法，该算法也利用协同聚类的思想，并且构建集成式聚类算法的框架，对高维大数据实现理想的聚类结果。HDTDC是一种基于改进布谷鸟搜索的和语义索引的高维数据聚类算法，该算法也利用协同聚类算法的思想，并且首次利用布谷鸟搜索算法对高维文档数据集进行聚类处理。

图9为5个聚类算法对于6个数据集的聚类准确率结果。可以看出，FSEC对于Wine和Iris数据集的准确率较低，远低于其他4种算法，而FSEC对于M2、M5、M10和RT 4个高维数据集的准确率较高。DBSCAN则对Wine和Iris数据集的准确率较为理想，但对于M2、M5、M10和RT 4个高维数据集的准确率处于明显的劣势。FSEC和HDTDC两个近期的算法实现较为理想的聚类准确率，并且具有良好的稳定性。本文算法对于6个不同数据集均实现最佳的聚类结果，对于高维数据集的性能优势更加明显。

4.6 算法的时间效率

高维数据中包含大量的噪声信息和冗余信息，给算法的处理时间带来了极大的挑战。图10为5种算法对于6个不同数据集的平均聚类处理时间。可以看出，FSEC将特征优化分组，采用并行处理框架获得了最低的计算时间。GAC的种群规模较大，每次迭代包含交叉算子、变异算子和选择算子的处理，算法的计算时间较长。DBSCAN对于低维数据集的处理速度较快，但对于M2、M5、M10和RT 4个高维数据集的速度较慢。本文算法对于高维小样本数据集的处理效率较为理想，但对于高维大样本数据集的效率较为一般。

图10 5种算法对于6个不同数据集的平均聚类处理时间

5 结 语

本文设计协同相似性矩阵度量数据集的样本相似性和特征相似性，以二部图形式建模特征和数据点的关系；设计拟牛顿法的局部开发策略，提高重引力搜索的求解质量。基于高维数据集和低维数据集进行仿真实验，结果表明，本文算法对于不同维度的数据集均实现理想的聚类准确率，并且对高维小样本数据实现较高的计算效率。但本文算法对于高维大样本数据的时间效率较为一般，未来将专注于本文算法应用于高维大样本数据集的研究，在提高聚类准确率的前提下，保持较快的处理速度。