基于深度神经网络的多模态特征自适应聚类方法
2020-10-15敬明旻
敬 明 旻
(中国石化石油工程技术研究院信息与标准化研究所 北京 100101) (中国社会科学院数量经济与技术经济研究所 北京 100732)
0 引 言
深度神经网络对各种单模态数据表现出极强的特征学习能力,目前已在许多领域内均取得了令人瞩目的成果,包括视频识别[1]、语音识别[2]和心电图识别[3]等。在实际应用中存在大量多模态特征的数据,例如:多媒体的音频数据和视频数据,医学领域的多个生物信号监测数据等。这些数据不同模态的特征之间存在相关性,将多模态特征融合,能够有效地提高总体的分类效果。虽然自编码器、卷积神经网络、对抗网络等深度神经网络在单模态特征学习方面表现出较强的能力,但是将多个模态的特征融合是深度神经网络的一个难点。
文献[4]将新闻文字和视频特征融合,以文字内容为支配特征,以语音特征和视频特征为辅助特征,在提取相同底层特征的情况下,该分类算法实现了性能提升。文献[5]根据人脸和姓名的共现关系,分析文本姓名位置对姓名重要程度的贡献,使用反向传播神经网络融合上述信息,实现了较高的新闻人脸识别率,对于噪声也具有鲁棒性。除了新闻领域,生物应用中不同生物信号之间也存在极大的相关性,因此多模态特征融合技术在生物领域也具有广阔的应用前景。文献[6]将人脸、指纹等多个生物特征融合,用以提高身份验证的安全性。近期研究人员将多特征融合引入推荐系统,也成功提高了推荐系统的性能[7-8]。
多特征融合技术的最大优势是在仅提取底层特征的情况下,即可有效地提升分类算法的性能[9]。深度神经网络广泛应用于模式识别领域,而深度神经网络的超参数繁多,且对不同数据所提取的特征形式也存在差异,导致将深度神经网络学习的多模态特征集融合成为一个难题。为了解决上述问题,本文提出兼容不同深度神经网络模型的多模态特征融合方案。
1 方法设计
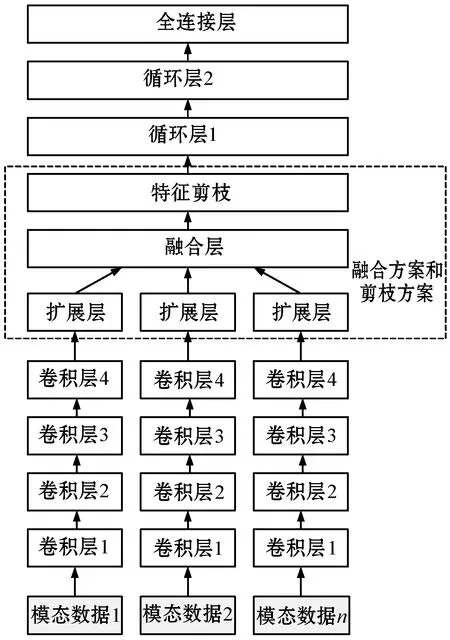
本文方法主要由扩展层和融合层两部分构成,如图1所示。
1.1 扩展层
不同网络的输出向量输入扩展层,神经网络可以是任意类型的深度学习网络。不同模态的特征格式不同,特征向量大小也可能不同,因此在扩展层首先将特征向量转化为相同长度。
假设共有m个模态网络,设x(k)为第k个网络的输出向量,其中k∈{1,2,…,m}。第k个扩展层输入向量为:
z(k)=w(k)·x(k)+b(k)
(1)

(2)
d(k)=[d1(k),d2(k),…,dc(k)]T,扩展层输出向量的维度均为c,即i∈{1,2,…,c}。
1.2 融合层
融合层收到扩展层的m个向量,每个向量的元素数量为c。融合层将这些向量重组成一个长度为c的向量,称为融合向量。采用多项式采样技术融合多个模态的向量,设多项式采样的向量为ri=[ri(1),ri(2),…,ri(m)]T,使其满足以下的多项式分布:
ri~Mn(1,p)
(3)
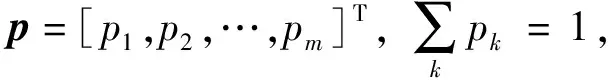
(4)
式中:“∘ ”表示Hadamard积。最终,融合层输出向量e=[e1,e2,…,ec]T的第i个元素表示为:
(5)
e的长度和d(k)的长度相等,将输出结果输入终端网络,终端网络的输出则是分类问题的最终决策。
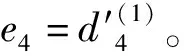
1.3 模态间的相关性分析
在扩展层考虑了模态特征间的相关性。每个模态的扩展层独立产生d(k),然后筛选出一部分向量输出到融合层。每次训练中多项式采样技术随机采样每个模态的特征,因此对于相同的输入数据,融合的特征向量应该相似。该机制保证模态的扩展层既学习了本模态的数据,也学习了其他模态的特征。
1.4 处理缺失的数据
在实际应用中可能发生一部分模态数据缺失的情况,例如:某个无线传感器可能断开连接,导致一段时间内该模态数据缺失。融合层通过调节概率p能够实现对缺失数据的鲁棒性。设u=[u1,u2,…,um]T为一个二值向量,表示对应模态数据是否存在:
(6)

(7)
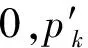
1.5 正则化分析
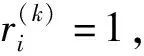
(8)
式中:Bi表示二项式分布;pk为传到下一层的成功率。
随机变量的二项分布等价于贝努利分布,因此这个过程等价于对神经网络的随机失活(dropout)[10]处理,输出向量每个值的失活概率为(1-pk),基于失活的正则化处理可防止过拟合。虽然结合层的设计初衷是选择合适的模态进行融合,但也能够防止训练阶段的学习过程出现过拟合的情况。
2 多神经网络的剪枝方法
通过剪枝冗余的特征减少最终深度神经网络模型的特征量,缩小网络规模。
2.1 卷积特征聚类和剪枝

(9)

2.2 冗余滤波器剪枝
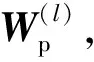
算法1冗余卷积特征的剪枝算法
1.FOREACH层lIN训练模型DO
2.读取W(l)的卷积特征;
3.调节参数τ;
4.(Lf,nf)=representation_feature(W(l),τ);
//提取代表滤波
5.k=0;
6.FORiINLfDO
7.W(l)的第i列拷贝到W′(l)中;
//初始化剪枝的模型
8.k++;
9.ENDFOR
10.初始化W′(l)的权重;
11.微调剪枝的网络模型;
算法2representation_feature函数
输入:W,τ。
输出:Lf,nf。
1.遍历W的向量,将相似性大于τ的向量分类。
2.从每个分类中随机采样一个代表特征。
3.返回代表特征的序号列表Lf和分类数量nf。
图2为描述剪枝处理和不剪枝处理差异的示意图。原网络共有5个滤波,每个滤波对应核矩阵W(l)的一列。滤波和三维输入图像Zl卷积获得5个特征图Zl+1。通过核矩阵W(l+1)将特征图Zl+1连接到l+2层,设W(l)的列分成3类{1,3,5}、{2}、{4},滤波1、3、5之间的相似性大于τ。调用算法2获得的索引列表为{1,2,4},nf=3,滤波3和滤波4标注为冗余滤波。剪枝处理在Zl+1中将滤波3和滤波4及其他对应的特征图剪枝,同时删除下一个卷积层的特征图权重。
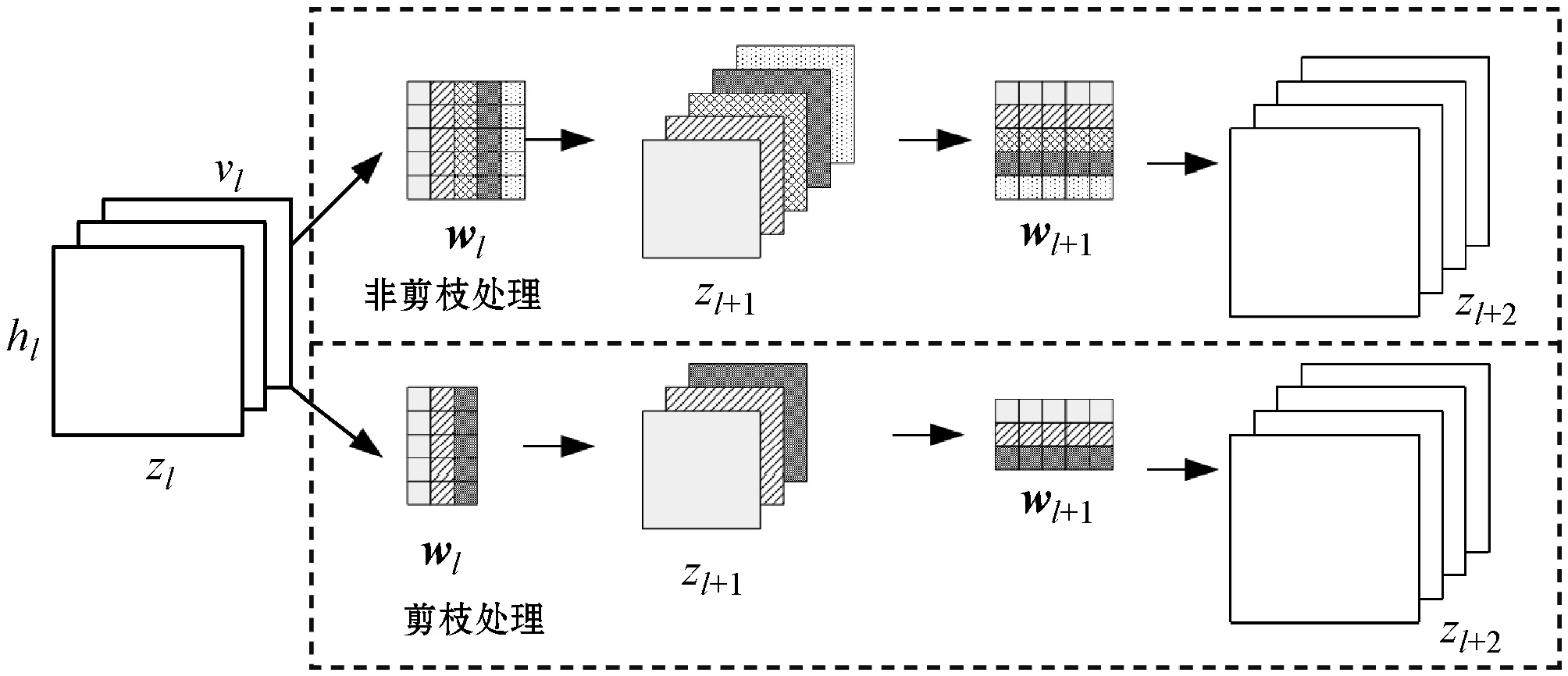
图2 剪枝处理和不剪枝处理的差异图
3 多模态特征融合的超参数学习
深度神经网络包含随机失活处理和修正线性单元处理导致模型非线性且不平滑,所以一般采用群体智能和模拟退火等算法对网络超参数进行优化,但这些算法的寻优质量不佳。本文设计一种动态编码搜索算法的深度神经网络超参数高效率优化算法。
3.1 深度神经网络的超参数优化问题
将深度神经网络超参数优化视为一个黑盒误差函数f的全局优化问题,优化f的问题定义为:
(10)
式中:Ztrain和Zval分别表示训练数据集和测试数据集;θ为学习参数,通过最小化训练误差来学习θ;x为一个超参数集。
深度神经网络结构相关的超参数包括学习率、损失函数、最小批大小、迭代次数和动量。神经元相关的超参数决定了每层的大小和非线性变换的方式,具体包括隐层单元数量、权重衰减、激活稀疏性、非线性、权重初始化、随机种子和预处理输入数据方式等。
3.2 动态编码搜索算法(Dynamic Encoding Searching,DES)
DES[11]能够快速地搜索成本函数的全局最优值,分为局部搜索和全局搜索两个阶段。局部搜索负责开发局部区域,包括二分查找(Binary Search,BS)和单向搜索(Unidirectional Search,US)两个步骤。全局搜索负责搜索全局的最优区域,采用多起点方法实现。
(1)局部搜索阶段。DES局部搜索阶段包括BS和US两个步骤,BS在任意二进制数的最低有效位(Least Significant Bit,LSB)右侧增加0或1,使对应的实数值分别减小或增大。

(11)
式中:bi∈{0,1},i=1,2,…,m。解码函数存在以下关系:
(12)
如果sp全为0,那么左侧相等;如果sp全为1,那么右侧相等。超参数优化程序采用以下的无偏二进制解码函数:
(13)

BS函数处理x1之后,沿着最优方向dopt重复运行US函数,直至解的质量不再提高。如果dopt为0,则产生相邻数值s′=s*-1;如果dopt为1,则s′=s*+1。US函数程序获得最优的行s*,将s*保存于最优矩阵D*的第一行。然后BS开始x2方向的局部搜索,最终完成对所有行的搜索,最优矩阵D*变为一个矩形矩阵。
算法3局部搜索算法
//解码初始化矩阵
2.FOREACHi=1TOnDO
3. BS(B*);
//二分查找
4. US(B*);
//单向编码搜索
5.ENDFOR
/*BS(B*)函数*/
6.r1×k=B*(i,1:k);
//读取当前最优矩阵的第i行
7.FOREACHj=0TO1DO
8.θj←θ*;
//读取当且最优的参数向量
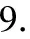
//第i行向量加一个二进制比特j;

//更新解码的参数;
11.Jj=f(θj);
//评估新参数向量的成本;
12.ENDFOR
13.J*=min(J0,J1);
//选择更小的成本函数;
14.IFJ*==J0THEN
15.dopt=0,s*=s0,θ*=θ0;
16.ELSE
17.dopt=1,s*=s1,θ*=θ1;
18.ENDIF
/*US(B*)函数*/
19.WHILE不满足迭代结束调节DO
20.θ′←θ*;
21.IFdopt==0THEN
22.s′=s*-1;
23.ELSE
24.s′=s*+1;
25.ENDIF
26. 采用第i个参数更新参数向量;
27.θ′(i)=fd(s′);
28.J=f(θ′);
//评估新参数向量的成本;
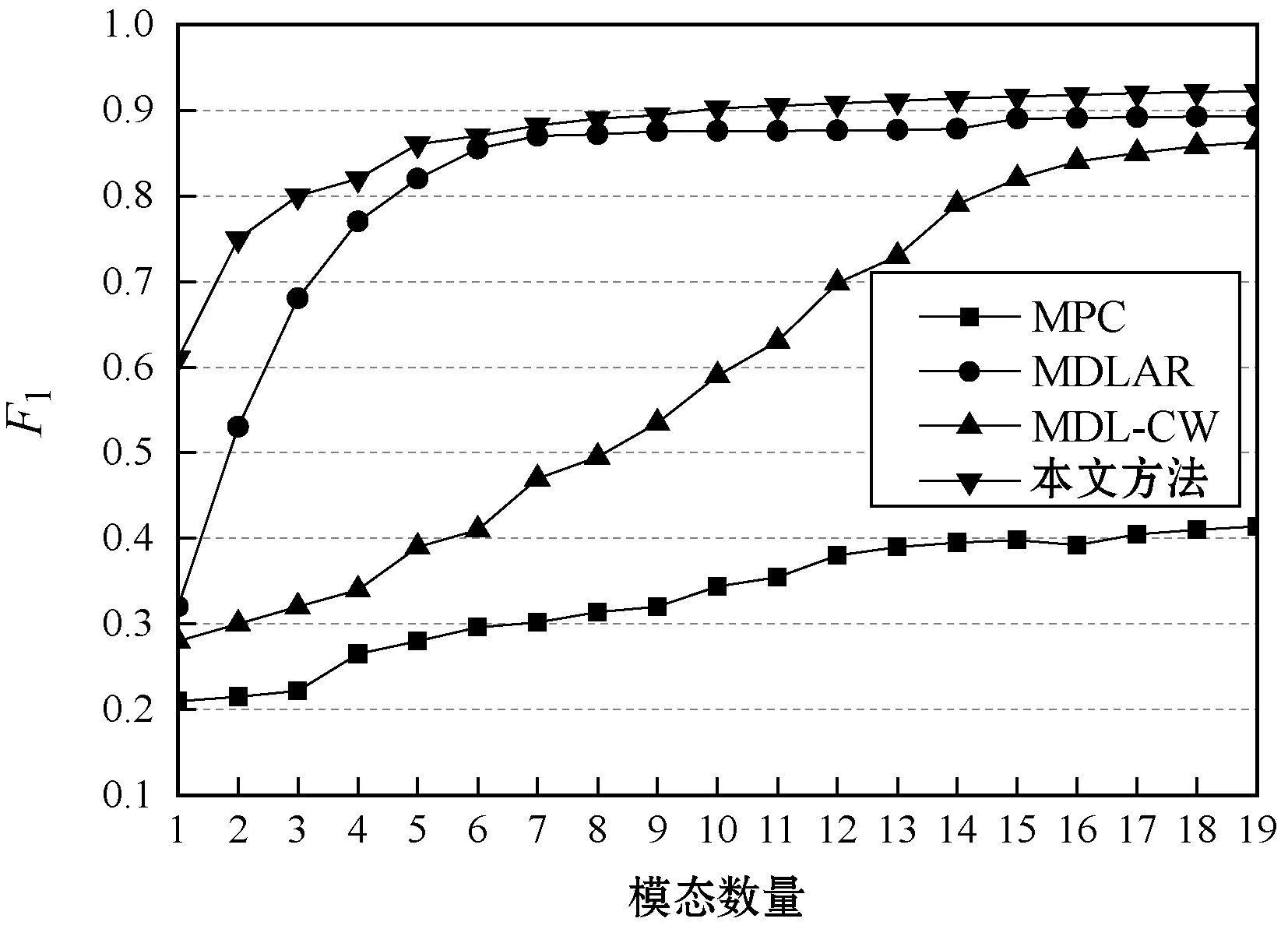
29.IFJ 30.s*←s′,J*←J; 31.ELSE 32.RETURN; 33.ENDIF 34.ENDWHILE (2)基于多起点的全局搜索阶段。搜索空间分为连续逐渐缩小的网格,根据成本函数的形状自动决定搜索路径。因为不同初始化矩阵的搜索路径可能在一个子矩阵出现重复,导致重复计算,为此创建一个查找表,为二进制矩阵在表中产生一条记录,通过比较记录来避免重复搜索。DES通过检查LENTH_T和COST_T两个参数跳出局部最小。如果当前最优矩阵的行长度等于LENTH_T,且成本大于COST_T,则停止搜索,随机选择一个新起点重新搜索。本文将LENTH_T设为矩阵最小的行长度,COST_T设为局部最优和局部次优值的中位数。 (3)基于DES的超参数优化方法。图3为超参数优化方法的流程图。第一步,预处理步骤确定并初始化神经网络的超参数,例如:批大小、epochs数量、学习率等。该步骤也需要确定深度神经网络的类型,包括卷积神经网络、递归神经网络、对抗神经网络、自编码器等。第二步,使用初始化值训练超参数,更新DES的成本函数。第三步,采用更新的成本函数再次运行DES获得新的超参数,采用新的超参数重新初始化和训练神经网络,经过DES的若干次迭代处理,获得最小化网络成本的最优超参数。 图3 DES优化超参数的流程框图 实验环境为CPU Intel Core i7-6700,主频为3.4 GHz,内存为64 GB,操作系统为64位Ubuntu 14.04。采用经典的MNIST数据集单独测试本方案每个机制的有效性,数据集包含60 000幅训练图像和10 000幅测试图像,图像大小均为28×28像素。 (a)1个隐层的实验 为了评估本文超参数优化机制DES的效果,将其与模拟退火[13]、遗传算法[14]、粒子群优化算法[15]等经典优化方法比较。采用图5(a)所示的卷积神经网络模型,将分类精度的倒数作为成本函数。图5(b)是4个优化算法的收敛曲线,模拟退火算法在第8次迭代的成本为1.011 43,遗传算法在第23次迭代的最小成本为1.012 65,粒子群算法在第233次迭代的最小成本为1.011 071,本文算法在第263次搜索的最小成本值为1.008 98。本文算法实现最低的最小成本,卷积层神经元数量为64,全连接层的神经元数量为512,学习率为10-3,p=0.5。 (a)卷积神经网络的结构 将MNIST的每个图像剪裁为左右两半,图6是两个模态的卷积神经网络结构,采用4.3节的超参数,图中输入是数字“4”剪裁为左右两半的实例。设置两个卷积层,直接集成法直接聚合全连接层的结果,传递至Softmax层。本文融合方法对两个全连接层的结果进行融合,再传递至Softmax层。 (a)融合方案 (b)直接集成 使用60 000个双模态样本训练网络模型,测试了10 000个测试样本的分类错误率,分别测试了完整图像、左半边图像缺失和右半边图像缺失的情况,缺失的半边图像替换为全零的数据。表1为实验结果,可看出本文融合方法在完整图像的情况下实现微小的提高,在缺失半边图像的情况下则实现了大幅度的提高。 表1 MNIST数据集的平均分类错误率 % (1)实验数据集。OPPORTUNITY[16]是一个多个模态的动作识别数据集,数据集由5个自由动作序列和1个受限动作序列组成,所有数据的采样频率为30 Hz。本文构建运动模式识别和手势识别两组实验,运动模式分为4个类,即站立、行走、坐和躺,手势分为17个类,即开洗碗机、关洗碗机、开吹风机1、开吹风机2、开吹风机3、关吹风机1、关吹风机2、关吹风机3、开冰箱、关冰箱、开门1、开门2、关门1、关门2、移动杯子、清洁桌子、其他。 人物1和人物2的数据集作为训练数据集,人物3的数据集作为测试数据集。将所有的采样数据归一化到[-1,1]。滑动窗口设为500 ms,测试数据的步长设为250 ms,训练数据的步长设为33.3 ms。 (2)性能评价指标。采用F1评价分类的性能,定义为: (14) 式中:ni为第i个类的数据量;n为总数据量;prei为第i个类的准确率;reci为第i个类的召回率。(ni/n)项能够平衡偏态分布的分类。 (3)对比算法。目前深度神经网络多模态融合技术依然较少,选择3个优质的多模态技术与本文方法作比较。MPC[17]是一种专门为卷积神经网络设计的多模态分类算法,该算法主要对池化层进行线性融合,但无法扩展到其他的神经网络模型。MDLAR[18]是一种专门为动作识别设计的多模态受限玻尔兹曼机模型,该模型对动作识别的性能较好。MDL-CW[19]是一种基于权值的跨模态深度神经网络融合算法,通过多个阶段的预训练迭代调节每个模态的权值。其中两个方案都提供了卷积神经网络的实现方案,因此将本文方法和卷积神经网络集成。 (4)网络模型。本文多模态卷积神经网络的网络结构如图7所示。 图7 本文方法和卷积神经网络的集成结构 (5)实验结果和分析。图8为4个多模态神经网络的实验结果。MPC主要对池化层进行线性融合,对多模态之间的非线性拟合能力不足,因此其总体分类性能较低。MDL-CW是一种基于权值的跨模态深度神经网络融合算法,通过多个阶段的预训练迭代调节每个模态的权值,基于权值融合的方法在特征量少的情况下难以实现理想的学习效果,而在特征量大的情况下容易出现过拟合,其总体分类性能也较低。MDLAR和本文方法的性能明显好于另外两个算法,MDLAR通过对多模态玻尔兹曼机的非线性融合,对多模态特征的学习能力较强,并且该模型对动作识别问题制定了专门的超参数学习机制,实现理想的性能。本文方法通过多模态特征融合和特征剪枝处理,不仅有效地实现了非线性特征学习,而且也避免过拟合问题,最终实现了最佳的分类性能。 (a)运动模式分类实验 为了解决深度神经网络的多模态特征融合和分类问题,本文设计基于深度神经网络的多模态特征自适应聚类方法。该方法能够兼容不同的深度学习网络,分别与多层感知机和卷积神经网络进行集成实验,实现稳定的性能。本文方法考虑跨模式的特征相关性,学习程序通过正则化处理防止过拟合,对于数据缺失也具有鲁棒性。 因为本文方法需要将多个深度神经网络融合,因此超参数的学习是一个难题,本文设计的动态编码搜索策略能够提高神经网络的优化效果,但对于大量的模态融合问题,还存在计算时间过长的问题。未来将关注于对多个神经网络的超参数进行联合优化,以期提高模型的学习效率。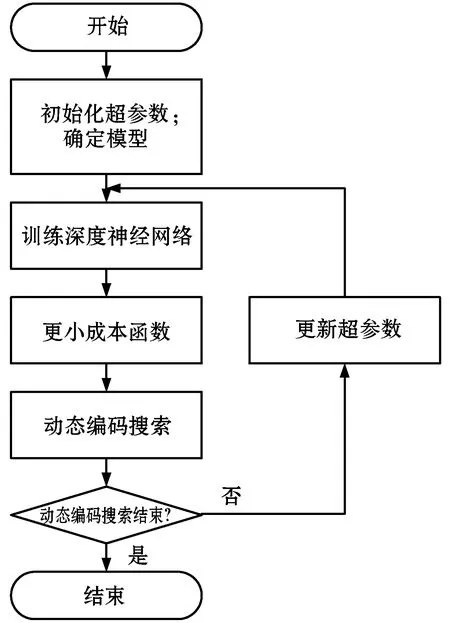
4 仿真实验
4.1 实验数据集和实验环境
4.2 特征剪枝实验

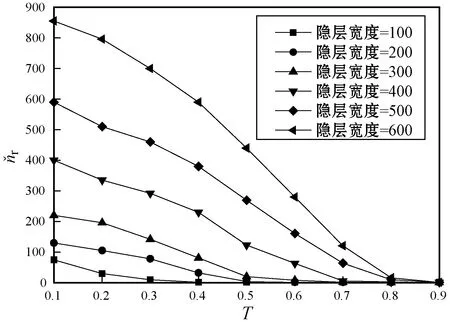
4.3 DES的超参数优化实验
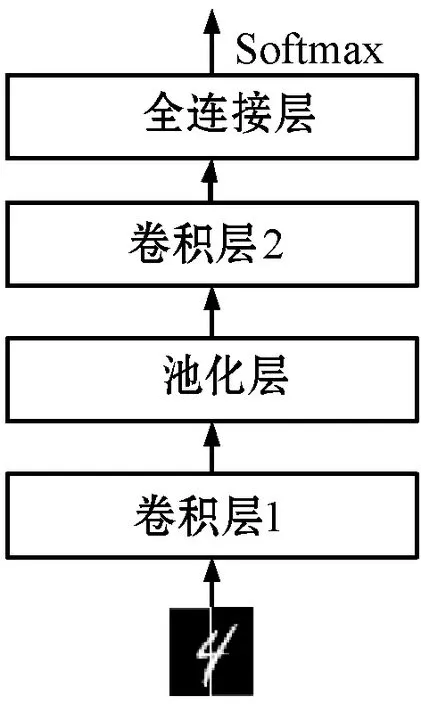
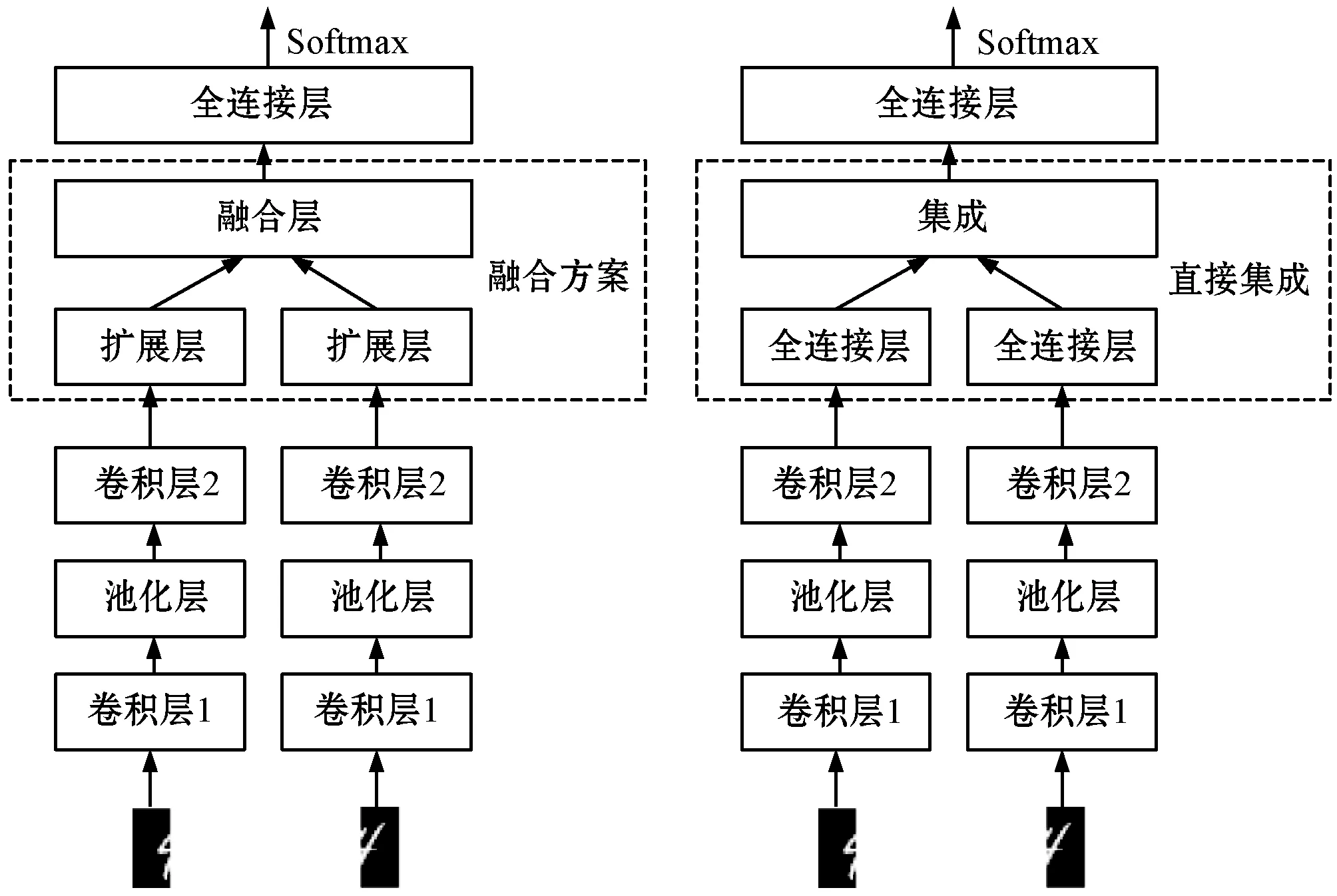
4.4 两个模态的融合实验
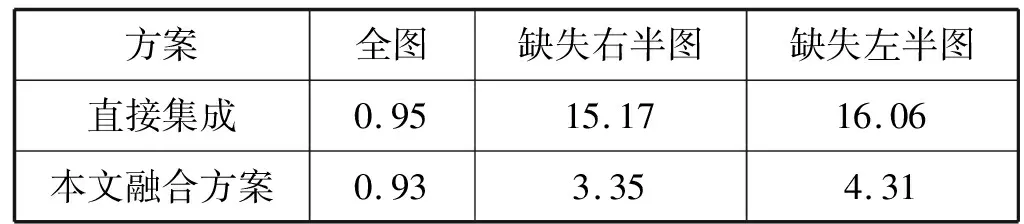
4.5 对比实验分析
5 结 语
