基于信息熵的多尺度FAST角点

陈 磊 韩 飞 易文祥

(广东工业大学机电工程学院 广东 广州 510006)

0 引 言

特征点提取是图像匹配、识别以及目标跟踪等诸多计算机图像应用的预处理步骤，而图像角点是非常有效和稳定的一种特征点策略[1]。图像角点往往是图像边缘交叉点，局部的梯度剧烈变化点。目前图像角点检测算法有Harris角点[2-3]、SUSAN角点[3-4]、FAST角点[5]。FAST角点精确度高、角点质量稳定，它基于图像灰度值操作、算法效率高、计算简单，相比其他特征点。其计算效率更加突出。但基本的FAST角点不具备尺度不变性，而基于FAST角点改进而来的ORB算法[6]和BRISK算法[7]以及Harris-Laplace算法[8]等均是先构建多尺度金字塔，然后在尺度空间检测角点，最后对所有检测到的角点进行筛选，以得到尺度不变的特征点[9]。这样的多尺度分析流程过于冗长且计算复杂，大大降低了算法的实时性。在基于图像边缘曲率信息的检测方法中，李伟生等[10]提出一种基于曲率多尺度的自适应角点检测方法，利用曲率多项式和构造局部曲率显著度，增强了角点对图像尺度、旋转变化的鲁棒性。而结合信息熵的图像预处理算法研究也是热点研究方向，如：周保余等[11]提出基于信息熵的多尺度描述子改进，通过计算高斯差分空间内多层SIFT描述子，同时统计每层特征点的局部信息熵，根据各层信息熵的总占比进行加权求和以得到最终结合了多个尺度层的描述子；蔡青等[12]提出一种基于信息熵的自适应尺度活动轮廓图像分割模型，利用图像信息熵构造自适应尺度算子，使模型能根据图像灰度不均匀的程度自动调节尺度，提高模型对灰度不均匀图像的分割速度；高飞[13]等提出一种基于分块信息熵和特征尺度的图像配准算法，通过对图像进行分块，结合每块图像的信息熵，改善了Harris-Laplace算子提取特征点分布过于集中的问题。

本文根据图像信息熵与尺度变化的联系，提出并拟合了尺度信息熵模型，该模型基于高斯尺度空间，主要通过信息熵进行图像的相对尺度参数求解。基本的FAST角点受限于其固定的作用域，不能很好地适应图像的尺度变化，因此本文提出基于尺度信息熵模型的自适应作用域的FAST角点，以变化的角点算子作用域提高尺度适应性。

1 FAST角点

FAST算法对每个像素点周围离散化的Bresenham圆上的灰度值与该点进行阈值比较，以判定是否为角点。最基本的FAST角点是检测以3个像素为半径的圆周上的16个像素点，如图1所示，如果连续n个点的灰度值都比中心点大或者小的话，则该点就是角点，实际上计算中需要加上阈值t。根据不同的n，FAST角点又可以写为FAST-n，常见的有FAST-9、FAST-10、FAST-11、FAST-12。

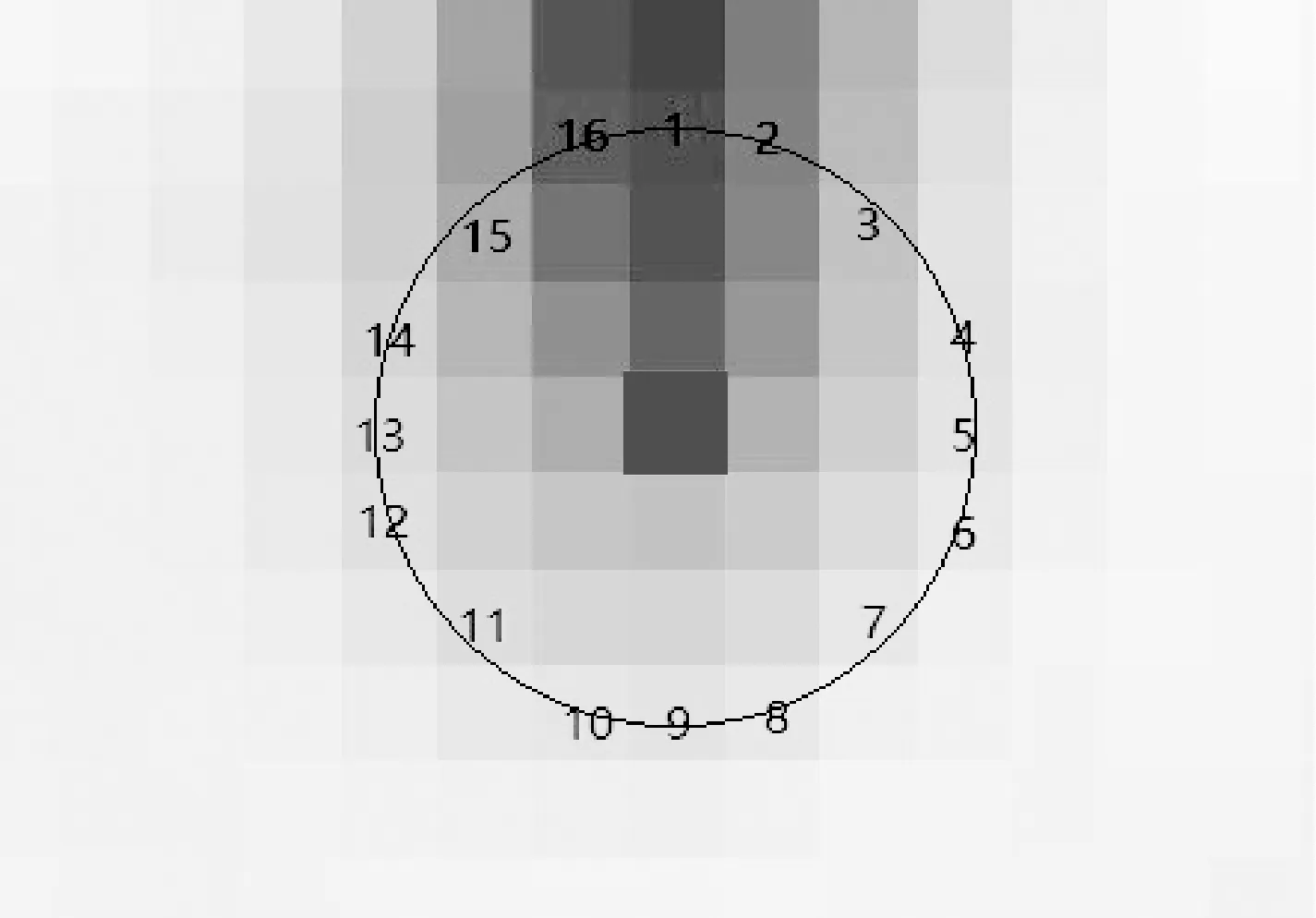
图1 FAST角点示意图

FAST角点的最大优势就是其计算效率，但由于其固定的作用域导致其不具备尺度适应性，目前的FAST角点的多尺度分析方法是在高斯金字塔的各个尺度层分别提取FAST角点，最后累计所有尺度层的兴趣点进行响应值抑制。FAST角点也作为很多局部特征算法的特征点并加以改进，例如ORB算法、BRISK算法和FREAK算法均是在FAST角点的基础上进行多尺度改进提取特征点。

2 尺度信息熵模型

2.1 信息熵

香农(Shannon)为了解决信息的度量问题在1948年提出了信息熵，图像信息熵反映了图像平均信息量的大小。

对一幅图像f(x,y)，其信息熵为：

(1)

式中：k为灰度级数目；pi表示灰度为i的像素值出现的概率。

根据Shannon定理，当图像灰度越均匀，各灰度值概率趋近于相等时，图像的信息熵越大。当图像尺度发生变化时，高尺度图像灰度较平滑，即其相邻灰度值差异就会很小，因此图像梯度值就趋近于相等，其梯度图像就能反映图像平均信息量。对于计算信息熵，梯度图像的各点幅值相对更小，其全局的信息熵结果变化范围更集中，更容易实现数据的归一化。因此本文并不直接对灰度图像计算信息熵，而是以梯度图像研究图像尺度变化与信息熵的关系，具体实现以一阶前向差分进行计算。

2.2 模型建立

本文实验以高斯模糊G(x,y,σ)模拟图像的尺度变化建立尺度空间，由于高斯函数在原点的3σ半径范围内包含了99%的信息，所以具体的高斯模糊系数由式(2)决定，以递增的高斯滤波器尺寸ω表示不断增大的尺度系数σ：

ω=3σ×2+1

(2)

根据式(2)确定尺度系数，具体滤波器尺寸与尺度系数取值如表1所示。

表1 高斯滤波器尺寸与尺度系数关系

本文实验是在生活环境下采集实验图像，图2为实验中采集的部分图像。

图2 部分实验图像

根据表1的参数关系，对每幅图像进行10个尺度系数的高斯模糊构建尺度空间，然后计算每个尺度层的梯度图像和全局信息熵。图3为图2中显示的部分图像的尺度空间与对应的梯度图像全局信息熵变化关系。

图3 图2中图像的高斯滤波器尺寸与梯度图像信息熵的变化关系图

可以看出，实验图像在尺度变化下其梯度信息熵与高斯滤波器大小的变化出现了相同的趋势。依据Shannon定理，在图像发生尺度变化的过程中，尺度系数越小越靠近低尺度的图像，其灰度离散程度越明显，局部相邻的灰度差异越大，其梯度图像的像素值也就越离散，此时的梯度图像信息熵变化就越显著；而当尺度系数不断增大，滤波器的平滑面积越大，高斯滤波后的图像灰度值就越趋近于平均值，其梯度图像各点像素值也就越相似，形成的平滑效果就越微弱，所以其梯度图像信息熵变化趋势就越平坦。

2.3 模型拟合

对尺度系数与信息熵的变化关系进行模型拟合以得到尺度信息熵模型的数学函数表达式。经过多次实验，本文最终以幂函数进行模型拟合，其函数类型为：

H=k1ωk2+k3

(3)

式中：k1、k2、k3为三个系数。图4为部分拟合实验中系数分布情况。

图4 幂函数拟合的系数分布情况

可以看出，幂函数拟合尺度信息熵模型的三个系数值浮动情况不一致，k1的离散程度较大，主要分布在-1到-3之间，k2主要分布在0到-1.5之间，而k3拟合值相对集中，主要以1为中间值小幅波动。因此，为保证模型的泛化能力，对k1、k2的取值以区间表示，实际应用时可以根据经验取值，本文则根据实验数据以平均值进行后续计算，其中k3取值为1，k1和k2取值结果如表2所示。

表2 幂函数拟合模型的系数取值

因此本文使用幂函数拟合的尺度信息熵模型表达式为：

H=-1.9ω-0.84+1

(4)

根据式(2)，有信息熵与尺度系数的模型为：

H=-1.9(6σ+1)-0.84+1

(5)

根据单幅图像的拟合数据进行分析得知，如果图像内容有较多的噪点区域，则该图像的模型拟合效果就会较差，其模型系数会出现较大的波动甚至超出最优的取值区间。在得到确定的尺度信息熵模型表达式后，对发生尺度变化的高尺度图像计算其梯度图像的全局信息熵H，根据式(4)和式(5)便可分别求得该高尺度图像对应的高斯模糊滤波器大小和尺度系数。因为本文的尺度信息熵模型是基于模拟的高斯尺度空间拟合得来，所以解得的尺度系数和高斯滤波器大小都是相对于该图像对应的理论上的低尺度图像而言的。实际中的图像会存在噪声等因素的干扰，解得的信息熵会较低，所以实际计算当中需要对图像的梯度信息熵进行一定比例的放大再计算相对尺度参数。

3 多尺度FAST角点

图像发生尺度变化其实就是高斯平滑，发生尺度变化的图像，局部范围内的灰度值会更加平滑，邻域内的像素点差异程度减弱，随着尺度系数的增加，平滑区域逐渐增大。基本FAST角点不具备尺度不变性，究其原因，FAST角点是以半径为3像素的圆周上检查16个点与中心点的灰度差异进行判断，固定的角点算子作用域在图像发生尺度变化后，不能有效地提取灰度差异性。尺度变化下FAST角点算子作用域如图5所示。

图5 尺度变化下FAST角点算子作用域

尺度变化后，FAST角点算子已经不能适应局部特征的灰度差异，边缘区域的灰度变得平均，且亮区和暗区过渡缓慢同时过渡区域变大，FAST角点的固定圆周很难覆盖满足阈值条件的灰度区域，因此扩大其圆周，增大算子作用域是一个有效的解决方法。本文根据前面的研究提出基于尺度信息熵的自适应作用域的FAST角点算子以适应不同尺度的图像。

自适应作用域即计算图像的信息熵并通过式(4)得出高斯滤波器尺寸ω，然后以此ω作为FAST角点检测作用域的圆周半径。半径为ω的作用域同样根据bresenham算法确定的离散圆，不同半径大小的bresenham圆周上分布的像素点数量和位置均不一样，具体程序实现时，可以根据不同半径的bresenham圆建立查询表方便计算。

图6展示了半径为3、4、5的bresenham圆以及圆周上的像素点位置。表3为不同半径的bresenham圆周上对应的像素点数量。

图6 不同半径的bresenham圆周

表3 不同半径的bresenham圆对应像素点数

本文基于尺度信息熵模型的自适应作用域FAST角点的检测流程如图7所示。

图7 基于尺度信息熵模型的多尺度FAST角点计算流程

4 实验与结果分析

为了验证本文多尺度FAST角点的尺度适应性，与基本的FAST角点、多尺度的Harris-Laplace角点和BRISK特征点进行角点检测对比实验。实验在发生尺度变化的图像集上进行角点检测，4幅图像的尺度连续增大，对不同算法的检测效果进行对比。由于FAST角点检测效果依赖于阈值的大小，随着图像尺度的增大，为了保证显示效果，对FAST角点和本文算法的阈值进行降低，实验中3种角点算法检测中4幅图像的阈值设置为50、40、30、20。根据基于尺度信息熵模型的多尺度FAST角点算法流程进行计算，本文算法应用到4幅图像上的FAST角点作用域半径分别为4、6、6、7，实验中的FAST角点的非极大值抑制范围也是根据作用域大小决定的。本文实验环境为Intel Core i5和MATLAB 2016b。

图8-图11分别为基本FAST角点、Harris-Laplace特征点、BRISK特征点和本文多尺度FAST角点的检测效果。图12为该图像集在不同算法检测的角点数量统计。图中白色点为角点，图9和图10中白色圆环则为Harris-Laplace算法和BRISK算法中尺度金字塔检测到的特征尺度大小。基本FAST角点随着图像尺度增大，检测到的有效角点急剧减少，BRISK特征点也存在很大程度的减少，而Harris-Laplace角点随着尺度增大检测数量相对稳定，能有效适应尺度变化，但从效果图中可以看出存在许多重复的特征点，而且有效角点太少。Harris-Laplace和BRISK算法在多尺度金字塔上进行角点检测，可以看出很多的特征点具有重复的特征尺度，会出现很多的冗余点。而本文模型的多尺度FAST角点随着图像尺度变化，角点检测数量并没有出现下降，而且仍然能保持准确的角点定位，在发生较大尺度变化的图像依然能检测到大量的有效角点。

图8 尺度变化下的FAST角点

图9 尺度变化下的Harris-Laplace角点

图10 尺度变化下的BRISK特征点

图11 尺度变化下的多尺度FAST角点

图12 不同角点算法检测的角点数量

本文的多尺度FAST角点的自适应作用域能够根据不同尺度的图像选择对应大小的作用域。对发生尺度变化的图像，基本的FAST角点半径为3的圆形作用域不能覆盖到有效灰度差异的区域。而本文的尺度信息熵模型可以计算发生尺度变化的图像的相对高斯模糊器尺寸，以此尺寸参数作为新的作用域半径，即自适应作用域，这样就能覆盖到有效灰度差异的区域从而检测出符合FAST角点策略的特征点。同时在本文的算法流程中，在已经得到的尺度信息熵模型基础上，对实际应用中的图像仅需计算其梯度图像信息熵，计算相对尺度参数并在查询表中获取适应的作用域参数，最后根据FAST角点策略进行角点检测，相比其他多尺度算法中构建尺度金字塔等算法流程，本文算法效率更高，计算更简单。

5 结 语

本文根据图像尺度变化和信息熵的变化关系拟合出了幂函数表达式的尺度信息熵模型，并基于该模型提出了多尺度FAST角点。尺度信息熵模型能够有效地反映图像的尺度变化与梯度图像信息熵的函数关系，而基于该模型的多尺度FAST角点的自适应作用域能够有效地适应发生尺度变化后的图像局部区域的灰度变化，从而提取有效的FAST角点，相比基本的FAST角点和其他多尺度角点算法，其尺度适应性更好，算法流程更简单。同时，本文基于尺度信息熵模型的多尺度改进方法，同样适用于其他具有固定作用域的特征点算法，在图像多尺度应用方向具有很好的使用价值。本文的尺度信息熵模型会受到拟合实验的限制，由于实验图像类型不够全面，模型泛化能力不够优秀，所以为了提高尺度信息熵模型的准确性还需要进行多方面的拟合实验。