基于TSVD的高阶图像低秩近似新方法

杨 洁 魏平俊 廖 亮

(中原工学院电子信息学院 河南 郑州 450007)

0 引 言

随着现代多媒体技术与计算机技术的迅速发展，超大规模、超复杂结构和高维度的数据分析与处理成为研究重点。如人脸图像、监控视频、高光谱图像等[1-5]。高维数据分析已成功应用于不同场景，包括生物医学图像分析[6]、自然图像和视频分析[7]和遥感图像分析[8]。目前，国内外学者在此研究基础上完成了许多工作。Zhang等[9]开发了张量辨别局部对齐方法，从高光谱图像中去除冗余信息。Zhong等[10]提出一种辨别张量光谱空间的特征提取方法，提高分类性能。Tao等[11]提出一种基于张量分解技术的用于极化SAR数据分类的张量ICA特征提取方法。

上述的研究工作均是在传统矩阵或三维张量的基础上开展的，并未针对高阶图像进行分析，不涉及三维以上的高阶数组，从而忽略了图像原本的结构特点。本文提出基于广义奇异值分解的高阶图像低秩的改进方法，在传统矩阵的基础上利用“tproduct”模型分析高阶数组[12]，并对传统矩阵算法进行扩展，得到适用于高阶广义复数矩阵的广义奇异值分解算法，再对高阶图像进行低秩近似分析其性能。

1 广义复数矩阵

传统的向量和矩阵分别代表一阶和二阶数组，而高阶数组是将传统矩阵中的标量元素扩展为广义标量(tensorial scalar，t-scalar)。广义标量是一个固定大小的数组，以广义标量为元素组成的矩阵称为广义矩阵(tensorial matrix，t-matrix)。广义矩阵是在传统矩阵的基础上，以矩阵中的每个元素为中心点逐步选取邻域，然后将选取邻域作为广义标量替换原位置的实数，目的是使原始二阶矩阵扩展为高阶广义矩阵。

广义复数矩阵是对广义实数矩阵的扩展，是一种高阶复数矩阵。广义复数矩阵是指在高阶广义矩阵中的每个元素皆为复数。定义一个N阶广义复数矩阵A∈CL1×L2×…×LN，其中:C表示复数域;Li表示第i阶广义矩阵的长度，且Li>1，i=1,2,…,N。这里定义广义复数矩阵的元素为(Xtm)w1,w2,i,j，且均为复数。

复数域C上的N阶数组是集合C≡CL1×L2×…×LN中的一个元素，实数域R上的N阶数组是集合R≡RL1×L2×…×LN中的元素，这里定义C或R均为交换环结构，且乘积用循环卷积替代[13]，在广义复数矩阵运算中，定义所有的运算都是在环C中进行。

1.1 符号和定义

定义1广义复数标量乘法：任给定广义复数标量xt∈Cm×n和yt∈Cm×n，定义两者乘积dt=xt∘yt是由xt和yt做二维循环卷积所得，满足:

(1)

且p=(mod((ω1-k1),m)+1,mod((ω2-k2),n)+1),∀ω1,ω2，其中(ω1,ω2)代表广义复数标量中元素坐标，因空域做循环卷积步骤较复杂，这里可将其简化为利用dt=xt∘yt⟺[F(dt)]ω1,ω2=[F(xt)]ω1,ω2·[F(yt)]ω1,ω2,∀ω1,ω2。通过二维快速傅里叶变换及其逆变换来求得计算乘积dt，广义复数标量乘法具体如图1所示。

图1 广义复数标量乘法

其中广义t-scalar中的元素均为复数，即aw1,w2,bw1,w2,cw1,w2∈C。

[Ctm]i,j=[Xtm]i,j+[Ytm]i,j1≤i≤D11≤j≤D2

(2)

定义3广义复数矩阵的乘法：任给定广义复数矩阵Xtm∈CD1×D2和Ytm∈CD2×D3，其乘积由Ctm=Xtm∘Ytm∈CD1×D3给出，满足：

(3)

如Ctm=Xtm∘Ytm，且D1×D2=2×2,D2×D3=2×1，定义t-scalar为3×3的广义复数标量，则Ctm∈C3×3×2×1。其中(Ctm)w1,w2,i,j根据定义1计算可得，广义复数矩阵的乘法如图2所示。

图2 广义复数矩阵的乘法

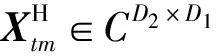
(4)

同时可得出:

(5)

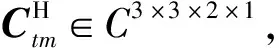
定义5广义复数矩阵的切片：任给定广义复数矩阵Xtm，它的项是m×n的广义复数标量，根据广义复数标量中元素的坐标(ω1,ω2)，得到切片Xtm(ω1,ω2)∈CD1×D2，为传统复数矩阵:

[Xtm(ω1,ω2)]i,j=[[Xtm]i,j]ω1,ω2∀i,j,ω1,ω2

(6)

令Xftm≐F(Xtm)按索引(ω1,ω2)的切片为Xftm(ω1,ω2)且Xftm(ω1,ω2)∈CD1,D2,满足：

[Xftm(ω1,ω2)]i,j=[[Xftm]i,j]ω1,ω2∀i,j,ω1,ω2

(7)

1.2 SVD原理

给定一个m×n阶矩阵A，矩阵中的元素aij∈C(i=1,2,…,m;j=1,2,…,n)。利用SVD分解，矩阵A可以表示为[14-15]：

A=USVT

(8)

式中：U∈Cm×m、V∈Cm×n均属于正交单位矩阵，即UUT=VVT=I;S是对角方阵：

(9)

式中:r=min(m,n)；σ1≥σ2…≥σr≥0,成为矩阵A的奇异值元素[16]。A也可以用求和的形式表示为：

(10)

式中：ui、vi是U和V的第i列向量;si是构成S矩阵对角线的奇异值。

1.3 TSVD原理

奇异值分解技术在线性代数中不可或缺，是一种重要的矩阵分解技术，通过一维信号能构造出多个矩阵，例如Cycle矩阵、Toeplitz矩阵、Hankel矩阵等。构造的方式不同，得到的SVD处理效果就不同。为得到更高的图像质量，本文通过扩展数据容量，构造高阶矩阵来进行SVD 分解，称为广义奇异值分解技术。广义奇异值分解是对传统矩阵上的每个元素取3×3邻域使其扩展成高阶矩阵。广义奇异值分解不仅适用于实数矩阵，对复数矩阵同样适用，具体原理如下：

任给定广义复数矩阵Xtm∈CD1×D2，t-scalar大小为m×n，利用TSVD分解，矩阵Xtm可表示为：

(11)

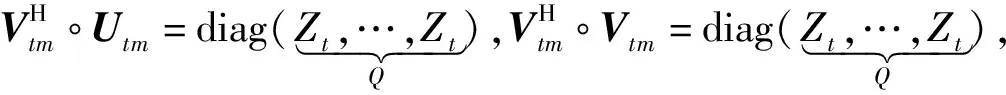
在对高阶图像进行分析时，可借助切片操作，在傅里叶域中通过传统SVD来计算。具体地，给定广义标量矩阵Xtm∈Cm×n×D1×D2,可用算法1计算式(10)。

算法1TSVD算法

1.Xftm←F(Xtm)

2.forω1←1 tomdo

3. forω2←1 tondo

4. 利用切片Xftm(ω1,ω2)计算Xftm的标准SVD分解，利用式(8)得到：

A=U·S·VH

其中U∈CD1×Q，V∈CD2×Q，S∈CQ×Q，Q≐min(D1,D2),VH是复数矩阵V的共轭转置。

5. 分配广义复数矩阵的第(ω1,ω2)个切片，

6.end for

7.end for

8.return

2 实 验

为验证TSVD的低秩近似性能，实验以480×300×3的Mona Lisa图像为测试样本，通过MATLAB编程分别得到R、G、B三幅二维灰度图像，这里以R通道的灰度图像为例。本文主要进行两方面的实验：(1)将传统二阶矩阵扩展为高阶的广义复数矩阵；(2)改变高阶矩阵的扩展方式，由原始的线性增长扩展为指数增长(Exponential Growth)方式，然后利用Latex编程比较TSVD的低秩近似性能。

2.1 高阶广义复数矩阵与指数增长

将传统二阶矩阵扩展为高阶的广义复数矩阵，具体的扩展方法有：(1)在传统矩阵的基础上通过变换使其成为二阶复数矩阵，再扩展为高阶广义复数矩阵；(2)先使传统矩阵扩展为广义矩阵，在广义矩阵的基础上通过变换使其成为广义复数矩阵，再用指数增长代替原始的线性增长方式。

1)传统矩阵到广义矩阵再到广义复数矩阵：实验均选取3×3邻域，在对奇数矩阵求傅里叶变换时存在镜像对称关系，为避免这种情况这里选取另一种方式进行扩展：在邻域选取时先将t-scalar利用镜像对称关系转为广义复数t-scalar，再作用于传统矩阵Xtcom∈R3×3×m×n，使其扩展为广义复数矩阵。镜像对称下t-scalar的选取如图4所示。

图4 镜像对称下t-scalar的选取

2)传统复数矩阵到广义矩阵再到广义复数矩阵：在传统矩阵的基础上进行变换使其成为二阶复数矩阵，然后再扩展为高阶的广义复数矩阵。具体实现原理为：保留原始矩阵，并对其求邻域，将原始矩阵和领域矩阵作为实部和虚部并重新组合成二阶复数矩阵。具体步骤是：对原始二阶矩阵A∈Rm×n求左(右，等)邻域，得到新的二阶实数矩阵B∈Rm×n，然后利用C=complex(A,B)，求得原始二阶矩阵和新的二阶实数矩阵组成的二阶复数矩阵Acom∈Rm×n，再对Acom进行扩展使其成为高阶广义复数矩阵Xtcom∈R3×3×m×n，邻域法选取如图5所示。

图5 邻域法选取

指数增长：指一个变量增长的速率与它的数量成比例，形如：y=ax(a>0,a≠1),x∈R。利用指数增长方式可快速提高图像的维数与低秩近似的效果。

2.2 实验结果分析

本文共进行8个实验：实验1是针对传统的2阶矩阵求SVD；实验2是保留原始矩阵，并对其求左邻域，将原始矩阵和领域矩阵作为实部和虚部并重新组合成2阶复数矩阵；实验3是在实验1基础上，对各元素求3×3邻域使其成为广义实数矩阵；实验4是利用镜像对称关系进行t-scalar的选取，并扩展为广义复数矩阵；实验5是在实验2的基础上对各元素求3×3邻域使其成为广义复数矩阵；实验6是在实验5的基础上再对各元素选取3×3邻域，使其成为6阶广义复数矩阵；实验7是在实验1 的基础上，将传统2阶矩阵元素通过选取3×3邻域使其成为4阶广义矩阵，然后再在4阶广义矩阵的基础上选取3×3邻域使其成为6阶广义矩阵；实验8是利用指数增长的方式，在实验7中扩展为4阶广义矩阵时，利用指数增长的方式对各元素选取3×3×3×3邻域使其成为8阶广义矩阵。然后利用TSVD技术，对比不同方式扩展后的低秩近似图像，并求取中心切片再利用峰值信噪比比较低秩近似性能，这样可以看出它们的差异。

主要通过对比实验1和实验2来分析比较实数矩阵和复数矩阵TSVD低秩近似性能的最优方案，实验数据如表1和图6所示。

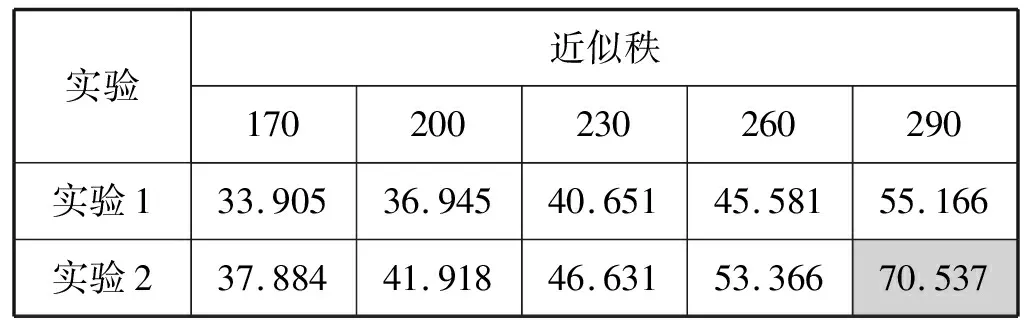
表1 复数矩阵

图6 实验1和实验2对比结果

由实验数据可知，复数矩阵的低秩近似性能要高于实数矩阵，同时得出选取左邻域来扩展传统矩阵具有更高的低秩近似性能。将二阶矩阵的t-scalar进行高阶扩展得到高阶广义复数矩阵，并对得到的广义复数矩阵再选取3邻域得到更高阶广义复数矩阵，如实验3至实验6，并分析其低秩近似性能，得到结果如表2和图7所示。

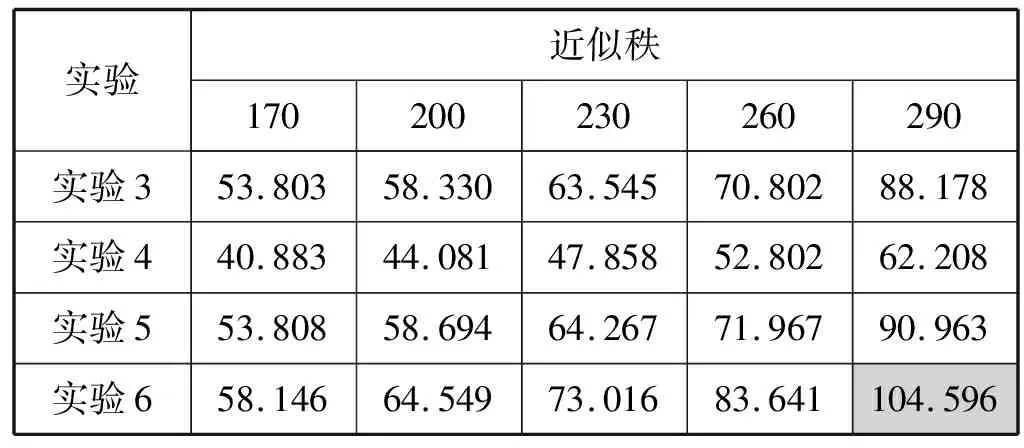
表2 高阶复数矩阵

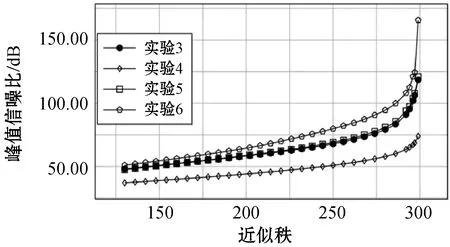
图7 实验3至实验6高阶复数矩阵对比结果

由实验数据可知，广义实数矩阵的低秩近似效果要高于利用镜像对称关系进行t-scalar的选取扩展为广义复数矩阵的近似效果；而通过对各元素求3×3邻域增加t-scalars的阶数所形成的广义复数矩阵的低秩近似效果要高于高阶实数所求的峰值信噪比，且峰值信噪比与t-scalars的阶数成正比关系。

另一种扩展方式为指数增长，以Mona Lisa图像为样本，在传统矩阵的基础上对各元素以线性增长方式与指数增长方式求3×3或3×3×3×3邻域，比较利用线性增长方式与指数增长方式扩展后图像的低秩近似效果，实验结果如表3和图8所示。

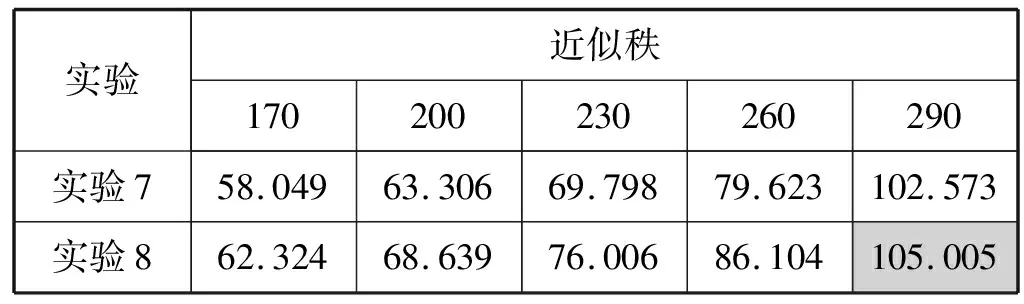
表3 线性增长与指数增长方式扩展后的低秩近似效果

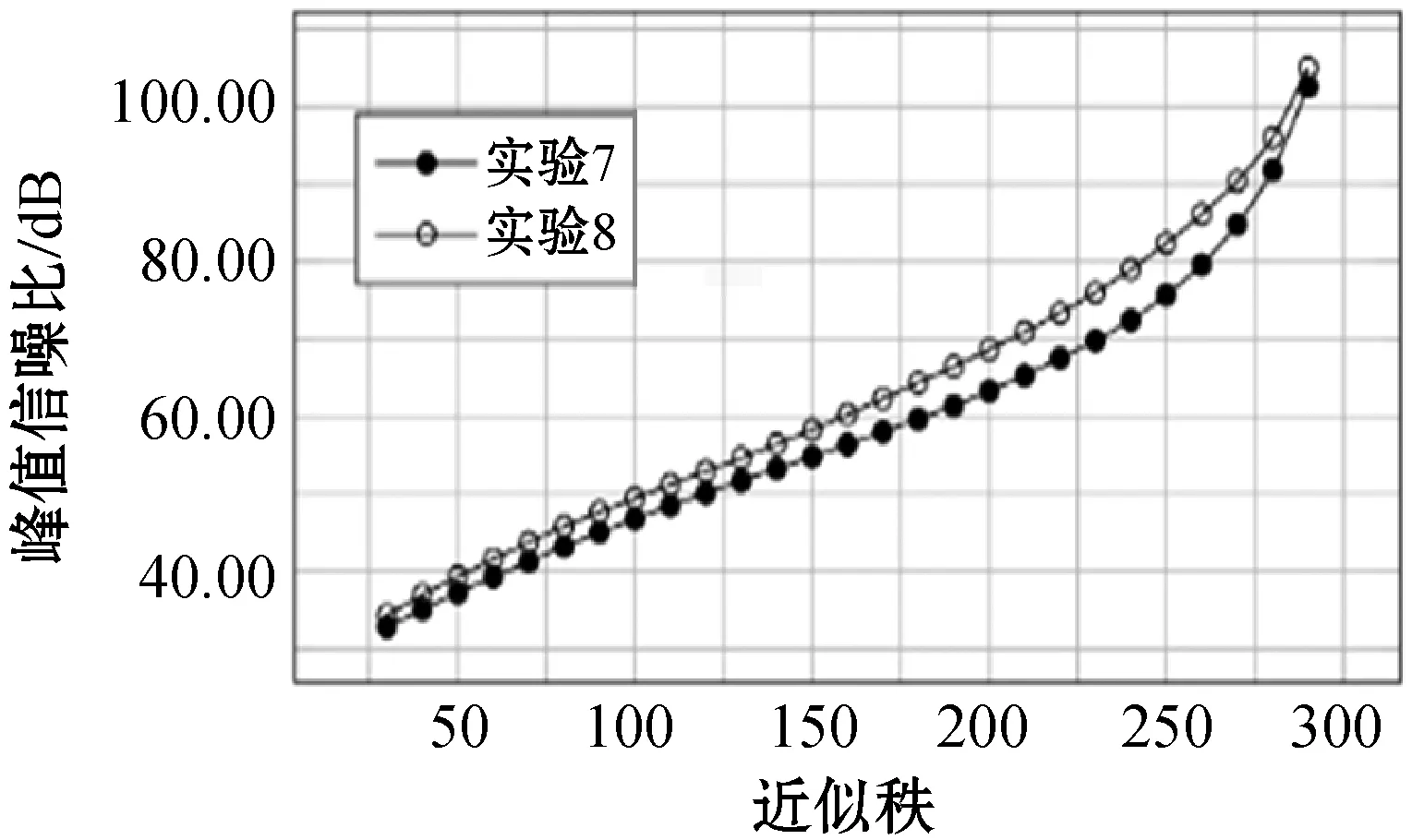
图8 线性增长与指数增长方式近似效果

由实验数据得出，在传统矩阵的基础上对各元素求左邻域，将原始矩阵和领域矩阵作为实部和虚部并重新组合成二阶复数矩阵，并以指数增长的方式对各元素求3×3邻域或3×3×3×3邻域，可得到最优的低秩近似结果。

3 结 语

为证明所采用的广义复数矩阵在高阶图像分析中的应用，本文通过实验分析广义矩阵算法和广义复数算法，将原始线性增长方式改进为指数增长，再进行低秩近似和重建。实验数据表明，在高阶图像分析方面，广义复数矩阵算法与实数矩阵算法相比，图像的低秩重建效果更具有明显的优越性，指数增长方式与线性增长方式相比亦具有明显的优越性。将其应用于高阶图像分析，易得出在二阶复数矩阵的基础上以指数增长的方式扩展为高阶广义复数矩阵可得到最优的低秩近似结果。