浅谈用传统文化知识激发学生学习数学的兴趣

张卫峰

美国心理学家布鲁纳曾指出：“对学生最好的刺激乃是对所学教材的兴趣”。由于数学是一门具有高度抽象性、严谨逻辑性的学科，有的教师在教学过程不注意方法，是很多学生失去了学习数学的兴趣。作为数学教师，利用中华民族历史长河中孕育了灿爛独特的民族传统文化，挖掘传统文化与数学教材知识中的结合点，让学生利用已有的数学知识经验，使数学与传统文化相联系，使其产生对数学的好奇心和求知欲，激发学生学习数学的兴趣。下面就从三个方面为例来探索。

1.利用九宫图（有名三阶幻方）为例。

在人教版七年级数学第一章《有理数加法》运算这节课中，我们可以用电视剧《射雕英雄传》中，神算子瑛姑考黄蓉“九宫图”，黄蓉说出：“九宫之义，法以灵龟，二四为肩，六八为足，左三右七，戴九履一，五居中央”这段的视频作为情景进行引入新课，就能吸引学生的注意力，激发了学生学习本节课的兴趣。

人教版七年级数学第一章《有理数加法》运算这节课， 多次安排了在 3×3的小方格里填数的练习题. 其中， 把 1、2、3、4、5、6、7、8、9这九个自然数填进小方格，并且使图中各行、列及斜对角的三个数字之和都相等的图形， 叫做九宫图，如图所示。教室装有多媒体设备的学校，可以给学生展示图1这幅图片，让学生对数学产生好奇心，培养他们观察分析问题的能力，就会激发学生学习数学的兴趣。

随着现代教育技术和网络的普及，学生获得知识方面更强更广泛，在上完课后，可以让学生回家后用电脑查阅幻方的相关资料，教师可以引导学生，让学生自己提出问题，让学生查资料解决问题，培养学生探索问题和观察思考问题的能力。例如下面几个问题：

1.1 三阶幻方的填法和构造法出自我国古代那些书籍呢？

1.2  为何九宫图各行、列及斜对角的三个数字之和为15，15是怎么算出来的？15与中心数5有和关系？

1.3九宫图还有几种形式？除过上图的形式，还有几种变式？请把变式都写出来？

1.4九宫图所有形式中五个奇数和和四个偶数的位置的共同点？

1.5九宫图所有形式中各行、列及斜对角三个数的差是啥关系？

2.利用八卦图为例。

在北师大版高中数学教材必修1中，第69页的《正整数指数函数》一课中的“实例分析”问题1：细胞分裂时，，由1个分裂成2个，2个分裂成4个……一直分裂下去，其中一个问题为列表表示1个细胞分裂次数分别是1，2，3，4，5，6，7，8时，得到的细胞个数。教师讲授本节课时可以用多媒体展示“太极生两仪，两仪生四象，四象生八卦”的过程来引入新课，这样是学生更加容易理解知识，从而能很好的掌握知识，是传统文化和教材很好的结合起来，让学生产生学习数学的兴趣。

《易经》中的“太极生两仪，两仪生四象，四象生八卦”，这句话中就蕴含着数学的文化知识。意思就是说太极分裂成两仪，两仪分裂成四象，四象分裂成八卦。用数学观点可以理解为， 就是一个变二个，二个变四个，四个变八个，这句话中的三个“生”可以理解成数学中变化的过程，就可以把这个问题转化成正整数指数函数模型的问题研究。在这个问题中蕴含着几个数学知识，我们就引导学生挖掘出来，就从以下三个方面来看一下。

2.1正整数指数函数的知识：y=（n=0， 1， 2， 3）.在这就是一个自变量n为正整数0，1，2，3的正整数指数函数。

（1）n=0，  y=1; （2） n=1， y=2，   （3）n=2，  y=4;  （4）n=3，  y=8

2.2 等比数列的知识：（图形个数比）

1个太极图形， 2个两仪图形， 4个四象图形， 8个八卦图形。从一个数开始，后一个数比前一个数的比值都是一个常数，那么这个数列就叫等比数列。

2.3等比数列求和的知识：（图形个数和）

1个太极图形+ 2个两仪图形+4个四象图形+8个八卦图形=15个不同的图形。

3.利用公元纪年法和成干支纪年法为例。

在初中历史课本中会遇到一些重要的历史事件，例如甲午战争、戊戌变法、辛亥革命等。学生不知道怎么命名，这些问题是涉及到两种纪年法——公元纪年法和干支纪年法的问题。为此，以数学观点来阐述这个问题。

3.1让学生知道干支纪年的有关初步知识。

3.1.1首先关键就在先弄懂什么是天干与地支。

天干有10个，即甲、乙、丙、丁、戊、己、庚、辛、壬、癸;

地支有12个，即子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥

3.1.2弄懂什么是天干与地支排列组合规律。干支是天干和地支的合称。

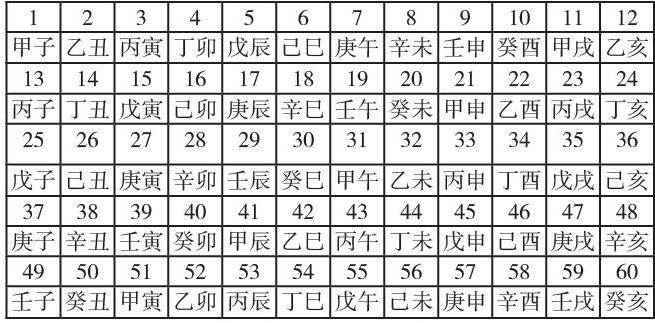
天干和地支从“甲子”开始，按顺序逐一相配，各用到最后一个时，再从第一个开始继续相配，从而形成了 60 个干支，也称“六十花甲子”。周而复始，循环记录，这就是俗称的“干支纪年”。这里蕴含了数学中的排列组合知识。

3.2六十花甲和干支纪年里蕴含的数学知识。

天干10个，地支12个，10和12的最小公陪数就是60，这就是六十花甲中的六十的来源，学生就很明白原来用数学中的最小公陪数的知识理解。

天干与地支排列组合，是高中数学知识的组合知识，不是排列知识。干支纪年中也蕴含了周期现象的数学知识。

三阶幻方、八卦图和公元纪年法换算成干支纪年法是很难得的好教材. 它对于培养学生学习数学的兴趣，热爱数学， 热爱生活， 勤于思考， 勇于探索，并学会如何观察问题， 如何发现问题， 如何转化分析， 如何证明结论， 如何总结提炼都有重要作用， 老师们应当尽力挖掘教科书的潜在教育功能， 既注意眼前的近期目标， 又注意未来的长远目标。