一种类电磁机制算法在锅炉主汽温系统的研究
2020-10-14张雅雯
周 斌, 陈 晶, 张雅雯, 薛 东
(安徽电气工程职业技术学院,安徽 合肥 230051)
当前发电厂普遍采用大容量、高参数机组,对控制系统的控制要求相对较高,其中机组主汽温度控制是一个常熟常新的研究课题。主汽温控制系统在实际运行中要求温度变化范围向上不超过5℃向下不超过10℃。科研学者将各种新兴的智能控制算法应用于主汽温系统中,类电磁机制算法就是2003年提出的智能优化算法,其原理简单,收敛速度快,全局优化性能显著,本文对其进行深入研究,对算法的不足之处进行改进,针对单元机组主蒸汽温度控制系统被控对象的特点,选取具有代表性的数学模型,用改进的类电磁机制算法对主汽温控制系统控制器参数进行仿真优化。
1 传统的类电磁机制算法
传统的类电磁机制算法首先参照人为制定的规则计算粒子的带电量的多少,然后根据静电力计算法则对粒子的受力情况进行分析,最后根据力的合成法则计算解空间中的每个粒子(问题解)受到的合力,所有粒子在合力作用下沿着合力方向进行位置移动更新,根据精度要求制定算法的终止条件,经过有限步的迭代运算,最终在满足终止条件的基础上求出目标函数的全局最优值[1]。
2 类电磁机制算法的改进
2.1 初始种群
传统的类电磁机制算法构建初始化种群,由于粒子的产生的随机性,高维度的函数可能导致算法陷入局部最优,为避免这种情形的发生,使用夹角余弦的定义构造算法的初始种群,夹角余弦的取值范围为[-1,1],余弦值与夹角大小存在负相关关系,所以本文用夹角余弦来衡量种群中粒子间的相似度,在空间概念上区分粒子之间的差异,在初始化种群的过程中,限定个体间的夹角余弦范围[-1,0.5],保证粒子相互之间的差异性的存在,同时能够使粒子在初始种群中分布的均匀性。

生成M个粒子,初始化种群population=X,种群规模size=M,问题维度dim=N
1:定义一个数组pop(M,N);
2:int i,M;
3:random generate a individual a1;pop(1) a1
4:for i=2 to M
5:generate a individual ai;
6:calculate cos(a1,ai)
7:if (cos(a1,ai)<0.5) pop(i) ai
8:else delete and renew ai返回step5
9:end if
10:end for
11:return pop
2.2 引入决策因子和变异因子的双因子局部搜索算法
局部搜索算法也就是说在一个较小的邻域内搜索比当前粒子适应值更小的粒子,并进行循环替代的过程,为了减小算法的时间复杂度,提高算法的收敛速度,在算法的局部搜索这一步骤,将对当前最优的粒子进行,对局部搜索算法做如下修改[2]:
(1)随机选定2个变量αβ∈(0,1)。定义α为决策因子,β为变异因子;
(2)局部最优解更新。定义如下:若α≥0.5,r1=xbest+β(μk-xbest);否则,r2=xbest-β(xbest-lk);
2.3 粒子合力计算简化
类电磁机制算法中粒子xi所带电荷量Qi的大小决定了其吸引力或者排斥力的大小,传统类电磁机制算法中粒子的电荷量计算公式如式(1):
(1)
合力的计算公式如式(2):
(2)
针对电荷量和合力计算方面存在的弊端,将合力计算式(2)改进为式(3):
(3)
2.4 基于自适应步长修正因子的粒子位置更新
作者对粒子更新规则改进如下:
粒子位置更新:
(4)
3 基于改进类电磁机制算法的PID参数优化及其仿真
某300MW火电机组锅炉60%负荷下,控制系统框图如图1所示。
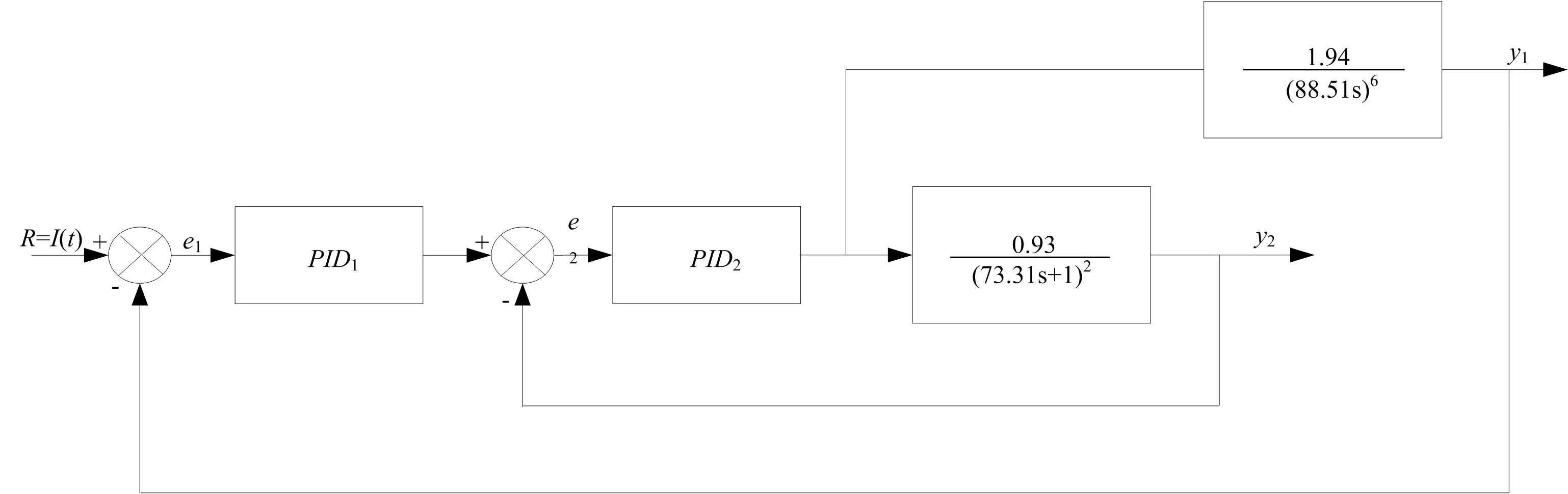
图1 主汽温串级控制系统框图
PID依然是目前工业现场主流的控制器, 其典型传递函数如式
(5)
对于火电厂控制系统,系统运行过程经常采用经验试凑法整定PID的参数,长期的实践表明,经验的PID参数能满足系统的品质要求。故可将经验值选定为类电磁机制等优化算法的初值数据,根据这个数据计算出参数区间,以减少计算寻优时间。
约束条件:Mp<15%,tr<500,ts<1500,0.76<φ<0.98
优化参数的论域选为:δ1∈(1,5),ti1∈(50,400),δ2∈(0.1,1),Ti2∈(50,150)
选取稳定工况下60%负荷主蒸汽温度对象模型,使用改进的类电磁机制算法对内外回路的PI控制器参数δ1,Ti1,δ2,Ti2 4个参数寻优。种群规模取100,最大迭代数取100,局部最大迭代次数取20,待优化4个参数的区间上限为[5,400,1,150],下限为[1,50,0.1,50]。优化得到的PID参数结果为δ1=1.1587,Ti1=288.2909,δ2=0.2276,Ti2=50.1650=50.1650。优化后的主蒸汽温度单位阶跃响应如图2所示,品质指标为衰减率为0.816、超调量16.1%、。同理获得45%、75%负荷主蒸汽温度对象模型的单位阶跃响应曲线如图3所示。
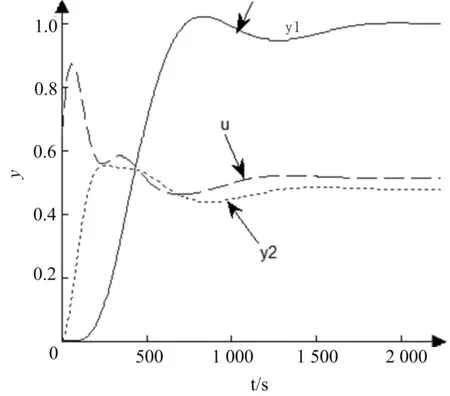
图2 60%负荷单位阶跃响应曲线

图3 3个稳定工况点优化对比分析图
从优化结果来看,控制品质达到了设计要求,利用改进的类电磁机制优化算法整定的主汽温串级控制系统的品质性能较好,负荷波动时的单位阶跃响应显示该系统具有较强的鲁棒性[3]。
4 结束语
本文所研究的基于改进类电磁机制算法的主汽温控制系统优化取得了很好的控制效果,此方法原理简单、方便实施,是一种值得关注并应用的策略。
