基于深度玻尔兹曼机的并行电力负荷预测算法

杨 鹤，王 良，修世军

(辽东学院 现代教育技术中心，辽宁 丹东 118001)

当前是一个智能电网飞速发展的时代，智能电网将传统的电力系统与最新的信息技术有机的结合在了一起。在电网运行过程中，产生的大量数据成为了故障检测与诊断、调度策略选择、智能控制决策等方面的重要依据。

电力系统是一个典型的动态非线性系统，由于人工神经网络优异的非线性处理能力，已经在电力系统得到了广泛的研究与医用。葛少云等在给定实时电价的条件下，使用灰色神经网络建模，并用遗传算法进行优化，对短期电力负荷进行了预测[1]。雷绍兰等在不考虑电价的情况下，利用RBF神经网络进行了短期电力负荷预测，并使用ANFIS算法进行了修正[2]。杨光亮和石东源等分别应用小波神经网络和RBF神经网络实现了电力系统的故障检测[3-4]。2006年Hinton等人引发了深度学习的热潮[5]，随着对深度学习研究的展开，研究人员开始将深度学习应用到智能电网中。Tarsa等使用深度信念网络进行了短期的电力预测[6]。Zhu等采用分层稀疏编码对电路的电能消耗进行了预测[7]。也有一些研究者对单隐层的神经网络并行化进行了研究[8-9]。

然而，在大数据环境下，传统的研究与应用还面临以下问题：

(1)数据量大，数据维度高；(2)模型结构日趋复杂；(3)实际应用中，对预测数据的需求存在动态变化。传统模型的训练过程往往需要10几个小时乃至几天的时间，每次建立新的模型都需要漫长的等待过程，这在电网策略更加细化、动态化的条件的是不能容忍的。

因此，本文提出基于MapReduce的智能电网多层感知器并行训练算法研究。将电网的预测模型训练过程并行化，充分利用云计算提供的强大计算能力，缩短计算时间。另外，神经网络的训练是一个多次迭代的过程，传统的MapReduce技术并不善于处理迭代计算，针对这一问题，本文还采用了IMapReduce技术对迭代计算进行了优化，每次作业结束后会先对结果进行缓存，直到整个迭代过程全部结束才上传结果到集群的分布式文件系统。同时，每次迭代获得的中间结果被缓存到运算节点本地，只有更改的状态才会上传到分布式文件系统，因此可以取消传统算法中部分作业，解决训练过程中频繁迭代的问题，节省大量运行时间。最后，在由多台PC组成的集群中进行了实验。

1 使用多层感知机进行预测

1.1 受限玻尔兹曼机

玻尔兹曼机是一种由随机神经元组成的二值随机机器，它的神经元取值有0和1两种状态，分别存在不同的概率，其中0代表神经元处于关闭或者不连通的状态，1代表神经元处于打开或者联通状态。玻尔兹曼机的神经元被分为2类，分别是可见单元V={vi}和隐藏单元H={hi}。其中可见单元包括输入节点和输出节点，是外部环境与模型之间的接口。隐藏单元可以从数据中提取特征。神经元之间的连接都是对称的，当连接只存在于可见单元与隐藏单元之间时，就被成为受限玻尔兹曼机。通过各个神经元的状态可以计算出整个模型的能量E，如(1)所示：

(1)

其中wij表示两个神经元之间连接的权重，θ={W,a,b}表示模型的参数。

神经元状态的联合概率可以通过神经元状态、能量E和玻尔兹曼分布来求得，如(2)所示

(2)

其中Z(θ)如(3)所示

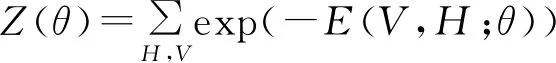
(3)

由此可以得出最大对数似然函数如(4)所示

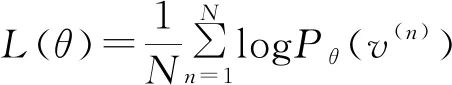
(4)

使其对W求导，就可以得到参数的更新规律如(5)所示

△W=ε(Epdata[vihj]-Epθ[vihj])

(5)

其中ε表示学习率，Epdata表示数据的期望值，Epθ表示模型的期望值。

1.2 深度玻尔兹曼机

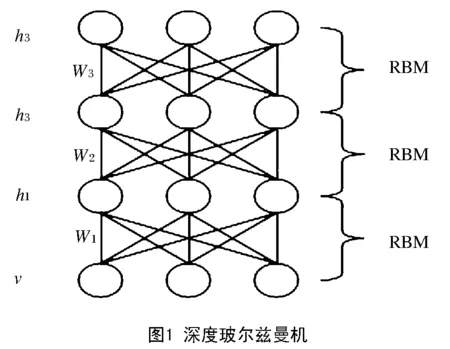
如果将多个受限玻尔兹曼机进行纵向叠加，就可以得到深度玻尔兹曼机，如图1所示。深度玻尔兹曼机只有在相邻的两层之间存在连接。图1所示的例子可以看做3个受限玻尔兹曼机的组合，由1个可见层v1和3个隐藏层h1、h2、h3组成。对深度玻尔兹曼机进行训练可以逐层进行，同时训练多个受限玻尔兹曼机然后再将它们组合在一起。

模型训练的过程被分为了2个部分，预训练与微调。以图1举例，预训练的步骤如下所示：

步骤1：受限将v1作为可见层，h1作为隐藏层构建一个受限玻尔兹曼机进行训练，训练过程中将v1到h1连接的权重设置为2×W1，h1到v1的权重不变。

步骤2：将h1作为可见层，h2作为隐藏层构建受限玻尔兹曼机，将权重设置为2×W2，进行训练。

步骤3：将h2作为可见层，h3作为隐藏层构建受限玻尔兹曼机进行训练，将h2到h3连接的权重设置为W3，h3到h2的权重设置为2×W3。

步骤4：最后，使用训练出来的{W1，W2，W3}构建一个深度玻尔兹曼机。

如果模型中有更多的隐藏层，可以多次重复第2步来进行计算。预训练结束后，再使用BP算法对模型进行微调。

2 基于MapReduce的并行训练算法

2.1 MapReduce框架

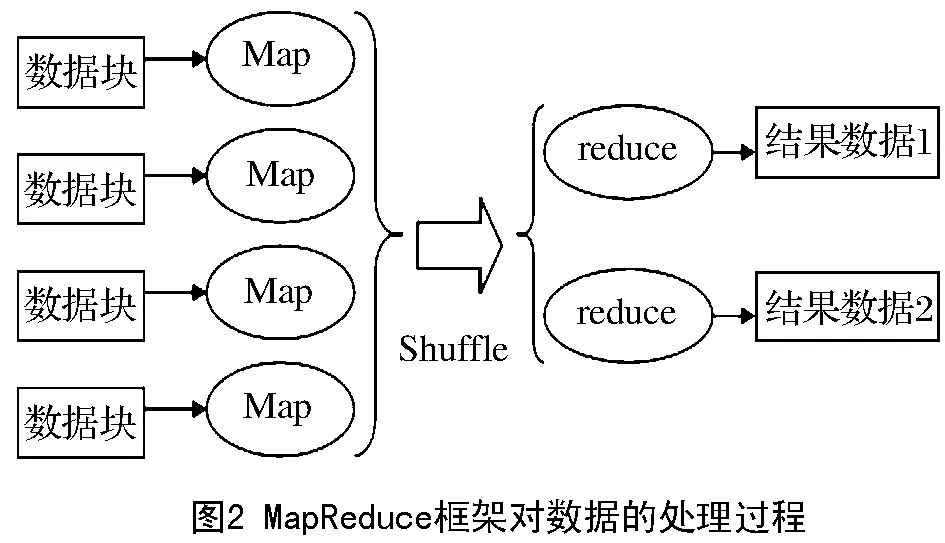
MapReduce是一种对数据进行批处理的并行计算框架。该框架适合于处理数据之间彼此独立，用户对于实时性要求不高的应用。因此，需要处理大量独立样本的神经网络模型学习过程正适用于MapReduce框架。该框架对数据的处理过程如图2所示，用户需要先将算法的逻辑划分成Map和Reduce 2个部分，2个部分都可以并行计算，分别用Map函数和Reduce函数进行封装；然后上传数据到集群，框架会将数据划分成等大的数据块分布式的存储在集群中，并且为每个数据块分配1个Map任务，在该任务中运行Map函数，这个过程是并行完成的；Map任务都结束后，通过shuffle过程进行同步，Map函数的输入会被分配给不同的Reduce任务；最后由Reduce任务输出结果。

2.2 MapReduce框架中的矩阵运算

矩阵运算是本文算法的核心内容，下面介绍在MapReduce框架中进行矩阵运算的算法。设有矩阵A=(aij)mn与矩阵B=(bij)nl，使用MapReduce计算C=AB。C是一个m×l阶矩阵，所以最后输出结果应该有m×l条数据。1个MapReduce作业可以完成1次矩阵乘法，也就是说只需要编写1个Map函数和1个Reduce函数。

首先，Map函数的输入为aij与bij，如果输入为aij，那么将输出l条数据<(i,k)，(j, ‘a’,aij)>其中(i,k)为Key值，k=1,2,3,…,l，(j, ‘a’,aij)位value值，字‘a’代表数据来自矩阵A。如果输入为bij，那么将输出m条数据<(i,k), (i,’b’,bij)>其中(i,k)为Key值，k=1,2,3，…，m，(i,‘b’,bij)为value值，字符‘b’代表数据来自矩阵B。

然后，经过shuffle过程，所有具有相同Key值的数据都被传输到同1个Reduce任务。Reduce函数的输入为<(i,j),list>，这样，计算aij所需的A矩阵第i行和B矩阵第j列数据都被存放如同1个list中，再根据矩阵的运算法则就可以计算出cij的值了。

矩阵加(减)法运算比较简单，设有矩阵A=(aij)mn与矩阵B=(bij)nl，使用MapReduce计算C=A+(-)B。Map函数读入aij与bij，输出时以(i,j)为Key，元素为值，在Reduce函数直接做加(减)操作。

2.3 基于MapReduce的训练算法

深度玻尔兹曼机的训练由多个受限玻尔兹曼机的训练过程组成，下文将首先介绍基于MapReduce的受限玻尔兹曼机训练算法，再介绍深度玻尔兹曼机训练算法。在MapReduce框架下进行训练与普通串行算法不同，需要将算法分为控制主函数、Map函数和Reduce函数3个部分，其中Map函数和Reduce函数主要用来进行矩阵运算，其算法在上1小节已经介绍，受限玻尔兹曼机训练算法主函数(简称为RMain)伪代码如下所示：

RMain算法：

输入：样本集合S，可见层数量nv，隐藏层数量nh，可见层到隐层倍数m，隐层到可见层倍数n。

(1)对学习率ε和连接权重矩阵W进行初始化；

(2)启动一个作业1，选择样本S中的样本si做矩阵乘运算h=siW；

(3)启动一个作业2，求更新参数p1ij=hj×si；

(4)启动一个作业3，计算显示层v等于hWT；

(5)启动一个作业4，计算h’=vW；

(6)启动作业5，计算更新参数p2ij=h’j×vi；

(7)启动作业6，更新W’=ε(p1ij-p2ij)；

(8)判读是否结束迭代，如果不结束则返回(2)；

在RMain算法的基础上，训练深度玻尔兹曼机，算法(简称DMain)伪代码如下所示：

DMain算法：

输入：样本集合S，可见层数量nv，隐藏层数量nh1、nh2、…、nhx

(1)调用RMain计算第一层RBM，

RMain(S,nv,nh1, 2, 1)；

(2)计算下一层RBM，RMain(S,nh1,nh2, 2, 2)；

(3)判断中间层是否结束，是进行第(4)步，否回到(2)；

混凝土浇筑完成后，及时进行养护，采用土工布或黑芯棉覆盖+洒水的方法，以土工布长期保持湿润为标准，由于顶板面预埋件较多，养护时采取土工布穿竖向精轧螺纹钢的方式，保证土工布紧贴混凝土面，保证养护质量，梁体内腔采用喷雾器，安排专人进行养护，按规范要求，养护时间不少于14d。当环境温度低于5℃时，梁表面喷涂养护剂，采取保温措施，禁止对混凝土洒水，混凝土喷涂养护剂养护时，应确保不漏喷；当外界气温较高时，适当增加洒水次数或延长洒水时间。

(4)计算最上层RBM，RMain(S,nh(x-1),nhx, 1, 2)；

2.4 对迭代计算的优化

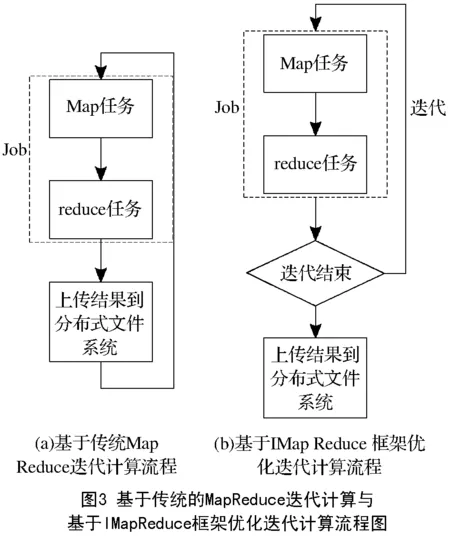
在对深度玻尔兹曼机进行训练的过程中，需要进行多次迭代。用传统的MapReduce进行迭代计算的流程如图3左所示，每一次迭代都被封装成一个或者几个作业(Job)。作业在启动后需要从分布式的文件系统中读取数据，作业结束后又将数据重新存入分布式文件系统。每一次存取都需要耗费大量的时间，当迭代次数较多时就会十分影响效率。针对这个问题，我们选择使用IMapReduce框架[10]进行了优化，其运行流程如图3右所示，每次作业结束后会先对结果进行缓存，直到整个迭代过程全部结束才上传结果到集群的分布式文件系统。这样可以节省大量运行时间。

在上1节的算法中存在大量的迭代过程，每一次迭代都包含若干个作业，虽然DMain算法利用并行计算能够处理大规模数据，但是运行效率依然不够理想。本节受限对作业进行优化整合，然后利用IMapReduce对迭代计算进行优化，优化过程如下：

步骤1：对RMain中的作业1和作业2进行了合并，在同一个Reduce任务中，计算出隐层h后同时计算参数p1;

步骤2：对RMain中的作业4和作业5进行了合并，在同一个Reduce任务中，计算出更新显示层v后同时计算参数p2;

步骤3：IMapReduce对原有的Map- Reduce接口没有改变，但是每次迭代获得的中间结果被缓存到运算节点本地，只有更改的状态才会上传到分布式文件系统。因此可以取消RMain中的作业6，同时需要在分布式文件系统中设置临时路径来保存状态的更改值。将上一节中的算法进行更新得到迭代优化的深度玻尔兹曼机训练算法IDMain，如下所示：

IDMain算法：

(1)设置状态路径

(2)调用RMain计算第一层RBM，

IRMain(S,nv,nh1, 2, 1)；

(3)计算下一层RBM，IRMain(S,nh1,nh2, 2, 2)；

(4)判断中间层是否结束，是进行第(5)步，否回到(2)；

(5)计算最上层RBM，IRMain(S,nh(x-1),nhx, 1, 2)；

IRMain算法：

输入：样本集合S，可见层数量nv，隐藏层数量nh，可见层到隐藏层倍数m，隐层到可见层倍数n。

(1)对学习率ε和连接权重矩阵W进行初始化；

(2)启动一个作业1，选择样本S中的样本si做矩阵乘运算h=siW,同时计算更新参数p1ij；

(3)启动一个作业2，计算显示层v等于hWT；

(4)启动一个作业3，计算h’=vW，同时计算更新参数p2ij；

(5)判读是否结束迭代，如果不结束则返回(2)。

3 实验与分析

3.1 实验环境

实验使用多台PC搭建了集群，其中一台作为master节点，其他作为slave节点。PC的配置为Intel(R) Core(TM)2 Duo E8200 dual-core 2.66GHz CPU、3 GB 内存、160 GB 硬盘，交换机为锐捷的千兆交换机。使用的操作系统为ubuntu11，使用了Apache开发的Hadoop1.0.3作为MapReduce环境以及开源工具IMapReduce。深度玻尔兹曼机网络共5层，包括1个可见层和4个隐藏层。

3.2 实验数据

为了进行测试，采集了北方某城市3个月的环境数据对电力负荷进行测试。由于实验数据量有限，本文对元数据集进行了扩大，数据集的描述如表1所示：

表1 数据集参数表

3.3 实验结果

本实验的计算量比较大，使用传统方式在单机运行的效率已经非常缓慢，因此直接使用了本文设计的IDMain算法。图4显示了在不同数量的节点上的运行时间，可以发现随着节点的增加，训练时间显著的缩短了。这次实验中使用了数据集DataSet1。

图5显示了使用传统MapReduce下的DMain算法和迭代优化的IDMain算法在处理不同数据集时的运行时间对比。本次实验使用了8台PC作为slave结点。在使用DataSet1时，IDMain运行时间是DMain的74%；在使用DataSet2时，IDMain运行时间是DMain的72%；在使用DataSet3时，IDMain运行时间是DMain的67%。可以发现随着数据集的增大，迭代优化的算法表现出更良好的性能。

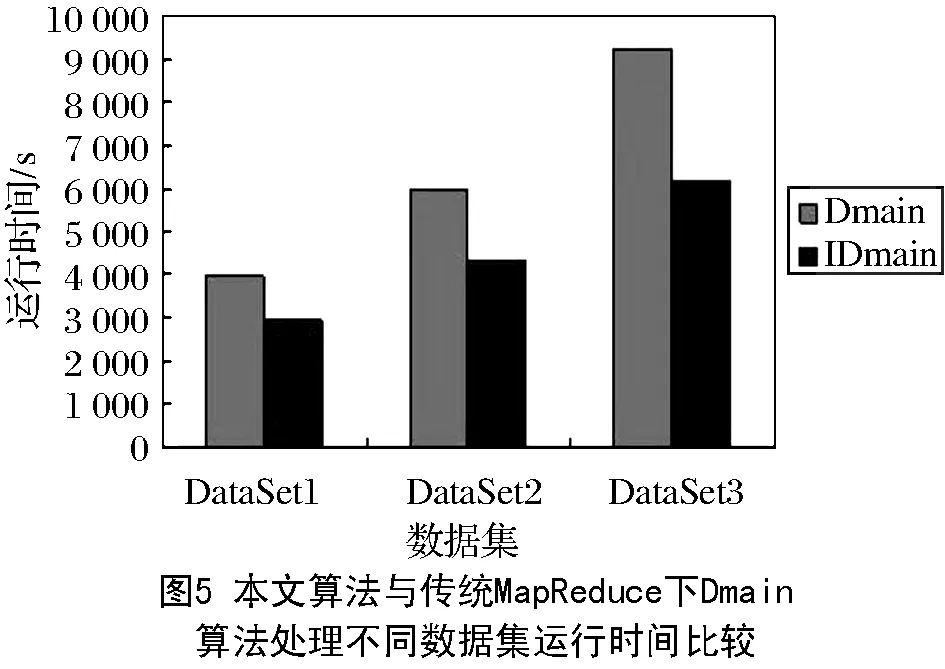
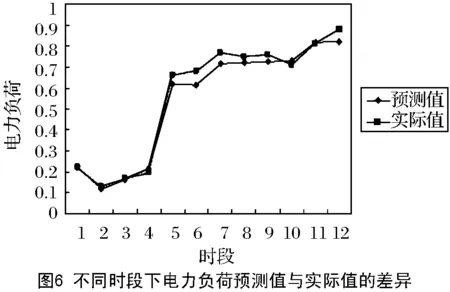
图6显示了进行归一化后，某日12个时段电力负荷预测值与实际值之间的差别。通过预测值与实际值之间的对比图可以看出，通过本算法计算出的结果与实际结果之间的差别较小，预测值已经可以逼近实际值。这是因为使用神经网络进行电力系统预测已经被证明是有效的，而通过本算法训练出的模型与传统方法训练出的模型在有效性方面是一致的。

4 结论

在智能电网中进行预测、故障检测是当前电力系统的一个重要研究方向。随着大数据技术的发展，对电力预测有了进一步推动。在该环境下，本文针对电网中大数据处理效率低、速度慢的问题进行了研究。提出了基于深度玻尔兹曼机的迭代优化的电力预测训练算法IDMain，并且搭建Hadoop集群进行了测试，实验表明，本文提出的算法在具有良好的性能和准确性。