岩石单轴压缩试验中能量演化分析方法

刘之喜，王 伟，罗吉安，缪广红

(1.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001; 2.安徽理工大学 煤矿安全高效开采省部共建教育部重点实验室,安徽 淮南 232001; 3.河海大学 岩土所，江苏 南京 210098; 4.安徽理工大学 力学与光电物理学院,安徽 淮南 232001)

热力学认为，物质受外部因素影响其尺寸、形状、密度等变化都是能量转化过程，在能量转化过程中失稳是材料破坏的本质原因，由此可知根据能量变化对岩石的破坏进行研究具有较强的工程及理论意义[1-5]。岩石的变形曲线是岩石热力学性质的某一方面的表现，是荷载作用下岩石的力学响应，所以基于岩石的变形曲线建立的本构模型及强度理论均不能够较好的反映岩石破坏的本质。从能量角度对岩石的力学响应进行研究，在岩石力学与工程领域引起了广泛的重视，并且取得了丰硕成果。

目前关于岩石能量的研究主要分为两方面:一是关于岩石受单轴或三轴荷载作用下峰前或峰后总能量的研究，以此建立岩石失稳条件、能量方面的本构模型以及岩爆预测;二是根据岩石在单轴或三轴的周期荷载下岩石的能量演化规律，对岩石的疲劳损伤、滞回效应等方面进行研究[6-12]。关于单轴或三轴压缩试验在能量方面的研究中谢和平等[13-15]从能量角度分析了岩石变形破坏过程中的能量演化及岩石强度的内在联系;杨凡杰等[16]基于能量耗散和释放角度提出了一个新的岩爆能量判断依据-单位时间相对能量释放率URLERI，在应用中计算结果与实际情况相吻合;李树枕等[17]对能量耗散弹性损伤本构及在工程中的应用进行了研究，运用耗散能不可逆推导了弹性损伤的等效应变和损伤屈服准则，建立了关于能量的弹性损伤模型。在第2方面的研究即周期荷载下岩石能量演化规律也取得了一些进展。刘建锋等[18]对细砂岩和粉砂质泥岩进行单轴压缩循环加卸载试验，研究结果表明岩石密度越大滞回环面积越小，发生的能量耗散也就越小。许江等[19]对孔隙水压力下砂岩的循环加卸载进行试验，探讨了变形损伤过程中能量吸收与释放的演化规律。赵洪宝和尹光志[20]对煤在循环荷载下的力学及不同荷载下的滞回环演化规律进行研究，随着循环荷载次数增多滞回环面积逐渐减小。肖福坤等[21]基于加卸载过程中滞回环的演化规律，提出了滞回环代表裂纹压密耗散能，基于循环荷载中的弹塑性能量进行了分析，对煤层抗冲击鉴定的弹性能量指数进行修正。

但是目前关于能量的研究中都是关于单轴、三轴压缩下总能量分析或循环加卸载过程中的弹性能、塑性能及滞回环等方面演化规律，而较少关于单轴压缩试验过程中能量演化趋势的分析，单轴压缩过程的能量分析有助于探索岩石在单轴压缩下压密阶段、弹性阶段、塑性阶段的能量演化趋势及能量分配，但是目前的试验手段无法得出单轴压缩试验过程中能量的具体演化趋势。为了探究岩石的能量演化规律，笔者假设疲劳损伤和裂纹间的界面摩擦产生的新裂纹对岩石的弹性能无影响。根据TAMAKI等[22-23]在STEVENS等[24]、KUWAHARA 等[25]裂纹模型的研究:当第2次加载应力超过第1次加载应力峰值时，岩石才会有大量新微裂纹生成，故在单轴分级加卸载过程中当加载应力低于前一次加载应力时岩石几乎不产生新裂纹，则可以认为单轴分级加卸载各卸载点的弹性能是单轴压缩试验中与各卸载点荷载相等点的弹性能。本次试验拟采用单轴压缩试验、单轴分级加卸载试验和单轴循环加卸载试验3种方式，通过单轴分级加卸载各卸载点的弹性能对单轴压缩过程中能量演化进行分析，利用循环加卸载试验的弹性能演化分析，验证岩石的疲劳损伤和裂纹间的界面摩擦是否对弹性能有影响，以此来验证本文分析方法的正确性及合理性。

1 岩石能量的计算及试验方法

1.1 岩石能量的计算

岩石加载和卸载过程是能量积聚、能量耗散以及能量释放的过程，根据能量守恒定律，假设岩石在加载和卸载过程中不存在热交换，即岩石加卸载过程中能量只以弹性能、耗散能形式存在。试验机对试件所做的功，使岩石原有裂纹闭合、扩展、贯通及新裂纹萌生、扩展和贯通，加载曲线与应变轴围成的面积表示为外部荷载对岩石输入的能量。试验机对岩石做的功一部分能量储存在岩石内部，可以通过试验机卸载方式释放，在一定条件下是可逆的，表现为外力作用下裂纹闭合，外力消失后裂纹张开，卸载曲线与应变轴围成的面积表示释放的弹性能量;另一部分能量在加载过程中耗散，产生不可逆变形，主要表现为外力作用下岩石裂纹扩展、贯通及新裂纹萌生、扩展和贯通，耗散能为加载曲线、卸载曲线及应变轴围成的面积。根据热力学定理:弹性能是可逆的，耗散能是单向不可逆的，其关系[21]为

U=Ud+Ue

(1)

其中，U为外部荷载对岩石试件做功产生的总能量;Ue为储存在岩石内的弹性能;Ud为耗散能。岩石的能量分布如图1所示。

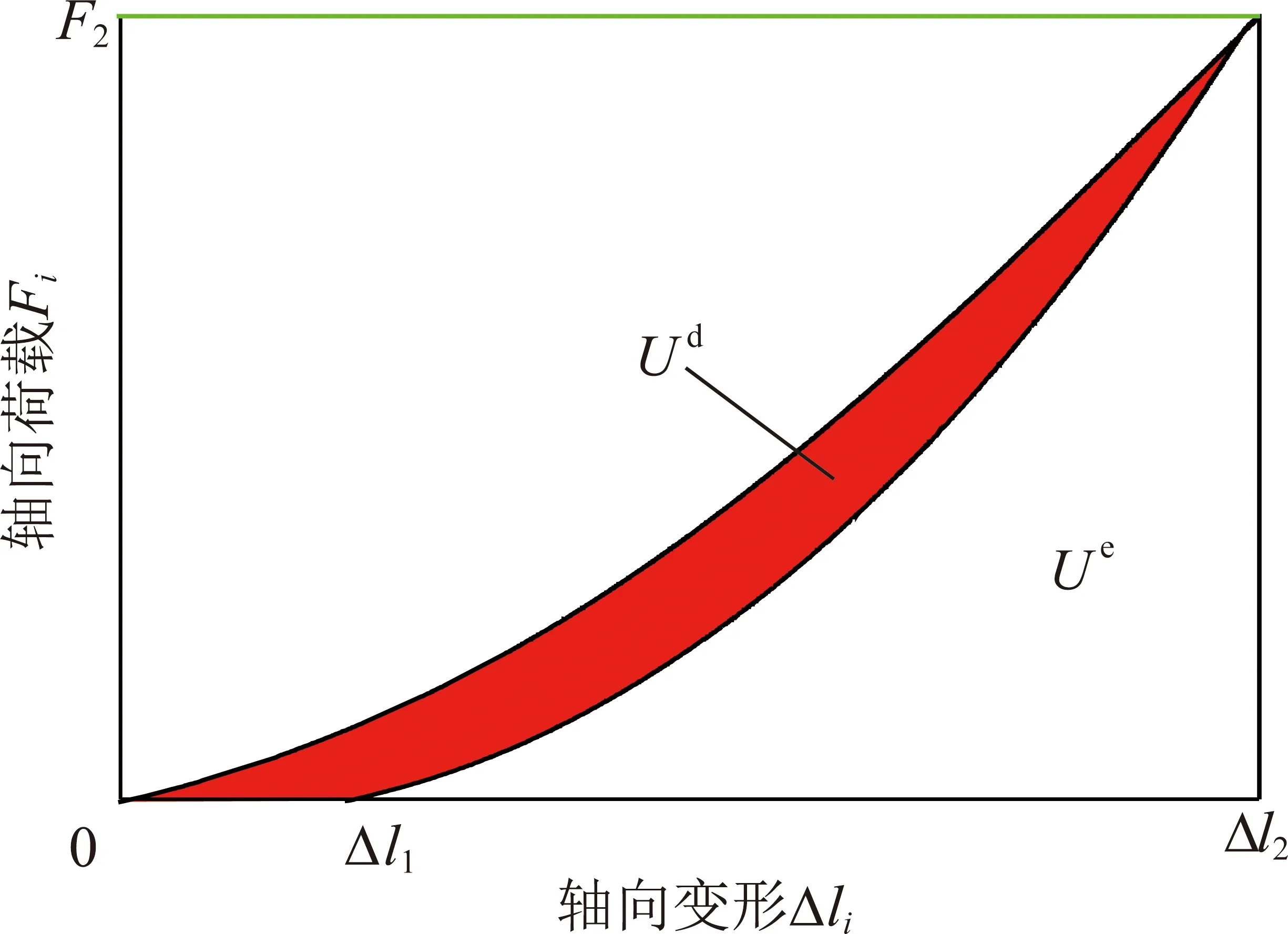
图1 能量示意

图1中卸载曲线下的面积表示弹性能量Ue的大小，加载曲线、卸载曲线和横坐标围成的面积表示岩石的耗散能Ud。能量的具体计算为

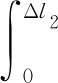
(2)

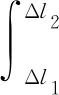
(3)

式中，Δli为轴向变形;Δl1,Δl2分别为轴向荷载为0和F2时的轴向变形;Fi为轴向荷载。

1.2 试验方法

单轴分级加卸载和单轴压缩试验所用的白砂岩取自同一块岩石，内部结构相似、力学性质相近。将白砂岩加工为直径50 mm、高100 mm的标准岩石试件。将圆柱体两端采用砂纸打磨，使其上下表面平行度及侧表面平面度符合国际岩石试验标准试件的要求。单轴压缩试验采用RMT-150B岩石力学测试系统进行试验，以0.5 kN/s速率施加荷载，共7个试件。单轴分级加卸载试验也采用0.5 kN/s的速率进行加载，加载方式0→60→0→80→0→100→0→120→0→140……直至岩石发生破坏。白砂岩单轴分级加载路径图如图2所示。

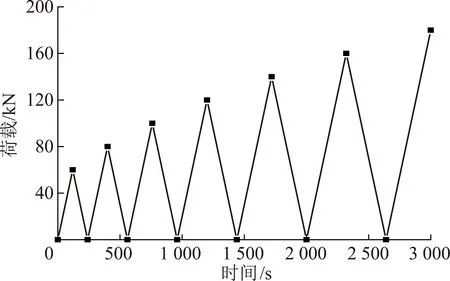
图2 白砂岩加载路径

根据单轴压缩的曲线可知:岩石的压密阶段约在0～60 kN，所以设置初始单轴分级加载的荷载峰值为60 kN后卸载。岩石的单轴抗压强度为163 kN左右，设置以每次循环增加20 kN，能够选择超过6个卸载点。有6个卸载点既能了解岩石各阶段的弹性能，又能够尽量减小分级加卸载的次数，从而减小砂岩的疲劳损伤与裂纹间的界面摩擦对卸载曲线的影响。

2 试验结果分析

图3为单轴压缩试验曲线，由图3可知单轴压缩试验过程可以分为压密阶段、弹性阶段、塑性阶段以及破坏阶段，由于本次加载速率为0.5 kN/s，加载速率较大，故岩石破坏阶段曲线较短。压密阶段的曲线凸向应变轴，弹性阶段为近似直线，试件约在163 kN处发生破坏。单轴压缩在0～60 kN属于岩石的压密阶段，岩石并非通常假设的各向同性体，其内部存在许多的细微裂隙及孔隙，在压密阶段岩石内部的孔隙被压密，轴向荷载-轴向变形曲线随着荷载的增加呈现非线性增长;60～120 kN属于岩石的弹性阶段，在压密阶段岩石内孔隙被压密所以弹性阶段白砂岩的塑性变形相对较少，轴向荷载-轴向变形曲线随着荷载增加呈线性增长;120 kN到白砂岩轴向荷载最大值为白砂岩的塑性阶段，随着荷载增加白砂岩的变形曲线呈非线性增长;单轴压缩达到荷载峰值后试验机开始自动卸荷，此时处于岩石的破坏阶段，由于加载速率为0.5 kN/s相对较大，故破坏阶段不明显。根据热力学原理，在试验机自动卸荷阶段，储存在岩石内的弹性能量开始释放，引起试件的宏观破裂。

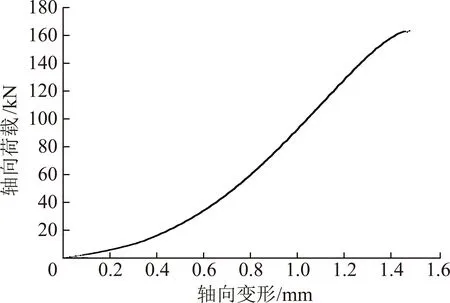
图3 单轴压缩试验曲线

由图4可知，单轴分级加卸载曲线和单轴压缩试验曲线都具有:压密阶段、弹性阶段、塑性阶段和破坏阶段。在白砂岩单轴分级加卸载过程中，当加载的荷载超过前次加载的最大荷载时岩石的加载曲线仍按单轴压缩的曲线规律上升，未受到前几次反复加卸载的影响。虽然岩石存在一定的离散性，但是由于文中单轴压缩试件与单轴分级加卸载试件均取自同一块岩样，离散程度相对较小。通过对比单轴压缩曲线与单轴分级加卸载曲线(图4)，可近似认为单轴压缩曲线是单轴分级加卸各卸载点的外包络线。随着单轴分级加载次数增多，岩石发生疲劳损伤致使岩石在单轴分级加卸载过程中产生了比单轴压缩多的塑性变形，表现为:单轴分级加卸载曲线沿变形轴逐渐向右移动，并且单轴分级加卸载各卸载点随着循环次数增多与单轴压缩曲线逐渐产生了一定程度的偏离。

根据裂纹生成及扩展模型的研究:当单轴分级加卸载的荷载低于前一次加载的最大荷载时，只有较少的裂纹生成和旧裂纹扩展。假设少量裂纹生成和旧裂纹扩展对单轴分级加卸载各卸载点的弹性能无影响，即忽略单轴分级加卸载过程中的疲劳损伤、裂纹间的界面摩擦对弹性能的影响，则可假设单轴分级加卸载的各卸载点的荷载等于单轴压缩试验中的荷载时，各卸载点的弹性能就是单轴压缩中荷载相等点的弹性能。

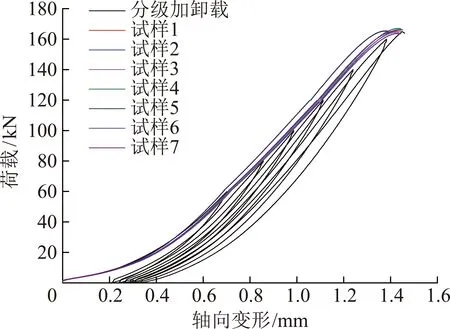
图4 单轴分级加卸载与单轴压缩试验对比曲线

3 单轴压缩试验的能量分析

3.1 滞回效应能演化规律

滞回效应形成的主要原因在于裂纹间的界面摩擦、疲劳损伤以及岩石内部液体的黏滞性[26]。在忽略裂纹间的界面摩擦和疲劳损伤后，单轴分级加卸载的滞回效应能可认为是单轴压缩试验的滞回效应能。在单轴分级加卸载过程中加载曲线与卸载曲线相交形成一个密闭的滞回环，如图5所示BDB围成的面积，滞回环相交处的荷载低于围成滞回环的加载和卸载曲线的荷载最大值。滞回环面积(BDB)就表示单轴压缩过程中的滞回效应能Ucd。由于滞回效应能存在于岩石的加载和卸载过程中，岩石未卸载之前有一部分卸载滞回效应能可以储存在岩石内部，但是这部分滞回效应能不可逆，所以滞回效应能属于特殊的耗散能，既可以存储在岩石内部，又不具有可逆性。基于上述分析岩石的耗散能(ADO围成面积)可以分为滞回效应能(BDB围成的面积)Ucd和塑性耗散能(ABDO围成面积)Udd。

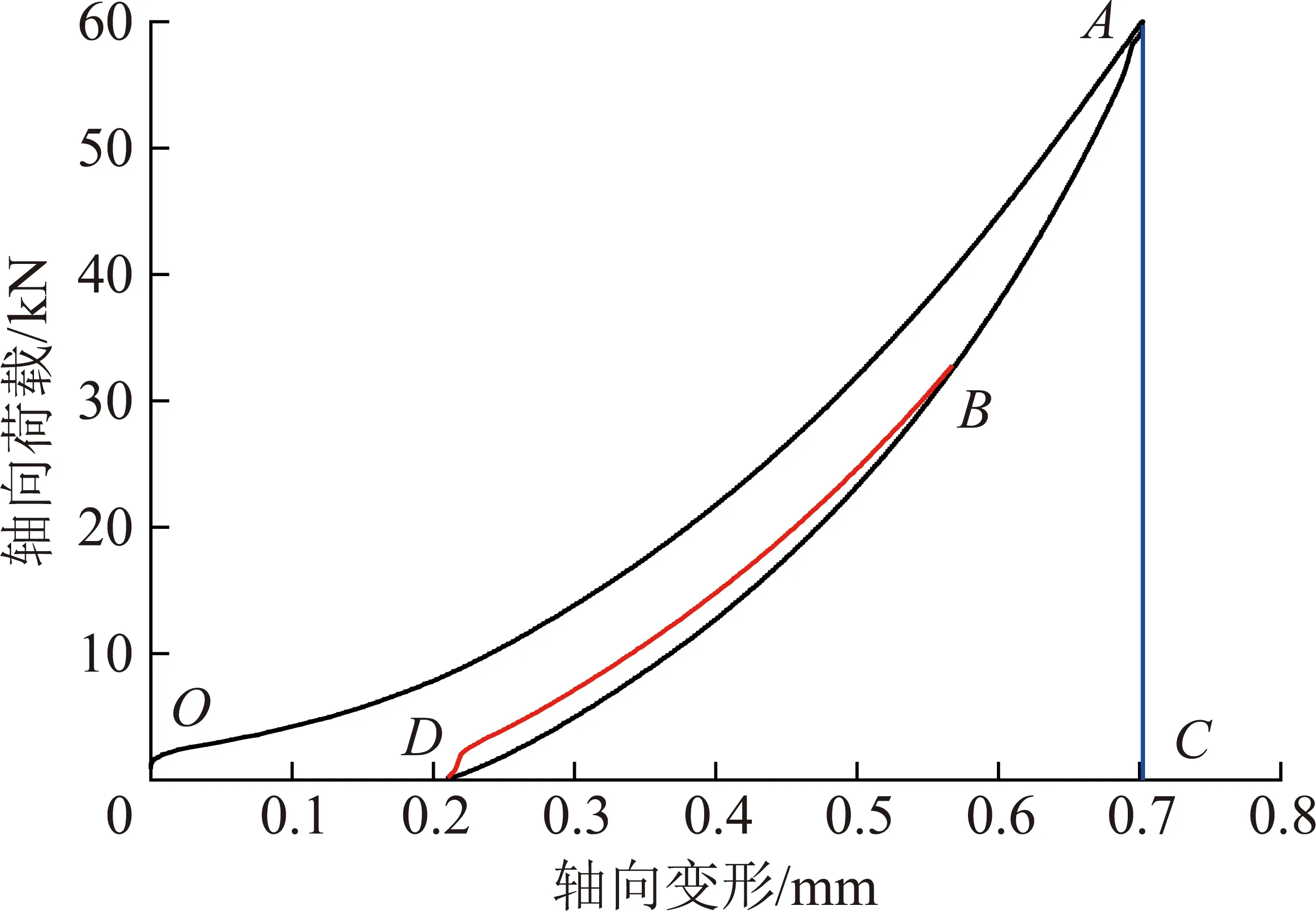
图5 能量示意

根据岩石的能量计算方法可以计算出滞回效应能。基于滞回效应能与荷载关系可以得到关于轴向荷载与滞回效应能的拟合公式，如图6所示。通过上述假设对滞回效应的演化规律进行分析，发现单轴压缩试验过程中的滞回效应能存在于岩石加载的各个阶段，并且随着荷载的增加呈现线性增长，并得到了关于荷载与滞回效应能的拟合公式:

Ucd=0.064 62Fi-3.553 06

(4)

由于文中是忽略加卸载过程中的疲劳损伤和裂纹间的界面摩擦，故可知由岩石内部液体黏滞性引起的滞回效应能呈线性增长。

3.2 单轴压缩试验过程中能量演化

利用上述能量分析、能量的计算方法以及单轴分级加卸载的卸载曲线可以计算出白砂岩单轴压缩试验中与单轴分级加卸载各卸载点对应处的弹性能、塑性耗散能、以及滞回效应能。其具体数值见表1。假设在相同荷载作用下岩石单轴压缩的弹性能与单轴分级加卸载各卸载点的弹性能相等，本次试验的砂岩取自同一块岩石，其内部构造、结构及力学性质相近，本文中各组单轴压缩曲线的能量演化分析都是根据某一试件的单轴分级加卸载曲线进行分析的结果。各组单轴压缩的弹性能分析如图7所示。

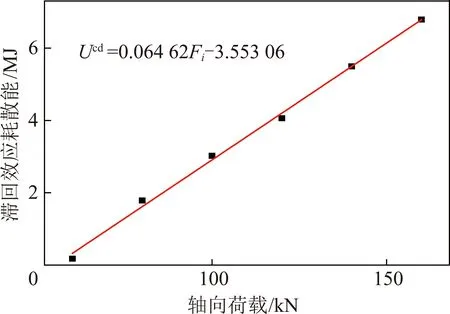
图6 滞回效应能-荷载演化规律

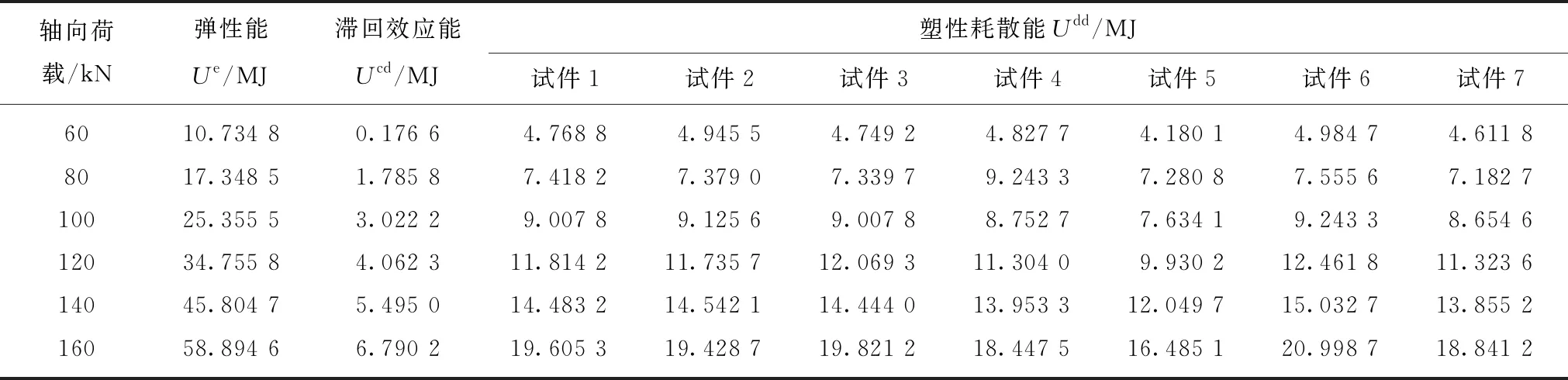
表1 岩石单轴压缩试验下试件能量

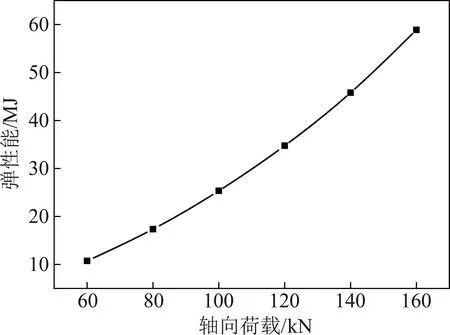
图7 弹性能-轴向荷载

如图7所示,岩石在单轴压缩试验过程中轴向荷载与弹性能量呈同方向近乎线性增长;荷载越大，弹性能越大;随着轴向荷载增大弹性能增长速率也逐渐增大。

基于表1的计算结果可以得出单轴压缩过程中耗散能演化规律，演化规律如图8所示。单轴压缩试验中岩石的压密阶段、弹性阶段也存在塑性变形和塑性耗散能以及滞回效应能。各个试件的塑性耗散能随着荷载的增大整体呈现非线性增长，荷载越大塑性能越大。

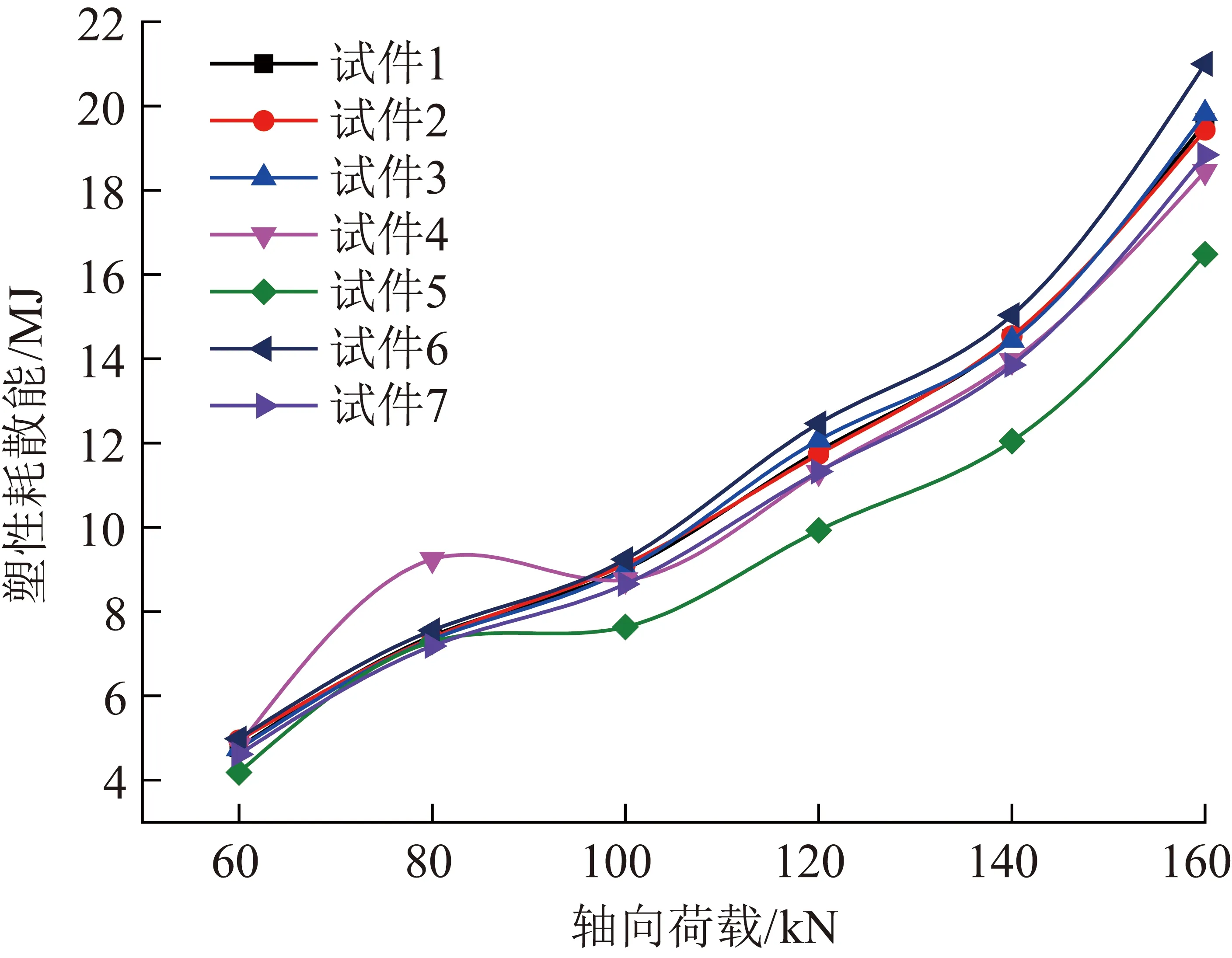
图8 塑性耗散能-轴向荷载

白砂岩的压密阶段与弹性阶段的塑性耗散能的增长速率明显小于岩石临近破坏荷载峰值的塑性能。说明越接近岩石的破坏强度，岩石产生的塑性变形越大，对应的岩石的塑性变形速率增大，需要消耗更多的塑性耗散能。通过上述分析可知弹性能、塑性耗散能以及滞回效应能都随着荷载增大呈现增长趋势。

3.3 单轴压缩试验过程中能量分配

岩石在单轴压缩过程中的能量分配规律的研究，能够进一步对岩石单轴压缩过程中能量演化有更直观的认识，故需要对岩石单轴压缩过程中的能量分配规律进行研究。图9为单轴压缩试验过程中弹性能比例占吸收总能量-荷载曲线图，由图9可知，弹性能量占吸收总能量的比例在0.61以上，试样5的弹性能比例约在140 kN达到最大为0.723。弹性能占吸收总能量比例-荷载曲线呈非线性变化，弹性能所占比例为0.610～0.723。在80 kN左右弹性能比例最小。

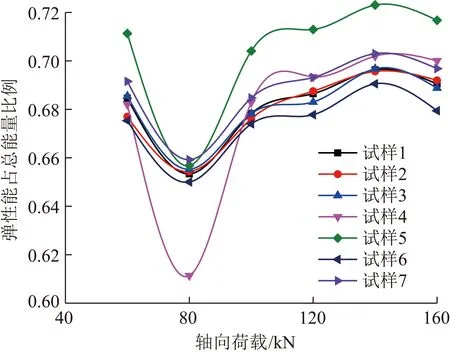
图9 弹性能比例-荷载曲线

图10为单轴压缩试验过程中塑性耗散能占吸收总能量比例-轴向荷载的曲线图，由图10可知，塑性耗散能在单轴压缩过程中占总吸收能量的0.190～0.325，塑性耗散能占总吸收能量比例-荷载曲线呈非线性变化，当荷载约在60 kN时试件6与试件5的塑性耗散能占吸收总能量的比例相差0.38。在压密阶段塑性耗散能比例大于其他阶段的塑性耗散能，主要原因是岩石并非通常假设的均质体，其内部存在大量的孔隙，在压密阶段岩石的孔隙被压密，产生了一定的不可逆变形，对应的塑性能相对较大。在岩石的压密阶段、弹性阶段以及塑性阶段的前期随着荷载的增加塑性耗散能占总能量的比例逐渐减小，在塑性阶段后期即临近破坏时，岩石的塑性耗散能比例呈增大趋势。

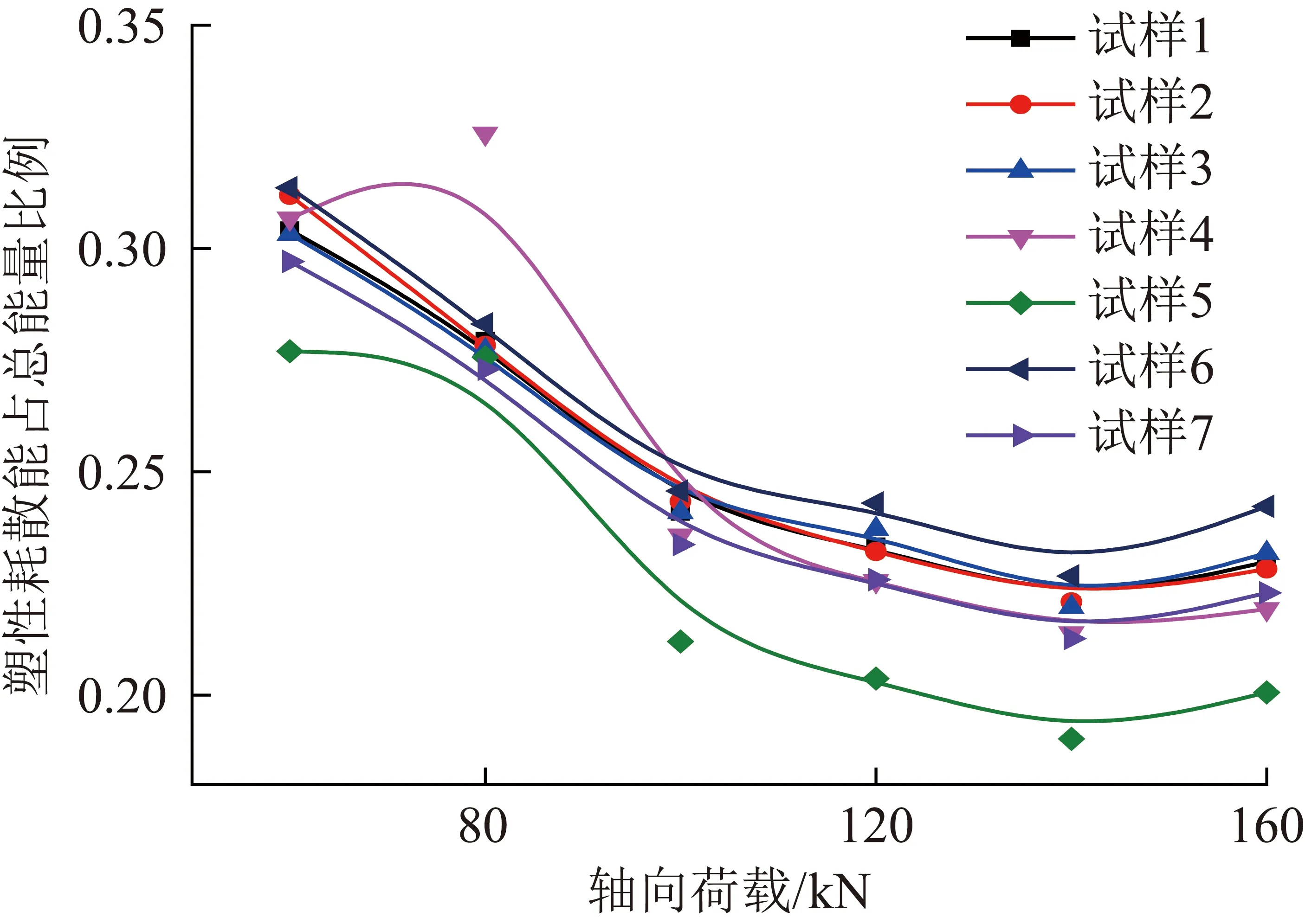
图10 塑性能比例-荷载演化

3.4 弹性能与耗散能比值分析

弹性能与耗散能作为岩石在加卸载过程中的两种能量形式，两者的能量比值分析有助于理解岩石在单轴压缩过程中弹性能与耗散能的增长速率的比较。弹性能和耗散能在单轴压缩过程中虽然都是整体呈非线性增长，但是两者在单轴压缩过程中增长速率的对比需要展开进一步研究。当弹性能与耗散能比值增长时说明弹性能增长速率大于耗散能增长速率，反之则耗散能增长速率高于弹性能增长速率。在岩石60～80 kN处的弹性能虽然增长，但是其增长速率低于耗散能的增长速率;荷载处于80～140 kN时弹性能增长速率高于耗散能增长速率;在140～160 kN处岩石的耗散能增长速率高于弹性能增长速率。

岩石在压密阶段由于岩石孔隙和微裂纹被压密，所以在压密阶段由于产生了较大耗散能，弹性阶段也存在耗散能，一般而言岩石的弹性能与耗散能最大比值在岩石的塑性阶段。弹性能量指数作为岩石的储能性指标以及预测岩石发生岩爆倾向性指标，定义为岩石加载至其单轴压缩试验峰值强度80%左右处卸载，加卸载过程中弹性能与耗散能比值为弹性能量指数WET。其计算公式为

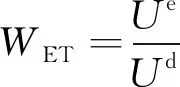
(5)

当WET≥5时有强岩爆倾向;当WET在2～4.99时有中岩爆倾向;当WET<2时有弱岩爆倾向。该指标很好地表征了岩石破坏前贮存弹性能的能力，可以较好地表明岩爆的可能性。

基于上述分析，对砂岩单轴压缩试验过程中的弹性能与耗散能比值进行研究，如图11所示。单轴压缩试验中弹性能与耗散能比值随着荷载增长呈非线性变化，接近破坏荷载时岩石的变形急剧增大，砂岩产生了较大的不可逆变形，所以在接近破坏应力时岩石的弹性能与耗散能比值减小，并且弹性能与耗散能比值在外部荷载是砂岩强度的80%时达到最大，即本次研究的弹性能与耗散能最大比值是岩石弹性能量指数，从而验证了本文分析方法中关于能量的演化趋势具有一定的合理性，但是文中假设的精确性和正确性需要进一步来验证。

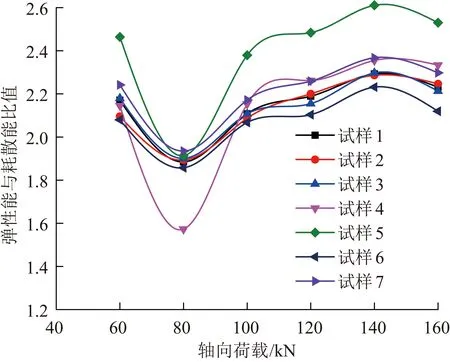
图11 弹性能与耗散能比值演化

4 分析方法的验证

关于单轴压缩试验过程中能量的实时演化分析是基于忽略加卸载过程中的疲劳损伤和裂纹间的界面摩擦对弹性能的影响。但是对于这一假设的正确性需要进行单轴循环加卸载试验进行验证。按照2.2节试验方法中试件要求将红砂岩制成高100 mm，直径50 mm的标准岩石试件，使用与白砂岩相同的加载速率对红砂岩试件进行单轴循环加卸载试验，每组单轴循环加载的循环上限幅值分别为10，20，30，40，50，60，70，80，90 kN，循环下限幅值为0，每组试件分别进行50次循环加载无论试件是否破坏，都不再进行加载。循环加载的曲线如图12所示。

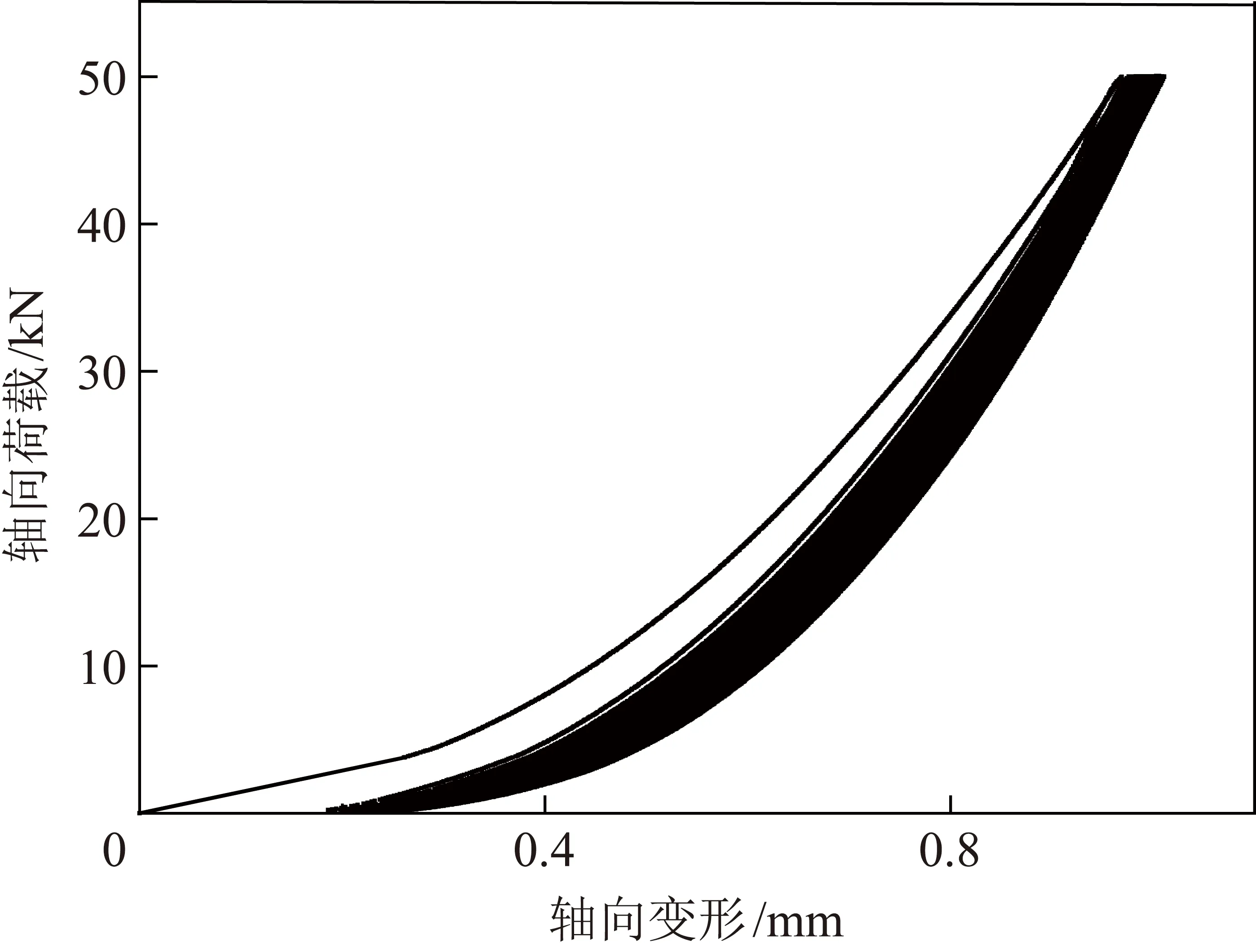
图12 第5组单轴循环加载曲线

岩石并非通常假设的各向同性体，其内部存在许多细微裂纹，裂纹的相邻界面间的接触面也并非光滑，随着循环次数增多，岩石的疲劳损伤和裂纹间的界面摩擦会使岩石产生新的塑性变形，并且随着循环次数的增多循环加载曲线逐渐右移。图13为单轴循环加卸载试验的弹性能演化规律。由图13可知,随着循环次数的增多红砂岩的弹性能变化幅度较小，是可以忽略不计的。因此可以认为单轴循环加卸载作用过程中的疲劳损伤和裂纹间的界面摩擦对岩石的弹性能无影响。通过对不同荷载峰值下单轴循环加卸载的弹性能演化规律的研究，可以证明文中假设的正确性与精确性。

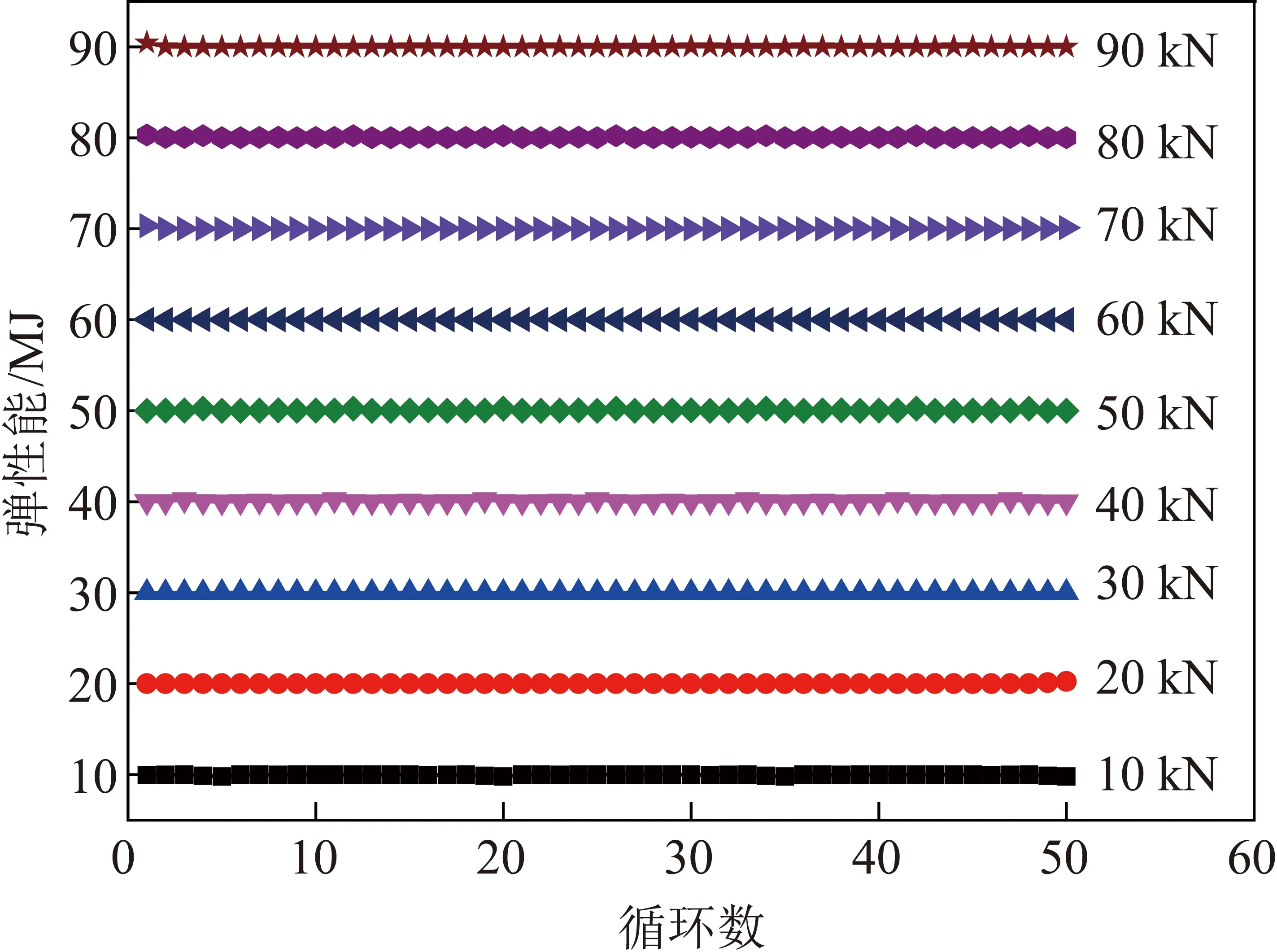
图13 弹性能演化规律

5 结 论

(1)岩石单轴压缩试验曲线与单轴分级加卸载曲线同样具有压密阶段、弹性阶段、塑性阶段和破坏阶段，各个阶段始终都存在弹性能、塑性耗散能以及滞回效应能，并且都随着荷载增大而增大。

(2)滞回效应能存在于岩石的加载和卸载阶段，可以储存在岩石内部，但是是一种不可逆的特殊耗散能，且滞回效应能随着荷载增大呈线性增长。

(3)在单轴压缩试验中弹性能占总吸收能量0.610～0.723，塑性耗散能占吸收总能量的0.190～0.325;在60～80 kN处弹性能增长速率小于耗散能增长速率，在80～140 kN处弹性能增长速率高于耗散能增长速率，在140～160 kN处弹性能增长速率小于耗散能增长速率，并且在白砂岩强度的80%左右处的弹性能与耗散能比值达到最大，与弹性能量指数相等，说明了该分析方法具有一定的合理性。

(4)单轴循环加卸载试验中反复加卸载产生的疲劳损伤和裂纹间的界面摩擦产生新的塑性变形主要表现为使加卸载曲线逐渐右移，但是对弹性能无影响，从而验证了单轴分级加卸载各卸载点的弹性能是单轴压缩试验对应点的弹性能这一假设的正确性与精确性。

(5)利用单轴分级加卸载各卸载点的弹性能对单轴压缩试验中能量演化规律进行分析，为单轴压缩试验中能量演化研究提供了新的方法。