基于一次二阶矩法渡槽系统模糊可靠度分析

祝彦知 尚峰 纠永志

摘 要：为了更合理地评价钢筋混凝土渡槽结构在正常使用极限状态下的安全可靠性，针对在役钢筋混凝土渡槽结构，考虑影响其结构稳定性因素的随机性及模糊性，基于一次二阶矩法建立了渡槽结构底板與侧墙抗裂随机模糊可靠度模型，编制了相应的程序，并利用PNET法针对某工程实例进行了系统模糊可靠度分析。结果表明：在相同条件下，中心点法和验算点法可靠性指标计算结果与建立的模糊可靠度方法基本一致，验证了模糊可靠度方法的正确性;在不同条件下，渡槽系统可靠性指标随着考虑相关变量因素的增多而减小，这与实际情况相符，即考虑变量的随机性与模糊性更接近于结构真实情况，所得解更为合理;传统可靠度计算方法所得抗裂能力可靠性指标结果偏大，高估了渡槽结构整体的可靠性，采用传统方法得到的极限状态设计值偏于不安全，实际工程中应考虑影响因素的随机模糊性。

关键词：系统模糊可靠度;一次二阶矩法;正常使用极限状态;钢筋混凝土渡槽;PNET法

中图分类号：TV331文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.06.025

Fuzzy Reliability Analysis of Aqueduct System Based on First Order Second Moment Method

ZHU Yanzhi1，2， SHANG Feng1，2， JIU Yongzhi1，2

（1.School of Civil Engineering， Zhongyuan Univercity of Technology， Zhengzhou 450007， China;

2.Architectural Design and Research Institute， Zhongyuan University of Technology， Zhengzhou 450007， China）

Abstract：In order to evaluate the safety and reliability of reinforced concrete aqueduct under the limit state of normal use more reasonably， this paper established the fuzzy random anti-cracking of the floor and side wall of the aqueduct structure based on the first-order second-moment method， considering the randomness and fuzziness of the factors affecting the structural stability of the existing reinforced concrete aqueduct structure. The reliability model and the corresponding program were compiled， and the fuzzy reliability of the system was measured by the PNET method. The results need to show that under the same conditions， the reliability indices of the center point method and the checking point method are basically the same as those of the present method， which verifies the correctness of the proposed method. The randomness and fuzziness are closer to the real situation of the structure， and the solution is more economical. The reliability index of crack resistance obtained by traditional reliability calculation method is too large， which overestimates the reliability of aqueduct structure. The design value of the limit state obtained by the traditional method is unsafe. The random fuzziness of influencing factors should be examined in practical engineering.

Key words： system fuzzy reliability; first-order second moment method; normal service limit state; reinforced concrete aqueduct; probabilistic network evaluation technique

近年来国内外对结构可靠度研究相当活跃，从理论到实践都有了长足发展，我国部分结构设计规范如《水工混凝土结构设计规范》（SL 191—2008）就是基于可靠度理论方法制定的，该规范将荷载效应S与结构抗力R的平均值和标准差代入已有的概率密度分布函数中，对结构进行线性化处理，提出了结构的失效概率或可靠性指标。目前大部分可靠度计算是针对单个构件或构件的一个截面的单一失效模式而言的，然而在工程实践中各种建筑物是由多种构件组成的结构体系。我国渡槽工程多建设于20世纪50年代，大多数钢筋混凝土渡槽仍在继续运行，而影响渡槽结构体系正常使用的安全稳定性因素大多是模糊和随机的，因此研究在役钢筋混凝土渡槽的系统随机模糊可靠度非常重要。

国内外学者针对渡槽安全稳定性分析常用的方法有理论规范法、经验算式法、有限元数值分析法。Suarez等[1]结合阿尔罕布拉渡槽历史和材料的特殊性对其进行了几何建模，分析了渡槽的失穩风险，建议加固拱圈的厚度。胡炜[2]对水利工程结构中常见的堤坝、渡槽、水闸等结构的可靠度理论研究现状进行了总结和展望。夏富洲等[3]依据新老水工混凝土结构设计规范，计算了渡槽抗裂可靠度，并分析了荷载和混凝土的变异性对抗裂可靠度的影响，但忽略了影响因素的随机性与模糊性。段成晓等[4]把渡槽结构层间位移及顶点位移作为失稳控制标准，通过Monte-Carlo模拟与有限元法相结合，对渡槽结构位移的可靠度进行了分析。解伟等[5]针对涵洞式渡槽每个构件建立了相对应的功能性函数，利用结构之间的关联性，计算了渡槽的系统可靠度，但未考虑影响因素的随机模糊性。雷杰[6]采用响应面法针对南水北调工程中某预应力渡槽，分析了其结构的可靠性指标。王盛[7]以梁式渡槽为研究对象，针对不同失效模式建立相对应的功能性函数，利用失效模式之间的相互性，计算出了渡槽结构的系统可靠性指标。Huang等[8]针对尼勒克沟渡槽，运用反应谱分析法计算了其频率和振型，得出了渡槽在水平地震作用下的可靠度。Hohenbichler等[9]针对结构可靠度计算中存在多个变量时与结构实际情况的偏差，提出了更好的解决方案。以上渡槽结构可靠度分析方法均是针对渡槽承载力极限状态下的确定性分析，大多是针对一个构件或构件的单个截面的单一失效而言的，未考虑变量的随机模糊性，而在役渡槽在运行期间受到各种荷载、环境等复杂因素的影响，其承载力和安全可靠性会逐步降低，这些复杂因素大多是模糊和随机的。因此，针对在役渡槽应侧重正常使用极限状态下的可靠度分析，应将各种相关因素视为随机变量，运用模糊数学理论及概率统计方法来分析其系统随机模糊可靠度。

本文考虑引起渡槽结构安全稳定性降低因素的随机模糊性，结合渡槽结构体系，基于一次二阶矩法对某在役钢筋混凝土渡槽结构进行了随机模糊可靠度分析。

1 模糊可靠度模型的建立

1.1 承载力极限状态下的可靠度模型

结构的极限状态本质上是结构工作状态的一个阈值，如果超过这个阈值，则结构处于不稳定、不安全、不耐久的状态;若没有超过这一阈值，则结构处于稳定、安全、耐久的状态[10]。目前一般采用中心点法或验算点法（JC法）来计算结构承载力极限状态下的可靠度。如果用X1、X2、…、Xn表示结构的基本随机变量，用R表示结构抗力，用S表示荷载效应，则结构的功能函数为

Z=g（X1，X2，…，Xn）（1）

或

Z=g（R，S）=R-S（2）

Z=R-S=0称为结构极限状态方程，当Z>0时结构处于安全稳定状态，Z=0时结构处于极限状态，Z<0时结构处于失效状态。

若R与S彼此相互独立，当R与S均服从正态分布时，其平均值和标准差分别为μR、μS和σR、σS，Z也服从正态分布，则结构抗裂可靠性指标为

β=μZσZ=μR-μSσ2R+σ2S（3）

式中：μZ、σZ分别为功能函数的平均值和标准差。

若R与S均服从对数正态分布时，则Z=ln R-ln S且也服从正态分布，有：

β=μZσZ=μln R-μln Sσ2ln R+σ2ln S（4）

式中：μ、σ为均值和标准差，下标表示其在不同分布状态下。

1.2 正常使用极限状态下的可靠度模型

正常运用时影响结构抗力的随机模糊因素包括结构几何参数、材料性能、分析模型，以及试件的结构抗力试验值与实际抗力之间的不确定性。影响荷载效应的随机模糊因素主要是荷载自身的不确定性。

对于材料单一的结构：

KR=RRK=KZKPKMKa（5）

式中：KR为构件性能值;RK为规范规定的材料性能和几何参数标准值;KZ为结构抗力与试验值之间的不确定性附加变量;KP为构件结构抗力计算不确定性附加变量;KM为构件材料性能的不确定性附加变量;Ka为构件几何参数的不确定性附加变量。

对于复合性材料结构：

R=KZKPRP=KZKPR（fi，ai）（6）

式中：RP为计算构件抗力值;fi为构件第i种材料性能参数;ai为第i种材料的几何参数。

不同结构构件荷载效应模型并不相同，本文以槽身为简支梁结构的矩形钢筋混凝土渡槽为例，其荷载效应为

S=18（q1+q2）l2（7）

式中：q1、q2为随机变量;l为定值，视不同结构取相应值。

1.3 模糊可靠度模型

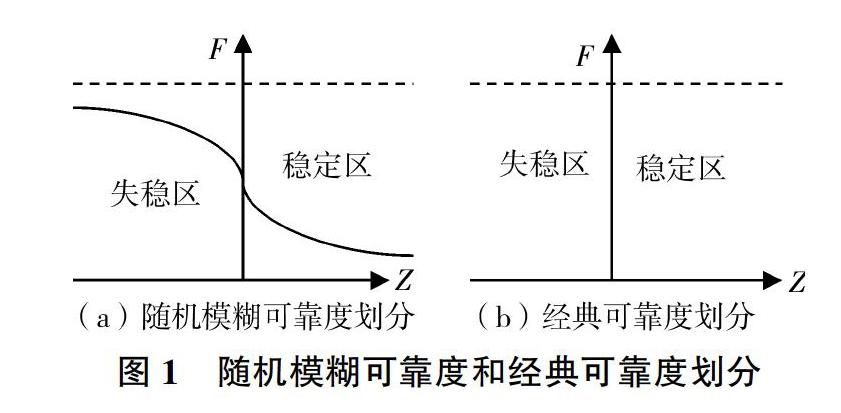
结构在正常使用极限状态下，结构抗力R及荷载效应S不仅具有随机性，而且具有模糊性，所以正常使用极限状态下的方程Z也是随机、模糊的。式（2）没有明确的区域和边界，而是存在一个可以允许的过渡区间，如图1所示，它的模糊集为μA（Z），也称为Z的隶属度函数。

假设钢筋混凝土渡槽结构在正常使用极限状态下Z的概率密度函数服从正态分布，即

f（Z）=12πσZexp[-（Z-μZ）22σ2Z]（8）

式中：Z为结构在正常使用极限状态下的抗裂能力;μZ为结构在正常使用极限状态下的抗裂均值;σZ为结构在正常使用极限状态下的抗裂标准差。

依据模糊数学理论，钢筋混凝土渡槽结构在正常使用极限状态下开裂失效是一个随机模糊事件，记其失效事件为A，则其发生的概率为

p（A）=∫+SymboleB@

-SymboleB@

f（Z）μA（Z）dZ（9）

其模糊可靠性指标为