基于人工神经网络的边坡新多点监控模型

余晓露 郑东健

摘 要：以邊坡监测数据建模是掌握边坡安全状况的主要途径，目前多数边坡模型都是单测点模型，未考虑点间相互关系，不能充分反映整个边坡的状况。基于此，构建人工神经网络多点模型，以其在解决非线性问题上的优势，寻找空间坐标与测点变形的对应关系，并由模型输出的位移值计算边坡体体积变化，对体积变化值和单测点位移值分别建立常规回归模型，进行比较，结合具体工程分析表明，所建多点模型能较好反映边坡整体变形状况。

关键词：神经网络;边坡;多点监控模型;体积变化

中图分类号：TV737文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.06.023

A New Multi-Point Monitoring Model of Slope Based on Artificial Neural Network

YU Xiaolu1， ZHENG Dongjian1，2，3

（1.College of Water Conservancy & Hydropower Engineering，Hohai University， Nanjing 200098， China; 2.State Key Laboratory of

Hydrology-Water Resources & Hydraulic Engineering， Hohai University， Nanjing 210098， China; 3.National Engineering Research

Center of Water Resources Efficient Utilization & Engineering Safety， Hohai University， Nanjing 210098， China）

Abstract： Displacement is the most intuitive form of slope failure， so modeling with the monitoring data is the main method to master the safety of slopes. Most of the models are analyzed by single measuring point. They ignore the interconnections between points and cannot reflect the deformation of the whole slope. This paper constructed a multi-point model of neural network， found the relationship between spatial coordinates and deformation of points and converted the model output to the volume. Then， it established conventional regression models for volume and displacement of single point. Taking a specific project as an example， the multi-point model is better than single point in reflecting the whole slope， which has certain reference value for similar projects.

Key words： neural network; slope; multi-point monitoring model; volume change

建立边坡监控模型，实时分析边坡变形状况及发展趋势，对预防及减少滑坡等灾害的发生意义重大。边坡变形监控建模方法大体可分为有限元数值仿真法和实测数据建模两大类。边坡岩土体构造复杂，具有非均质性及各向异性，且岩土体参数高度非线性，通常有限元法难以实施[1-2]。相较而言，获取边坡实测数据更易实现，故工程中大多采用实测资料建模的监控方法。如：易庆林等[3]基于BP神经网络，建立了库区滑坡的单点变形预测模型;孙世国等[4]基于灰色理论，建立了改进的边坡单点灰色模型;黄丽等[5]建立了基于降雨和水位作用的滑坡时序模型。以上模型都是单点模型，将测点孤立于整体，忽略了点间关联性，所得分析结果不能确切反映边坡整体变形。有学者指出[6]，建筑物中各点变形相互影响，建模过程中应考虑这种空间关联，构建综合模型。何习平等[7]建立边坡加权多点灰色模型，将传统灰色模型扩展为M-GM（1，1）模型，实践证明其短期预测精度高于传统单点模型。黄铭等[8]建立了基于径向基函数神经网络的边坡多点监控模型，实践表明预测结果能较好反映位移的变化趋势。这些研究中多点模型最终仍以单测点变形为输出，并没有提出能反映边坡变形的综合评价指标。基于此，笔者提出一种新的边坡多点监控模型思想，构建多点神经网络模型，实现边坡点内插，有效解决了位移空间分布函数难以确定的问题，由点及体，提出以边坡体体积变化来衡量边坡变形，实现了实际意义上的多点监控，最后以某水电站高边坡为例进行了计算验证。

1 多点监控模型的构建

1.1 建模基本思路

资料表明，当边坡自身未产生裂缝时，距离相近的测点之间不存在位移突变，可认为两点变形具有某种关联性，距离越近关联性越强[9]。目前的单点模型正是忽略这种点间关联，故预测结果不具有代表性。

常规单点模型考虑水位、温度、时效等因素对测点变形的影响。相比而言，多点模型在此基础上引入点的空间坐标及位移值，多点模型可简化如下：

ym=f（H，T，θ，di，δi，dm） i∈（1，2，…，n）

式中：ym、dm分别为预测点m的位移值及坐标值;H、T、θ分别为水位、温度、时效影响因子;di、δi分别为各已知测点的坐标值及位移值;n为已知测点总数。

边坡变形受诸多因素影响，采用人工神经网络算法建立多点模型，能较好处理非线性映射问题。上文多点简化模型，当环境因素、已知测点的坐标及变形、预测点的坐标及部分变形值已知时，可模拟点间关系，实现对预测点后期的变形预测。而本文要构建以体积变化值为综合衡量指标的多点模型，为实现体积的高精度计算，需对目标边坡体内插求未知点变形。由于内插点为全新点，前期无监测数据，因此理想的多点模型无法实现。当点间关系难以发掘时，不妨将分离相关关系转化成相关关系的统一表达。边坡体体积变化值是各测点变形值的综合表达，其中包含了各测点的联系，只需寻找空间坐标与测点变形的对应关系即可。

1.2 模型构建步骤

（1）人工神经网络模型内插边坡点位移。①由已知数据确定参与建模的各测点。为保证建模效果，选择分布相对集中的测点。对建模测点监测数据的完整性及合理性进行分析，必要时进行数据填充及纠正。②由建模测点确定目标边坡体空间范围。建模测点横纵坐标的最大、最小值构成边坡体的水平投影范围，边坡体基底坐标取建模测点中纵坐标最小值。建基面与边坡坡面所夹的处于水平投影内的部分即目标边坡体。③设置内插点。由建模测点在边坡体上的分布情况确定合适内插点，将边坡划分为若干块体以便计算体积。其中内插尽量保证各点分布均匀，能更好反映边坡地形。④建立人工神经网络模型，预测内插点的变形。以多点空间坐标为输入，变形为输出，δi=f（xi，yi，zi），其中δi为某点i的变形值，xi、yi、zi分别为i点的三向坐标值。

（2）单点变形向边坡体体积转化。在CAD中输入各测点三维坐标，将已知测点与内插点相互连接，曲面近似拟合边坡面，即可绘制出目标边坡体三维实体图，由查询属性功能，一键获取目标边坡体体积，与变形初始时体积相减即得体积变化值。

（3）多点模型与单点模型对比分析。边坡单点变形与水位、温度、时效因素有关，所得一系列体积变化值也与之相关，根据体积变化值和单点变形值分别建立回归模型，并进行比较。

1.3 人工神经网络模型的选取及参数设置

在建立多点模型进行边坡内插时，优先选择BP神经网络算法。该算法由样本正向传播及误差逆向传播两步来实现，在误差逆向传播过程中通过不断调整网络的权值和阈值，实现输出符合设定误差的结果。

BP神经网络模型主要由输入层、隐含层、输出层构成。要预测的目标为输出层，目标的影响因素为输入层，通常影响因素不止一个。有实例表明[10]，含一个隐含层的3层神经网络结构，可无限逼近任意非线性函数关系，故建模时通常采用3层BP神经网络结构。模型的输入与输出节点数由输入、输出变量确定，隐含层节点数可由经验式（1）～式（3）初步确定取值范围，然后通过试算最终确定。

m=n+l+α（1）

m=lb n（2）

m=nl（3）

式中：m、n、l分别为隐含层、输入层、输出层节点数;α为1～10之间的常数。

由已知数据确定模型的结构与输入层、输出层、隐含层节点数。选择恰当的训练函数及层间传递函数，设置训练步数、学习速率、目标误差等网络参数。当建模测点数较少时，为避免模型过拟合，需按一定比例划分训练样本、验证样本和测试样本。

2 工程实例

2.1 工程概况

某电站高边坡位于枢纽右岸坝肩下游侧，顺河向长约300 m，自1997年上坝公路开挖施工后，边坡出现较大范围的坍塌、滑动，每逢雨季还会发生土体塌滑现象。该高边坡监测系统由环境量监测、表面位移监测、深层位移监测及地下水监测组成，其中边坡表面位移监测系统布置了tp01～tp07、tpn1～tpn8共15个测点。

2.2 模型建立与结果分析

2.2.1 BP神经网络模型建立

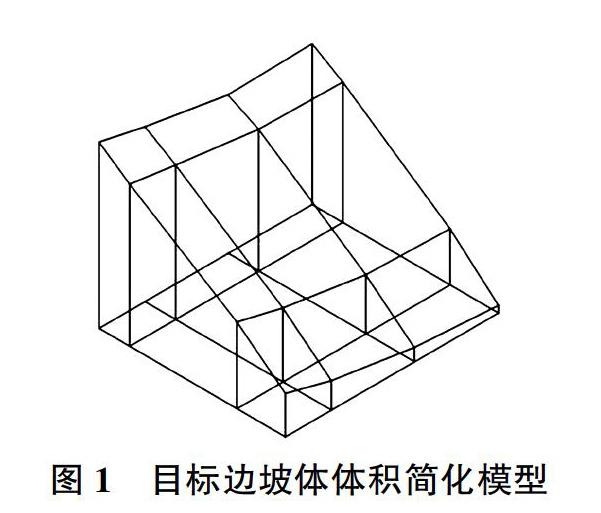
选择监测数据完整、数值可靠且位置相对集中的tpn1、tpn4～tpn8这6个表面位移测点来建立多点模型，由这6个建模测点的平面坐标确定目标边坡体的平面范围为x∈（17.566 1，89.080 1）、y∈（109.688 1，191.475 7），目标边坡体底高程为200 m。以内插尽量均匀合理分布为原则，共内插12个测点，将目标边坡体划分为9块，近似求其体积，体积简化模型见图1。

目标测点有2011年1月—2016年12月共69期位移监测数据，用每个时期数据建模，可得一个体积值，由此可得到2011—2016年边坡体体积变化值。这里以2011年1月数据为例进行建模分析。

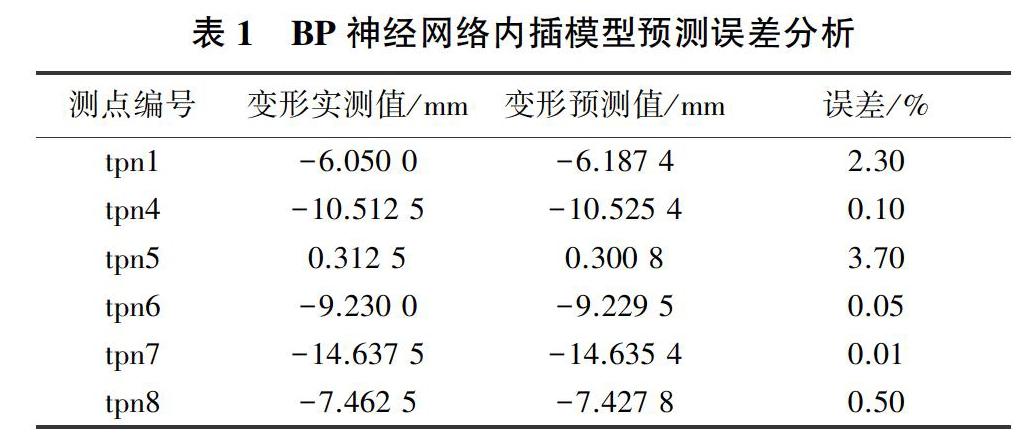
本文选择3层BP网络，以測点坐标为输入、测点竖向变形为输出，则输入层、输出层节点数分别为3、1，由经验公式确定隐含层节点数m∈（2，5）（隐含层数不能超过样本数），代入网络试算，最后取3，即建立3层BP（3，3，1）模型。网络权值及阈值随机产生，设置本次训练迭代次数为1 000，目标误差设置为0.2。训练函数选择trainlm。其中建模样本数为6，按4/6、1/6、1/6的比例划分训练样本、验证样本和测试样本。通过模型多次随机组合，挑选出符合目标误差的最佳模型。由2011年1月数据所建模型，在随机组合试算358次后，输出误差为0.178，符合目标误差要求，即可用此时训练好的网络进行预测。将模型预测的已知测点位移值与实测值比较（见表1），可见模型预测值与实测值相差不大，最大误差不高于5%，表明模型预测精度较高，用此模型进行边坡内插较为可靠。

2.2.2 回归模型的建立及对比分析

通过建立的神经网络模型进行内插计算，最终求得边坡体一系列体积变化值。任意选择一建模测点（本文随机选取tpn1），用边坡体积变化值及单测点tpn1的变形值δ分别建立回归模型进行比较。

δ=δH+δT+δt

式中：δH、δT、δt分别为水压分量、温度分量、时效分量。

绘制体积变化及tpn1测点变形的实测值及拟合值过程线，见图2、图3。目标边坡体体积变化过程线复相关系数为0.82，拟合精度较高，水压分量及温度分量所占比例较小，时效分量占比为80%以上，边坡体积呈明显周期性变化规律，在0～20 m3范围上下波动，逐渐趋于稳定。tpn1测点垂向位移过程线复相关系数仅为0.46，模型拟合精度较差。

对比回归模型，当单点数据部分缺失或者数据测量有误时，单点模型拟合效果较差，用单点模型来预测边坡整体的发展趋势不可行，而由多点变形计算出的体积指标可以减少单点数据误差对整体模型的影响，模型精度较高。

绘制体积变化过程线及参与建模的6个测点的位移过程线（见图4），可看出各测点位移过程线整体变化趋势一致，这恰好验证了点间变形具有一定相关性。其中体积变化过程线呈明显周期性变化趋势，且变化趋于稳定，与边坡实际变化规律相符，而这些信息从单点位移过程线无法得到。这表明多点模型比单点模型能更好地反映边坡实际变形状况。

3 结 语

（1）构建了基于BP神经网络的边坡多点模型，并提出以边坡体体积变化作为综合评价指标，将该模型应用于具体边坡工程中，所得结果与单点模型相比精度更高，更能反映边坡实际状况，多点模型切实可行。

（2）BP神经网络算法的精度与样本数量有一定关系，当已知测点过少时如何建立多点模型还有待研究。

（3）本文构建的多点模型最终以边坡体体积作为衡量指标，是多点多方向位移值在空间上的综合表达，如何将这种空间表达与传统单测点时间维度上的预测模型相结合，需进一步研究。

参考文献：

[1] 罗凌晖，周建，蔡露，等.各向异性成层边坡的稳定性分析[J].中南大学学报（自然科学版），2019，50（8）：1883-1890.

[2] 郑东健，顾冲时，吴中如.边坡变形的多因素时变预测模型[J].岩石力学与工程学报，2005，24（17）：3181-3184.

[3] 易庆林，曾怀恩，黄海峰.利用BP神经网络进行水库滑坡变形预测[J].水文地质工程地质，2013，40（1）：124-128.

[4] 孙世国，王超.基于改进灰色模型的边坡位移预测[J].黑龙江科技大学学报，2017，27（1）：60-63.

[5] 黄丽，罗文强，李飞翱，等.基于诱发因素作用特征的滑坡变形时序模型[J].长江科学院院报，2015，32（10）：28-32.

[6] 王穗辉，潘国荣.基于MATLAB多变量灰色模型及其在变形预测中的应用[J].土木工程学报，2005，38（5）：24-27.

[7] 何习平，华锡生，何秀凤.加权多点灰色模型在高边坡变形预测中的应用[J].岩土力学，2007，28（6）：1187-1191.

[8] 黄铭，闫彭彭，刘俊.降雨及时效影响下高边坡复杂位移多点神经网络监控模型[J].工业建筑，2016，46（9）：99-102.

[9] 季威，劉晓青，林潮宁，等.基于BP神经网络的大坝新多测点位移模型[J].水利水电技术，2019，50（2）：112-117.

[10] AOKI K， KANEZASHI M， MAEDA C. Learning Algorithm for Neural Networks by Solving Nonlinear E-quations[C]//Proc.of ANNPS.Yokohama：IEEE，1993：461-466.

【责任编辑 张华岩】