利用大数据挖掘矿石中主要矿物之间的关系

2020-10-12陈军林彭润民

岩石矿物学杂志 2020年5期

陈军林，闫岩，彭润民

(中国地质大学 (北京) 地球科学与资源学院，北京 100083)

随着地学数据的不断积累，地质学进入了大数据时代。大数据的重要价值在于能够从中发现有用的知识。地学大数据中包含丰富的有用信息，对这些数据进行挖掘，从中发掘出有价值的规律，对于找矿勘查、认识矿床具有重要意义(周永章等， 2018a)。近年来关于大数据在地学中的应用进展迅速，相关的论文也是逐年增加。大数据给地质学这个古老的学科带来了新鲜的血液，正在引发地球科学领域一场深刻的革命(张旗等， 2017)。

大数据方法的一个重要思想就是对于关联关系的重视(罗建民等， 2019)，关联规则挖掘就是这种思维下的一类大数据挖掘算法(Agrawaletal., 1993)，其目的是要从数据中挖掘归纳出有用的规则。关联规则在地质学当中已有一些应用(王贤敏等， 2008; Ereneretal., 2016; Adam, 2016；常力恒等， 2018；刘心怡等， 2019)，如刘心怡等(2019)对区域化探数据进行了关联规则分析，找出了不同元素不同含量区间之间的关联关系。关联规则处理的是离散的类别数据，岩石、矿石的矿物组成数据就属于这类数据。另外，频繁模式挖掘和网络分析也是常用的离散数据挖掘方法。通过频繁模式可以从离散数据集中找出频繁出现的模式、高频次共同出现的离散对象组合，挖掘出的频繁对象组合往往代表着有意义的模式。网络分析用来挖掘离散数据集中个体之间的关联和其中的社团结构。网络分析包括一系列强大的量化分析和可视化方法，这些方法在不同技术和科学领域的大数据展示和解释中得到了大量应用(Newman， 2013；张子柯， 2014； Kolaczyk and Csárdi， 2014)，比如舆情传播分析、疾病传播网络、社交媒体用户之间的联系、恐怖组织的结构以及研究合作者之间的联系等不同主题的数据(刘小鹏, 2010; 吴磊, 2014; 董靖巍, 2016; 乔建琴, 2018)。在这些网络分析应用中，对数据的建模、分析和可视化揭示了复杂系统中以前未被认识的模式和行为。Morrison等(2017)等利用网络分析方法对全球当前已发现的矿物进行了大数据分析，得到了很多有趣的发现，为寻找缺失矿物提供了重要方法。通过网络分析能够对离散数据集中不同个体之间的关系进行可视化，但是要对隐藏在网络中由不同个体构成的社团结构进行进一步的挖掘，就需要用到社团检测算法。社团检测是建立在网络分析基础上的，其目的是为了发现网络图中存在的社团结构。这些由特定离散个体构成的社团往往能够反映一些重要信息。

无论是在岩石、沉积物、陨石还是矿床中，矿物都是以共存集合体的形式存在的。这些共同出现的矿物，并不是随机的，而是按照特定的规律出现在一起，特定类型的矿物总是频繁相伴出现，比如雌黄和雄黄、橄榄石和辉石、方铅矿和闪锌矿等。矿物的共伴生规律可以指示寻找特定的矿产，如果A、B、C 这3种矿物频繁共伴生，那么当一个矿床中出现A、B时，则有很大可能找到C。

以往，对于矿物的共伴生规律，都是通过有限的认识总结得出，或者是通过地球化学反应，从相平衡的角度去研究(陈正， 1984；裴荣富等， 1995；钱汉东等， 2000)，更多考虑的是因果关系，没有从大数据的角度去研究过矿物组成数据。总结出的规律也是一种定性规律，缺乏定量描述。大数据方法更多着眼于其中的关联性而非因果性，经常能够发现数据中隐藏的传统方法不容易发现的规律。本文就是从大数据的角度来研究矿石中的主要组成矿物之间的关系，试图从矿石的矿物组合当中发现有用的矿物共伴生规律，并对这种规律进行可视化。

本文主要着眼于矿石中组成矿物之间的关系，而非所有的岩石，目的是想找出与成矿有关的矿物共伴生规律。数据来源于美国地质调查局的全球矿产资源数据系统(MRDS)，数据多达30多万条，收录了来自于世界各地的各种矿床资源数据，其中就包含了大量的矿石矿物成分数据。对这些数据进行大数据挖掘的研究目前还很少，通过本研究希望能发挥这些数据的价值，从中发现有价值的规律。

传统上矿物之间的共生关系，指的是成矿过程发育的某一阶段共同生成的矿物组合。本文所用的数据当中的矿物组成是没有按照成矿阶段划分的，仅指共同产出在同一矿石中的所有矿物的组合，不涉及成矿阶段的讨论。

1 方法

本文要处理的是离散的矿物组分数据，即矿石中包含哪些矿物，不是矿物含量数据，目的是要从这些离散数据中找出不同矿物之间的关系。大数据挖掘当中，离散数据的挖掘常用的方法有频繁模式、关联规则、网络分析、社团检测等。下面对这些方法做简要介绍。

1.1 频繁模式与关联规则

频繁模式是指数据集当中出现频率不低于用户指定阈值的项目集、子序列或子结构(Zimeketal., 2014)。例如，在购物数据集中，牛奶和面包等一组物品频繁地共同出现，它们就是一个频繁物品集。频繁模式挖掘是数据科学中的一个重要研究领域，应用于许多方面，如推荐系统、生物信息学、商务决策等。

关联规则挖掘也属于频繁模式挖掘的范畴，但关联规则的目的是从数据集中找出频繁出现的规则，而不仅仅是频繁出现的对象集合(Woonetal., 2002)。关联规则是大数据挖掘中一类常用的算法，用于发现隐藏在大数据中的有用规则以及未知关系，其基本思想是根据数据集中其他项的出现来识别预测一个或多个项的出现的规则，是一种无监督的机器学习方法(周永章等， 2018b)。

关联规则挖掘所找到的规则，可以概括为简单的If/Then语句。比如：如果客户购买面包，那么他有70%的可能性购买牛奶。规则可以用X⟹Y(其中X，Y⊆I和X∩Y=φ)的形式表示，X表示if的部分，称为规则前件(LHS)；Y表示then的部分，称为规则后件(RHS)。前件是在数据中找到的项，后件是与前项结合起来发现的一个项目。

为了说明关联规则涉及到的几个基本概念，这里举一个购物的例子。设某商店某次有3个顾客进行了消费，A顾客同时购买了牛奶、黄油和面包； B顾客购买了牛奶、黄油、啤酒； C顾客购买了面包、啤酒、牛奶。则此次被购买物品的集合I={牛奶，面包，黄油，啤酒}称为项集，项集中的牛奶、面包、黄油、啤酒分别是这个项目集中的项，长度为k的项集称为k-项集。一名顾客的一次购物记录称为一个事务。设从中提取了一个规则：{牛奶，面包}⟹{黄油}，则意味着如果购买了牛奶和面包，那么顾客也会购买黄油。为了从所有可能的规则集合中选择有意义的规则，需要定义一些兴趣度度量指标。最常用的兴趣度度量指标有支持度、置信度、提升度、奇异率等。

支持度：定义为项目集X在总项目集里出现的概率，即： supp(X)=num(X)/num(I)。置信度：定义为含有X的项目集中，含有Y的可能性，可以解释为概率P(Y|X)的估计，即： conf(X⟹Y)=supp(X∪Y)/supp(X)。提升度：定义为在含有X的条件下，同时含有Y的概率与Y总体发生的概率之比，即： lift (X⟹Y)=supp(X∪Y)/[supp(X)·supp (Y)]。提升度反映了关联规则中的X与Y的相关性、依赖性,大于1的程度越高表明正相关性越高，小于1且越低表明负相关性越高，等于1表明没有相关性。相比于上面3个指标，奇异率应用较少，它表示在包含Y的事务中找到X的几率除以在不包含Y的事务中找到X的几率，范围:[0.tif，+∞]， 1表示Y不与X关联。

关联规则的常见算法有Apriori(Agrawal and Srikant, 1994)和FP-growth(Hanetal., 2000)等。Apriori算法中最基本的概念是频繁项集，指的是关联规则分析中经常出现在一起的物品的集合。Apriori算法的原理可以概括为：频繁的项集，其子集也是频繁的；反之，一个非频繁的项集，其超集也是非频繁的。基于这个原理，就可以在当前k个频繁项集的基础上通过迭代方法扩展生成k+1个频繁项集。关联规则是由频繁项集生成的，因此算法分为两大步骤，首先是生成频繁项集，之后从频繁项集中找出关联规则。

通过Apriori算法生成的规则，并不是每个都有用，需要用兴趣度度量指标和相关的领域知识来筛选，才能从中找到真正新颖的、有意义的规则。

1.2 网络分析与社团检测

网络分析(汪小帆等, 2006)，也称为社交网络分析、复杂网络分析，是当前数据科学、复杂科学以及物理学等学科当中的研究热点，在大数据挖掘和数据可视化中有广泛的应用。它是通过一系列的节点和连边来构建网络图，利用图来可视化展示和分析事物个体之间关系的方法，可以为一个集合中要素之间复杂的关系提供直观的可视化，从而发现复杂群体中个体之间的关系，发现复杂群体结构中隐含的有趣模式和社团结构。

社团结构挖掘(也称为社团检测或社团发现)是网络分析的一个重要应用，是一种在网络中找出关系密切结点集合(社团)的技术。社团检测算法可以把网络分割为多个子集团，集团内的连边较多，内部结构致密；而集团与集团之间连边较少，结构松散。一般把分割出的集团称为社团，同一社团内的节点之间关系紧密。常用的社团检测算法有Louvain(Blondeletal., 2008)、Infomap(Rosvall and Bergstrom, 2008)、标签传播(Zhu and Ghahramani, 2002)等。本文所采用的社团检测算法是Infomap算法。

Infomap算法(基于节点链接关系随机游走的社团检测算法)是一种基于信息论的网络聚类算法，该算法将寻找图的最优聚类问题描述为寻找图上随机游走的最小信息的描述问题，通过最小化成本函数来找到一个可接受的最优解的近似值，从而分割网络，得到社团。

本文网络分析和社团检测所用的软件为Gephi(Bastianetal., 2009)和R语言的igraph包(Csardi and Nepusz, 2006),频繁模式和关联规则挖掘使用R语言的arules包(Hahsleretal., 2018)。

2 数据

2.1 数据简介

数据来源于美国地质调查局(USGS)网站公开发布的全球矿产资源数据系统-MRDS(https://mrdata.usgs.gov/mrds/)。MRDS数据系统所收录的数据来自于世界各地，包括金属和非金属矿产数据，数据集不断更新，目前共包含304 633条数据。其中描述的内容包括所收集的矿床(点)数据的位置、产出矿产类型、矿物组成、赋矿围岩等基本信息。本文关注的是每条数据中矿石的矿物组成，包括矿石矿物和脉石矿物，将脉石矿物和矿石矿物合并起来，代表矿石的每条数据中的矿物组成。这些数据来源复杂，数据质量不一，因此，为了提高关联规则挖掘的准确性，要对这些数据进行数据预处理，剔除错误数据、冗余数据、无效数据。

2.2 数据预处理

(1) 从MRDS数据库中提取其中的矿石矿物和脉石矿物数据，将二者合并得到矿石矿物成分数据，如表1。

表 1 矿物组成数据示例Table 1 Example of mineral composition data

(2)本文不探讨能源、建材类的矿产，因此，对于原始数据中的这类数据进行筛选剔除，剩下181 003条数据。

(3)对这些数据中存在矿物名称错误的、只有单个矿物的、不是矿物的词组混进矿物组成数据的等等各种错误的矿物组成数据进行剔除。

(4)对数据中的标点符号进行替换处理，形成词组，方便算法进行处理。

(5)将以上处理过的数据转换为逗号分隔的txt文件，作为大数据挖掘的输入数据。

3 结果与讨论

3.1 频繁模式挖掘

对经过预处理的数据进行了词频统计，结果显示预处理之后的数据集中囊括的矿物共包括652种，其分布呈现出指数分布规律(图1，图中横坐标是按照数据库中的矿物统计频次排名的名次，纵坐标为出现次数)，说明少数矿物在各类岩石矿石中广泛存在(如石英)，大部分矿物则只出现在特定的岩石和矿石中，分布比较局限和稀少。为便于从整体上观察数据集当中的矿物分布情况，对词频统计结果可视化就得到了词云图(图2)。词云图中字体越大代表出现在各种矿石中的频次越多。从图2中可以看出，词云图基本符合了我们对于金属矿床主要矿物组合的认识，最多出现的是石英，其次是自然金、黄铁矿、黄铜矿、方铅矿等等，比较罕见的矿物出现的频次较低，在词云图中不显著。

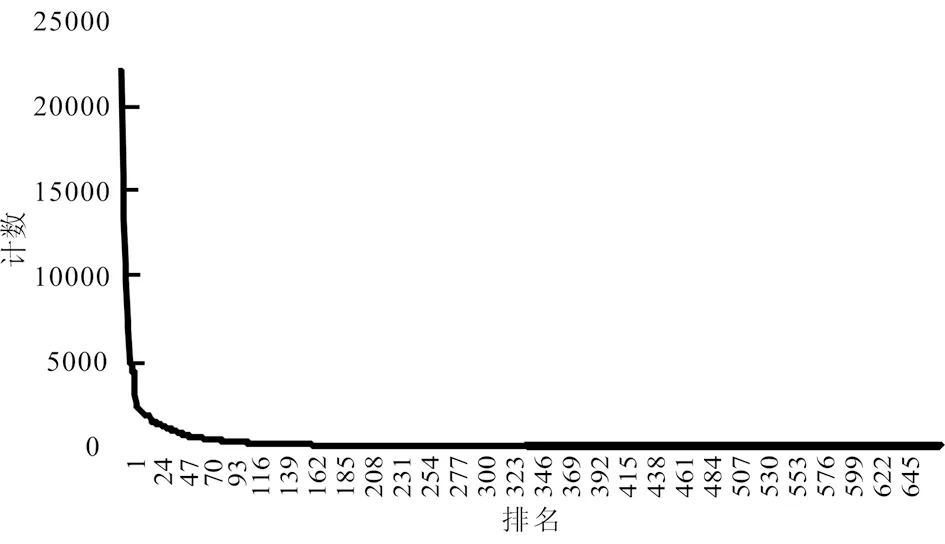
图 1 矿物出现频次统计Fig. 1 Frequency of minerals in ores

图 2 词云图Fig. 2 Word cloud

通过R语言的arules包来进行频繁模式和关联规则挖掘，主要用到两个函数eclet和aporior。前者用来找出频繁项集，后者用来找出关联规则。表2列出了出现频次排名前15的频繁项集。

从表2可以看出，出现次数较多的矿物组合基本都是由黄铁矿、黄铜矿、闪锌矿、方铅矿、石英、方解石这几种矿物中的几个组合而成。这几种矿物在大多数金属矿床中都是主要的组成矿物，且往往都是以矿物组合的方式出现的，这与金属矿床的矿物组成规律是相符的。

3.2 关联规则挖掘

仅仅通过频繁模式，只能找出所有矿物组合当中频繁出现的那些，这样得到的只是一些矿物组合。而通过关联规则，则可以找到矿物组合规则。这里的规则，指的是一种if⟹then形式的推导规则，即如果一个矿石中出现A矿物，那么有多大可能性也出现B矿物。这种规则相比于前面的矿物组合更有意义，更实用。

表 2 频繁模式排序列表Table 2 Frequent items sorted by support

这里的关联规则挖掘使用aporior函数，设置参数为：最小支持度0.001，最小置信度0.75，最小规则长度2，最大规则长度5。计算结果显示，共找到6 728条规则。如此多的规则，如果逐个检查找出有用规则，工作量会非常大，因此要利用兴趣度度量指标，结合地质学知识去筛选出有用的规则。这里我们主要用支持度、置信度、提升度、奇异率几个指标来对规则进行排序和筛选，先按照提升度进行排序，选择排序靠前且有地质意义的规则若干，结果见表3。

从表3中可以看出，{雌黄}⟹{雄黄}这条规则的提升度最大，是一条强关联规则，说明雌黄和雄黄存在很强的共生关系，这与人们通常的认识是一致的。还有{绿纤石}⟹{绿帘石}等等规则，也符合自然界当中矿物的共伴生规律。这说明通过关联规则算法提取出的规则经过兴趣度筛选，能够找出有用的矿物共伴生规律。

另外按照另一个重要的综合性指标——奇异率进行了排序，选择一部分奇异率大且有地质意义的规则，结果见表4。表4中的很多规则，也同时出现在表3中，这说明较强的关联规则在提升度和奇异率两种兴趣度度量指标上都得分较高。在选择有用关联规则的时候，可以结合多种兴趣度度量指标以及实际地质规律进行筛选。

表 3 据提升度排序筛选的规则列表Table 3 Rules sorted by lift

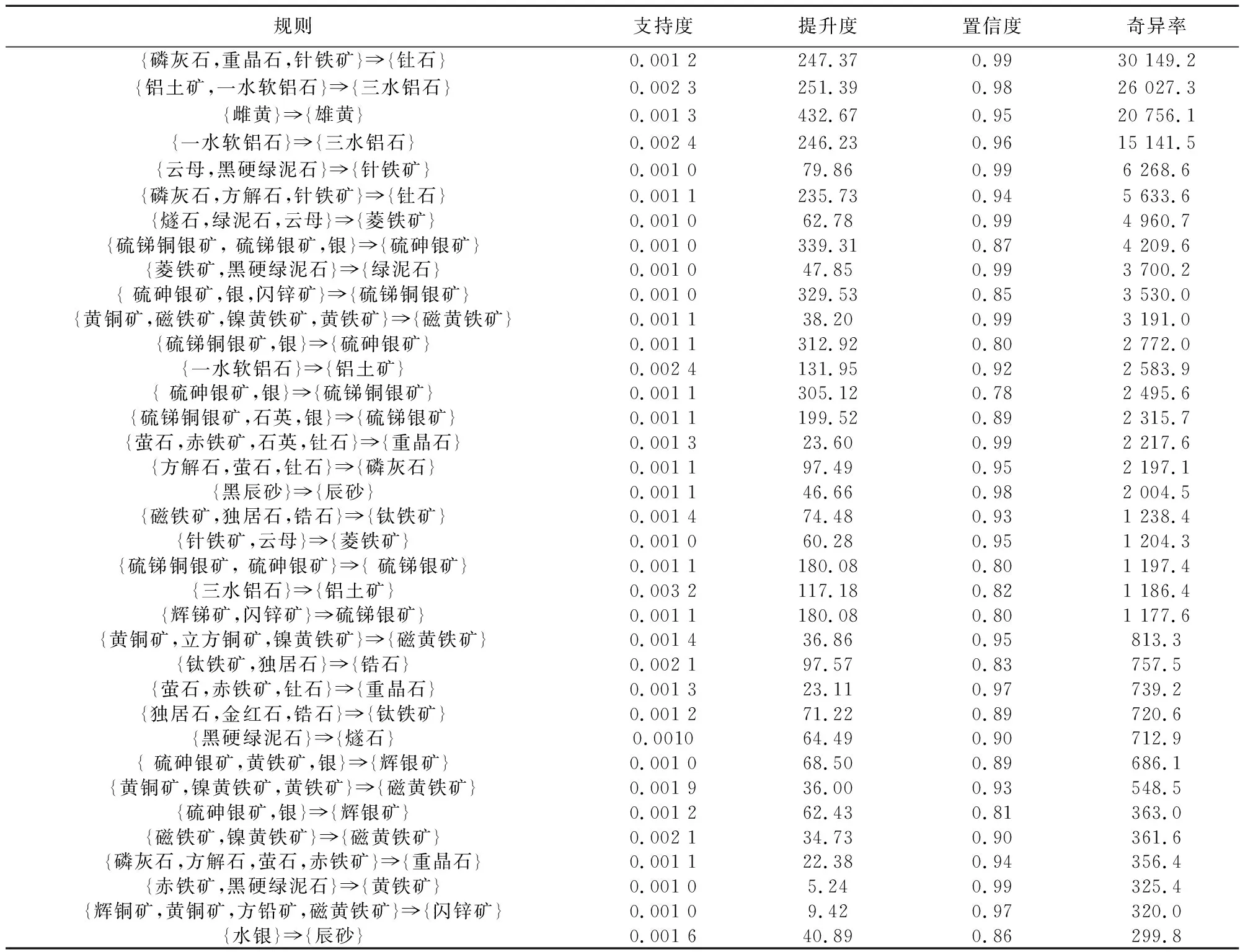
表 4 根据奇异率排序筛选的规则列表Table 4 Rules sorted by odd sratio

由上可见，通过关联规则挖掘筛选出来的规则符合矿物学规律，反映了矿物共伴生的客观规律。比如常见的{雌黄⟹雄黄}、{水银⟹辰砂}这些规则已广为人们熟知，但除了这些广为人们熟知的规则之外，还有很多有用的规则，限于篇幅只在本文列出了其中兴趣度较大的一部分。这些规则对于认识矿物的共伴生规律很有意义，可以用来指导寻找特定的矿产资源。如{赤铁矿，黑硬绿泥石}⟹{菱铁矿}这条规则，当在岩石中看到赤铁矿和黑硬绿泥石的时候，就说明找到菱铁矿的可能性很大，通过这条规则可以帮助寻找菱铁矿。

通过经验总结出的矿物共伴生规律是定性的规律总结，而通过关联规则挖掘出的共伴生规则，则是一种定量化的规则，通过兴趣度度量指标能够定量地表征规则的强弱。经验总结的矿物共生规则只是一个矿物共生集合，但基于关联规则找出的规则，则是一种推理规则，能够根据规则前件推导出规则后件。总的来说，基于关联规则从矿石矿物组分大数据中挖掘出的规则更加定量化和精细化。

3.3 网络分析与社团检测结果

构建网络的基本要素是节点和边。在矿石矿物网络分析当中，网络的节点为单个矿物类型，网络的边则为矿物两两之间的关联指标，在这里用前面关联规则中计算的提升度作为关联性度量指标。具体构建网络的方法为：利用关联规则算法找出所有长度为2的规则，剔除掉这些规则当中支持度太小的(支持度太小说明这些规则不具有普遍意义)，利用这些规则的提升度作为网络图连边的权重来构建网络，最终得到一个由315个节点和8 872条边构成的复杂网络。为了突出重要关联，对网络的边利用边权重设置阈值进行过滤，得到一个简化的网络。之后利用ForceAtlas2力导向算法(Jacomyetal., 2014)重构网络布局，该算法可以根据网络节点属性和边的权重调整网络结构，使得相互关系较近的节点彼此靠近，关系疏远的节点相互疏远，从而对网络中节点之间的关系进行可视化，结果如图3所示(因要素太多，图中仅展示局部)。

通过上面构建的网络图可以对矿石中主要成分矿物之间的关系进行可视化。这些矿物节点在网络中的聚集分散模式在一定程度反映了自然界中矿物之间的相似性和共伴生规律。比如正长石、奥长石、微斜长石3种矿物差别小，相似度高，在网络图(图3)中彼此靠近。再比如伊利石、蒙脱石、高岭石均属于粘土矿物，经常共生在一起，因此在网络图(图3)中彼此靠近。橄榄石与高岭石等粘土矿物相似度低，不存在共伴生关系，所以在网络图中相距较远。矿物在网络图上的这种亲疏模式，主要受它们的成因、晶体结构类型、化学成分、矿物形成条件等的控制。

从网络图中还可以看出其中存在明显的社团结构，特定的矿物倾向于聚集在一起形成社团(即那些局部紧密连接的区域)，如图3b中的{铝土矿、三水铝石、一水软铝石、锐钛矿}这个矿物组合社团。同一社团内的矿物距离较近，连边较密集，相比于社团外的矿物具有更密切的联系；不同的社团之间则彼此距离较远，连边稀疏，联系不密切。这些社团不是随机组合的，每个社团内部的矿物成员具有一定的相似性和共性，代表特定的矿物组合。

虽然从网络图中能够直观看到存在社团结构，但仅通过观察网络去发现社团效率很低，难以处理较复杂的网络，而且不够准确。为了更好地找出网络中的社团，利用前文提到的Infomap算法对前面构建的网络进行社团检测，得到的典型社团如表5所示。Infomap算法属于聚类算法，其结果可用聚类谱系图的形式来可视化(图4)。本文涉及的矿物多，限于篇幅，表5和图4中仅展示了部分结果。

从表5和图4中可以看出，这些社团反映了自然界中矿物之间的相似性和共伴生关系。同一个社团内的矿物往往具有共同的成因(比如铝土矿中的主要含铝矿物)，或者相近的化学成分(比如红柱石、蓝晶石、夕线石)，或者相近的形成条件(比如钾盐、芒硝、光卤石、岩盐等矿物组合)，或者属于同一共伴生组合(比如雌黄、雄黄)。

这里要注意，虽然同一社团内的矿物之间存在密切联系，但一个矿物社团并不一定就是一个矿物共伴生组合。社团结构指的是网络中一组连接紧密的节点所组成的团体，社团里面的矿物连边更多，联系更密切，但并不是矿物两两之间都具有连边。而共伴生组合其实表现在网络图中是一个各个成员全连接的子网络结构，即所谓的团，要求这个组合中的成员两两之间都具有大于阈值权重的连边，比如图3中橄榄石、辉石、尖晶石三者互相连接，形成共生组合。

以上网络分析和社团挖掘结果说明，通过网络分析可以对矿石中主要矿物之间的关系和共伴生规律进行可视化，通过社团检测可以找出哪些矿物之间存在密切联系。