基于颅骨及四肢骨骨折程度推测坠落高度

高 飞，杨 宁，戴运达，张启宇，汤艺坤，赵 虎

（1.中山大学中山医学院法医学系//广东省法医学转化医学工程技术研究中心，广东广州 510080；2.广州市公安局越秀区分局，广东广州 510055）

高坠案件是命案法医现场的常见案件类型，多发生在人群密集的居民小区［1］、医院［2］等公众场所，该类案件的死亡方式推定一直是国内外法医病理学与法医现场学的重点与难点之一。高坠案件坠落起点往往具有不确定性，这妨碍了案件死亡方式及时有效的推定。根据人体损伤程度与损伤特点推断坠落高度，从而进一步锁定坠落起点的工作思路，已成为法医高坠研究的有效策略。2016 年Kusior 等［3］提出损伤的数量、损伤程度的定量和损伤的特定阈值，有助于坠落高度的推定。目前国内高坠研究多以骨折的严重程度衡量人体损伤程度［4］，颅骨骨折与四肢骨骨折是国内高坠案件常见的骨折类型［1］。因此本文重点分析颅骨及四肢骨的骨折严重程度与坠落高度的相关性，为高坠案件的坠落起点推定奠定科学依据。

1 材料与方法

1.1 一般资料

收集2014 年6 月至2018 年5 月发生在广州市越秀区、具有颅骨骨折和（或）四肢骨骨折的高坠案例共163 例，已知坠落高度（≤70 m）和个人年龄且损伤数据明确的案例133 例，其中无中间障碍物且接触面为硬质平面的案例66 例（现场勘验时死亡60 例，幸存6 例）。

具有颅骨骨折的案例48 例（男=26，女=22），具有四肢骨骨折的案例58 例（男=36，女=22；上肢骨=34，下肢骨=47）。共收集206个有效骨折数据（男=114，女=92），其中颅骨骨折62 例（颅骨穹隆部=19，颅底=23，面颅=11，下颌骨=9），四肢骨骨折144 例（左/右上肢骨骨折=35/25，左/右下肢骨骨折=42/39，骨盆骨折无侧别=3）。

1.2 方 法

为了控制模型的影响因素，本研究重点分析无中间障碍物且接触面为硬质平面的66 个高坠案例，排除坠落高度未知或无法明确的案件数据。样本人口社会信息包括案件性质、性别、年龄及坠落高度，同时收集现场图片、监控录像、法医学检验记录及病历资料供进一步分析。

针对《人体损伤程度鉴定标准》（以下简称《标准》）［5］的线性、粉碎性及开放性3 种骨折形态类型分别计1～3 分，并参考《简明损伤定级标准2005》（Abbreviated Injury Scale 2005，简称AIS2005）［6］的骨折分级与定量方法。结合Casali 等［7］（2014）的颅骨分区方法，将颅骨骨折区域分为颅骨穹隆部、颅底、面颅（鼻骨、颧骨及上颌骨）和下颌骨共4 个部分。根据赵桂范与杨娜［8］（2007）的多刚体人体模型的13 个自由度（肩、肘、腕、腰、髋、膝、踝），区分四肢骨的骨折区域。采用AIS2005-MAIS（Maximal AIS）标准法对选定区域的多发损伤进行定量，并将颅骨骨折和四肢骨折各个损伤区域的MAIS 值分别相加计分，表示骨折的总严重程度（简称骨折程度）。

计分结果如下，颅骨骨折形态：面部轻微骨折（眶骨1 例，计0.5 分）、线性骨折（颅底23 例，颅骨穹隆部3 例，上颌骨1 例，下颌骨4 例，计1 分）、粉碎性或凹陷性骨折（颅骨穹隆部6 例，面颅2 例，下颌骨5 例，计2 分）、开放性骨折/面颅广泛性损毁/颅骨整体变形（颅骨穹隆部4 例，面颅5 例，计3 分）、面颅广泛性损毁伴开放性骨折（2 例，计4 分）、颅骨穹隆部广泛性损毁伴开放性骨折（1 例，计6 分）和颅骨穹隆部广泛性损毁伴开放性骨折合并整个脑组织从颅腔脱离（5 例，计8 分）；四肢骨骨折形态主要包括关节骨擦感（11 例，计0.5 分）、关节畸形（18 例，计1 分）、关节开放性骨折（49 例，计2 分）和线性骨折（2 例，计1 分）、骨折畸形（40 例，计2 分）、开放性骨折（24 例，计3 分）

1.3 统计方法

所有数据均采用SPSS 20.0（IBM Corporation，GZ，GD，CHN）软件进行统计分析，统计方法包括独立样本t检验、Pearson 相关分析、多重线性回归分析。均值采用表示，P<0.05 表明差异有统计学意义。

2 结果

高坠者男40 例（60.6%），女26 例（39.4%）；年龄7.0～92.0（45.6 ± 18.1）岁；坠落高度的均数为3.5～63.7（19.2 ± 12.7）m。颅骨骨折程度的均数为0～9.0（2.1±2.3）分，四肢骨骨折程度的均数为0～14.5（4.2±3.2）分。死亡方式以自杀最多59 例（89.4%），意外7例（10.6%）。

对不同性别与案件性质的年龄、颅骨骨折程度、四肢骨折程度及坠落高度进行比较，发现自杀组的四肢骨折程度明显高于意外组，其他差异无统计学意义（表1）。

Pearson 相关分析显示，坠落高度分别与颅骨骨折程度、四肢骨折程度呈显著正相关（r1=0.698，r2=0.780，P<0.05），提示颅骨及四肢骨骨折程度均随坠落高度的增加而加重。

再以坠落高度Y 为因变量，以颅骨骨折程度X1、四肢骨骨折程度X2、年龄X3、性别的虚拟变量X41（男=1，女=0）和X42（女=1，男=0）为自变量，进行多重线性回归分析，采用逐步法对自变量筛选，变量X2、X1、X3依次进入回归模型，X41和X42未进入回归模型，获得最终回归模型（表2）。回归方程：=6.660+2.843X1+2.664X2-0.099X3。误差s=4.577 m，校正R2=0.871，F（3，62）=146.792，P<0.001。

根据本文的适应条件，我们将上述回归方程进行实际案例验证。经查阅高坠案例报道的相关文献，发现符合本研究回归方程限制条件的文献共6 篇，包含7 个案例［9-14］，其中案例4 的高度为宾馆3 层，根据案例7 的宾馆4 层高度13.5 m 进行了估算，案例4 的高度约为10.1 m。将文献中的人体骨折程度与年龄数据代入回归方程，获得推测高度（prediction of falling height，PH），将其与真实高度（actual falling height，AH）进行比较验证，验证结果详见表3。真实高度与推测高度的差值在（-1.402～2.209）m之间，达到了1层以内的精确度［3］，说明本研究的回归方程具有较好的应用价值。

表1 不同性别与案件性质的比较Table 1 Comparison of genders and the nature of 66 cases（）

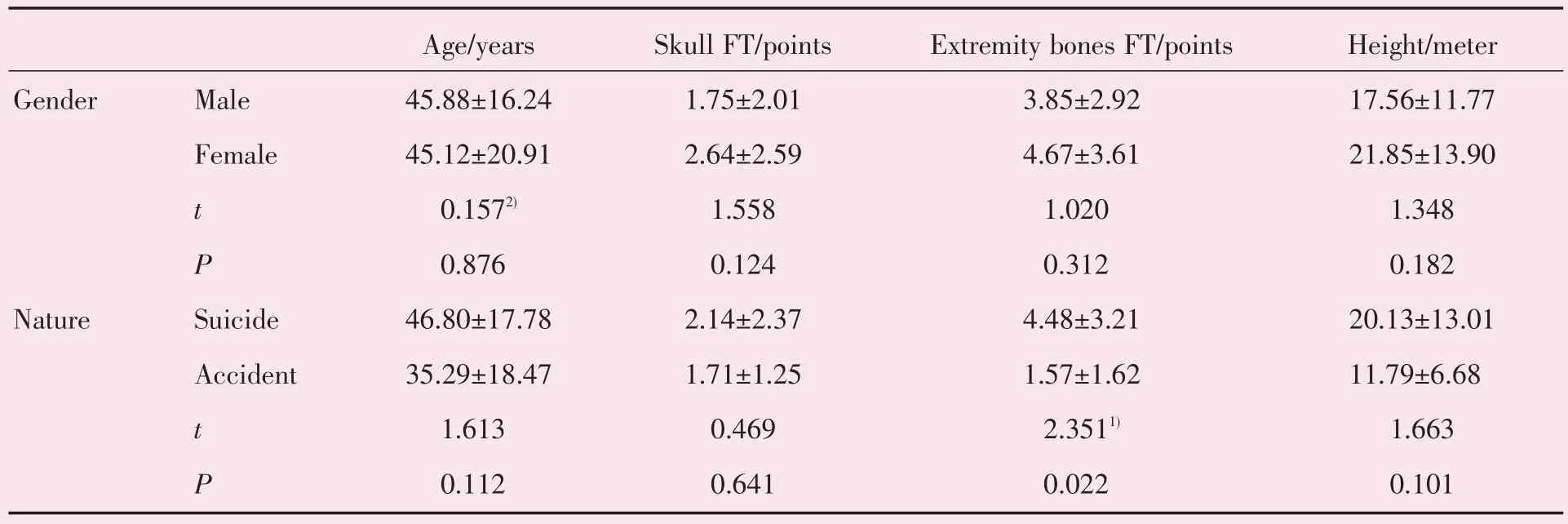
表1 不同性别与案件性质的比较Table 1 Comparison of genders and the nature of 66 cases（）

FT：the total severity of fractures；1）P<0.05；2）Levene's test for equality of variances，P<0.05

表2 坠落高度的多重线性回归变量筛选结果Table 2 Results of multiple linear regression variable screening for falling height （n=66，meter）

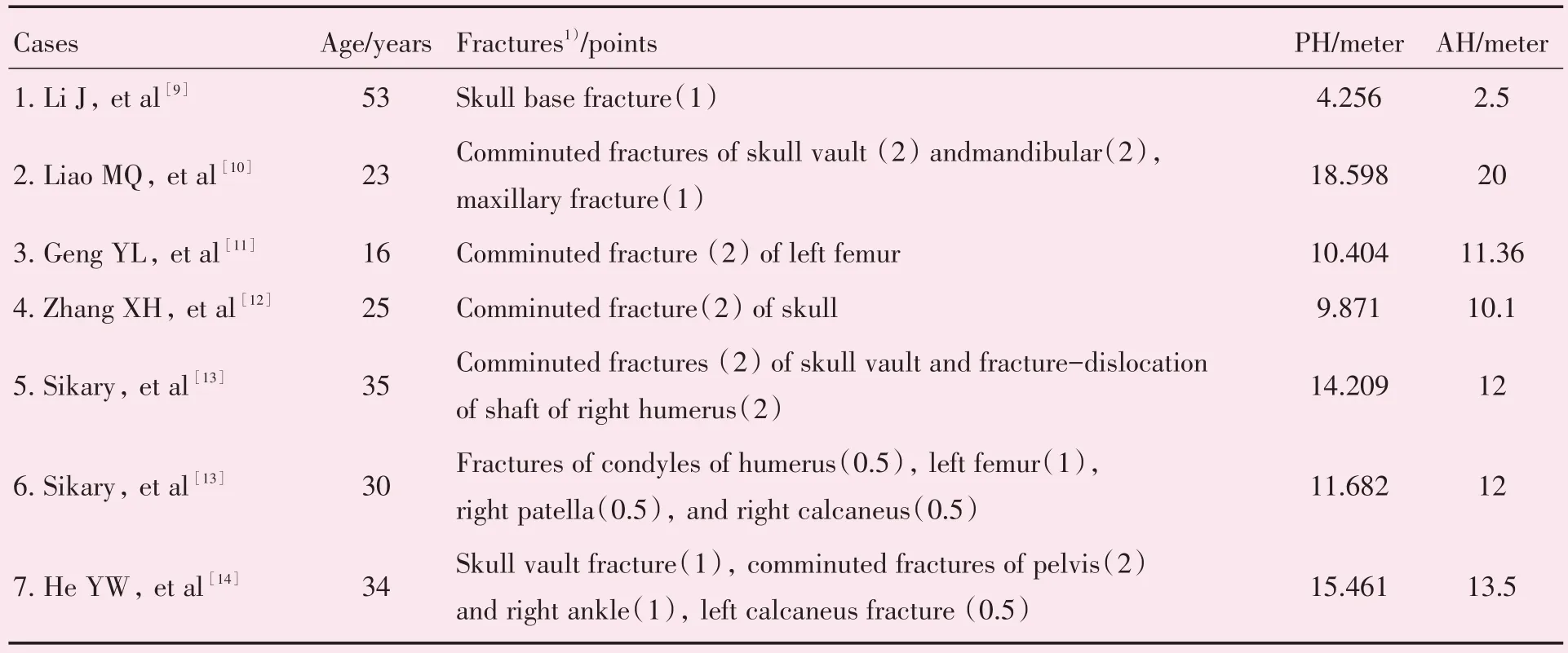
表3 坠落高度回归方程的案例验证结果Table 3 The application effect of cases data from published articles in the regression model

3 讨论

本研究66 例高坠案例基本信息显示，总体年龄（45.6±18.1）岁，坠落高度（19.2±12.7）m，范围（3.5～63.7）m。总体中男性居多，死亡方式以自杀为主。两性及死亡方式的比较结果显示，年龄、坠落高度均差异无统计学意义。自杀组的四肢骨折程度，明显高于意外组。相关分析提示颅骨骨折程度和四肢骨骨折程度均随坠落高度增加而加重，这与Petaros 等［15］关于颅骨发生粉碎性骨折相比线性骨折需要更高的坠落高度的观点一致，与Kusior 等［3］研究发现四肢开放性骨折发生的坠落高度比四肢粉碎性骨折更高的报道相符。

回归方程的R2=0.871，拟合优度极佳，说明颅骨骨折程度、四肢骨骨折程度和年龄可以解释87.1%的研究样本的坠落高度变异，误差s=4.577 m，小于Lau G 模型的误差（s=5 m）。回归方程的截距为6.660 m，说明控制年龄变量的前提下，6.660 m 以上高度坠落的人体颅骨和四肢骨的骨折程度与坠落高度具有线性相关关系。根据归回方程可以得出，最小年龄7.0 岁个体从5.967 m的高度坠落可能出现无法检见颅骨骨折或四肢骨骨折的情况，随着年龄的增加该高度临界值会降低，当个体年龄超过67.3岁时，高度数值接近0 m，说明年轻人从较低的高度坠落时可以通过下肢的缓冲作用避免骨折发生，而67.3 岁以上的老年人在摔跌（高度为0 m）时颅骨或四肢骨就有较大可能发生骨折，与Con 等［16］关于较低高度（高度范围0～12 m，均值2.98 m）坠落的65 岁以上老年人特别容易受伤且损伤程度更重的观点相符。颅骨和四肢骨的骨折程度的偏回归系数分别为β1=2.843 m和β2=2.664 m，说明控制年龄变量的前提下，颅骨的骨折形态类型的特定高度阈值与2.843 m 有关，四肢骨的骨折形态类型的特定高度阈值与2.664 m有关，据此我们可以根据已知年龄个体的骨折形态类型计算该类骨折发生的高度，进行高度阈值检验。由表1和案例筛选条件可知，回归方程的应用需符合以下适应条件：①个体年龄7.0～92.0 岁；②坠落高度3.5～63.7 m；③坠落过程无中间障碍物；④接触面为硬质平面。

回归模型的特定高度阈值检验：颅骨线性骨折的AIS评分2分，AIS2005-MAIS《标准》法的定量值为1 分，高度阈值为2.843 m，与Rowbotham 等［17］研究发现颅骨线性骨折好发于1.5～3.0 m 的高度坠落的结果相符，而汪家文［18］的研究显示不一样的结果，他发现1.3 m 高度坠落，颅骨已经出现线性骨折，1.8 m 出现线性骨折间隙明显增宽，这可能与作者将头皮与颅骨分离导致头皮的保护颅骨作用下降［19］有关。颅骨粉碎性骨折的AIS 评分3 分，AIS2005-MAIS《标准》法的定量值为2 分，高度阈值5.686 m，与Lefèvre 等［20］关于颅骨粉碎性骨折不太可能发生在2.5 m 以下的高度坠落的观点一致。关节骨折的AIS 评分1 分，AIS2005-MAIS《标准》法的定量值为0.5 分，高度阈值为1.332 m，骨盆骨折为四肢骨线性骨折，AIS2005-MAIS《标准》法的定量值为1 分，高度阈值2.664 m，与Rowbotham 等［17］关于股骨转子间骨折多发于1.5 m以下的高度坠落和1.5 m 以下的高度坠落不足以导致骨盆骨折的研究结果一致。经过文献高度阈值检验，颅骨骨折程度和四肢骨折程度的偏回归系数与早期文献关于骨折形态与高度的相关关系的报道一致，说明回归方程在法医高坠研究领域同样具有应用价值。Casali 等［21］2019 年通过对385 例高坠者损伤数据的回顾性分析，建立人体损伤程度推测坠落高度的线性回归模型，年龄的回归系数为-0.097 与本文的结果（β3=-0.099）基本一致，面颅和骨盆的偏回归系数显示不一样的结果，分别为1.073 m 和1.921 m，这可能与骨骼损伤分级标准不同有关。

研究表明多刚体人体模型可以反映汽车与人碰撞过程中人体受力情况和人体损伤机制［8］，也可应用于高坠案件分析，重建人体跌倒的不同情景［22］。Papadakis 等［23］采用相似的骨折分区方法研究骨折与坠落高度的相关性，发现肢体和骨盆的骨折频率与坠落高度呈正比，本文根据多刚体人体模型分区的四肢骨骨折程度与坠落高度同样具有正相关关系，说明四肢骨骨折的多刚体人体模型分区法在法医高坠研究领域具有一定的适用性。

我们的研究提示AIS2005-MAIS 标准法评估的颅骨骨折程度与四肢骨骨折程度是推测坠落高度的良好指标，并建立了拟合优度较好的推测坠落高度的数学模型［21］，但也存在以下局限性。首先，与高度相关的损伤未全部纳入研究范围；其次，多刚体人体模型在法医高坠研究中应用的有效性尚需验证。本研究的损伤数据来源于高坠现场的尸体检验，轻微骨折可能被忽略。