合肥二级阶地黏土层物理力学指标概率统计及相关性分析
2020-10-12李飞飞牛真茹
李飞飞 牛真茹 王 涛
(1.北京城建勘测设计研究院有限责任公司,北京 100101; 2.天津华北地质勘查总院,天津 300181)
引言
近年来,随着国家基础设施建设的快速发展,涌现许多规模较大的轨道交通、市政管廊、高层建筑等工程,这些工程对基础选型、地基承载力、边坡稳定性、基坑变形沉降等方面的要求较高,这就需要提供更为精准的岩土物理力学参数来指导工程建设。
岩土体是一种在自然条件下形成的工程材料,一般具有随机性和空间变异性等特点,其物理力学参数通常可以通过原位测试和室内试验等手段来获取,但由于岩土体沉积环境的差异性和自身结构的空间变异性,导致岩土参数表现出一定的随机性和不确定性,需要因地研究、区别对待。大量统计结果表明,岩土体各物理力学指标之间具有一定的关联,服从某种概率分布特征[1]。姜燕等通过对岩土参数进行统计分析发现,岩土参数多服从对数正态分布[2];高大钊通过对岩土参数变异性进行分 析,给出上海地区岩土参数的分布特征[3];潘天有通过对土的物理力学进行分析,提出岩土物理力学之间存在相关性和联系性[4];王永洪等分别对北京、南京和沈阳的岩土体物理力学参数进行研究,分析了各指标间的相关性[5-7];张世荣等通过对南宁市岩土体进行地质单元划分,对其数据进行统计,得出了南宁市岩土物理力学指标参考表[8];吴长富等选取GB50021—2001《岩土工程勘察规范》中的岩土参数标准值进行分析,得到了相关计算式[9]。目前,对土体的研究主要按地域进行,通常将特定沉积年代、相同沉积环境下的土体作为研究对象进行统计分析;现行的相关规范和手册也仅对各个地区的物理力学指标进行总结,很少通过划分地质单元进行土体性质分析。
目前,合肥市正处于轨道建设大发展的阶段,市区内地铁车站和盾构区间大多位于二级阶地黏性土中。选取合肥二级阶地第四纪晚更新世黏土层作为研究对象,对二级阶地黏土层物理力学指标进行统计分析,研究结果对黏土层各物理力学参数的选用具有一定的参考和借鉴意义。
1 土体物理力学指标统计分析
1.1 合肥二级阶地地层典型特征
合肥地处二级阶地之上,境内水系较发育,主要河流为南淝河。依据地形地貌、地层岩性、含水层分布特征将合肥城区地貌类型划分为河漫滩和阶地地貌。合肥地铁4号线呈东西转南北的L形,线路与地貌单元关系如图1。
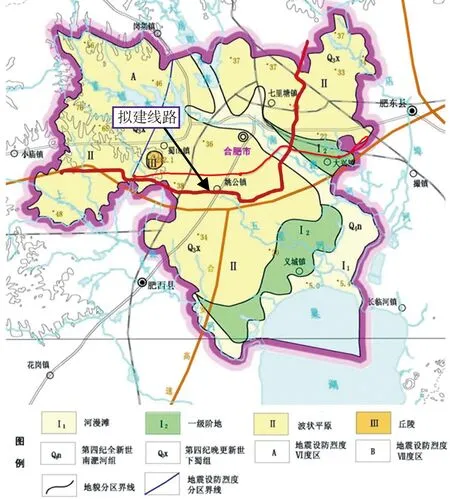
图1 线路与第四纪地貌单元位置关系
研究区属华北鲁西地层分区的长丰小区,经历史沉积,堆积巨厚的中、新生代陆源碎屑岩。根据合肥地铁4号线工程沿线勘探孔所揭露的地层,二级阶地岩土层主要为人工填土层、第四系上更新统冲洪积层、白垩纪砂质泥岩。其中,第四系黏土层埋深一般为5~30 m,黄褐-褐黄色,可塑-硬塑,局部坚硬,通常具有一定的膨胀性。
1.2 物理力学指标统计分析
共收集二级阶地同一地质单元共计716个勘探孔(1 179个)土样数据,应用SPSS统计分析软件,对各岩土物理力学参数进行统计分析,统计结果见表1。

表1 合肥二级阶地黏土物理力学性质指标统计
由表1可以看出,合肥二级阶地黏土层主要有以下特征。
(1)含水量低、土体致密
土体天然含水率为14.8%~38.6%,统计平均值为24.2%;孔隙比为0.634~0.884,统计平均值为0.785。土体含水率低,孔隙比小,土体较致密。
(2)可塑-硬塑状态
土体液性指数为-0.38~0.65,统计平均值为0.12,土体多呈可塑-硬塑状,局部坚硬,主要表现为硬塑状。
(3)中压缩性
土体压缩模量为5.1~15.9 MPa,统计平均值为10.0 MPa,属中压缩性土。
(4)抗剪强度高
土体快剪指标黏聚力为22.9~124.5 kPa,统计平均值为73.5 kPa,内摩擦角为8.5°~24.7°,统计平均值为15.9°,抗剪强度较高。
(5)弱-中膨胀性
土体自由膨胀率为28.5~77.5,均值为48.5,根据GB50112—2013《膨胀土地区建筑技术规范》,合肥地区黏土层为弱-中膨胀性土。
(6)变异系数小
土体物理性质指标变异系数为0.09~0.12,土体性质相近;力学指标变异系数为0.16~0.35,力学性质差异较小。
2 土体概率分布特征
概率论是研究随机性现象的一门学科,采用建立概率分布模型的方法进行拟合分析。由于土体参数具有一定的变异性,故可以通过数理统计的方法对土体岩土参数合理统计分析,掌握土体的规律性变化[11-12]。前人通过对大量岩土参数进行统计分析,发现岩土体指标主要服从正态分布[13-15]。
正态分布又称高斯分布,其概率密度函数为

(1)
式中,u为平均值;σ为标准差。
峰度-偏度检验法是一种检验是否服从正态分布的方法[16]。其中,偏度是反映总体分布的非对称性的一种度量,峰值是反映密度函数 “峰”的尖削程度的一种度量,若统计数据的偏斜度和峰值越接近0,则认为其越服从正态分布[17-18]。当需要进一步反映总体概率分布函数时,可采用绘制概率分布直方图的方式。
对合肥二级阶地黏土层1 179个土样数据进行统计分析,采用峰度-偏度检验法对其指标进行正态分布检验,结果见表2。

表2 合肥黏土物理力学性质指标统计分布模型
由表2可知,合肥二级阶地黏土层含水率、液限、塑性指数、压缩模量、黏聚力、内摩擦角服从正态分布;塑限、液性指数近似正态分布;湿密度、孔隙比、压缩系数不服从正态分布。选取表2中典型土体参数含水率、压缩模量、液性指数和孔隙比绘制概率分布直方图,如图2~图5。
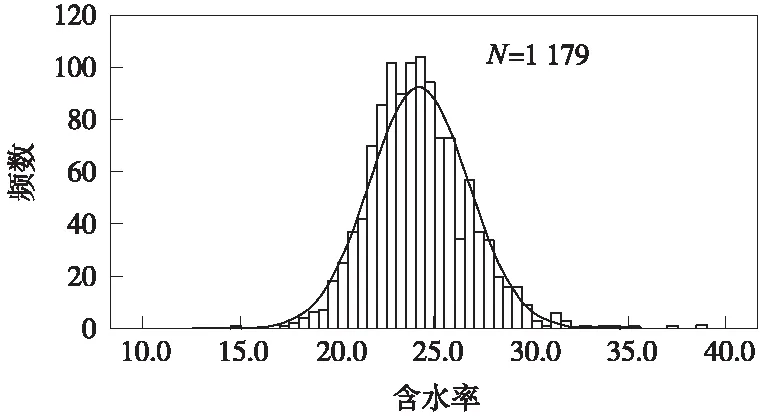
图2 含水率直方图

图3 压缩模量直方图

图4 液性指数直方图

图5 孔隙比直方图
由图2~图5可知,含水率和压缩模量服从正态分布,液性指数基本服从正态分布,孔隙比不服从正态分布,与表2中统计的土体指标分布形态相吻合。
3 土体物理力学指标相关性分析
研究表明,岩土指标参数之间通常存在一定关联,通过回归分析可建立各指标间的经验公式,为工程设计提供参考。选取合肥二级阶地黏土层大量试验数据,对其指标参数间的相关性进行分析。
3.1 物理性质指标之间相关性
采用线性回归的方法对含水率、湿密度、孔隙比、液限、塑限、塑性指数、液性指数等指标进行分析,并建立回归方程,结果如图6~图8。

图6 含水率与液性指数相关性
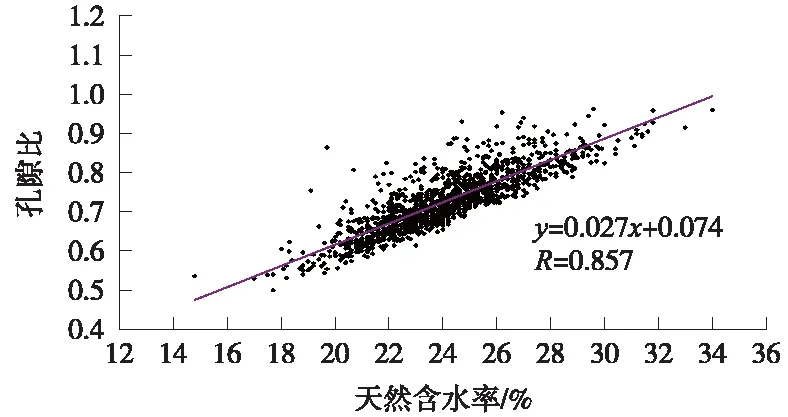
图7 含水率与孔隙比相关性

图8 塑性指数与液性指数相关性
由图6~图8可知,含水率与液性指数之间为正相关关系,表现为随着含水率增加,土体液性指数增大,土体状态变差,二者相关系数R为0.62,相关性较强,回归方程为
y=0.030x-0.629
(2)
含水率与孔隙比之间呈正相关关系,相关系数R为0.857,相关性较强,回归方程为
y=0.027x+0.074
(3)
液性指数与塑性指数之间呈负相关关系,相关系数R为-0.36,相关性中等,回归方程为
y=-0.01x+0.357
(4)
3.2 力学指标之间相关性
选取压缩模量、黏聚力、内摩擦角等力学指标进行相关性分析,并建立回归方程,结果见图9、图10。

图9 黏聚力与压缩模量相关性

图10 黏聚力与内摩擦角相关性
由图9、图10可知,黏聚力与压缩模量之间呈正相关关系,表现为随着土体强度的增加,压缩性变小,与实际相符。二者相关系数R为0.77,相关性较强,回归方程为
y=4.74x+23.42
(5)
剪切指标中,黏聚力与内摩擦角相关性关系不明显。
3.3 物理性质指标与力学指标的相关性
选取含水率、孔隙比、压缩模量、黏聚力等指标进行相关性分析,并建立回归方程,结果见图11~图14。

图11 含水率与黏聚力相关性

图12 孔隙比与黏聚力相关性

图13 孔隙比与压缩模量相关性

图14 含水率与压缩模量相关性
由图11~图14可知,含水率、孔隙比与黏聚力之间均呈负相关性,表现为土体强度随着含水率增加或孔隙比增大而减弱,与实际相符。其中,含水率与黏聚力相关系数R为-0.54,相关性中等,回归方程为
y=-4.97x+190.29
(6)
孔隙比与黏聚力相关系数R为-0.74,相关性中等,回归方程为
y=-127.18x+164.49
(7)
孔隙比、含水率与压缩模量之间相关性不明显。
4 结论
(1)合肥二级阶地晚更新世黏土层土体参数变异系数较小,土体性质差异性小,工程性质相近。
(2)黏土层物理力学指标间相关性表现为:土体物理性质指标间多为中等-强的相关性;力学指标黏聚力与压缩模量相关性显著,黏聚力与内摩擦角相关关系不明显;含水率、孔隙比与黏聚力之间具有中等相关性,与压缩模量相关性不明显。
(3)合肥二级阶地晚更新世黏土层工程性质差异性较小,故本研究对缺少勘探孔的各物理力学参数的选用具有一定的参考和借鉴意义。
