火箭发动机超声速过膨胀射流气动噪声特性研究
2020-10-12程修妍荣吉利阿尼苏范博超张博涵
程修妍,荣吉利,阿尼苏,范博超,张博涵
(1. 北京理工大学宇航学院,北京 100081;2. 西安航天动力技术研究所, 西安 710025; 3. 北京强度环境研究所,北京 100076)
0 引 言
运载火箭在发射段会产生强烈的射流噪声[1],尤其在点火升空过程中,近场声压级可达170 dB[2]。强烈的噪声一方面通过透射进入整流罩内部[3],对卫星等有效载荷造成影响,另一方面引起结构振动,对精密仪器造成干扰。因此,研究超声速射流形态、噪声源特点和噪声产生机理,并准确预测发动机气动噪声,对发射场降噪设计有着重要意义。
自20世纪60年代Lighthill[4]创立声类比理论,到Fowcs和Hawkings[5]建立描述任意运动固体边界发声问题的FW-H方程以来,气动声学不断发展,并逐渐应用于工程中。射流湍流边界层拟序结构的发现[6],让人们对射流噪声声源的构成有了更深入的理解。Tam和Chen[7]首次以不稳定波模型的形式对自由剪切流中的大湍流形态进行了统计描述,此后,Tam不断完善不稳定波模型,并提出了射流噪声的两声源模型[8],据此建立了射流噪声相似谱[9],并能较好地吻合已有的实验数据。
高温高速射流的实验成本较高且难以观测,计算技术的发展使得高温高速射流的模拟研究得以推进。李国良等[10]采用RANS结合SST模型对马赫数2.5的发动机燃气扩散及底部流场开展了研究,通过与实验数据的对比检验数值方法的可靠性。陈劲松等[11]结合伽辽金有限元及FW-H方法模拟了单喷管火箭自由喷流,认为卷吸涡的驱动作用、激波扰动及强湍流脉动是产生强湍流噪声的原因,但未对噪声频率特点进行解析。Nakano等[12]和Nonomura等[13]采用LES计算了温度比分别为1.0、2.7和4.0、马赫数为2.0的射流流动及噪声频谱,研究表明随着温度比增大,射流剪切层更多地向射流内部发展,势流核心更短,马赫波辐射角度增大。但其研究对象为完全膨胀射流,与地面环境下的过膨胀射流状态有差别,且最高温度比4.0低于新型运载火箭发动机温度需求,参考价值有限。Cacqueray等[14]采用LES对出口温度360 K、马赫数为3.30的过膨胀射流进行了研究,通过沿剪切层轴向速度脉动的表征研究了射流声源,但未考虑高温对射流噪声的影响。
发动机喷管型面一般设计为完全膨胀状态。但在地面试车或点火起飞过程中,由于地面环境压强大于火箭发动机出口压强,射流处于过膨胀状态。运载火箭发动机喉部总温可达3800 K[15],因此,有必要研究高温高速射流在过膨胀状态下的流动及气动噪声特性。
本文基于LES计算温度比分别为1.0、6.7和12.7的超声速过膨胀射流的非稳态流动,通过FW-H方程计算不同位置噪声源的远场声辐射指向性和声压级-频率分布,结合射流湍流形态分析声源组成及噪声产生机理,为地面试车或起飞状态下的声振环境设计提供参考。
1 模型与计算
1.1 计算方法
本文采用LES对超声速过膨胀射流的流场进行数值模拟,通过状态方程和Smagorinsky模型[16]对亚网格尺度项进行模化处理,此处不再赘述。在计算获取稳定的非稳态流场后,通过FW-H方程计算射流噪声在远场的传播。
Ffowcs Williams和Hawkings基于Curle的工作,采用广义函数法,给出了考虑任意运动固体边界发声的FW-H方程[4]:
(1)
式中:c0为声速,p为压强,t为时间,ρ为密度,Tij为Lighthill应力张量,H(f)为Heaviside函数,δ(f)为Kronecker函数,ui为xi方向的流体速度分量,un为积分面的法向流体速度分量,vi为xi方向的边界面速度分量,vn为边界面法向速度分量。其右端第一项为Lighthill声源项,是湍流运动引起的四极子声源;右端第二项表示表面压力脉动引起的偶极子声源;右端第三项表示表面加速度引起的单极子声源。
1.2 计算模型
数值计算对象为出口马赫数Me约为3.7的超声速射流,其出口直径为D(约为0.12 m)。根据文献[17]中给出的经验公式:
(2)
(3)
预测其层流核心长度Lc约为17D,超声速长度LS约为53D。而射流有效长度LA≈5Lc,约为85D。为了避免出口边界条件对计算结果的影响,选取轴向计算域长度为180D,径向直径为100D,射流计算域尺寸及边界条件如图1所示。
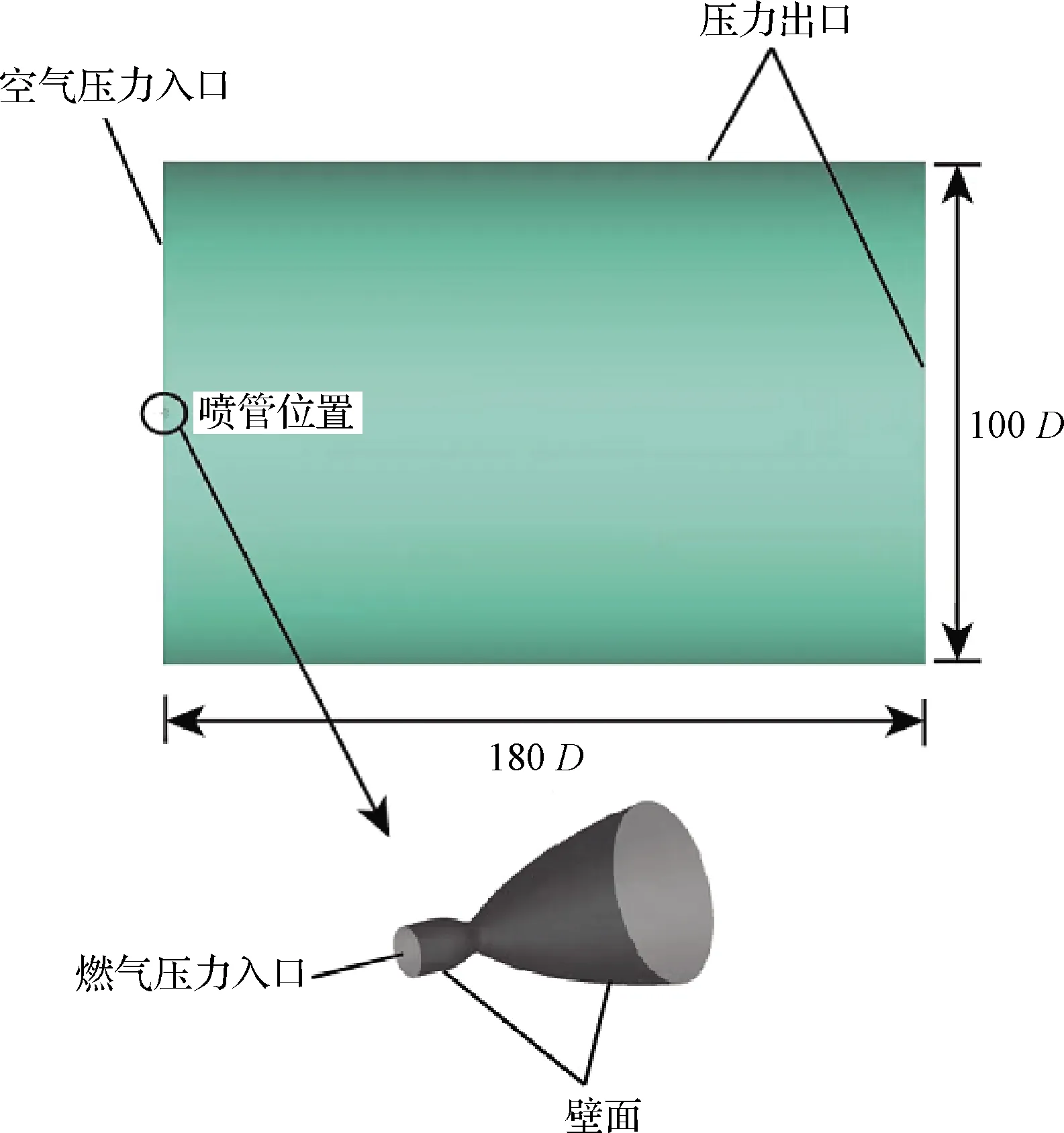
图1 射流计算域尺寸及边界条件Fig.1 Size and boundary conditions of jet calculation domain
给定喷管燃气入口为压力入口边界,总温分别为300 K、2000 K和3810 K(环境温度300 K,温度比分别为1.0、6.7和12.7),总压17.7 MPa;左侧空气边界为压力入口边界,其余出口为压力出口,压强为大气压。在壁面上采用绝热、无滑移壁面条件。
1.3 网格划分
采用结构化网格对计算域进行了离散。网格划分细节如图2和图3所示,喷管入口处、壁面附近对网格进行了加密。计算模型共包括六面体网格484万,最小网格尺寸为0.4 mm。根据网格尺寸和射流速度,将非稳态计算时间步长设定为Δt=2.5×10-6s。为避免初场对非稳态流场计算结果的影响,在非稳态计算满足Uj·t>2xmax,即8000个时间步后开始进行声学计算。
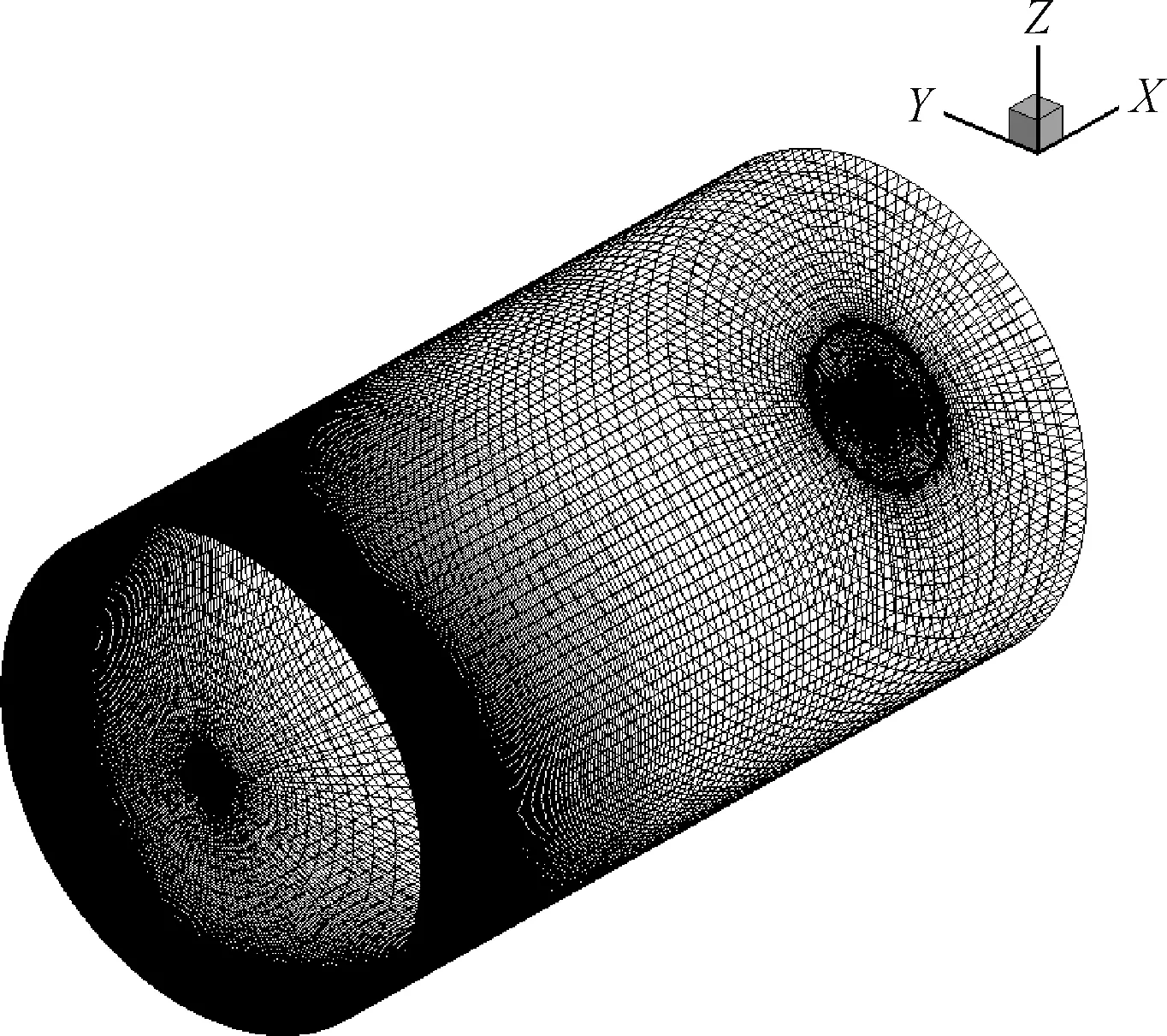
图2 计算域整体网格划分Fig.2 Grid generation in computational domain
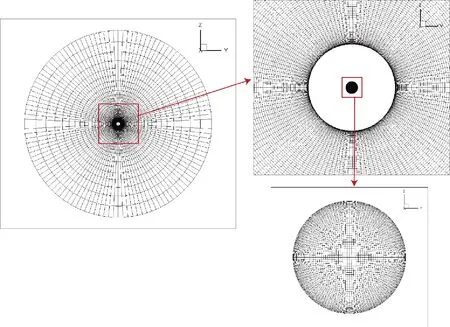
图3 空气入口及燃气入口网格划分细节Fig.3 Grid details of air inlet and gas inlet
2 流场分析
2.1 轴线分布特点
各工况下轴线上的压强、速度、温度、马赫数分布如图4所示,压强和马赫数分布几乎一致,而速度和温度分布影响较大。轴线上速度呈周期性波动,波动幅度随燃烧室温度的增加而增大,随后逐渐衰减。轴线上温度从喉部开始迅速降低,随后周期性震荡,最后逐渐接近环境温度。虽然不同温度比下马赫数分布几乎相同,但仍可以观察到超声速长度的区别。在3810 K时超声速长度约为20.3D,2000 K对时约为22.5D,300 K时约为23.9D,随着射流温度的升高,燃气与周围空气的温差增大,增加了气体间的换热效率,且高温下燃气密度更低,在燃气与周围静止空气掺混过程中速度损失更快,导致了超声速长度降低。
2.2 过膨胀射流特点
图5为温度比12.7时,喷管出口截面中心线的物理量沿径向的无量纲化分布情况。各参数在中心轴线两侧呈对称分布,由于边界层影响,壁面速度为零,向中心处迅速增大,在距离轴线0.48D的范围内,速度保持轴线速度的90%以上,速度分布较为均匀;压强在边界处达到最大值,由于燃气的膨胀,压强向中心迅速降低,中心处压强约为最大压强的15%;温度在边界处达到最大值,向中心迅速降低,在距离轴线0.48D的范围内,温度约为最大温度的40%~55%。
喷管出口压强远低于环境压强,导致射流处于过膨胀状态。图6为轴对称截面出口局部速度分布云图。在压差作用下,自由边界层向中心轴线收缩,高速射流在出口处向轴线偏转,产生了向内的斜激波,斜激波的存在导致气体压强增大,温度升高,在距离喉部约3D的位置形成了第一个马赫盘;随后燃气膨胀,速度方向外扩,中心温度降低;当膨胀波到达燃气射流边界层时,射流再次向内反射形成压缩波;压缩波相遇后在约6D的位置形成了第二个马赫盘。在这之后,由于大气与燃气之间湍流剪切层的形成,破坏了边界层的规律性,导致斜激波的形态发生了改变,进而影响了马赫盘位置和完整性。
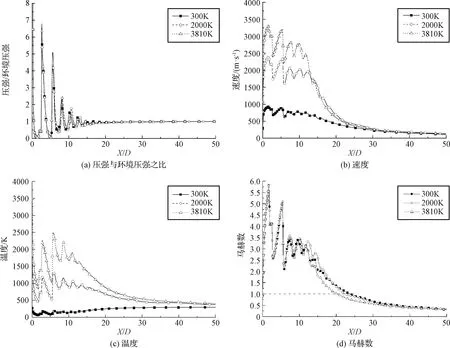
图4 中心轴线物理量分布Fig.4 Physical quantity distribution of central axis
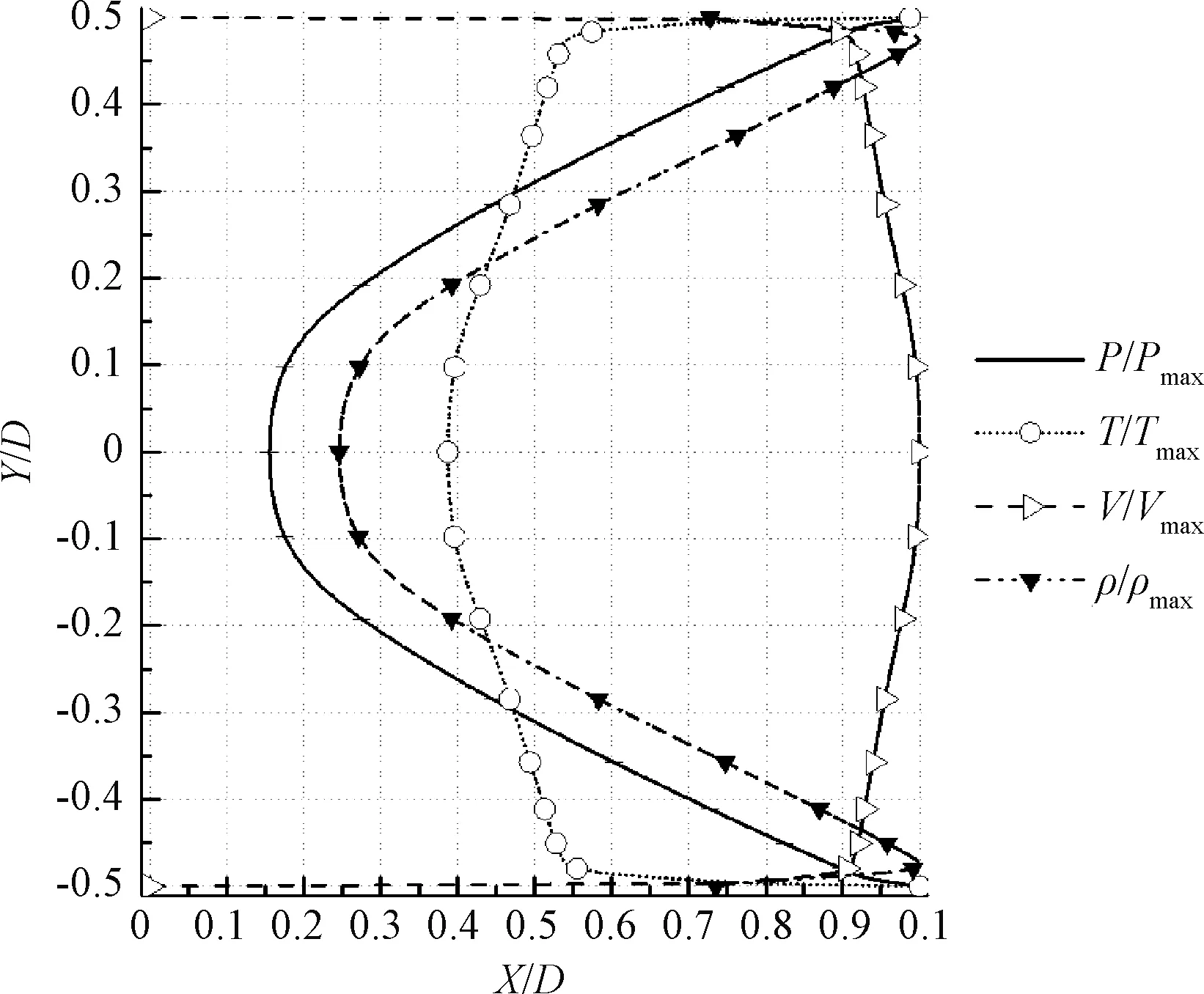
图5 喷管出口无量纲参数分布Fig.5 Dimensionless parameter distribution of nozzle exit

图6 轴对称截面速度分布(局部)Fig.6 Velocity distribution of axisymmetric section (local)
2.3 近场声压及湍流
非稳态流场的声压,即压力脉动定义为:
p′=p-pstatistics
(4)
式中:p为瞬态压强,pstatistics为时均压强。将三个工况下轴对称截面上的声压和涡量匹配,如图7所示,射流涡结构主要位于轴向6D~50D、径向10D范围内。从6D开始逐渐从剪切层产生小尺度湍流,随射流向下游发展,剪切层增厚,湍流尺度逐渐增大,形状更加不规则。随温度比增加,湍流在径向的分布范围更宽。
结合声压分布可见,超声速射流的湍流边缘产生了向下游传播的马赫波,但向上游传递的效应不明显。随着射流向下游发展,湍流尺度增大,马赫波波长增加。随温度比升高,马赫波幅值增加,主导马赫波的传播方向角增大,在温度比1.0时传播方向约为50°,温度比6.7时约为58°,温度比12.7时约为68°。这一方面是由于大温度比使射流与空气之间形成了更大的温差,导致剪切层能量交换更为剧烈,射流剪切层增厚,湍流度增强,改变了声源分布位置;另一方面是高温使燃气射流加速,并在向前运动的过程中通过剪切层带动周围空气向下游运动,导致主导马赫波的传播向上游方向偏转。
3 远场噪声分析
3.1 声源分解
为了分析不同位置声源的远场辐射特点,对声源进行分解。如图9所示,采用渐扩形圆筒面S1涵盖声源较为剧烈的区域,其具体尺寸特征为:起始位置距离喷管出口2D,起始位置半径2D,轴向长度为50D,终止半径为10D;采用圆柱面S2涵盖下游噪声源,长度为50D,半径10D。
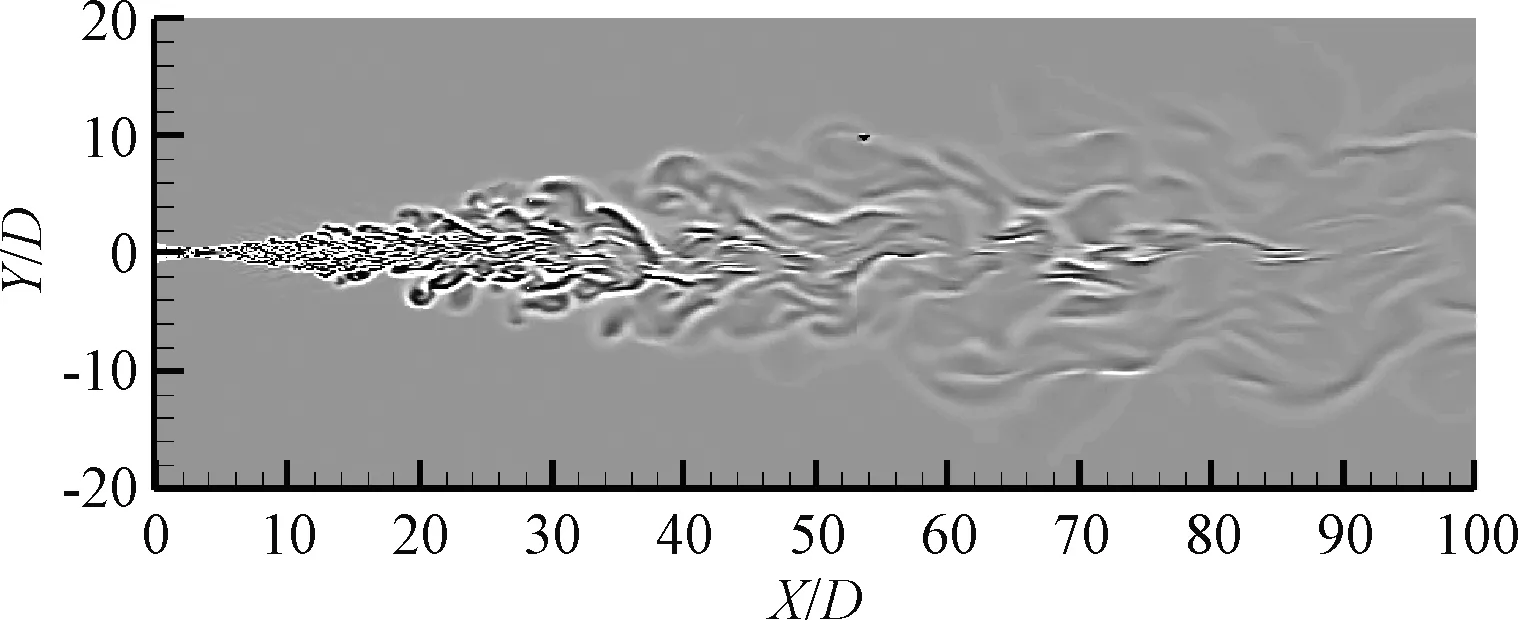
图8 轴线对称截面上的Lighthill声源项分布Fig.8 Distribution of Lighthill sound source term on axisymmetric section
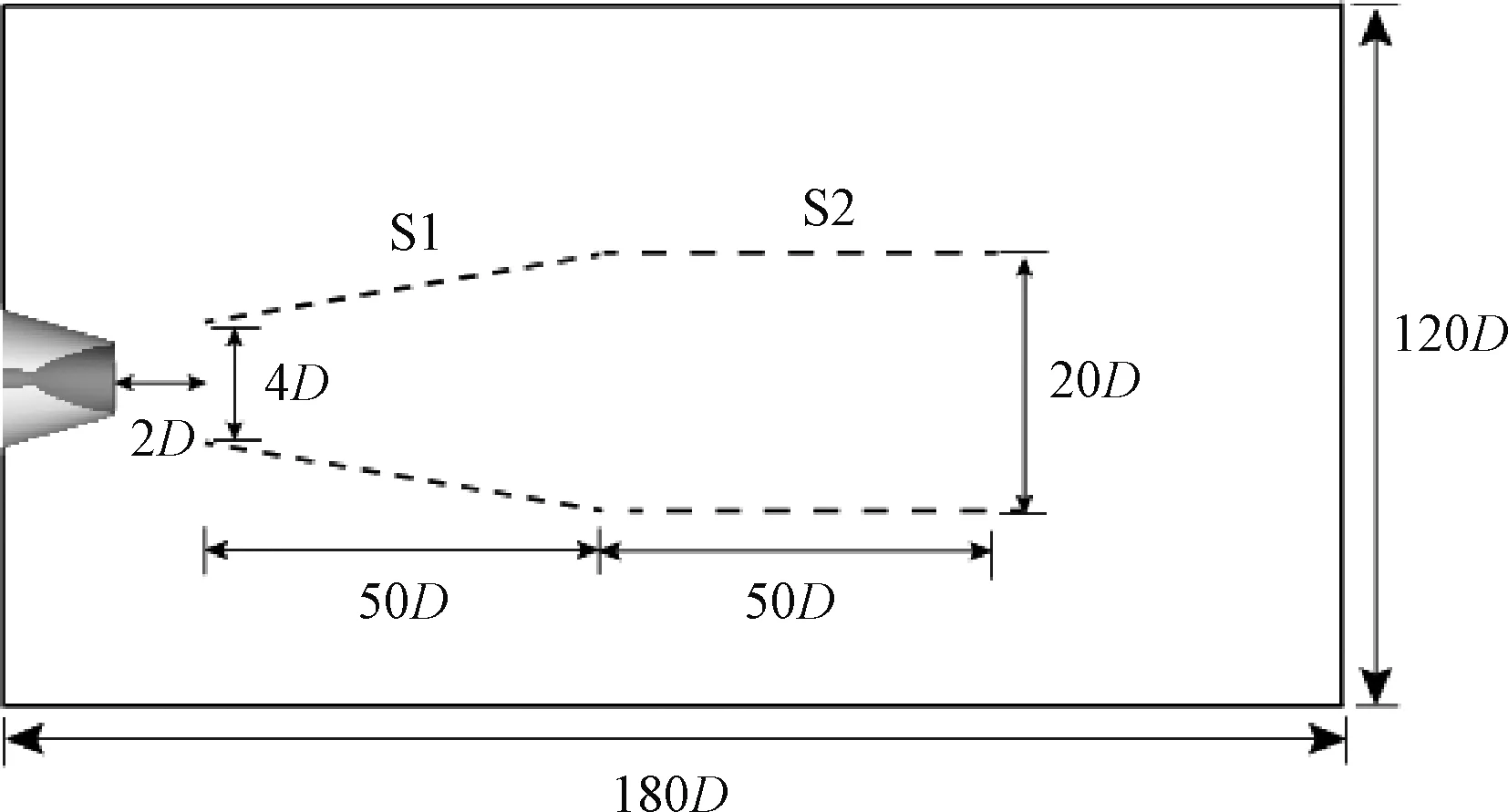
图9 声源面位置示意图Fig.9 Schematic diagram of sound source surface location
3.2 声源位置与噪声指向性
以入口温度比为12.7的工况为研究对象,通过FW-H方程计算远场声辐射情况。在声源控制面外部距离喷管喉部R=120D设置一组半圆形观测点,总声压级随角度变化的曲线如图10所示。S1+S2和S1的远场辐射总声压级在30°~180°范围内几乎完全相同,而在0°~20°范围内,S2辐射的总声压级最大。结合图7,S1中主要为中小尺度湍流,噪声以马赫波形式向外传播,而S2中主要分布大尺度湍流,无明显马赫波。因此可以得出,近场中小尺度湍流噪声源主导了30°~180°噪声,而下游大尺度湍流噪声源主导了下游方向噪声。
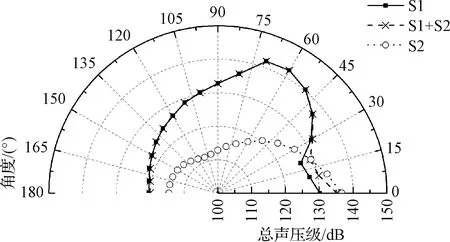
图10 不同声源总声压级随角度的变化Fig.10 Overall sound pressure level with angles by different noise source
3.3 入口温度比对声辐射指向性的影响
以三种工况的非稳态流场的S1声源为研究对象,通过FW-H方程计算远场距离喷口80D处的声辐射情况,如图11所示,射流温度越高,噪声越向轴线外侧辐射,这与文献[18]中的研究结论一致。在温度为300 K时,最大总声压级的辐射角为40°,在2000 K时为50°,在3810 K时为60°,声压级约147 dB,结合图7,高温导致马赫波传播角度增大,进而造成了S1声源远场总声压级辐射角增大,说明S1内辐射指向性由马赫波传播方向决定。
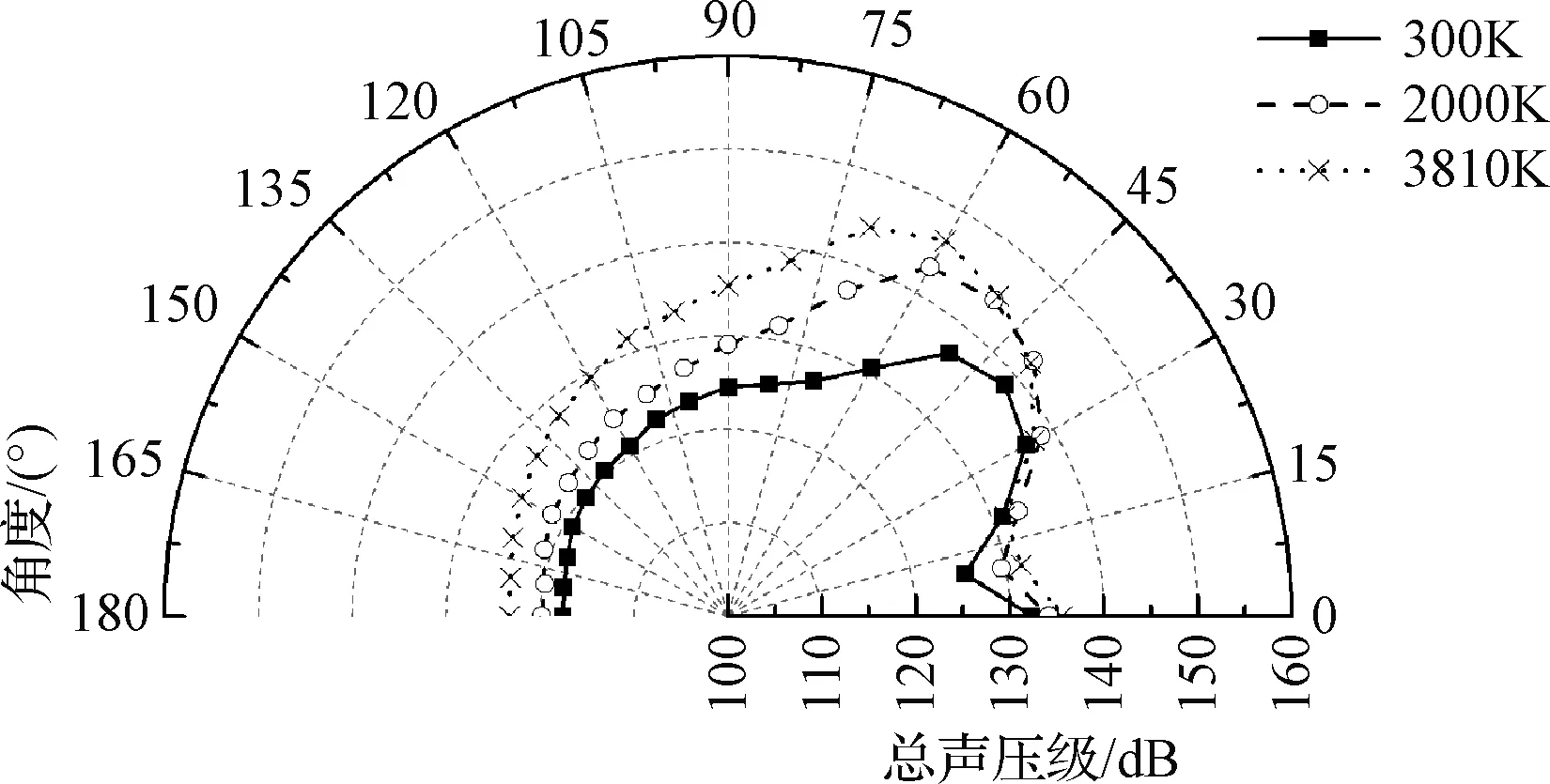
图11 不同温度下远场声压级随角度的变化Fig.11 Overall sound pressure level with angles in different temperature
3.4 声辐射频率分布
射流噪声主要包含湍流混合噪声和宽频激波噪声[7]。湍流混合噪声与射流中的湍流形态有关,而宽频激波噪声是不稳定波与激波晶胞结构相互作用引起的。为排除流场声速对频率分布的影响,将频率采用修正的Strouhal数无量纲化处理[19]:
(5)
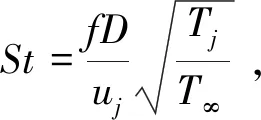
随着观测角度的增大,S2区域大尺度湍流辐射噪声对总声压级贡献越来越小,而S1区域内声源的辐射占比增加,观察到图12(b)-(c)中声压级峰值频率随角度的增加而增大,说明马赫波辐射噪声主要分布于中高频范围,在30°方向,大尺度湍流噪声和马赫波辐射噪声混合形成了30°方向的湍流混合噪声,峰值频率约为St=0.04,在60°方向的峰值频率约为St=0.15。
在90°和120°方向,流场无明显的马赫波辐射,且无大尺度湍流,此范围内主要是湍流辐射的背景噪声。然而,图12(d)和(e)中可见在St=0.25附近较宽的范围内声压级较大,这主要由不稳定波在过膨胀射流的周期激波单元中散射形成的宽频激波噪声所引起。
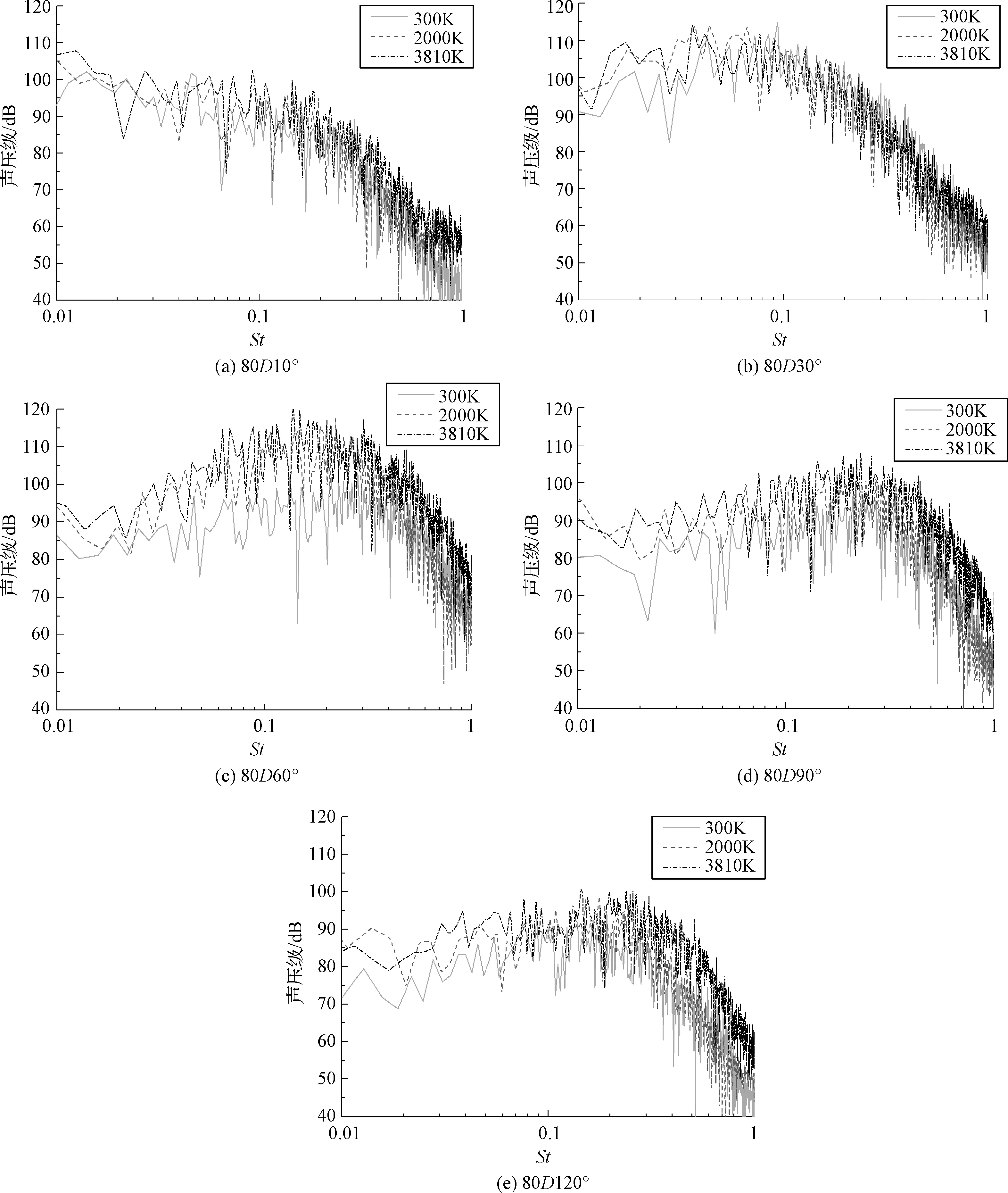
图12 不同角度观测点的声压级-频率分布Fig.12 Sound pressure level with frequency at different angles
4 结 论
本文对不同温度比的火箭发动机超声速过膨胀射流流动和声辐射进行了研究,综合分析了湍流形态与噪声组成的关系,研究结果表明:
1) 射流的过膨胀导致了出口中心压强和温度迅速降低,射流边界层向轴线收缩;温度比不影响流场的周期性规律,但高温缩短了燃气的超声速长度,加剧了射流剪切层发展。
2)近场噪声源由射流剪切层产生的湍流构成,并以马赫波形式在大角度范围辐射中高频噪声;下游噪声源由大尺度湍流构成,向下游小角度范围辐射低频噪声,共同组成了湍流混合噪声。
3)声辐射指向性由马赫波传播方向决定,随着温度比的升高,马赫波幅值增加、传播角度增大,导致声辐射强度、辐射角度增大,在温度比12.7时最大声压辐射角约为60°,80D处声压级达147 dB。
