基于多元线性回归与时间序列的风力发电中风速捕捉综合预测研究
2020-10-10董浩文张倩颖陈兆艺赵益钱禹清
董浩文 张倩颖 陈兆艺 赵益 钱禹清

摘要:在风力发电中的叶尖速比跟踪风能中,需要时刻掌握风速的动态,但由于风机捕捉风速后再调整的滞后性,对风速进行短期预测并提前调整至预定状态,事后加以微调就显得尤为重要。鉴于此,对基于时间序列预测和多元线性回归组合再进行蒙特卡罗实时加权寻找最适宜风速的预测方法进行研究,综合两种方法利弊,适时调整权重,增强预测稳健性。
关键词:时间序列;多元线性回归;蒙特卡罗模拟;预测捕捉
0 引言
随着经济和科技日益发展,风力发电已经成为清洁能源不可或缺的一个组成部分。2018年,全球风电新增装机容量超过60 GW,并在其后4年内稳定增长;2020年,全球新增风电装机达到80 GW,机遇与挑战并存。对于风力发电而言,风机的最大风能跟踪(MPPT)控制显得尤为重要,目前控制策略中的叶尖速比控制方法由于每台风机最优叶尖速比不同,故对风机依赖较强,需要实时测量风速,而实际风速测量误差较大,因而就需要相应预测在短时间内风速的变化,让风机适当提前调整运行特性,以提高控制系统的可靠性。
考虑到风速具有一定的随机性和周期性,与当时空气的温度、湿度、气压等均有着密不可分的联系,因此将数据分为训练组和实验组,采用能预测具有一定周期的时间序列和能够综合考量温度、湿度等因素的多元线性回归预测进行组合,再根据实时风速,进行蒙特卡罗模拟加权修正,进一步提高预测的稳健性。
1 实验方法及思路
本文采用时间序列中含有季节成分的SARIMA(p,d,q)(P,D,Q)(m周期)的模型进行时间序列建模:
1-
?iLi1-
?iLmi(1-L)d(1-Lm)Dyt=
α0+1+
θiLi1+
ΘiLmiεt (1)
式中:L为滞后算子;m为周期;p为AR模型阶数;d为非季节差分数;q为MA模型阶数;P为含季节成分AR模型阶数;D为含季节成分差分数;Q为含季节成分MA模型阶数;θ,Θ,?均为模型预测结果参数;α0为常数项;εt为残差扰动项。
结合贝叶斯和赤池信息准则选择模型,并结合残差ACF和PACF综合确定模型参数,同时最后用Q检验白噪声序列来验证模型,转而建立另一回归预测模型,先处理气压、降水量等数据,再由这些因素对风速进行一个最小二乘线性(OLS)+稳健标准误回归进行建模预测风速,模型如下:
yi=0+jxij+εi (2)
式中:yi为风速因变量;xij为降水、温度等因素,自变量;εi为扰动项;0,j均为回归系数。
将两种方法的预测结果与其实际结果进行对照,实时进行蒙特卡罗模拟,寻找与实时风速最契合的权重,紧接着应用到下面的风速预测中,具体应用见实例。
2 应用实例
2.1 时间序列
以具有一定利用价值的内蒙古呼和浩特风速为例,从中國气象网采集2020年7月15日到7月25日每小时气压、风向角、湿度等因素共计264个样本进行分析。
2.1.1 数据分析及模型的建立
对数据进行简单分析,发现其具有明显的时间成分,即在某个时间段风速变化明显,可以将其类比为季节成分,采用具有季节性的ARIMA模型即SARIMA(p,d,q)(P,D,Q)周期为24的模型进行预测,充分利用SPSS专家建模器[1]拟合出最为贴切的预测模型并进行验证分析,预测出26日前5小时在95的置信区间预测的中间值,如图1所示。
预测值呈现先升后降的趋势,符合风速的一般变化规律,得出预测模型为SARIMA(1,0,0)(0,1,0)(周期m为24),显然,由模型可以看出风速中的季节成分并不平稳,需要进行一阶差分,定义εt为残差,L为滞后算子,则有:
Liyt=yt-i (3)
(1-?1L)(1-?1L24)(1-L24)yt=α0+εt (4)
其中SARIMA模型中的AR模型延迟1系数为0.321。
2.1.2 模型参数及残差的验证
由模型具体拟合中给出的残差ACF和PACF值能够得出在一阶显著异于0且一阶后即已经截尾,结合赤池信息准则(AIC)和贝叶斯准则(BIC)[2]选择模型,使p和q在某一值时,复杂度与数据解释能力之间存在着最佳平衡,由SPSS中给出的BIC值为0.538以及AIC等值综合验证模型中p值为1。同时由数据分析可知风速并不平稳,为了使风速变化的速率相对平稳些,进行了一阶季节差分,使模型变化速率更加平稳,即D值为1。另在模型预测之前,假设的残差为白噪声序列:
E(xt)=E(xt-s)=0 (5)
Var(xt)=Var(xt-s)=σ2 (6)
Cov(xt,xt-s)=0(s≠0) (7)
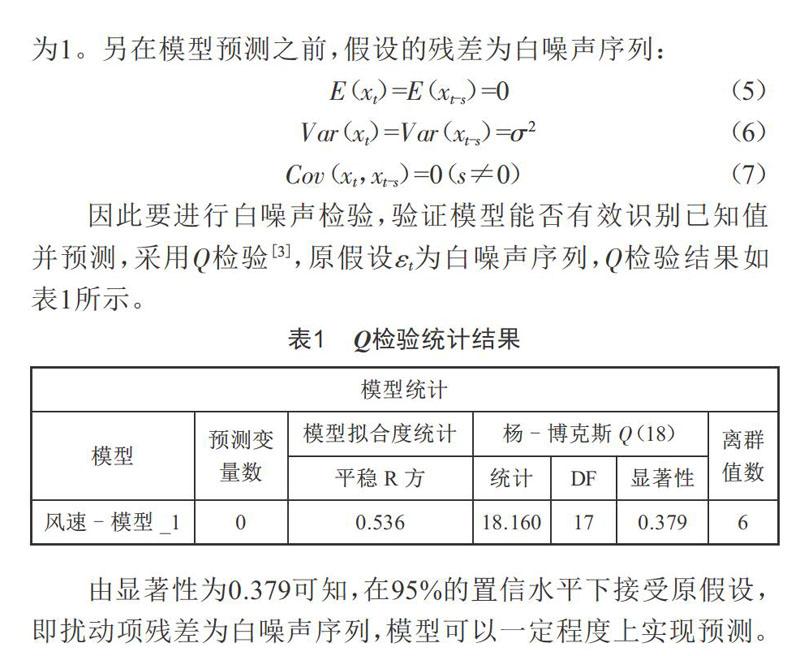
因此要进行白噪声检验,验证模型能否有效识别已知值并预测,采用Q检验[3],原假设εt为白噪声序列,Q检验结果如表1所示。
由显著性为0.379可知,在95%的置信水平下接受原假设,即扰动项残差为白噪声序列,模型可以一定程度上实现预测。
2.2 多元线性回归
考虑到风速由多种因素影响,为了在短时间更精确预测出风速,还需要将当时的天气等因素综合考虑在内,才能高效预测出风速,为此采用多元线性回归的方法。
2.2.1 数据预选取与处理
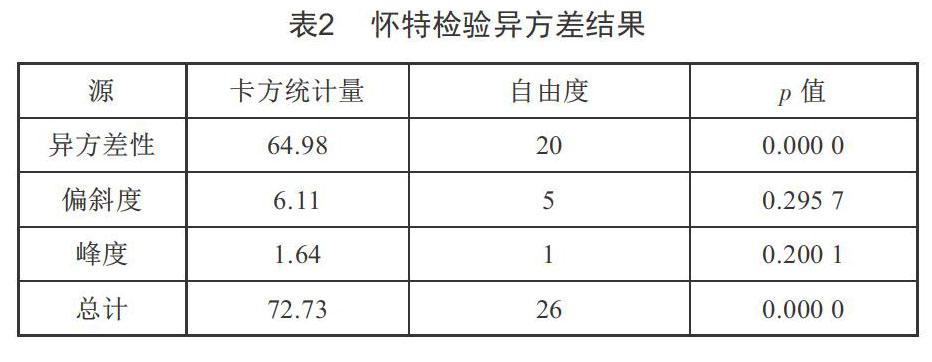
首先对整体数据的扰动项进行怀特检验异方差,检验结果如表2所示。
显然拒绝原假设,即数据的扰动项存在异方差,因此为减弱数据的异方差,使变量渐进为正态分布并更具有现实意义,将因变量风速进行取对数处理,以风速对数为因变量,依次取气压、风向角、温度、相对湿度、降水量为自变量。
2.2.2 模型选择建立与解释
考虑预测分为解释回归和预测回归,对风速的捕捉预测偏预测回归,因此对多重共线性的影响可以不必理会,以防数据缺失加强内生性。但不能忽视回归模型中的扰动项存在异方差的问题,因为一旦扰动项存在异方差,势必造成回归系数不是最优无偏解,因此为了使扰动项趋于球形扰动项[4],构造t统计量=回归系数/标准误,进而进行最小二乘线性(OLS)+稳健标准误回归,消除扰动项异方差带来的影响。具体回归系数如表3所示。
得出回归预测模型如下:
ln(风速)=-0.013气压+0.001风角+0.009温度-
0.005湿度-0.044降水量+11.677(8)
由该回归模型不难看出,在95%的置信水平下,当气压每增加1个单位,风速大约相对减少1.3%,风角每增加1°,风速相对增加1%,温度、相对湿度降水量等依次类推。
3 蒙特卡羅模拟加权简述
因蒙特卡洛模拟[5]需具体应用在风机上进行实时模拟,此处简述其思路:得到预测值后与其实际值进行对比,并进行实时模拟加权,此处模拟次数取1 000次为宜,次数过多,模拟时间加长,反而起不到预测的效果,实时得到权重后将权重应用到下面的预测加权中,后面再进行实时调整修正,提高预测准确性,此处不再赘述。
4 结语
风速捕捉预测在实现最大风能跟踪策略研究上具有深远意义,本文结合了多元线性回归中消除异方差的一种稳健回归和时间序列中的考虑季节因素的模型综合蒙特卡罗模拟加权捕捉风速,从现实角度,可以有效实现风机风速的预测,让风机提前进入预备状态。由于考虑加权并实时修正,该方法避免了单种方法的不确定性和偶然性,且因为考虑了外在因素如气温、降水量等的影响,同时也考虑了内在因素如风机风速自身的时间变化趋势等,方便了实际检测应用。
[参考文献]
[1] 胡碧波,傅克本,许亮亮,等.应用ARIMA模型预测结核病发病率研究[J].预防医学,2018,30(10):1011-1015.
[2] 杨贵军,孟杰,王双喜.基于赤池信息准则的分类回归决策树剪枝算法[J].计算机应用,2014,34(S2):147-150.
[3] 尹温硕,陶顺,赵蕾.基于ARMA模型的电压RMS值预测[J].电力工程技术,2018,37(5):20-25.
[4] 陈晓龙,杨志颖,李永丽,等.基于MPPT梯形电压扰动的直流微电网新型孤岛检测方法[J/OL].电网技术:1-11(2020-
07-29)[2020-07-30].https://kns.cnki.net/KCMS/detail/
11.2410.TM.20200729.1429.006.html.
[5] 杨欢,邹斌.含相关性随机变量的概率最优潮流问题的蒙特卡罗模拟方法[J].电力系统保护与控制,2012,40(19):110-115.
收稿日期:2020-07-31
作者简介:董浩文(2000—),男,江苏扬州人,研究方向:电力系统检修及分析。
