小型山地履带拖拉机爬坡越障性能分析与试验

潘冠廷 杨福增 孙景彬 刘志杰

(1.西北农林科技大学机械与电子工程学院， 陕西杨凌 712100； 2.农业农村部北方农业装备科学观测实验站， 陕西杨凌 712100)

0 引言

我国地形多样、地貌复杂，丘陵和山地占国土面积的近70%[1]。丘陵、山地的耕、种、收综合机械化率仅有15%左右，远低于平原地区超过70%的水平。在制约农业机械化发展的众多因素中，农业机械的动力问题极为关键，因此对于丘陵山地动力机械及其性能的研究已成为农机领域的研究热点之一。

目前，针对山地拖拉机的研究主要集中在样机研发及结构改进[1-2]、多体动力学建模与仿真[3-4]、自动化与智能化[5]等方面，尤其在机械性能分析与拖拉机结构改进方面的研究更为广泛。为了提高拖拉机坡地作业的稳定性，20世纪90年代有学者通过改进中小型四轮拖拉机底盘来实现车身姿态的调整[6-7]。目前，大量研究主要围绕如何控制拖拉机姿态以提高其在山地作业的稳定性及抗翻倾能力[8-11]，有关山地拖拉机牵引附着性能[12]、转向性[13]、机体及农具对山地的自适应[5]等方面的研究也在不断深入。但是，目前针对山地拖拉机越障性能的研究相对较少，主要集中在履带式拖拉机平地越障及轮式拖拉机山地等高线越障方面[14-18]，且大多为仿真分析，较少有实车田间试验研究。

丘陵山区田间的台阶、砖头、石块、田埂等障碍物极为常见，这些障碍物是降低山地拖拉机行驶稳定性的重要因素之一，严重时会使其无法跨越，引发侧滑甚至翻倾等安全问题。据有关资料，因翻倾引发的农用拖拉机安全事故致死率超过50%[19]。因此，开展山地履带拖拉机爬坡时的越障性能研究非常必要。

本团队自主研发了小型山地履带拖拉机(以下简称山地拖拉机)[20-21]。对该机已经进行了多项性能研究，包括牵引附着性能、爬坡性能、坡地行驶稳定性、坡地转向性能等[22-26]，但针对该机的越障性能研究并未涉及。

本文从运动学和动力学角度分析山地拖拉机的爬坡越障过程，建立最大越障高度与坡度角、越障速度、质心位置之间的数学模型，并以最大越障高度评价其坡地越障性能；仿真分析和实车田间试验相结合，对该数学模型的有效性进行验证，为山地拖拉机的结构优化、性能提升等提供理论支持。

1 爬坡越障性能分析与数学模型构建

1.1 越障过程描述

在台阶、砖头、石块、田埂等各类农田障碍物中，台阶对山地拖拉机爬坡带来的失稳和安全问题最为严重，故其跨越台阶的能力最能体现山地拖拉机爬坡越障性能。该过程共分为3个阶段[25,27]，如图1所示。

图1 山地拖拉机爬坡越障过程示意图Fig.1 Schematics of obstacle negotiation process when climbing up slope

第1阶段为前端接触阶段，如图1a所示。山地拖拉机在坡地上低速前进，履带前端与台阶边缘接触，然后整机绕最后一个支重轮发生逆时针转动，同时整机沿台阶边缘向前移动。

第2阶段为越障阶段，如图1b所示。山地拖拉机继续向前行驶，履带接地段接触台阶上部，直到重力作用线与台阶边缘重合。

第3阶段为越障完成阶段，如图1c所示。当重力作用线超过台阶边缘的瞬间，在惯性作用下拖拉机与台阶下端脱离，完成越障过程。

1.2 越障运动学及动力学模型

山地拖拉机能否顺利完成越障，关键在第2阶段，此阶段某一时刻的运动状态如图2所示，履带接地段与坡道平面的夹角β急剧增大，山地拖拉机极有可能发生纵向翻倾。为分析山地拖拉机的爬坡越障性能，构建最大越障高度的数学模型，需对其越障第2阶段进行运动学及动力学分析。

图2 越障第2阶段运动示意图Fig.2 Schematic of obstacle negotiation process in phase Ⅱ

基于履带式拖拉机的行驶特点、工况和相关研究经验[16,28]，本研究做以下假设：

(1)忽略山地拖拉机在越障时质心偏移产生的影响。

(2)山地拖拉机两侧履带运动状态保持一致，即同时接触台阶边缘，两侧履带受力相同。

(3)将台阶视为刚体，不会因为与履带接触而产生破坏和变形。

(4)山地拖拉机在越障过程中始终沿纵向坡道运动，不存在横向摆动。

(5)越障过程中履带始终保持张紧状态，与台阶边缘为线接触。即台阶对于履带接地段的作用力方向始终经过台阶边缘，且方向垂直于履带所在平面。

(6)越障过程中，驱动力在山地拖拉机行驶方向上的分量足够大，足以驱动其完成整个越障过程。

如图2所示，坡地及台阶对山地拖拉机的支撑分别作用于点O和O1，山地拖拉机质心在垂直于履带接地段方向上的投影交OO1的延长线于点A，坡道与台阶边缘相交于点B，过点O做水平线与O1B相交于点C。将山地拖拉机看作刚体，由三角形OACG代替，且OA边与履带重合。

建立坐标系oxy，使x轴始终平行于履带接地段。定义点OICV为该时刻山地拖拉机的速度瞬心，vO、vO1与vCG分别表示该时刻点O、O1与质心CG的速度；α为坡度角，β表示越障过程中的山地拖拉机仰角(履带接地段与坡道之间的夹角)，δ表示vCG与x轴之间的夹角；k表示质心到最后一个支重轮的水平距离(以下简称质心-支重轮距)，h表示质心高度，r表示支重轮半径，H表示障碍物高度。

对三角形OACG进行速度分析，可得

(1)

式中vO——O点速度(即越障速度)，km/h

vt——驱动轮分度圆线速度，km/h

lOICVO——OICV到O的长度，mm

由几何关系可得

(2)

式中lOO1——O到O1的长度，mm

lOICVCG——OICV到CG的长度，mm

故可求得质心CG的速度、法向加速度及切向加速度，为动力学分析提供依据，具体为

(3)

式中vCG——质心CG的速度，m/s

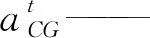
当山地拖拉机的重力作用线与台阶边缘重合时，山地拖拉机完成越障第2阶段，由几何关系可知

(4)

式中γ——三角形OACG中OCG与OA的夹角

lOCG——O到CG的长度，mm

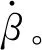
山地拖拉机在越障第2阶段的运动是平面复合运动，可以分解为沿坡地向上的平动和方向为逆时针的转动，其惯性力系可以简化成一个作用在CG上的惯性力FI和一个惯性力偶矩MI。在重力作用线与台阶边缘重合之前，山地拖拉机的受力如图3所示。

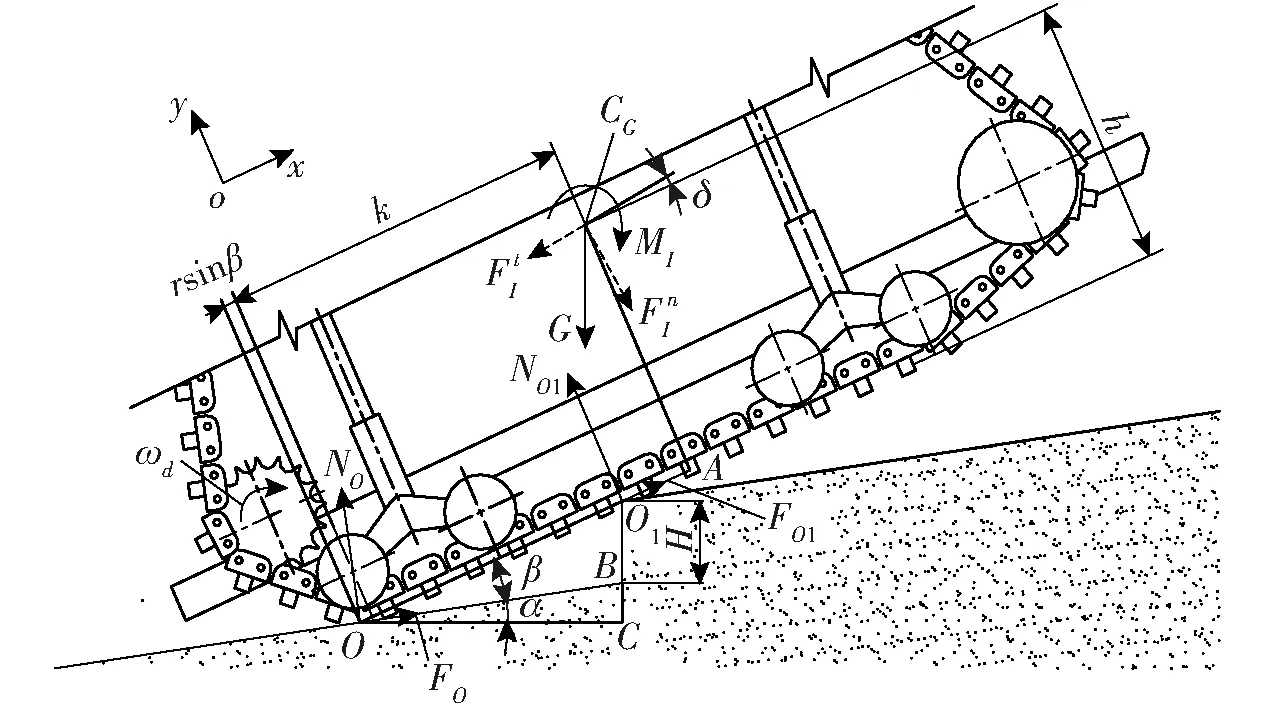
图3 越障第2阶段受力图Fig.3 Force schematic of obstacle negotiation process in phase Ⅱ

作用于拖拉机上的力有重力G、坡地对最后一个支重轮的支持力NO及切向力FO、台阶对履带接地段的支持力NO1及切向力FO1，NO1垂直作用于履带接地段。

对于FI，其在拖拉机质心加速度切线和法线方向上的分量分别为

(5)

m——山地拖拉机质量，kg

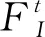
(6)

山地拖拉机行驶时，地面对于履带接地段的切向作用力与对其的支持力成正比[29]。因此，作用于点O和O1上的切向力FO及FO1可表示为

(7)

其中

φ0=φ-f

(8)

式中φ——坡地和履带之间的附着系数

f——地面的变形阻力系数

根据达朗贝尔原理，作用在山地拖拉机上各力在x轴与y轴上的分量组成平衡力系，有

(9)

式中JCG——拖拉机绕质心CG的转动惯量，kg·m2

在山地拖拉机跃上台阶之前，整机有绕点O向坡道下方翻倾的可能，因此对点O求矩，为方便计算，设顺时针为正，逆时针为负。为使整机在越障过程中不发生翻倾，要求作用于山地拖拉机上的外力对点O的合力矩不为负，即

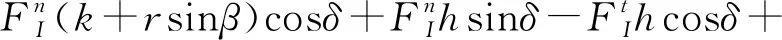
(10)

山地拖拉机的爬坡越障性能主要由最大越障高度评价，用Hmax表示。在地面参数给定的条件下，Hmax越大，表明其越障性能越好。结合式(1)、(2)可得出Hmax的表达式

(11)

β=f(vO,α,k,h)

(12)

将式(12)代入式(11)可得

(13)

式中f′(vO,α,k,h)表示f(vO,α,k,h)的导数。由式(13)可知，Hmax是关于vO、α、k、h的函数。

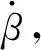
1.3 最大越障高度计算与分析

本文计算分析所用的山地拖拉机主要参数如表1所示[1]。

表1 山地拖拉机主要参数Tab.1 Main parameters of SHCT

对于本实验室研发的山地拖拉机，由于质心位置k与h已知，故vO及α是影响Hmax的主要因素。根据式(11)可计算出该机在不同α及越障速度vO下的Hmax，如图4、5所示。

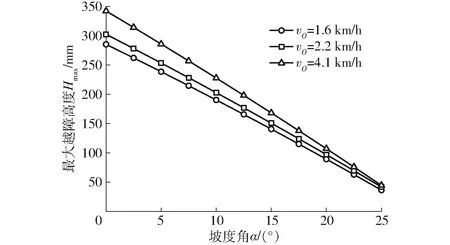
图4 最大越障高度随坡度角的变化曲线Fig.4 Changing curves of maximum obstacle clearance height with slope angle

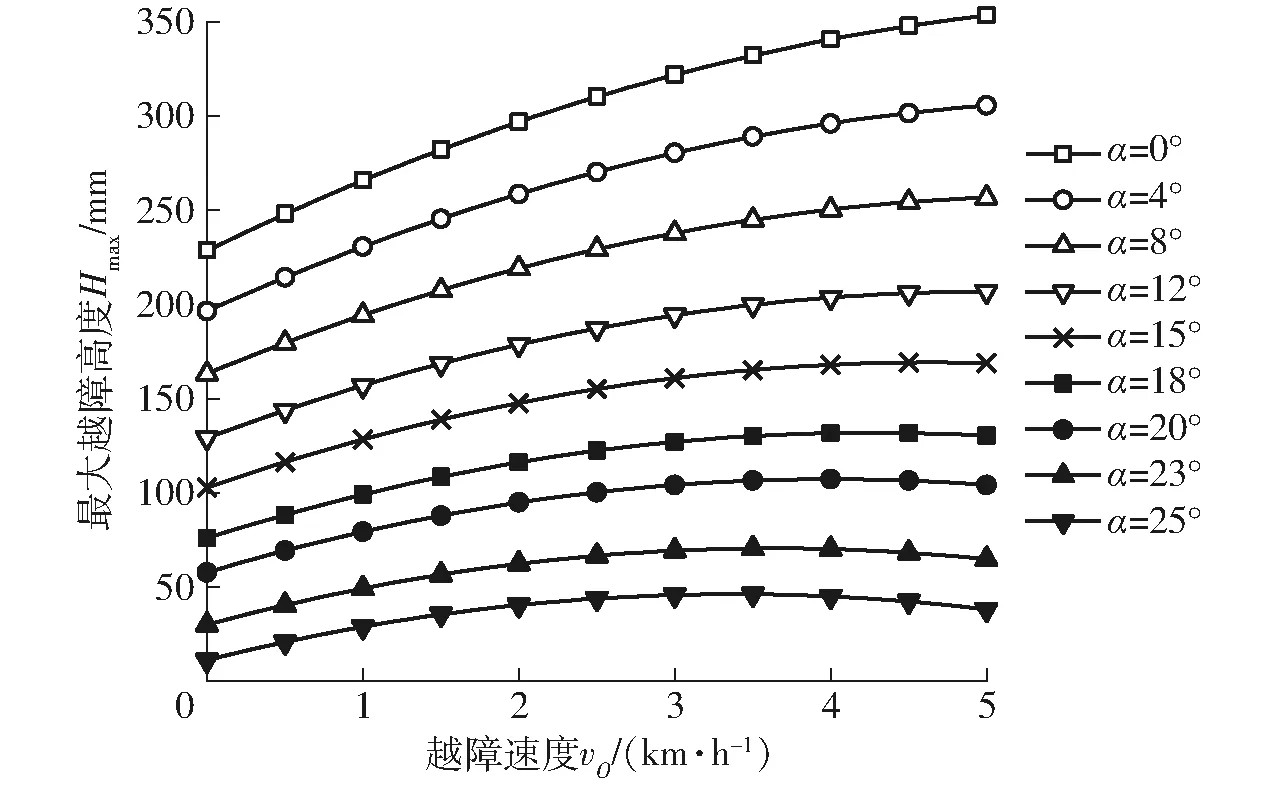
图5 最大越障高度随越障速度的变化曲线Fig.5 Changing curves of maximum obstacle clearance height with tractor speed

由图4可知，随着α的增大，Hmax减小，且3条曲线逐渐靠近，即α越大，Hmax随vO的变化越小。说明坡度角较大时，越障速度对于山地拖拉机的爬坡越障性能影响较小。对图4中的主要数据进行拟合可得到该机在各挡位下的最大越障高度简易计算公式

(14)

图5给出了不同坡度角下的越障速度对Hmax的影响曲线。由该图可直观地看出，当α<15°时，Hmax随越障速度的增大单调递增，呈逐渐上扬的趋势；α≥15°时，Hmax随越障速度的增大呈现先增大后减小的趋势，说明在坡度角较大时，越障速度的增大并不能提高山地拖拉机的越障性能。对图5中的主要数据进行拟合可得到该机在不同坡度角下的最大越障高度简易计算公式

(15)

2 多体动力学仿真试验

2.1 仿真模型的建立

由于前述Hmax的简易计算公式仅仅是针对本团队研发的山地拖拉机，其质心位置为确定值，并不能看出质心位置变化对Hmax的影响趋势。为了使本研究成果更具有普遍性和代表性，还需进一步研究质心位置变化对于Hmax的影响以及各因素对于Hmax影响的显著性。

基于Creo Parametric软件，首先建立山地拖拉机机体3D模型并导入RecurDyn软件的低速履带模块(Track-LM)；其次，按照表2所示参数，构建履带行走系的零部件几何模型[30]；最终构建出可用于多体动力学仿真分析的山地拖拉机虚拟样机模型，如图6所示。

表2 履带行走系及主要零部件参数Tab.2 Main parameters of SHCT mm

图6 山地拖拉机虚拟样机Fig.6 Virtual prototype of SHCT1.履带 2.驱动轮 3.支重轮 4.平衡臂 5.导向轮 6.机体

2.2 正交试验因素及水平

采用正交试验设计方法对影响山地拖拉机坡地最大越障高度的主要因素进行仿真分析。

我国可耕地按照坡度可分为3大类，坡度角在0°～6°之间的为平耕地，坡度角在6°～15°之间的为缓坡耕地，坡度角在15°～25°之间的为陡坡耕地；坡度角大于25°的为非耕作地块。由于大于20°的坡地水土流失严重[31]，不适宜耕作，因此本研究考虑将坡度角α作为因素A并在0°～20°之间设置6个水平；山地履带拖拉机3个前进挡的设计速度分别为1.6、2.2、4.1 km/h，因此考虑将vO作为因素B并以3个前进挡的设计速度作为水平；另外，拖拉机的配重位置不同将导致质心-支重轮距k的变化，不同功率的拖拉机由于体积不同，其质心高度h也有所不同。因此考虑将拖拉机质心位置参数k和h作为因素C和因素D并分别设置3个水平。具体水平设置如表3所示。

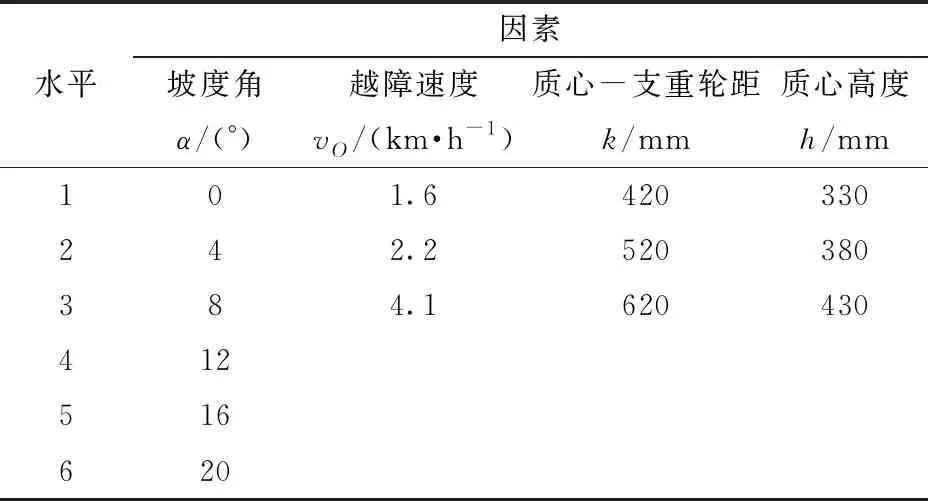
表3 仿真因素及水平Tab.3 Factors and levels of simulation experiment

2.3 正交试验方案及结果分析

根据表3所示因素及水平设计正交试验，并以Hmax作为试验指标，试验方案及结果如表4所示，表中A、B、C、D为因素水平值。表中Ri为第i个因素的极差。为消除因素水平不同对Ri的影响，引入极差折算系数di对Ri进行修正，并用修正后的极差R′i来判定主次因素，其计算公式为

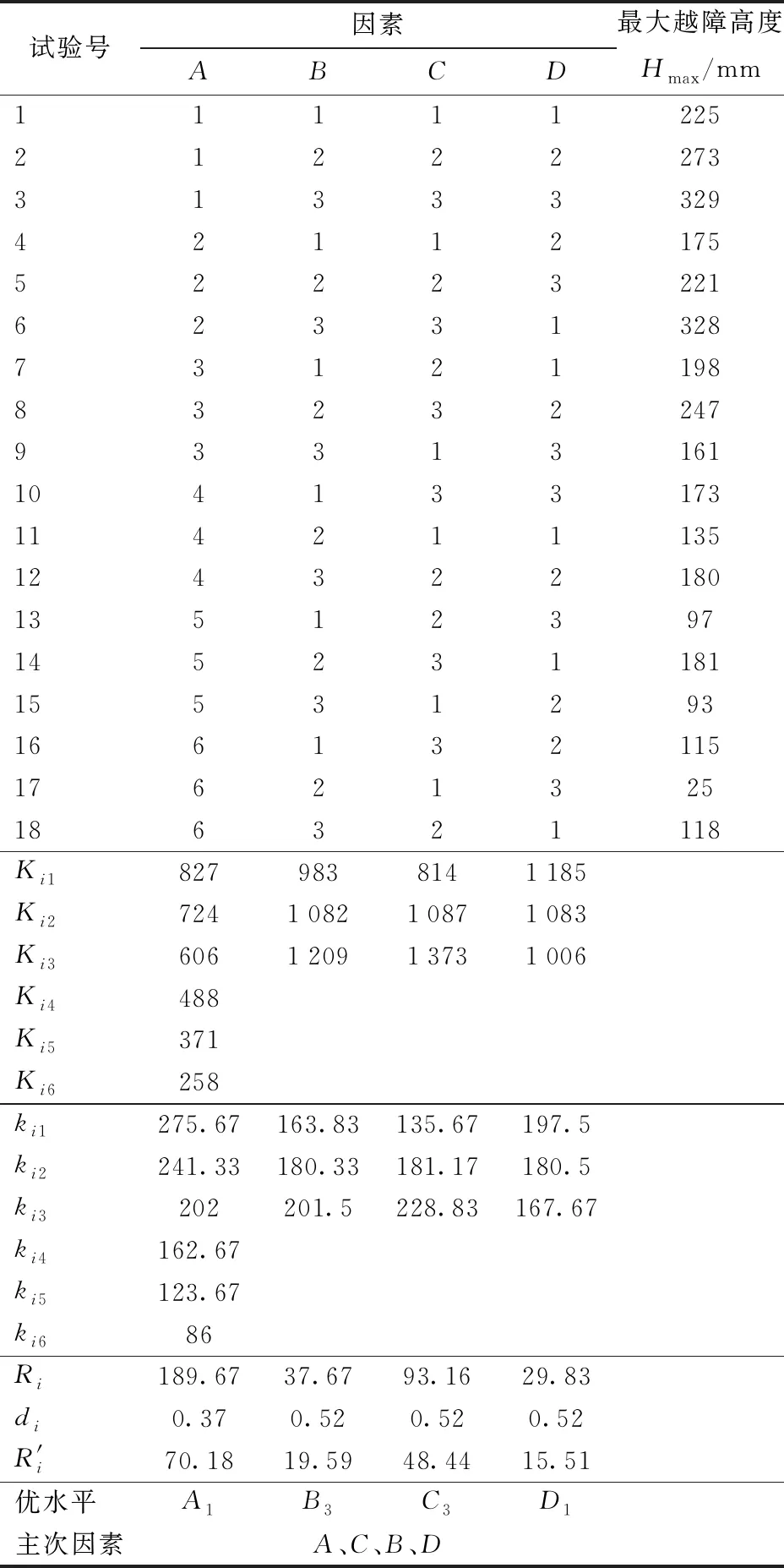
表4 仿真方案及结果Tab.4 Scheme and results of simulation

R′i=diRi

(16)

当因素水平数为6和3时，di分别取0.37和0.52[32]。

为进一步分析各因素对试验指标影响的显著性，在显著水平0.05下对仿真结果进行方差分析，结果如表5所示。

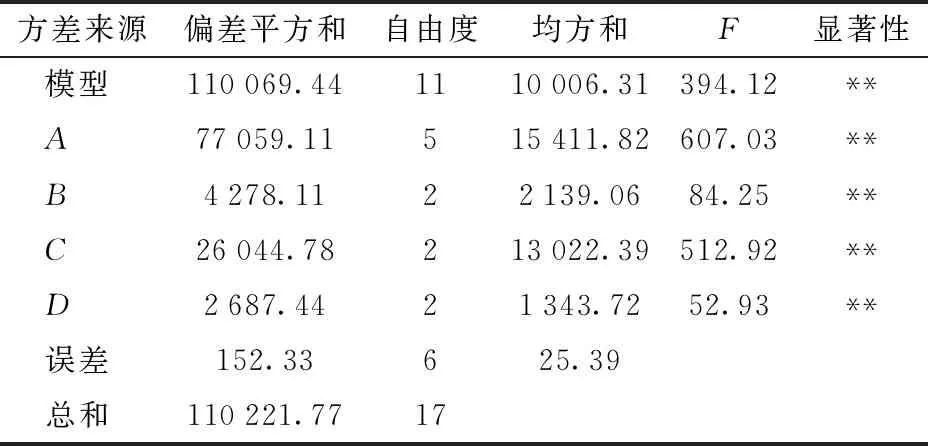
表5 方差分析Tab.5 Variance analysis

由表5可知，α、k、vO及h对于Hmax的影响均非常显著(P<0.05)，且由F值可知，4个因素对于Hmax的影响程度排序为A>C>B>D，即4个因素对Hmax的影响程度由大到小分别为α、k、vO、h。

对仿真结果进行多元回归，可得到山地拖拉机在不同参数下的最大越障高度简易计算公式为

(17)

式(17)可用于任意型号山地拖拉机最大越障高度计算。

2.4 单因素变量仿真试验与分析

为了直观地反映出各因素对于Hmax的影响规律，分别以上述4个因素为变量，其它因素选取优水平进行仿真，并对比理论计算结果，得到各因素对于最大越障高度的影响规律，结果如图7所示。

由理论曲线和仿真曲线可知，Hmax随vO以及k的增大而增大(如图7b、7c所示)，因此提高了山地拖拉机爬坡越障性；相反，α和h的增大则会阻碍山地拖拉机爬坡越障性能的提高(如图7a、7d所示)。另一方面，随着各因素水平值的改变，仿真曲线与理论曲线变化趋势相同，但由于在理论计算时未考虑拖拉机质心偏移，并假设台阶与履带为刚体，因此各因素水平所对应的仿真值与理论值存在偏差，且均小于理论值。针对上述偏差进行分析，结果如表6所示。

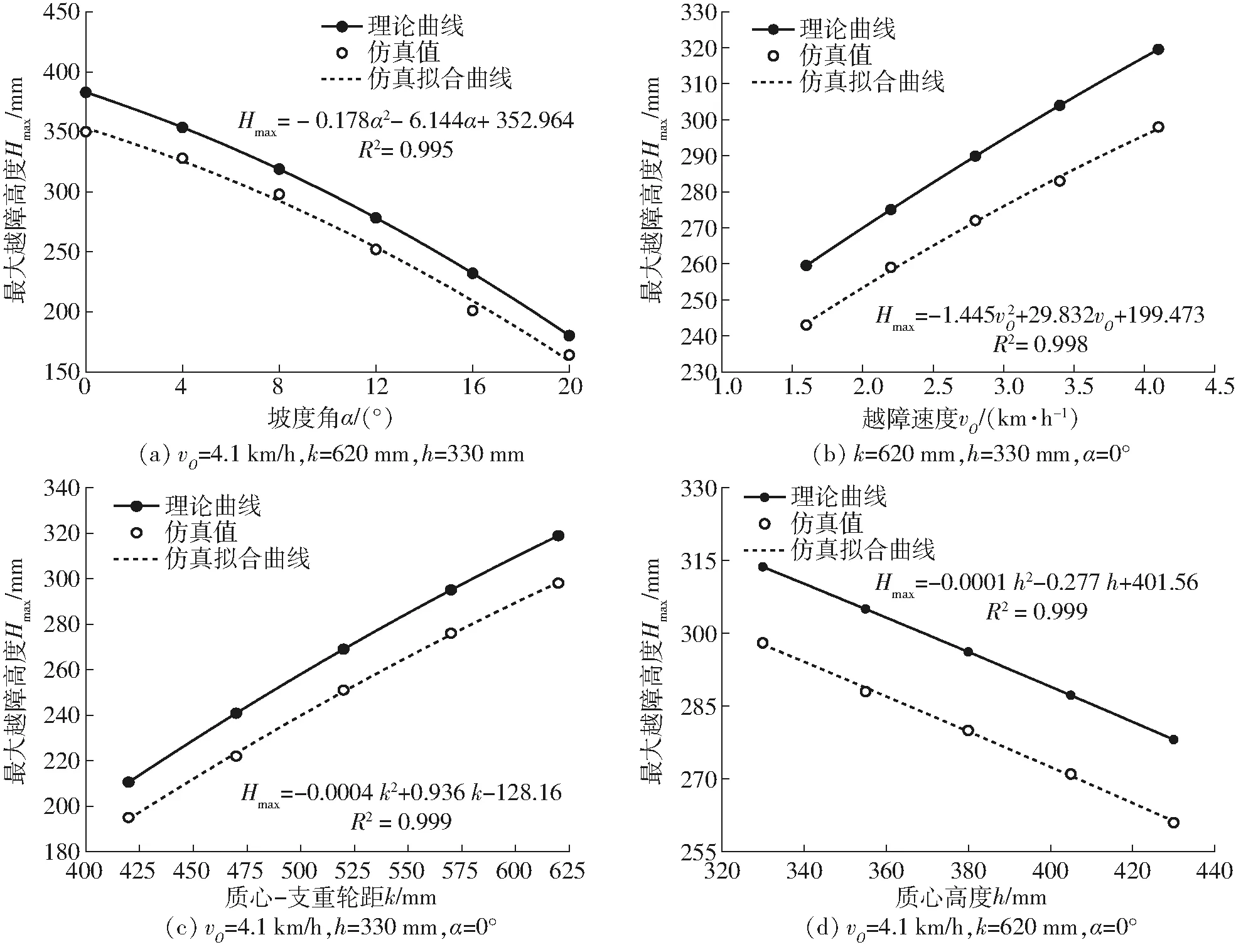
图7 单因素为变量的最大越障高度变化曲线Fig.7 Changing curves of Hmax for variation of single factors

表6 仿真值与理论计算的相对偏差Tab.6 Deviation between simulation values and theoretical calculations

由表6可知，因素A(坡度角)引起的相对偏差最大，且随着坡度角的增加而增大。原因在于仿真环境下山地拖拉机越障时的质心偏移量随仰角增大而不断变化，导致k减小及h增加，从而进一步引起Hmax的减小。

另外，各因素对于仿真值与理论值之间相对偏差的影响由大到小分别为坡度角、质心-支重轮距、越障速度、质心高度，与影响Hmax的顺序相同。因此，对Hmax影响越大的因素，其导致的仿真值与理论值之间的偏差越大。

3 坡地纵向越障田间试验

3.1 试验方案及步骤

依据GB/T 15833—2007、文献[33]，采用本团队研制的山地履带拖拉机物理样机进行最大越障高度的测试，试验地点选在西北农林科技大学北校西区坡地。该坡地土质较硬，纵向坡道长度大于20 m，坡底有5～10 m的平路段，满足试验需要，且坡度角范围较大，便于根据试验要求选择合适的坡道进行试验。

试验首先将横截面尺寸相同(长、宽为1 200、200 mm)、高度不同的台阶(木质立方体)每隔5 m依次沿纵向坡道方向埋入土壤并压实周边，台阶高度由60 mm开始，以20 mm为差值依次递增(原理如图8所示)；将山地履带拖拉机预热到正常工作温度后，用最低挡由坡底的平路起步，油门全开向坡上行驶，由低到高依次跨越各个高度的台阶，直至不能越过为止；记录山地履带拖拉机所能跨越的台阶最大高度，每组试验沿台阶长度方向测量10个数据，试验过程如图9所示。

图8 爬坡越障试验原理图Fig.8 Schematic of obstacle negotiation experiment

图9 田间试验过程Fig.9 Process of field experiment

3.2 试验结果与分析

山地拖拉机在不同坡度角时的最大越障高度如表7所示。由表7可知，当坡度角为0°～15°时，理论计算及仿真试验得到的结果与实测数据的相对误差均小于6.50%(平均相对误差分别为3.65%、5.10%)；当坡度角大于15°时，相对误差明显增大(平均相对误差分别为16.17%、22.79%)，说明所建立的最大越障高度数学模型及仿真模型仅在坡度角较小(0°～15°)时有效。

表7 试验结果与相对误差分析Tab.7 Results and relative error analysis

将仿真值与实测结果对比可得，所有坡度角变化范围内，仿真值均小于实测结果，如图10所示。原因在于，仿真时台阶表层土壤被履带行走系破坏，降低了履带对于土壤的附着能力，从而降低了山地拖拉机的越障能力，而实测时采用木质障碍物，其表层结构不会被履带行走系破坏，履带的附着能力不会受到影响。

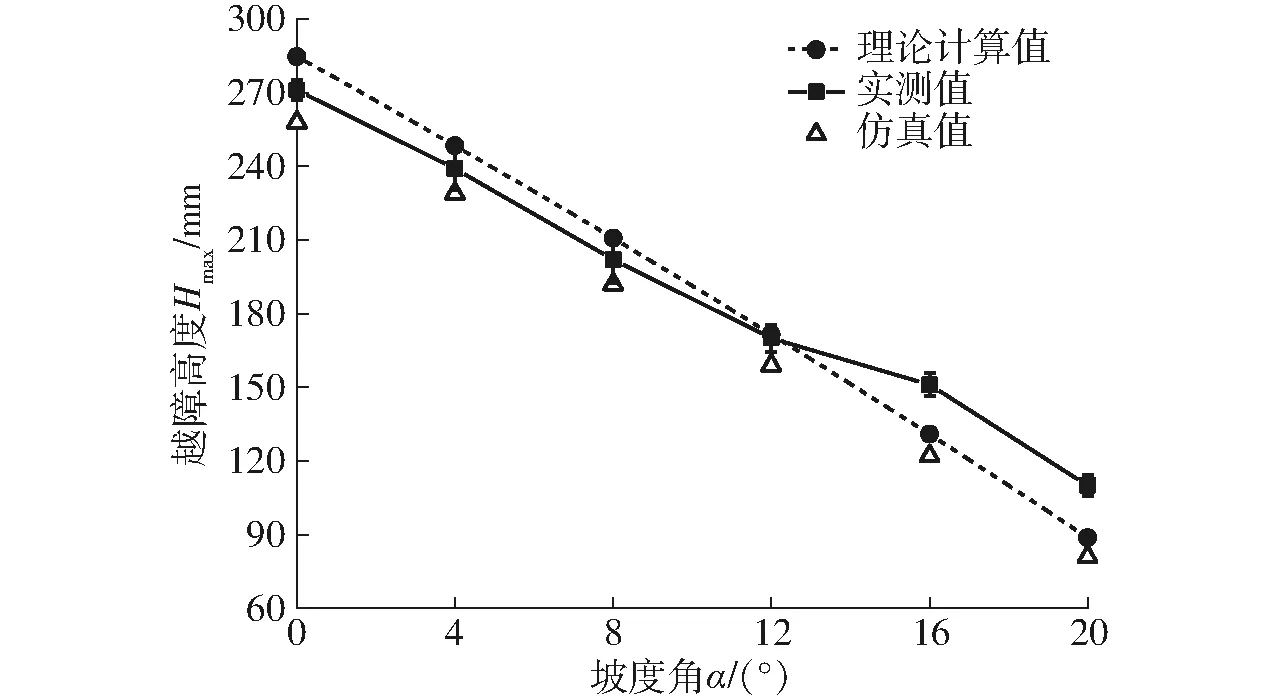
图10 试验结果与理论值、仿真值的对比Fig.10 Comparison between test results with theoretical and simulation values

另一方面，在坡度角较小时，理论值与试验结果较为相近，而坡度较大时，实测结果明显高于理论值，原因在于理论分析山地拖拉机越障第2阶段时假设履带始终张紧，并未考虑履带适应坡道平面与台阶形状而产生变形。在实测试验中，该变形提高了履带的附着能力，以进一步对拖拉机的爬坡越障性能产生积极影响，而且随着坡度角的增大，实测结果与理论值的差值变大，说明在坡地工况下履带的附着能力将对山地拖拉机的越障性能产生重要影响。

4 结论

(1)分析了山地履带拖拉机爬坡时跨越台阶的运动过程，得到求解最大越障高度的计算公式。分析结果表明，坡度角、越障速度及质心位置是影响山地拖拉机爬坡越障性能的主要因素。

(2)设计了基于仿真的正交试验，通过RecurDyn软件仿真得到山地拖拉机在不同工况及质心位置下的爬坡最大越障高度。试验结果的方差分析表明，显著影响山地拖拉机坡地纵向越障性能的各因素主次顺序为：坡度角、质心-支重轮距、越障速度、质心高度。

(3)对爬坡越障性能的影响因素分别进行单因素变量仿真试验，并与理论计算值进行对比，结果表明，增大越障速度和质心-支重轮距、减小坡度角和质心高度可提高拖拉机的爬坡越障性能；对越障性能影响越大的因素，其仿真值与理论值之间的相对偏差越大。

(4)进行了山地拖拉机的坡地纵向越障田间试验，将试验结果与理论计算、仿真结果进行比较。结果表明，在速度为1.6 km/h、坡度角为0°～15°时，试验值与理论计算及仿真结果基本一致，理论计算与仿真试验的最大相对误差分别为5.17%和6.47%；在坡度角大于15°时，理论计算与仿真试验最小相对误差分别为13.25%和19.21%，说明所建立的理论及仿真模型在坡度角较小(0°～15°)时有效。