一种新的双树复小波在Φ-OTDR信号降噪中的应用∗
2020-10-10
(海军工程大学电子工程学院 武汉 430033)
1 引言
随着海底光缆通信技术的发展,海底光缆通信系统规模越来越大,逐渐成为了不可替代的基础性通信设施。由于人类海洋资源开发利用,渔业,军事活动日渐频繁,导致海底光缆阻断事故频发。同时早期建设的海底光缆通信线路运行时间已经逼近了设计寿命。海光缆安全监测技术的实际应用显得尤为迫切。基于后向瑞丽散射效应的光时域反射技术一直是光缆安全监测领域研究的热门,今年来,相位敏感光时域反射技术(Φ-OTDR)以其监测距离远、灵敏度高、响应频率高、单端传感等优势成为海光缆监测技术研究的重点[1]。
光在光纤中传输的损耗,随着传输距离增大,Φ-OTDR系统探测脉冲光在光纤中的后向瑞利散射信号也随着传感距离的增加而变得微弱,以至于湮没在噪声中,限制了监测距离。系统的噪声主要包括光路系统噪声、光电转换噪声、信号采集电路噪声以及环境噪声,通过适当数字滤波方法进行前期的信号降噪处理可以有效地降低环境噪声和电路噪声对Φ-OTDR传感信息的影响,增强信噪比,提高系统性能。
早期使用线性滤波器进行降噪处理,但存在盲区展宽和降噪效果不明显等缺点。2011年蔡李花,方海峰将小波变换应用到了光纤传感系统信号降噪处理[2],滤除了绝大部分噪声。尚静,Qin Zengguang等也分别提出了在Φ-OTDR中使用小波变换降噪的方法[3~4]。
1998年Nick Kingsbury提出了适用于图像处理的双树复小波变换[5]。2012年Chen.G等人提出了基于相邻小波系数去噪的双树复小波变换方法[6]。2017年,Hao H提出多变量经验模态分解小波变换去噪的新方案[7],Naveed K等提出了基于拟合优度的双树复小波去噪方法[8]。近期,针对现有双树复小波变换去噪方法中平移不稳定和信号系数错误估计问题,进一步改进了双树复小波去噪方法,这种方法被命名为DTCWT-GOF-NeighFilt方法。
2 基本原理
2.1 小波变换去噪原理
2.1.1 小波变换基本原理
设ψ(t)为给定的一个函数,则小波变换定义为
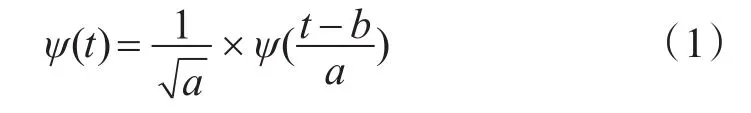
其中,a,b为常数,a>0。对于平方可积的信号x(t)的小波变换定义为
通常简写为 <x(t)⋅ψa,b(t)> 。
这里a,b,t均为连续值,a是尺度因子,作用是对ψ(t)进行伸缩;b是时移因子,作用是确定被分析的x(t)的中心时间。式(2)又称为连续小波变换。ψ(t)为基本小波,ψa,(bt)为小波基函数,是经过基本小波平移和伸缩变换得来。
若采用的小波ψ(t)满足条件,则连续小波存在着逆变换:
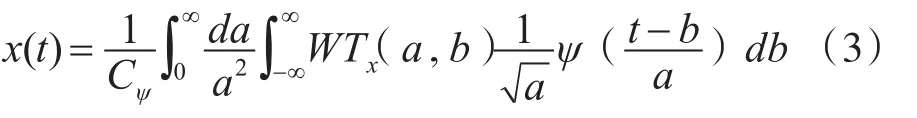
类似的存在离散小波变换对[9]:
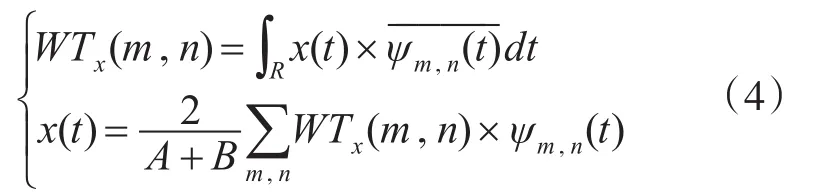
其中离散小波序列{ψm,n(t)}m,n∈Z构成一个框架,其上下界为A,B。
2.1.2 小波去噪基本原理
在实际信号中通常包含噪声,通常先对信号进行降噪处理。信号经过小波变换后,有用信息的小波系数通常较大,噪声的小波系数通常较小,并且有用信息成分决定的小波系数要大于噪声成分决定的小波系数,通过选取合适的阈值保留信号的有用信息成分系数,置零噪声成分系数,然后对信号进行小波重构,达到降噪的目的[10]。
小波去噪通常分为三步,第一步,选取合适的小波基,对信号进行小波分解,通常为三层小波分解。第二步,选取合适的阈值方法,对小波系数进行阈值操作,常见的阈值操作通常分为硬阈值和软阈值操作。
第三步,将阈值操作后的小波系数重构,得到降噪后的信号。

图1 小波阈值去噪过程框图
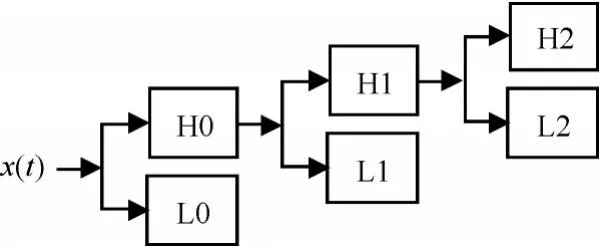
图2 小波三层分解示意图
2.2 双树复小波变换去噪原理
离散小波变换具有良好的降噪效果,但仍存在缺乏平移稳定性、分解过程中存在频率混叠、重构过程中存在伪影等不足。为了克服这些问题,Nick Kingsbury提出了双树复小波变换[5]。双树复小波通过双树结构把信号分解为实系数的实树和虚部系数的虚树[5]。双树复小波的平移稳定性更好,频率混叠更少,实树和虚树分别进行离散小波降噪,从而达到更优的降噪效果。信号的分解和重构流程如图3。

图3 双树复小波信号三层分解及重构示意图
2.3 DTCWT-GOF-NeighFilt去噪原理
传统的小波变换的去噪策略是基于多尺度噪声收缩,即通过判断小波系数和阈值来甄别有用信息和噪声。根据有用信息对应小波系数和噪声对应的小波系数在邻域内具有不同的统计特性和确定性,开发出了基于邻域多尺度去噪策略。Rehman N提出了基于局部拟合良好度(local goodnessof-fit,GOF)和基于经验分布函数(empirical distribution function,EDF)分布特性确定的邻域统计依赖度来进行阈值操的去噪策略[11]。该策略的不足有两点,一是缺乏平移稳定性,去噪后的信号中有伪影;二是有用信息对应的系数被错误当成噪声系数,造成信号细节的丢失。
DTCWT-GOF-NeighFilt去噪策略针对这两个问题做了改进。一是采用双树复小波进行信号分解,使新的去噪策略具有近似平移稳定特性。二是利用一个邻域中大多数噪声系数分类特性来恢复被误判为噪声的有用信息系数。从而提升去噪性能。
该策略具体分为三步。
第一步是基于GOF检测初步分类。
首先计算复小波系数和参考噪声高斯分布之间的相似性τ。Fr(xi)为参考高斯分布函数。

阈值T由式(6)确定

其中Pfa表示有用信息被错误当成噪声的概率。
当τ≤T时,相应系数Η0判定为噪声对应的小波系数,当τ>T时,相应系数Η1判定为有用信息对应的小波系数。
第二步是基于GOF阈值操作。
对于DT-CWT的1到k尺度,分实树和虚树逐层确定参考高斯分布Fℜk(x),Fℑk(x);以及小波系数和参考噪声高斯分布之间的相似性。最终根据给定的Pfa k确定Tk。
由Η0:τk≤Tk和Η1:τk>Tk进行小波系数阈值操作,用表示。
第三步是基于多数分类邻域滤波。
通过后处理恢复错误判定为噪声的有用信息。即检测被判定为噪声系数是否在邻域内被其他噪声系数包围,如果是,则判定为噪声系数并置零。反之如果被有用信息系数包围,则判定为有用信息并保留该系数。最后通过DT-CWT逆变换重构信号sˆ。

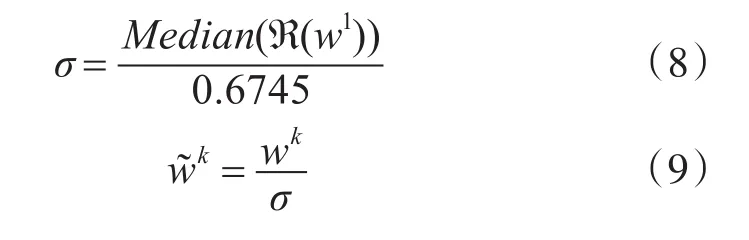
3 仿真
3.1 DTCWT-GOF-NeighFilt数据处理
模拟一组实值已知的Φ-OTDR数据x并做归一化处理,通过Matlab软件编程,使用DTCWT-GOF-NeighFilt方法进行降噪处理,结果如图4所示。
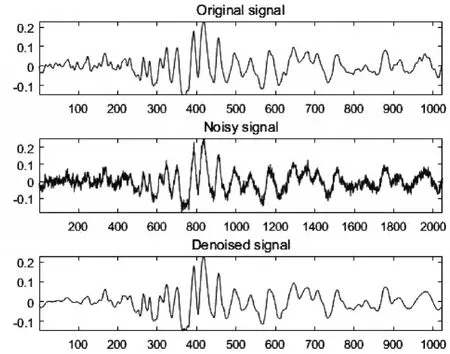
图4 DTCWT-GOF-NeighFilt方法降噪效果对比图
由图4可知DTCWT-GOF-NeighFilt方法降噪效果良好,计算得出,降噪后信号信噪比SNR=18.2142,降噪后信号与原信号的标准差为0.0070。
3.2 与其他小波变换的比较

图5 三种降噪方法效果对比
分别使用硬阈值、软SURE阈值小波变换对3.1中x进行降噪处理,并与3.1中降噪情况对比。结果如图5。
从图5中可以看出,这三种方法都能较好地完成降噪功能,我们计算这三种方法降噪后数据的信噪比并分别和原始数据做差求得标准差,结果如表1。

表1 三种降噪方法效果对比
从表1中可以看出,DTCWT-GOF-NeighFilt方法降噪后的信号信噪比最高,大约比硬阈值降噪增加7dB,比SURE软阈值降噪增加6.5dB。从降噪后数据与原数据做差的标准差也可以看出双树复小波方法的降噪后数据和原数据最接近,降噪效果最好。
4 结语
本文基于对Φ-OTDR散射信号的分析,通过三种降噪方法的对比仿真研究可知,DTCWT-GOFNeighFilt方法对数据中的高斯噪声具有优秀的降噪效果。可用于Φ-OTDR数据预处理的降噪过程,能有效降低Φ-OTDR系统中的高斯白噪声,增强系统信噪比,提高系统性能。
