基于时空相关性的短时交通流预测模型
2020-10-09高小婷


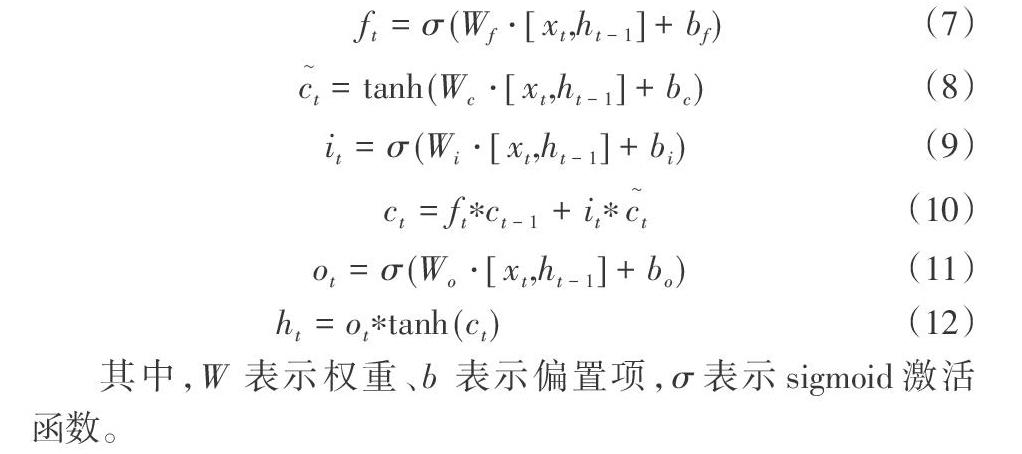
摘要:准确、有效的交通流预测为智能交通系统提供数据基础,是实现道路交通状况预测和交通管控的重要技術之一。本文提出一种基于时空特性的经验模态分解(EMD)和长短期记忆(LSTM)神经网络相结合的交通流预测模型。首先,对交通流序列进行EMD分解得到具有不同时间尺度的本征模态分量,然后,结合空间特性采用LSTM神经网络对交通流进行预测。通过仿真实验可得:与传统的LSTM神经网络相比,基于时空特性的EMD-LSTM预测模型的均方根误差分别减少了3.81;平均绝对误差分别减少了2.29。
关键词:短时交通流预测;经验模态分解;时空特性;长短期记忆单元
中图分类号:TP311 文献标识码:A
文章编号:1009-3044(2020)18-0012-03
开放科学(资源服务)标识码(OSID):
随着人工智能技术的发展,新一代智能交通系统提出了更加自主高效、安全智能的道路交通管理体系,短时交通流的预测就是其重要的研究方向之一[1]。准确、有效的道路短时交通流预测不仅能为新一代智能交通系统提供数据基础,还能够帮助人们规划出行路线,缓解交通压力带来的道路拥堵等问题。目前,国内外学者对于短时交通流预测的研究主要分为四种预测模型,即基于统计分析的预测模型、非线性理论模型、智能预测模型和混合预测模型[2]。
第一类,基于统计分析的预测模型主要包括时间序列法、卡尔曼滤波分析法等。S.Vasantha Kumar和Lelitha Vanajakshi[3]提出一种改进的自回归积分移动平均模型(Auto-Regressive In-tegrated Moving Average,ARIMA)根据不同季节的数据差异进行交通流预测,但是单一的ARIMA方法在处理非线性交通流数据时具有局限性。柳立春等学者[4]提出的卡尔曼滤波模型应用于交通流预测取得了显著效果,但缺点是只适用于实时数据预测。
第二类,非线性理论模型主要依据交通流数据非线性的特点进行预测研究,常用的非线性理论模型有混沌理论模型等。Attoor Sanju Nair等学者啪验证了交通参数的混沌特性,将混沌理论引入了交通流预测的模型中。廖荣华、兰时勇、刘正熙等学者[6]通过改进混沌时间序列局域法,分析预测了北京市的交通数据,最终验证了改进后的方法预测更加准确。
第三类,智能预测模型主要利用机器学习算法对道路交通流量进行预测。Osama Mohammed和Jalil Kianfar[7]通过比较深度神经网络、分布式随机森林、梯度提升机、广义线性模型四种算法对短时交通流的预测效果,得出深度神经网络预测效果更佳。晏臻,于重重,韩璐等[8]提出基于时空特性的CNN-LSTM模型预测交通流,CNN(Convolutional Neural Network.CNN)挖掘数据的空间相关性,LSTM挖掘数据的时序特性,验证了考虑时空特性方法的有效性。
本文提出一种基于时空特性的经验模态分解和长短期记忆神经网络结合的混合模型对交通流进行预测,并验证其预测效果。
1 基本原理
1.1 经验模态分解
经验模态分解( Empuical Mode Decomposition,EMD)[9]是一种自适应的数据挖掘、时频信号处理方法。该方法的主要思想是根据被分解信号自身的时间尺度特性进行信号分解和处理,最终将原始信号分解成若干个本征模函数(Intrinsic ModeFunction,IMF)和一个具有信号平均趋势的残余项。因此,理论上EMD算法适用于任何信号的分解,尤其在分解和处理非线性、非平稳的信号时,比传统的小波分解和傅里叶分解表现出明显的优势。EMD算法的具体实现步骤如下:
(1)找到原始信号序列x(t)所有的局部极大值点和极小值点。根据三次样条插值方法将所有的极大值点拟合成上包络线U(t),所有的极小值点拟合成下包络线/(t),并计算出上、下包络线的平均值,用m,,表示:
m11=1/2[U(f)+L(f)]
(1)
将原始信号与均值包络相减得到第一步分解的新信号,并用h11表示:
h1=x(t)一m1(t)(2)
(2)若h11(t)满足平均包络值为零、并且极值和零值的数量相差0或1,则h11(t)为一级IMF分量。否则,对h11(t)重复进行第(1)步运算,直至第k次分解之后的信号h1k (t)满足成为IMF分量的条件。一级IMF分量可以记作c1(t)
1.2 LSTM神经网络
长短期记忆( Long Shofi-Term Memory,LSTM)结构在原有的输入门和输出门的基础上增加了遗忘门以后,使LSTM能很好地解决“梯度消失”和“梯度爆炸”[10]问题。LSTM不仅对输人数据具有记忆性,而且学习当前网络结构的权重,对于长时间序列的处理具有较大的优势,被广泛应用于自然语言处理、。
如图1所示,是一个LSTM网络的展开结构。由于LSTM结构具有“记忆”,当前t时刻的单元状态ct由t时刻的输入xt和t一1时刻的单元状态ct-1共同决定。ht是t时刻的隐藏层输出。LSTM结构由多个“记忆模块”(memory cell)组成,每个cell包含三个门:输入门、遗忘门和输出门。遗忘门:这部分是决定从cell中遗弃哪部分信息。该门会读取ht-1,和xt,使用sigmoid函数输出一个在0到1之间的数值给每个在cell的上一时刻状态ct-1。其中1表示“完全保留”,0表示“完全舍弃”。输入门:这部分决定输入多少信息加入cell中来。实现这部分需要两步:第一步,“input gate layer”的sigmoid函数决定哪些信息需要更新;用tanh函数生成一个更新的内容c,。第二步,对cell的状态进行更新,将ct-1更新为ct。旧的单元状态与ft相乘,再和i*ct相加,构成新的候选值。候选值随着每个状态的更新程度而变化。输出门:这部分运用一个sigmoid函数来决定cell中被输出的信息。然后,把单元状态通过tanh进行处理,得到一个在一1到1之间的值,再乘以sigmoid的输出,决定最终输出的那部分信息。公式7-12反映了“记忆模块”内部的算法流程。
1.3 基于时空特性的短时交通流预测模型
结合EMD算法对非线性、非平稳时序信號分解处理的优势和LSTM神经网络对长时间序列学习和预测的优势,提出了基于时空相关性的EMD-LSTM模型对交通流数据进行预测。该算法既体现了单个检测点交通流数据在时序上受自身历史数据特性影响的时间相关性,又体现了不同检测点之间交通流数据在空间上受道路上下游地理位置影响的空间相关性。
基于时空特性的EMD-LSTM算法原理如图2所示,该算法先对多个检测器的原始信号分别进行EMD方法分解,将不同检测器的同一级IMF分量组合成新向量,该组合向量同时具有时间尺度和空间特性。将组合向量输入到LSTM神经网络结构进行训练,通过调整参数得出最佳训练网络结构。然后对每一个组合向量进行预测,最终得到某一未来时间段内不同检测器同一级IMF分量的预测结果。再分别将同一检测器的每级IMF分量相加,即可得到所有检测器未来时间段内的交通流预测结果。
2 仿真实验
2.1 数据来源
本文以美国加利福尼亚运输部的性能测量系统( Caltrans-Performance Measurement System,PeMs)数据库的交通流作为数据来源。选取2018年6月1日到2018年6月30日标号为110-E的高速公路上9个连续检测器(编号依次为VDS717367、VDS717369、VDS717373、VDS717376、VDS717379、VDS717381、VDS717383、VDS717387、VDS718130)的交通流量数据作为交通流预测研究的数据集。抽样时间间隔为5min,共约77,760条连续性数。对30天的数据进行仿真实验,取前18天的交通流数据作为训练数据,中间6天的交通流数据作为验证数据,后面6天的数据作为测试数据。
2.2 实验环境
仿真实验使用的软硬件平台如下表所示:
2.3 算法评价指标
为了客观比较不同算法的准确性,本文采用均方根误差( Root Mean Squared Error.RMSE)和平均绝对误差(Mean Abso-lute Error.MAE)两个指标来评价算法预测性能的优劣。两者数值越小说明预测误差越小,算法的准确性越高。
3 结果分析
LSTM神经网络对第5个检测器(编号:VDS717379)的交通流数据进行预测:网络层数为1,隐含层的单元数为100,输出层的单元数为l,三维输入,对交通流的三个参数同时进行预测,初始学习速率为0.001,激活函数为relu、线性函数为linear,优化算法为Adam,迭代次数为200。
经过仿真实验得到LSTM算法误差性能指标值分别为:RMSE=21.568,MAE=15.678。交通流数据预测值与真实值的对比效果图如图3所示,图中预测值曲线与实际值曲线的拟合效果较差,部分预测值比实际值偏大,局部极值点的预测偏差较大。
EMD分解得到8个IMF分量,所以,时空EMD-LSTM模型需要8个单层神经网络;隐含层单元个数分别为[70,100,60,200,50,30,30,70],L2正则化方法的系数大小分别为[0.0001,0.00001,0.0,0.0,0.0,0.0001,0.0001,0.0001],输出层的单元数为1,初始学习速率为0.001,激活函数为relu、线性函数为linear,优化算法为Adam,迭代次数为200。为了提高训练效率,设置了提前停止。经过仿真实验得到基于时空特性的EMD-LSTM模型预测9个检测器数据的误差指标如表2所示:
其中第5个检测器(编号:VDS717379)的误差指标为:RMSE=17.758.MAE=13.388,比LSTM算法分别减小了3.81和2.29。交通流数据预测值与真实值的对比效果图如图4所示。与图3相比,图4中预测曲线与实际曲线的拟合效果明显得到了改善,局部极值点处的拟合效果更好,部分波动剧烈极值点的预测效果更好。
综上所述,基于时空特性的EMD-LSTM模型能同时预测多个检测器的交通流数据,并且预测效果优于传统的LSTM算法。
4 结束语
本文提出的基于时空特性的EMD-LSTM组合模型对短时交通流具有良好的预测效果。与传统的LSTM算法相比,误差性能指标RMSE减少了3.81,MAE减少了2.29;并且该模型能同时预测多个检测器的交通流数据。
参考文献:
[1] Javed M A,Zeadally S,Hamida E B.Data analytics for coopera-tive intelligent transport systems[J].Vehicular Communications.2019.15:63-72.
[2]赵宏.翟冬梅,石朝辉.短时交通流预测模型综述[J].都市快轨交通,2019,32(4):50-54.
[3] Kumar S V,Vanajakshi L.Short-term traffic flow prediction us-ing seasonal ARIMA model with limited input data[J].Europe-an Transport Research Review. 2015,7(3):21.
[4]柳立春.基于卡尔曼滤波的长江武汉大桥段交通流预报[D].大连:大连海事大学,2018.
[5] Nair A S,Liu J C,Rilett L.et aI.Non-linear analysis of trafficflow[C]//ITSC.lEEE Intelligent Transportation Systems.Proceed-ings (Cat. No. OITH8585), Oakland. CA. USA. IEEE. 2001:681-685.
[6]廖荣华,兰时勇,刘正熙.基于混沌时间序列局域法的短时交通流预测[J].计算机技术与发展,2015,25(1):1-5.
[7] Mohammed O.Kianfar J.A machine learning approach to short-term traffic flow prediction:a case study of interstate 64 in Mis-souri[C]//2018 IEEE International Smart Cities Conference(lSC2),September 16-19. 2018. Kansas City, MO, USA. lEEE,2018: 1-25。
[8]晏臻,于重重,韩璐,等.基于CNN+LSTM的短时交通流量预测方法[J].计算机工程与设计,2019,40(9):2620-2624,2659.
[9]关莹莹.基于深度学习的ITS短时交通流量预测算法研究[D].哈尔滨:哈尔滨工业大学,2019.
[10]杨祎玥,伏潜,万定生.基于深度循环神经网络的时间序列预测模型[J].计算机技术与发展,2017,27(3):35-38,43.
【通联编辑:光文玲】
基金项目:河北省高等学校科学技术研究重点项目( No.ZD2019010)
作者简介:高小婷(1992-),女,硕士研究生,主要研究方向为智能信息处理。
