基于光锥求和规则和重夸克展开跃迁形状因子的计算
2020-10-09左亚兵郝燕南张卫荣
左亚兵, 陈 岩, 凌 汶, 杨 威, 郝燕南, 张卫荣
(辽宁师范大学 物理与电子技术学院,辽宁 大连 116029)
根据夸克模型,介子中包含一对正反夸克.依据轨道角量子数的不同,介子可以分为S波介子(l=0)、P波介子(l=1)、D波介子(l=2)等[1].S波介子包括赝标量介子和矢量介子,是人们研究的最多,也是了解的最充分的一类介子.P波和D波介子可以看作是S波介子的轨道角动量激发态.在早期对撞机实验中,由于这些介子产生的事例数很少且受到探测器精度的限制,人们对这类介子的研究比较少.近十多年来,随着对撞机亮度和探测器精度的提高,实验上给出了许多有关高轨道角动量激发态介子(特别是P波介子)的测量结果,使这一领域引起了人们广泛的关注.


1 B(s)到2++张量介子形状因子的定义与基于重夸克展开的光锥求和规则推导
1.1 B(s)到2++张量介子形状因子的定义

(1)
(2)
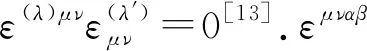
对于味改变中性流(FCNC)诱导的稀有衰变B(s)→Tl+l-,除了上述矢量和轴矢量算符强子矩阵元外,还涉及张量算符强子矩阵元.这些强子矩阵元也可以通过形状因子参数化如下[10],
(3)
(4)
T1、T2、T3称为企鹅类型跃迁形状因子.
利用HQEFT对上述强子矩阵元做重夸克展开,只考虑领头阶的贡献[12],有
(5)
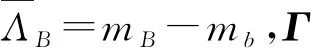
(6)
这里,

(7)
(8)
(9)
(10)
与此类似,取Γ=σμν、σμνγ5,将相应强子矩阵元的领头阶波函数用L′i(i=1,2,3,4)表示,把式(5)、式(6)代入式(3)、式(4),得到企鹅类型跃迁形状因子的表达式如下:
(11)
(12)
(13)
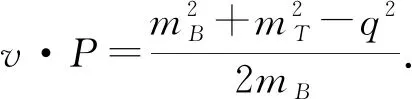
1.2 基于重夸克展开的光锥求和规则推导
利用HQEFT和光锥求和规则计算跃迁矩阵元领头阶波函数L1、L′1、L2、L3、L′3、L4、L′4.参照末态为矢量介子的情形[14],首先,定义真空-张量介子关联函数如下:
(14)
(15)
(16)
(17)

(18)
只考虑重夸克展开领头阶的贡献,把式(5)、式(6)代入式(18),得到

(19)
其中,kμ=(P+q)μ-mbvμ,表示初态重介子的残余动量.积分项对应高共振态的贡献,减除项的引入是为了保证积分收敛,可以通过Borel变换消除,不影响物理结果.F是重介子领头阶衰变常数[12],定义如下:
(20)
也可以从理论角度对关联函数进行计算,
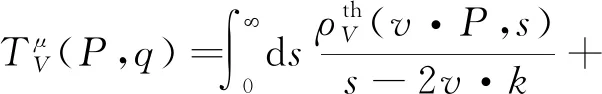
(21)

(22)
令y=v·P、ω=2v·k,对式(21)做连续两次Borel变换,有
(23)
(24)
(25)
从式(15)出发,利用同样的方法可以得到
(26)
(27)
(28)
φ‖(u)、φ⊥(u)、gv(u)、ga(u)、ht(u)、hs(u)、g3(u)、h3(u)为张量介子光锥分布振幅,定义如下[9]:
(29)
(30)
(31)
(32)
其中,φ‖(u)、φ⊥(u)扭度为2,gv(u)、ga(u)、ht(u)、hs(u)扭度为3,g3(u)、h3(u)扭度为4.
从式(16)、式(17)出发,利用上述方法计算与企鹅类型形状因子对应的跃迁矩阵元领头阶波函数L′1、L′3、L′4.结果显示,在只考虑重夸克展开领头阶贡献的情况下,L′1=L1、L′3=L3、L′4=L4.根据式(7)~式(13),企鹅类型跃迁形状因子与半轻类型形状因子存在如下关系:
(33)
(34)
(35)
因此,利用HQEFT,在只考虑重夸克展开领头阶贡献的情况下,只有A1、A2、A0、V四个独立的跃迁形状因子.
2 形状因子的数值结果与讨论

φ‖(u)=φ⊥(u)=30u(1-u)(2u-1),
(36)
gv(u)=5(2u-1)2,
(37)
ga(u)=10u(1-u)(2u-1),
(38)
(39)
hs(u)=15u(1-u)(2u-1).
(40)

表1 基于QCD求和规则给出的张量介子衰变常数[9]


图1 s0取不同值时,最大反冲点处B→a2(1320)跃迁形状因子随T的变化

(41)


表跃迁形状因子在q2为0时的数值结果与相应a、b的取值

图2 B→a2(1320)跃迁形状因子对q2依赖关系

(42)
(43)
其中,
(44)
(45)
(46)
(47)
L、±分别表示纵向和横向极化的贡献.
对q2积分,得到总的衰变率
Γ=ΓL+Γ++Γ-.
(48)

(49)
取[1]GF=1.166 378×10-5GeV-2,ћ=6.582 119×10-25GeV·s,
|Vub|=(4.09±0.39)×10-3,τB-=1.638×10-12s,
mτ=1.777 GeV,

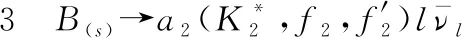
表衰变的分支比和纵向极化分数
4 结 论