Research on full-period acquisition method for diesel enginebased on self-adaptive correlation analysis①

Zhao Haipeng (赵海朋), Mao Zhiwei, Zhang Jinjie② , Lai Yuehua, Wang Zijia, Jiang Zhinong

(*Key Laboratory of Engine Health Monitoring-Control and Networking of Ministry of Education, Beijing University of Chemical Technology, Beijing 100029， P.R.China) (* *Beijing Key Laboratory of High-End Mechanical Equipment Health Monitoring and Self-Recovery, Beijing University of Chemical Technology, Beijing 100029, P.R.China)

Abstract

Key words: diesel engine, key phase, full-period acquisition, vibration signal

0 Introduction

As the core equipment of modern industrial equipment group, diesel engine is widely used in the fields of electric power, transport machinery and military weapons such as vehicles ships and submarines[1]. Compared with other monitoring methods, vibration-based signal collected from sensors contains more useful information of health condition and are easier to be obtained. However, diesel engine is essentially a very complex machine integrating rotating and reciprocating motions. Alternating firing of each cylinder of diesel engine results in the unstable rotation speed and the coupling of vibration excitation, of which vibration signal period is random. Fortunately, corresponding specific relationship exists between working process of each cylinder and crankshaft rotation angle. That is, the specific crankshaft rotation position gives a space physical significance of vibration signal impact characteristic in angle domain. Therefore, it is of great significance to study the acquisition technology of full-period vibration signal used for diagnosis and evaluation of the running state of diesel engines[2].

At present, the acquisition method of full-period signal generally can be divided into trigger sampling of hardware analog and software resampling. The trigger sampling of hardware analog mainly relies on some expensive equipment to generate the key phase signal such as photoelectric pulse encoder or the key phase pulse, phase-locked loop and sampling frequency synthesizer. Software resampling is carried out in this way that the key phase and vibration signals are firstly synchronously sampled at equal time interval and then the interpolation algorithm is applied in the data-process to obtain full-period signal[3,4]. A full-period resampling technology in angular domain is introduced in Ref.[5] for aero-engine. It combines the equal-phase with linear-difference methods taking the high tool signal of rotating speed as the reference. Xu et al.[6]proposed a multi-channel synchronous acquisition method of full-period signal through phase compensation, which is based on the trigger acquisition and resampling technology of key phase signal and then calculates full-period acquisition time with sampling frequency. To solve the problem of low accuracy of helicopters vibration monitoring equipment, Long et al.[7]proposed asynchronous average short-time Fourier transform method to achieve the adaptive whole-period sampling in time-domain. By embedding the linear interpolation prediction module in the FPGA chip, a full-period sampling method with high precision was realized in Ref.[8] based on the key phase frequency multiplication as A/D conversion trigger signal. Combet et al.[9]proposed a full-period sampling method based on time-domain synchronous average, which firstly automatically selected and estimated meshing frequency by using instantaneous rotation speed and key phase signal. Nevertheless, these methods are just suitable for a small number of particular equipment due to requirement of the reference signal generated by key phase impulse device, which are always subjected to mechanical structure and A/D conversion channel. It not only brings inconvenience to the field construction, but also often brings the problem of start-stop running phase, which seriously affects the signal quality and fault diagnosis performance. Besides, it is even more remarkable that this requires more professional technology and brings some safe risks to cause results in poor reliability of industrial equipment.

In order to address the problems above, several advancements in this paper are made in the following aspects. Firstly, a time-frequency method with strong energy concentration is constructed called the synchrosqueezing generalized S-Transform (SGST), which is employed to estimate the meshing frequency based on the vibration signal collected from gear box. Secondly, an adaptive Teager energy operator threshold is introduced to identify the transient impact characteristics related to full-period vibration signal in the cylinder head. Thirdly, self-adaptive correlation analysis (SACA) is designed to achieve the full-period acquisition of vibration signal without key phase, which can realize satisfactory data acquisition accuracy and eliminate phase shifting phenomenon.

1 Feasibility analysis of the proposed method

Vibration signal in cylinder head contains a lot of movement information of key components of diesel engine, which is usually used in fault diagnosis. In recent years, scholars have performed a lot of cutting-edge researches on fault diagnosis. Wang et al.[10]proposed an intelligent fault diagnosis method for diesel engine based on improved adaptive dictionary matching tracing and non-negative matrix decomposition. In Ref.[11], high-order cumulant features of vibration signal image were used to overcome the difficulty in identifying fault features of different parts of diesel engine. Zhang et al.[12]proposed a fault diagnosis method based on the deep convolutional neural network which introduces random discarding and batch standardization criteria to solve the problem of time consuming and low accuracy of traditional diagnosis method for diesel engine firing fault.Based on the fusion method of fast Fourier transform, discrete Fourier transform and neural network, Alireza et al.[13]proposed a state monitoring and combustion fault monitoring method suitable for the 12-cylinder 588 kW diesel engine, which can diagnose and locate the sensor and combustion injection fault. Though many work mentioned above that focus on the energy change of vibration signal have achieved very good results, it fails to address the timeliness and circularity of vibration signal.

The cylinder head vibration signal of four-stroke diesel engine mainly has 4 processes: intake, compression, combustion and exhaust, among which ignition impact, exhaust valve closing impact and intake valve closing impact are most significant, as shown in Fig.1. It can be observed that a complete full-period working process corresponds to the crankshaft rotation angle 720 °, of which each stroke has a certain sequence and a corresponding specific relationship with the crankshaft rotation angle.The results show that it is feasible to propose a new trigger signal by using the timeliness and circularity of vibration signals.

Fig.1 Full-period impact characteristics of cylinder head vibration signal

2 Test-bed of diesel engine

There are strict requirements for the installation and precision of key phase sensor and the process of full-period acquisition is very complex and dangerous in diesel engine such as TBD234V12.In this section, diesel engine is used to verify the effectiveness of the proposed method.The physical diagram of the test-bed device is shown in Fig.2. It is observed in Fig.2 that TBD234V12, as a research object, is a V-type, four-stroke, direct injection diesel engine and the consecution power/speed is 373 kW/1 500 r/min, mainly applied as the power or power generating equipment of ship.

Fig.2 Test-bed of full-period acquisition without key phase:TBD234V12 and sensors

3 The principle of the proposed method

In this section, the principle of the proposed method is introduced including the adaptive Teager energy operator threshold (ATEOT), the synchrosqueezing generalized S-Transform (SGST) and self-adaptive correlation analysis (SACA). In addition,simulations are carried out to validate the high energy concentration in time-frequency distribution of SGST.

3.1 Adaptive Teager energy operator threshold

In fact, there exists strong interference of each cylinder vibration due to the compact-complex structure and the uncertain coupling of vibration transmission path of diesel engine. Therefore, it is not conducive to identify the impact characteristics of the full-period signal. Teager energy operator (TEO), a nonlinear combination operator designed by Kaiser based on signal amplitude and differential value, is now the most common method to identify transient impact. TEO is widely used in the fields of speech recognition and mechanical fault diagnosis because of simple and effective traits[14,15]. In view of the transient impact characteristics of cylinder head vibration signal of diesel engine, in this paper, TEO operator is firstly used to enhance the transient impacts, then the adaptive threshold is applied to identify the first transient impact determined the starting position of intercepting data. For any signalx(i), TEO operator can be defined as

ψ[x(i)]=[x′(i)]2-x(i)x″(i)

(1)

wherex′(i) andx″(i) represent respectively first-order and second-order differential.

Due to the non-stationary signals obtained in practical applications, it is difficult for the traditional fixed threshold method to meet the requirements of identifying transient impacts. Therefore, the adaptive threshold based on the energy level of signal is defined to detect transient impacts and the steps are as follows:

• To define the initial transient impact thresholdtsand initial noise thresholdnslevel. The formulas are listed in Eqs(2) and (3), whereNis the signal length,λandβare the adjustment level factor of the transient impact and noise respectively.

(2)

(3)

• To divide the signal into frames and updatetsandns.

(4)

(5)

(6)

wherealarm(i) is the transient impact andDis the length of framed signal.

3.2 Synchrosqueezing generalized S-Transform

This section begins to study the principle of SGST. As an improved variant of S-Transform, generalized S-Transformation (GST) not only retains the multi-resolution of S-Transform but also enhances adaptability by introducing standard deviation adjustment factor[16,17]. The generalized S-Transformation of signalxis defined as Eq.(7) in finite energy spaceL2(R).

GSTx(t,f)=〈x(t),g(t-τ,σ(f))exp(i2πft)〉

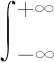
(7)

whereGSTx(t,f) is the S-Transform result andg(t) is the Gaussian window function. The standard deviationσis equal to 1/|f|m, of whichmis the adjustment factor of standard deviation and the value range is (01].

(8)

(9)

(10)

where ∂tGSTx(t,f) represents the partial derivative ofGSTwith respect to time.

From the above equations, it is known that the SGST algorithm proposed in this work has strong energy concentration. In order to verify that it is feasible for SGST algorithm to estimate the transient frequency, the comparisons of time-frequency distribution between the SGST and GST are focused on. Here in, a numerical signalx(t) consisting of multiple transient impacts with different frequency components is modeled as

x(t)=

(11)

s(t)=e-ζtsin(2πft)

(12)

whereI,AiandTrespectively represent the number of transient impacts, the amplitude of theith transient impacts and the delay time interval，ζis a decay parameter. For this numerical signal, the white noise of Guass is added to it, where the signal-to-noise ratio (SNR) is equivalent to 15 dB.s(t) has the transient impact with unilateral attenuation characteristic.

In this paper,Aiandβis respectively set to 1 and -50,Tis set to 0.15 s andIis set to 3. In addition, the frequency of signal components corresponding to 3 transient impacts are 600, 400 and 200 respectively. The sampling frequency is set to 2 000 Hz. The simulation signal waveform in time domain and the fast Fourier transform (FFT) spectrum are shown in Fig.3. For comparison, the time-frequency distribution generated by GST and SGST are shown in Fig.4. It can be seen from Fig.4 that GST and SGST can identify the transient frequency of the impacts.

Fig.3 Original waveform and FFT of simulation signal

Fig.4 The comparison result of GST and SGST

3.3 Self-adaptive correlation analysis

Carl Pearson designed a statistical index-correlation coefficientr, which can reflect the similarity degree between two variables and varies from 0 to 1. There is no correlation betweenxandy, when the absolute value is less than or equal to 0.3; There is a low correlation betweenxandywhen the absolute value is larger than 0.3 and less than or equal to 0.5.It means that there is a significant correlation betweenxandysuch that 0.5<|r|≤0.8. If |r|>0.8, there is a high correlation betweenxandy[20]. Due to the non-stationary signals obtained in practical applications, it is difficult for the traditional fixed threshold method to meet the requirements of full-period signal acquisition. Therefore, the self-adaptive correlation analysis is proposed based on the sliding combination window model, which is composed of series of windows with variable length. To select signal sequence by constantly updating the window and sliding to the right with certain step, the optimum sliding window is obtained by calculating correlation analysis. Model schematic diagram of sliding combination window with variable length is shown in Fig.5. The advantage of the sliding combination window with variable length is that there is no need to design fixed length in advance, which varies continuously according to the length of full-period signal. The design formulas of window length are shown as

wi=[Ti-δi:dj:Ti+δi]

(13)

δi=alogTi

(14)

dj=b(j-1)logTi

(15)

(16)

(17)

wherewiin Eq.(13) is the sliding window,Tiis the estimation period,δiis the window length range,djis the window scale (j=1,…,n),aandbare the adjustable parameters of window length range and window scale (default:a= 100andb=10).rimrepresents the correlation coefficient between themth and (m-1)th signal sequences of theith window.

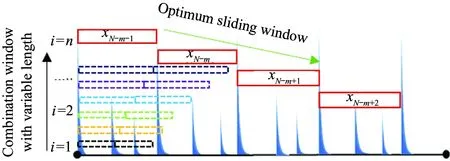
Fig.5 Model schematic diagram of sliding combination

4 Overall framework of full-period signal acquisition without key phase

As described in the above sections, the overall framework of proposed full-period signal acquisition without key phase is shown in Fig.6. In order to weaken other impact disturbances independent of the full-period signal acquisition, an adaptive Teager energy operator threshold is firstly introduced to enhance the transient impact characteristics of vibration signal in the cylinder head, which can be in favor of identifying the impact starting point. And noise reduction of vibration signal collected from gearbox is implemented by applying FIR bandpass filter. Then, the synchrosqueezing generalized S-Transform (SGST) with strong energy concentration, a time-frequency method is constructed, which is employed to estimate the rotation speed of crankshaft and the length of full-period signal. According to the impact starting point and estimated full-period length, initial sequence including multiple full-period signal is obtained. Finally, self-adaptive correlation analysis (SACA) is designed to achieve the full-period acquisition of vibration signal without key phase.

Fig.6 Overall framework of full-period signal acquisition without key phase

5 Experimental result analysis

5.1 Verification of impact identification based on the ATEOT

In this set of experiments, the adaptive threshold performance based on the Teager energy operator is compared with the original vibration signal in cylinder head, of which the comparison results of impact identification are shown in Fig.7. It can be observed from Fig.7(a) that the results of adaptive threshold based on the original signal perform poorly in the impact identification, which includes a lot of disturbances in addition to theoretical impact features in Section 1. In contrast, the impact identification of the proposed ATEOT method is more consistent with the theoretical analysis results, which is beneficial to intercept the full-period signal.

5.2 Verification of time-frequency distribution based on the SGST

From the simulation results mentioned in the Section 3.2, it is known that the SGST algorithm has stronger energy concentration than GST. In this section, the comparison results of time-frequency distribution between GST and SGST are described based on the real vibration signals of TBD234V12 diesel engine gearbox under 3 common working conditions. The time-frequency distribution generated by GST and SGST and verification results of rotation speed are depicted in Fig.8, of which the local time-frequency features are displayed at the right side. It can be observed from Fig.6 that the GST roughly characterizes the time-frequency features of gearbox vibration signal and it fails to extract the ridge information of the meshing frequency. However, the SGST method provides much more aggregated time-frequency features compared to the GST.

(a) Original signal

(b)Teager energy signal

5.3 Overall performance of the proposed method compared with key phase

In practical applications, the vibration signals of mechanical systems are very complex due to the poor working conditions, which may results in the performance degradation of the proposed method. In this section, a series of verifications based on the ATEOT and SGST will be carried out. The overall performance of the proposed method is compared with the traditional method with key phase based on the evaluation factors of periodicity integrity and relative error of the initial phase position. The periodicity integritywand relative error of the initial phase positionELcan be calculated by the following Eqs (18) and (19), whereNkeyandNnon-keyrepresent the number of vibration signal with key phase and without key phase,LkeyandLnon-keyrepresent the initial phase positions of the transient impact with key phase and without key phase.

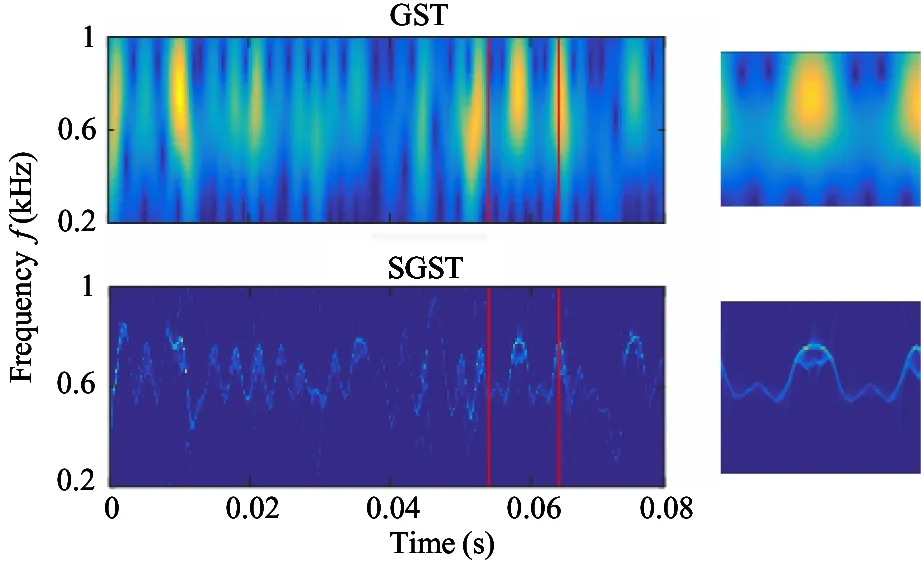
(a) 1 500 r/min

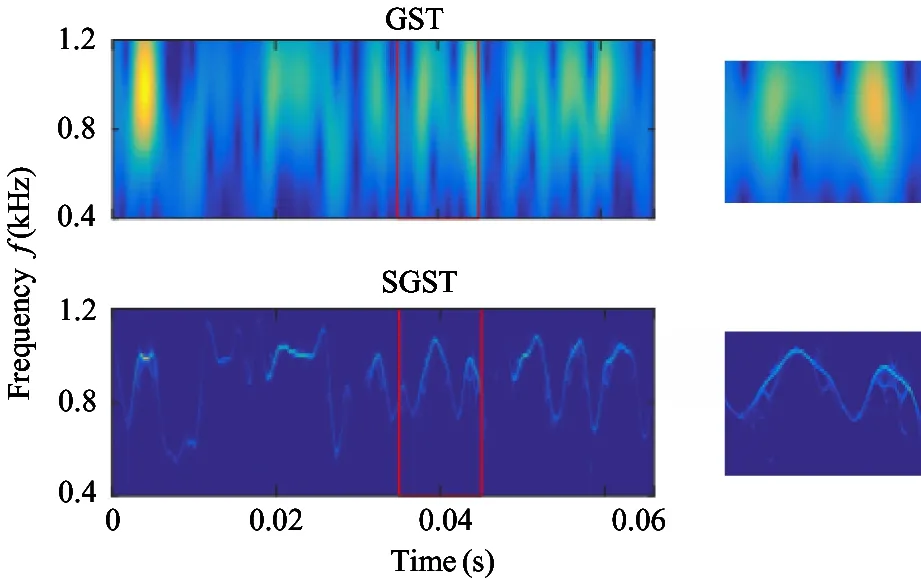
(b) 1 800 r/min

(c) 2 100 r/min

(18)

(19)

According to Eqs(18) and (19), no matter how many iterations, the results of the proposed method is always biased for the results with key phase. The comparison results of periodicity integrity and relative error of the initial phase position are plotted in Fig.9. It can be seen from Fig.9(a) that the periodicity integrity of the proposed method always has wonderful performance under different working conditions. The mean periodicity integrity is as high as 98%. In addition, the periodicity integrity of low-speed condition is better than all other high-speed condition. Fig.9(b) presents the relative error of the initial phase position, of which the relative error is less than 6%.

(a) Periodicity integrity

(b) Relative error of the initial phase position

6 Conclusion

This study proposes a novel full-period signal acquisition method without key phase, to solve the installation problem of special key phase device based on the vibration signals in the cylinder head and gearbox of diesel engine. The main contributions of this study is to construct the time-frequency method with strong energy concentration. An adaptive Teager energy operator threshold is introduced to identify the transient impact characteristics related to full-period vibration signal in the cylinder head. The overall performance of the proposed method are also demonstrated through numerical and experimental verification. The results show that the proposed method can be used to effectively and accurately collect the vibration signals without key phase under different working conditions for diesel engine.