基于FWD动态弯沉盆的旧混凝土板共振碎石化基层沥青加铺结构模量反算

2020-10-09李盛许路凯马永波程小亮

中南大学学报（自然科学版） 2020年8期

李盛，许路凯，马永波，程小亮

(1.长沙理工大学道路灾变防治及交通安全教育部工程研究中心，湖南长沙，410114；2.中冶南方城市建设工程技术有限公司，湖北武汉，430063)

我国早期修建的水泥混凝土高速公路因交通量增长过快及交通荷载和环境的长期作用大多进入了大修阶段。共振碎石化因其能减少大修成本和节约资源保护环境，且水泥混凝土共振碎石化作为基层的沥青路面加铺结构满足设计和承载力要求，其应用越来越广泛，如何快速、精确、无损地评价大修工程的施工质量成为诸多学者研究的重点。目前，人们对高速公路大修工程旧混凝土板共振碎石化基层沥青加铺结构施工质量等方面的检测依旧采用钻芯取样的方法，钻芯取样具有破坏性强、效率低、成本高和代表性差等缺点，而落锤式弯沉仪(FWD)因具有无破损、测速快、精度高等优点，且能较好地模拟行车动态荷载下真实路面结构力学响应，检测结果为弯沉盆弯沉值，同时可自动对路面弯沉值的温度进行修正，因而其应用越来越广泛[1]。在研究过程中，臧国帅等[2]以落锤式弯沉仪(FWD)为平台，以基层模量比为评价指标，对基层反演模量与开裂状况的相关性进行了分析，建立了基层开裂状况无损评价模型和评价标准。DONG 等[3]提出了一种估算沥青层20 ℃标准弹性模量和温度系数的方法，并采用高斯-牛顿法编制了相应的有限元反算程序，确定了路面各层模量和温度相关系数。HAMIM 等[4]建立了有限元模型，通过静态、动态分析，发现瞬态动力分析方法是模拟FWD测试的最佳方法。康海贵等[5]利用落锤式弯沉仪(FWD)所测得的弯沉值，采用系统识别方法进行结构层模量反算，进而分析了沥青路面弯沉值及反算模量与沥青温度之间的关系，并建立了相应的温度修正公式。TAREFDER 等[6]对3 种不同类型的模量反算程序(BAKFAA，MODULUS 和EVERCALC)进行了一致性和精度评价，得出EVERCALC 程序比MODULUS 和BAKFAA 程序具有更好的一致性和准确性。邱欣等[7]采用动力有限元数值分析方法，利用FWD 路表动态弯沉盆系统分析了层间非连续接触行为对半刚性基层沥青路面模量弯沉值反演结果的影响规律。VARMA 等[8]提出基于遗传算法的反算算法(BACKLAVAN)，经过验算发现该算法可以从FWD 试验中推断出AC 层的线性黏弹性和无黏结层的非线性弹性特性。查旭东[9-10]提出基于同伦方法的路面模量反算研究，并在此基础上建立了相应的温度修正公式。蔡聪[11]采用有限元软件建立三维有限元模型分析路面的动力响应，同时利用3 层BP 神经网络对路面模量及面层的横观各向同性系数进行了反算。综上可知，人们基于FWD 的沥青路面研究虽取得一定的成果，但仍有局限，体现在：旧混凝土板共振碎石化基层沥青加铺路面结构较复杂，压密过程不断进行，影响应力和应变的因素更多，规范中没有模量及厚度参考值，针对高路公路大修工程路面施工质量评价的研究很少，现有研究主要是采取钻芯取样、贝克曼梁等方法，无法真实反映旧混凝土板共振碎石化基层沥青加铺路面各结构层在动态荷载作用下的工作性能。基于FWD 动态弯沉盆，通过力学和数学方法进行模量反算，从而评价旧混凝土板共振碎石化基层沥青加铺路面施工质量具有重要意义。为此，本文作者对湖南省高速公路大修工程加铺结构进行研究，利用SIDMOD 和EVERCALC 程序对旧混凝土板共振碎石化基层沥青加铺结构的各结构层进行模量反算，对加铺结构和原路面的结构模量进行评价，并利用有限元软件进行反演模拟分析，以期为碎石化道路施工及设计提供参考和依据。

1 弯沉值采集及结构层划分

1.1 落锤式弯沉仪及其检测原理

FWD 落锤式弯沉仪是目前国际上最先进的弯沉无损检测设备之一，具有操作安全、检测速度快、检测结果准确、适应多变交通环境的特点。FWD 落锤式弯沉仪一般由车载装置、荷载加载系统(包括落锤、承载板)、弯沉检测装置及控制和信息处理系统组成。FWD 落锤式弯沉仪工作时荷载加载装置提起重物并使其自由落体，通过锤击1块具有一定刚性的承载板作用到路面结构，使被测路面产生瞬间变形，并通过按一定间距分布的与路面紧贴的传感器测定道路结构层表面的变形响应，从而得到动态弯沉盆。其工作原理如图1所示，其中，hi为第i层厚度，Ei为第i层的模量。

1.2 弯沉值采集

1.2.1 荷载加载系统

加载时，通过液压装置将重锤提升至一定高度并自由下落，由此产生以脉冲荷载作用于承载板，由承载板传递至路面，荷载可以通过改变提升高度和锤重进行调整。为了简化计算，通常将FWD 所施加的荷载时程曲线简化为荷载峰值(0.714 MPa)，荷载作用半径为15 cm，作用时间为30 ms 的半周期正弦函数圆形均布荷载，如表1所示。

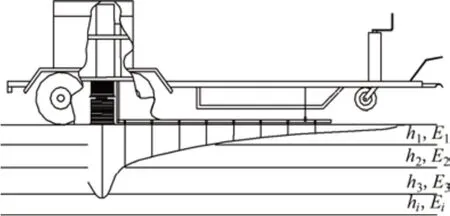
图1 落锤式弯沉仪工作原理图Fig.1 Working principle of falling weight deflectometer

1.2.2 弯沉检测装置

检测采用FWD Dynatest8000 设备，该设备共设置9个传感器。布置传感器时，为提高模量反算时的准确率，以加载点为中心，传感器布置向外逐渐变疏。传感器测点位置见表2。

1.2.3 弯沉检测结果

弯沉检测结果通常受结构组合、各结构层厚度及模量、层间连接状态、沥青层温度、路基土湿度等因素影响，对于高速公路大修工程来说，还会受到通行区重型车辆通行的影响。为减少误差，提高弯沉值的可信度，特将采集密度设置为每50 m 1 个点，且不少于20 个点，记录每个测点的准确桩号和具体位置。由于检测时受气候和其他因素影响，只采集了C0至C6共7个传感器所在位置的弯沉值。汇总弯沉值时，采用“3σ原则”即(Xˉ-3σ，Xˉ+3σ)(其中，Xˉ为均值，σ为标准差)，对异常弯沉值进行剔除。旧混凝土板共振碎石化基层沥青加铺结构弯沉值如表3所示。旧混凝土板共振碎石化基层沥青加铺结构弯沉盆如图2所示。

弯沉值分析结果如表4所示。从表4可以看出：各个传感器所在位置的弯沉值变异系数均超过0.20。其原因可能是检测区域属于共振碎石化试验段，共振频率和行进速度等因素导致共振碎石化效果存在较大差异，进而导致检测弯沉值变异性增大。

表1 FWD荷载半周期加载变化量Table 1 FWD load half cycle load change

表2 FWD测点位置分布Table 2 FWD measuring point position distribution

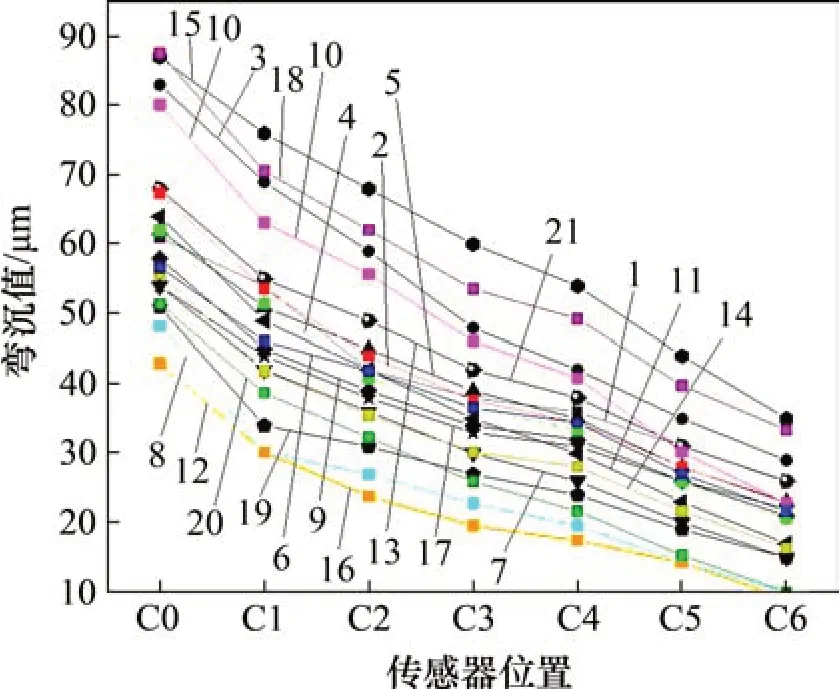
图2 共振碎石化结构弯沉盆Fig.2 Deflection values of deflection basin of resonance gravel structure

1.3 加铺方案及结构层划分

1.3.1 加铺方案

以G60 湘潭至邵阳高速公路大修工程项目为依托，收集大修工程中关于路面加铺结构设计、施工和交工资料，并进行现场调研，对FWD 路表实测弯沉值和模量反算弯沉值进行分析和汇总。经过比选提出旧混凝土板共振碎石化基层沥青加铺结构，如图3所示。

旧混凝土板共振碎石化基层沥青加铺结构各结构层的厚度和泊松比如表5所示。

1.3.2 结构层划分

结构层的划分对反算结果的影响很大，当层厚小于8 cm 或结构划分层大于4 层时，反算结果将出现很大偏差或导致迭代无法收敛，因此，进行模量反算时，需要合理地划分结构层。通常将模量接近的结构层作为1层进行结构划分。结构划分通常不超过4层，以3层结构为主。为减小反算误差，将结构划分为3层进行计算。

共振碎石化结构的自身特点为上部结构相互嵌挤的碎石粒料层、下部互相嵌锁的混凝土石料层，碎石粒度范围为3～20 cm，与级配碎石结构相似，基本参数按级配碎石的参数取值，与新加铺层材料弯沉值相差很大；同时，为了更好地反映新加铺层的结构模量，将共振碎石化层与水稳碎石层划为1层。旧混凝土板共振碎石化基层沥青加铺结构结构层划分如表6所示。

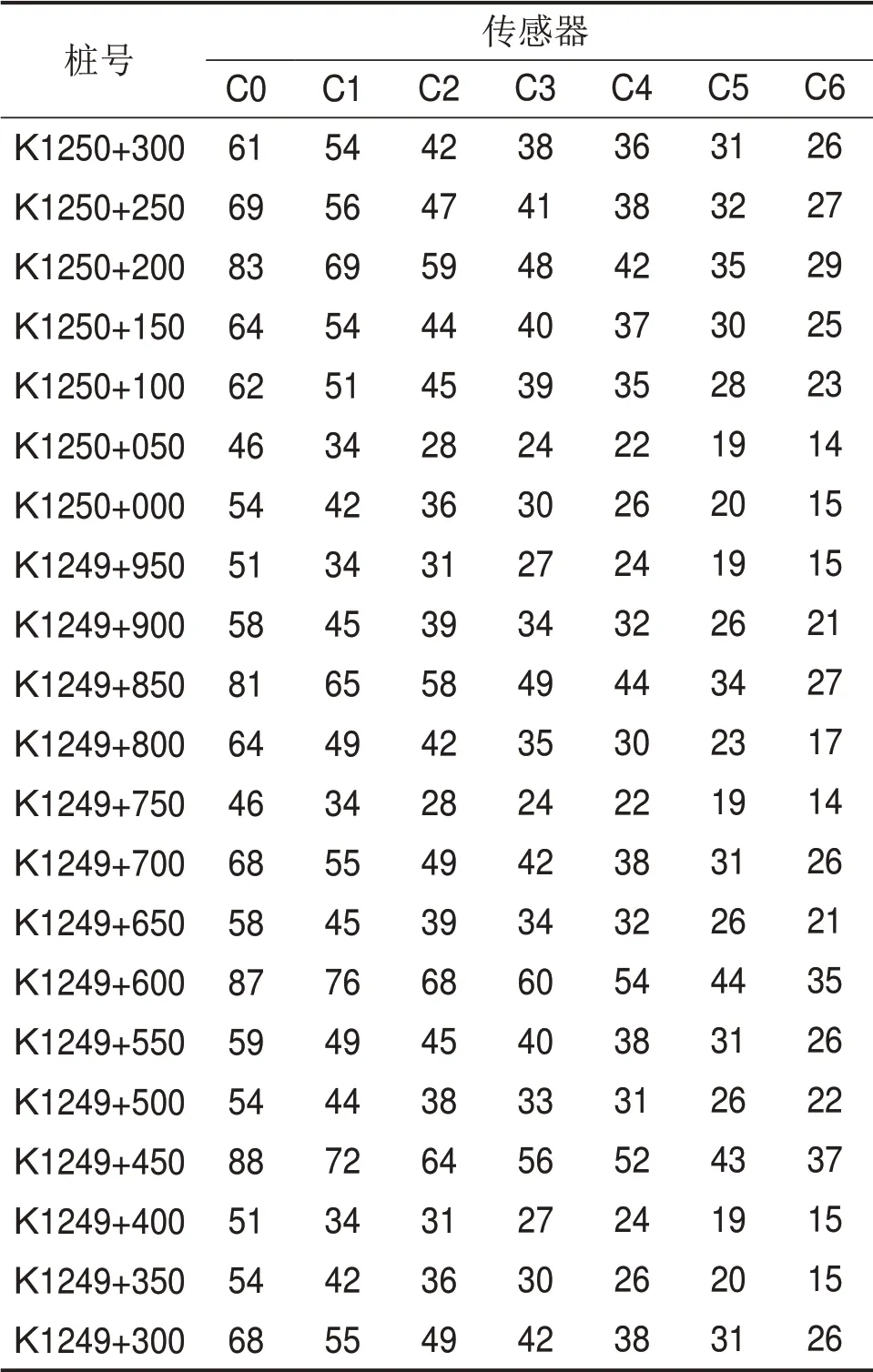
表3 弯沉值统计Table 3 Statistics of deflection values μm

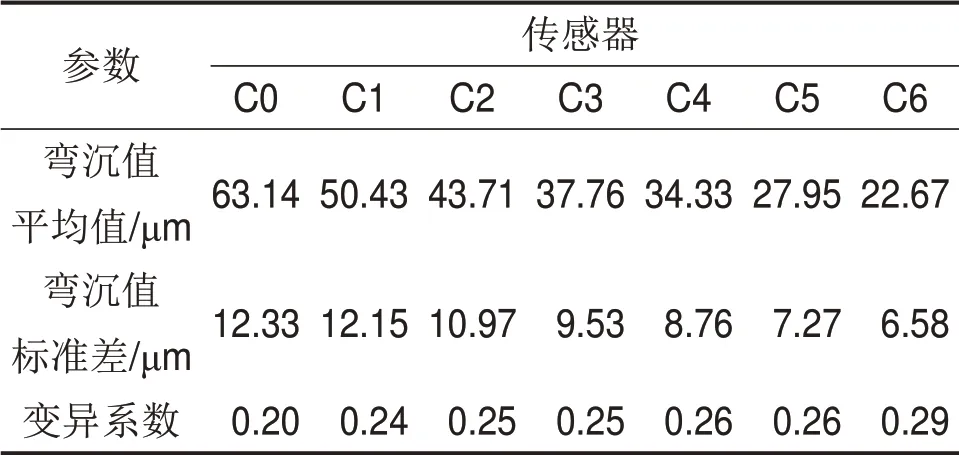
表4 弯沉值分析Table 4 Analysis of deflection values

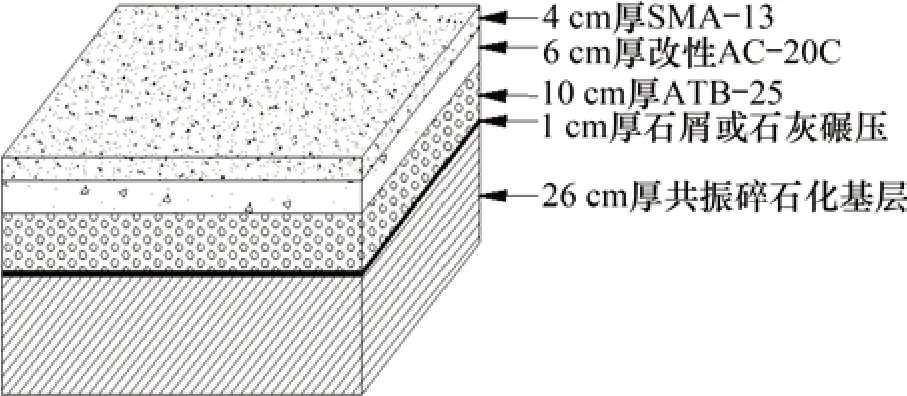
图3 旧混凝土板共振碎石化基层沥青加铺结构Fig.3 Asphalt overlay structure of old concrete slab resonance gravelized base

表5 旧混凝土板共振碎石化基层沥青加铺结构参数Table 5 Structural parameters of structural parameters of asphalt overlay of old concrete slab resonance gravelized base

表6 结构层划分Table 6 Structure layer division

2 沥青层平均温度计算

已有研究表明[12-15]，沥青混合料是一种感温性材料，各项性能受温度变化的影响较大，利用路面弯沉值进行模量反算时，需要对弯沉检测时的路面温度进行同步记录。为了更好地研究沥青层结构内部温度随深度的变化，国内外学者通过建立相应的预估方程对温度场进行预估。郑元勋[16]研究了基于FWD 的沥青路面弯沉值与路面温度间的相关关系，并建立了温度修正公式；李盛等[17]通过断裂力学理论和有限元法，计算并验证了CRC+AC 复合式路面中CRC 层最大温度梯度的准确性；付宏渊等[18]借助ABAQUS 计算了不同组合的路面结构温度梯度分布和车辙深度。国内外研究多以沥青层结构的平均温度作为代表温度，需要测定沥青层表面温度、中间温度和底部温度，然后取平均值。

2.1 有限元模型分析与验证

借助ABAQUS 有限元软件，根据已有某CRC+AC复合式路面温度建立模型进行计算分析。计算模型及主要参数取值如图4所示(其中，E为模量，μ为泊松比)，温度场计算参数如表7所示[19]。

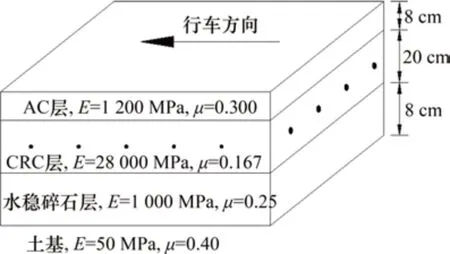
图4 计算模型示意及参数取值Fig.4 Schematic calculation model and parameter values

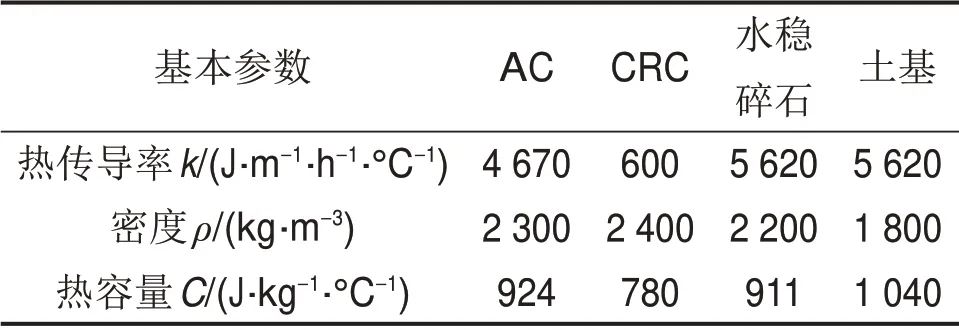
表7 温度场计算参数Table 7 Temperature field calculation parameters

根据传热学原理，借助ABAQUS 有限元软件并利用Fortran 语言子程序[17]对路面结构温度场实现有限元模拟。为了验证计算模型的可靠性，采用某地高速公路CRC+AC 复合式路面试验路的热学参数和采集温度，使用模型对温度场进行有限元计算，温度计算值与实测值对比如图5所示。

通过比较分析可知：温度计算值与实测值最大相对差为4.7%，表明所建立的计算模型精度较高，因此，用该模型计算沥青层表面温度、中间温度、底部温度是可行的。

2.2 加铺结构沥青层平均温度计算

旧混凝土板共振碎石化基层沥青加铺结构的温度场计算值按表7设置。弯沉参数采集时间为7:00—9:00，因此，输出7:00—9:00 时段有限元模拟得到的温度。在进行温度有限元模拟时，考虑到共振碎石化结构上部结构相互嵌挤的碎石粒料层、下部互相嵌锁的混凝土石料层，碎石粒度范围为3～20 cm，与级配碎石结构相似，因此，在进行有限元模拟时，输入的基本参数按级配碎石的基本参数取值，其中热传导率取6 734 J/(m·h·°C)，密度取2 100 kg/m3，热容量取920 J/(kg·°C)，太阳辐射吸收率、路面发射率和及Stefan-Boltzmann 常数与表7中的一致。旧混凝土板共振碎石化基层沥青加铺结构的计算模型及主要参数取值如图6所示。

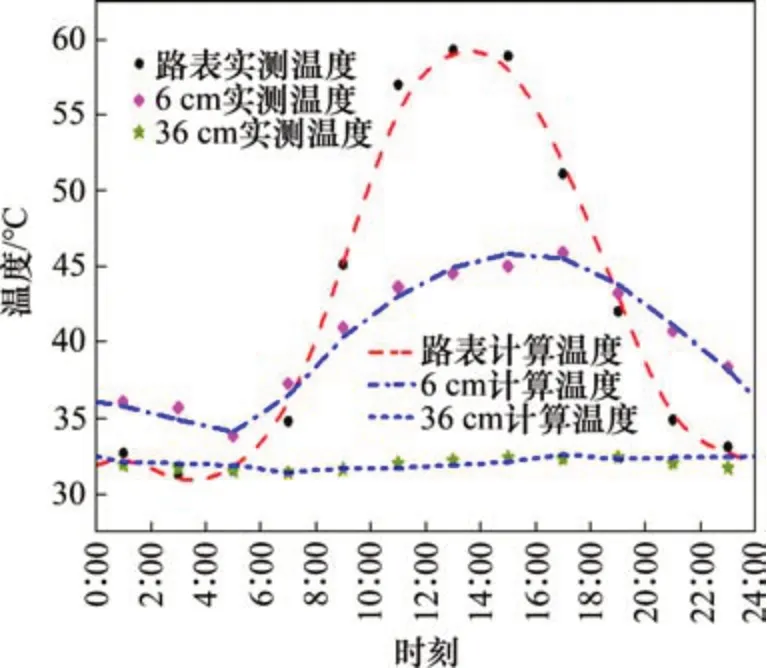
图5 不同深度下温度的计算值与实测值比较Fig.5 Comparison of calculated and measured temperature at different depths

图6 计算模型及参数取值Fig.6 Calculation model and parameter values

经过有限元计算得到路面结构中的节点温度云图如图7所示，温度云图输出的沥青层内部不同深度的温度变化规律如图8所示。

沥青层中间温度采用插值法计算，沥青层平均温度计算结果如表8所示。

3 旧混凝土板共振碎石化基层沥青加铺结构模量反算

根据采集到的动态弯沉值及有限元模型计算所得沥青层平均温度，并借助SIDMOD 及EVERCALC 模量反算程序对共振碎石化沥青加铺结构进行模量反算。

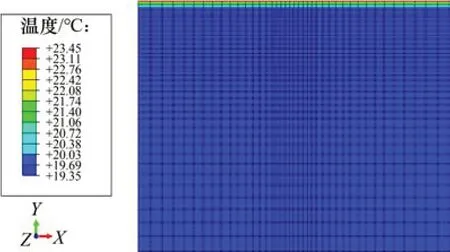
图7 路面结构中的节点温度云图Fig.7 Node temperature cloud diagram in pavement structure

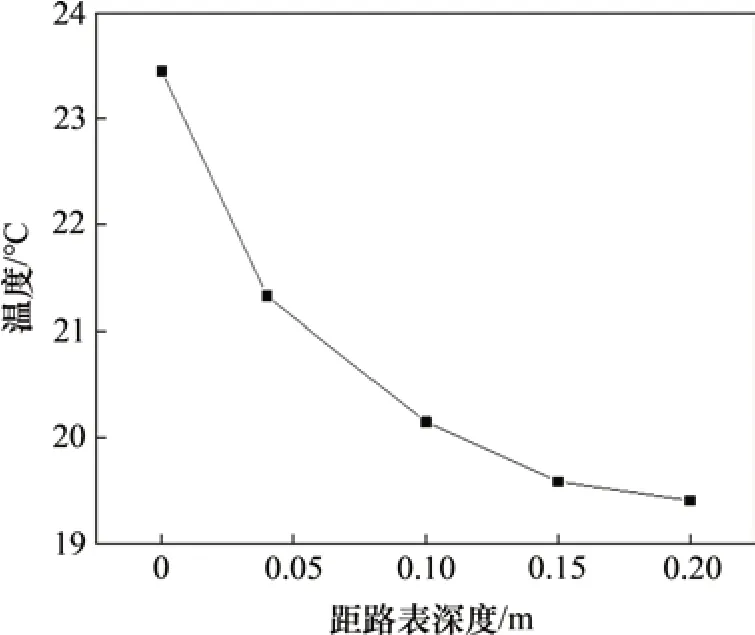
图8 沥青层内部温度随深度变化图Fig.8 Variation of internal temperature of asphalt layer with depth

表8 平均温度计算Table 8 Average temperature calculation

3.1 模量反算方法

3.1.1 SIDMOD程序反算

SIDMOD 程序属于迭代法的一种。迭代法的基本原理是首先根据路面结构实际情况对路面结构进行分层(2层、3层或4层)，然后，赋予各结构层模量(即初始值)，采用力学分析方法计算理论弯沉盆，并与FWD 实测弯沉盆进行比较，根据弯沉盆的差异确定模量修正值，从而获得一组新的模量。然后，以此作为下轮迭代的初始值，不断重复这一迭代过程，直至满足预先给定的收敛精度或迭代次数的要求为止。其优点是反算精度较高，且具有较好的扩展性。SIDMOD 程序的反算过程可用图9表示。

3.1.2 EVERCALC程序反算

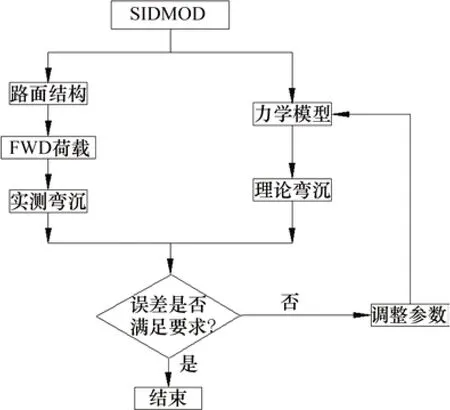
图9 SIDMOD反算流程Fig.9 SIDMOD inverse calculation processes

EVERCALC 程序也属于迭代法的一种。分层弹性理论的基本假设包括：水平方向上的结构层无限长；层厚均匀；底层在垂直方向上是半无限的；各层由均匀、各向同性、线性弹性材料组成，以弹性模量和泊松比为特征参数。

3.2 加铺结构模量反算及其分析

刚性下卧层是指位于土基一定深度之下具有较大刚度、对表面弯沉影响不可忽略的层位，刚性下卧层的埋置深度对模量反算结果的精度影响很大，特别是当埋深较浅时，影响尤为突出[20-22]。在模量反算时引入刚性下卧层，可以提高反演结果的精度和准确性。在计算过程中，要考虑不设刚性下卧层和设置刚性下卧层2种情况，其中设置刚性下卧层时，其深度取7.315 m，刚性下卧层模量取6 894.76 MPa，泊松比取0.50[23]。

旧混凝土板共振碎石化基层沥青加铺结构SIDMOD 和EVERCALC 程序模量反算结果分别如表9和表10所示。

对SIDMOD和EVERCALC程序模量反算结果进行处理并求均值，结果如表11所示。

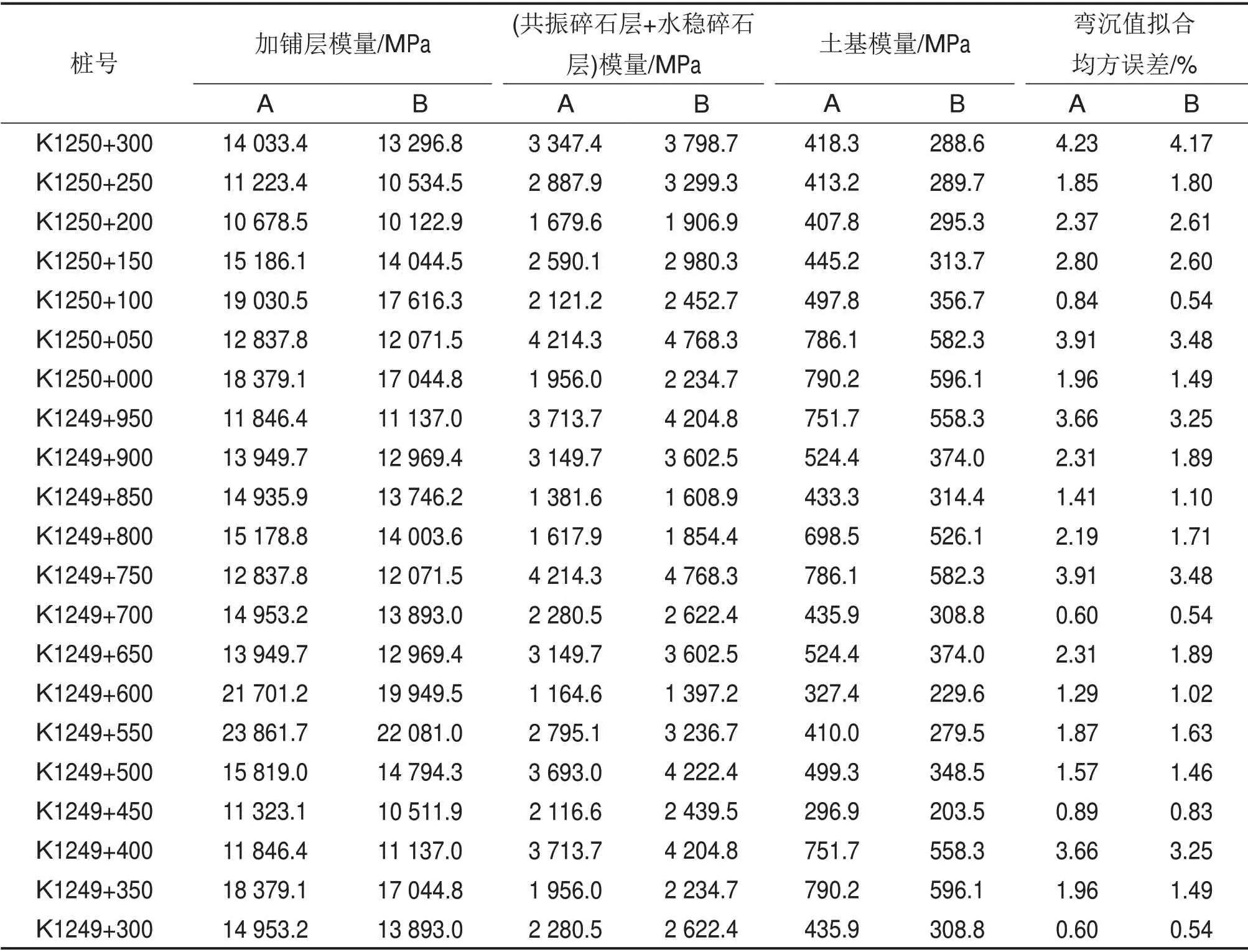
表9 SIDMOD程序模量反算结果Table 9 SIDMOD program modulus inverse calculation results

从表9和10 可以看出：与设置刚性下卧层相比，不设刚性下卧层时的3层体系中，上、下2层的模量均偏大，而中间层的模量偏小，弯沉拟合均方误差也偏大。中间模量偏低是因为反演时模型为多层半空间无限体，模型中土基顶面位置会比原路基顶面位置偏高，从而出现层间补偿作用。共振碎石机械在工作时除了对旧水泥混凝板产生作用外，对水稳碎石层和土基均存在不同程度的扰动和结构破坏现象，也会导致水稳碎石层和土基模量有所减小。从表11可以看出：SIDMOD 和EVERCALC 这2 种程序对旧混凝土板共振碎石化基层沥青加铺结构的模量反算结果显示良好的一致性。

3.3 三维有限元反演拟合

土基纵向是无限的，相当于没有设置刚性下卧层，故在有限元建模时选择使用SIDMOD 程序在不设刚性下卧层情况下反算得到的模量平均值，结果如表11所示。由于建模时对模型底部进行了X，Y和Z这3 个方向的位移为0(即U1=U2=U3=0)的约束，相当于设置了固定深度的刚性下卧层，故需对SIDMOD 程序反算得到的土基模量进行换算调整。对于路面大修设计，每个未黏结层的弹性模量可根据弯沉盆进行反算，或根据DCP 或CBR试验进行估计。若弹性模量通过弯沉盆反算所得，则这些值需要根据实验室条件进行调整。美国FHWA 设计手册[24]提供了设计中需要的调整系数，如表12所示。结构层参数如表13所示。

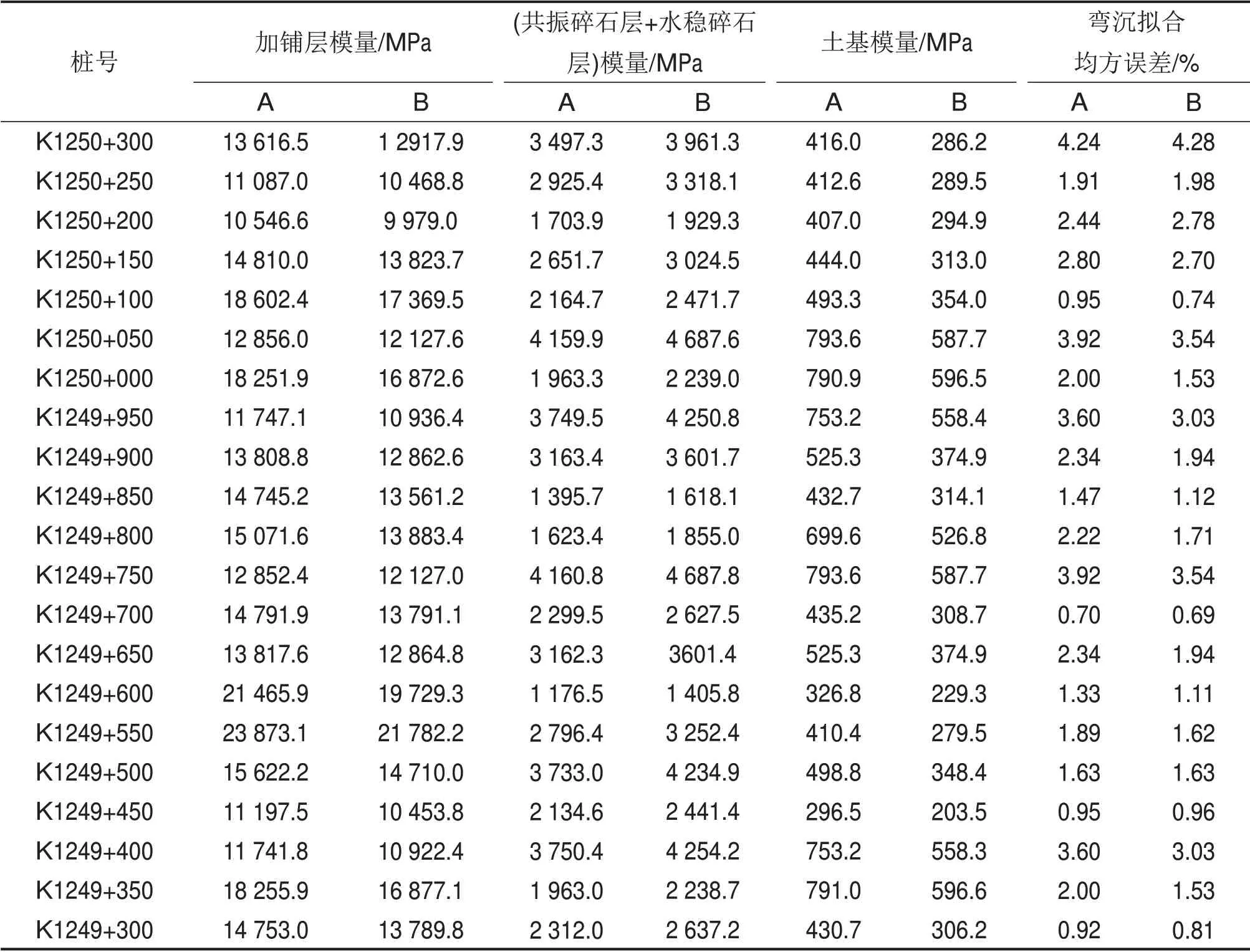
表10 EVERCALC程序模量反算结果Table 10 Calculation results of EVERCALC program modulus

表11 模量反算结果汇总Table 11 Summary of inverse calculation results MPa

模量调整公式为

式中：Mr为调整后的模量；C为调整系数；Mr1为反算得到的模量。

根据表13及式(1)，选取调整系数为0.35 对土基模量进行调整，调整后土基模量为190.4 MPa。

3.3.1 三维有限元模型建立

利用ABAQUS 有限元计算程序建立路面三维有限元计算模型，模型长×宽×高为10 m×10 m×11 m。模型共划分为3 层，结构层参数如表13所示。密度按表7进行设置；加载方式见表1，为半正弦函数动态加载。

采用C3D8R 三维线性八结点减缩积分进行建模，该单元能够较好地模拟各结构层的力学性能。网格划分时，在所研究的路面区域内将网格长×宽设置为0.2 m×0.2 m，加载区域网格长×宽为0.08 m×0.08 m，而将其他区域网格粗化(长×宽为0.6 m×0.6 m)。路面结构的三维有限元模型网格划分如图10所示。边界条件为：模型XZ两面各结点Y方向位移为零(即U2=0)，ZY两面各结点X方向位移为0(即U1=0)，Z方向底面各结点X，Y和Z方向位移均为0(即U1=U2=U3=0)，层间完全连续。

图10 路面三维有限元模型Fig.10 Three-dimensional finite element model of pavement

3.3.2 反演分析

以表12中的模量为初始模量，多次调整模型的模量输入值，直到有限元模拟弯沉值与实测弯沉值达到较高的拟合度为止。考虑到网格划分时对应的节点与落锤式弯沉仪并不是一一对应的，因此，尽可能多地选取节点的弯沉值与实测弯沉值进行拟合对比，从而选取拟合度较高的模量组合。

由于变形的滞后性，路表弯沉盆峰值出现在17 ms。当有限元模拟弯沉值与实测弯沉值达到较高的拟合度时，对应的有限元计算云图如图11所示。

表12 MEDPG模量调整系数Table 12 MEDPG modulus adjustment factors

表13 结构层参数Table 13 Structure layer parameters

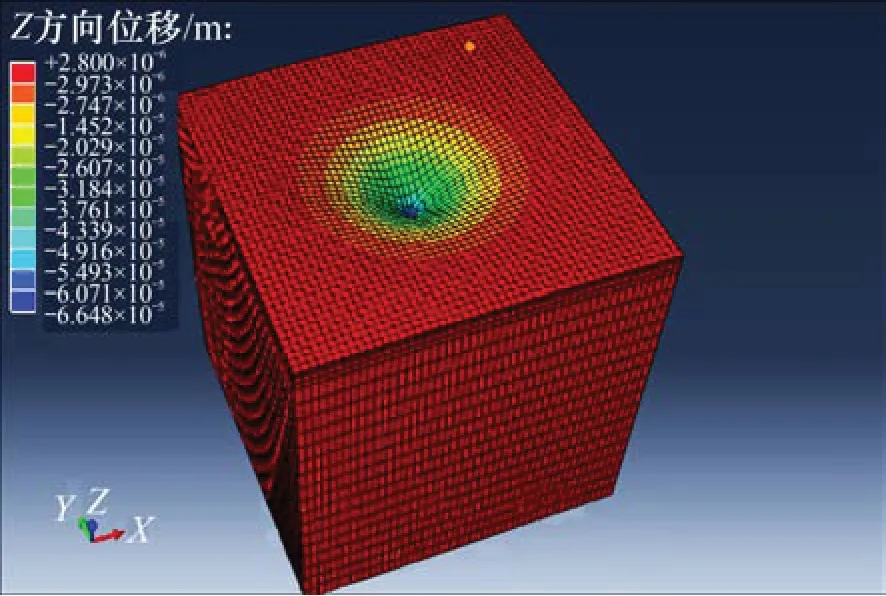
图11 17 ms时模型变形云图Fig.11 Deformation cloud map at 17 ms

各测点弯沉值如表14所示，有限元计算弯沉值和实测弯沉值对比如图12所示。

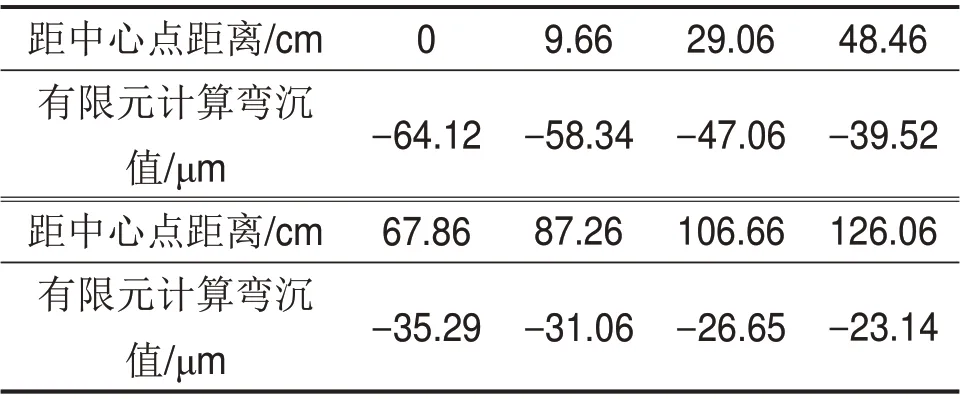
表14 17 ms时路表不同位置对应弯沉值Table 14 Deflection values at different positions on road table at 17 ms

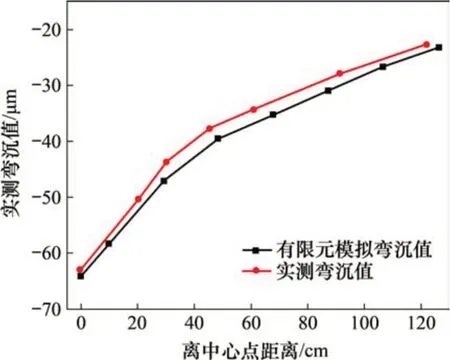
图12 有限元计算弯沉和实测弯沉值对比Fig.12 Comparison of calculated deflection and measured deflection by finite element

从图12可以看出：有限元模拟弯沉值曲线与实测弯沉值曲线比较接近，误差较小。有限元模拟弯沉值与实测弯沉值拟合度较高时对应的模量与反算所得的初始模量如表15所示。

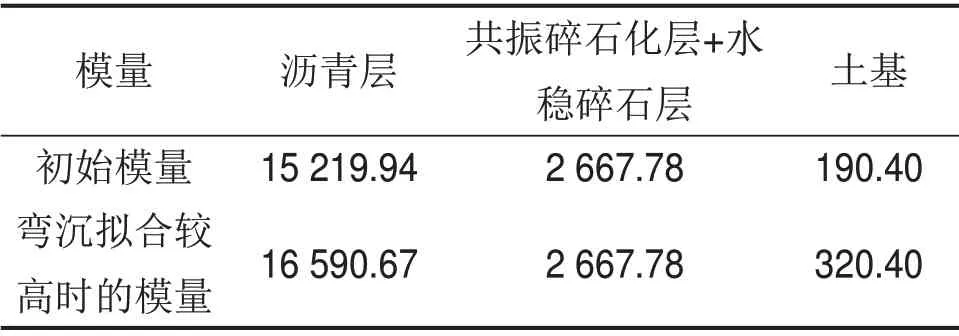
表15 有限元模型模量对比Table 15 Comparison of modulus of infinite model MPa

由表15可知：有限元模型反演确定的模量与SIDMOD 程序在不设置刚性下卧层时反算得到的模量相比，面层模量有所增加但变化较小；以SIDMOD 程序反算结果为初始模量建立模型，从输出的模量结果可以看出水稳碎石层模量未发生变化，沥青层模量有所增大但变化较小，也从侧面验证了SIDMOD程序反算结果的可靠性。