基于改进粒子群深度神经网络的频率域航空电磁反演
2020-10-09廖晓龙张志厚范祥泰路润琪姚禹曹云勇徐正宣
廖晓龙,张志厚,范祥泰,路润琪,姚禹,曹云勇,徐正宣,
(1.西南交通大学地球科学与环境工程学院,四川成都,611756;2.中铁二院成都地勘岩土工程有限责任公司,四川成都,610000)
1954年,频率域航空电磁法在加拿大应用于矿产勘探,并发挥了重要作用。经过60多年发展,该方法已广泛应用于基础地质调查、油气资源勘探及环境工程等领域[1]。频率域航空电磁的常用成像方法包括质心深度成像法[2]、微分电阻率成像法[3]等,此类方法可快速获得地下典型参数,但成像分辨率较低。为获得更加准确、定量化的地下电性信息,诸多学者对反演进行了研究,包括一维层状介质反演[4-6]、拟二维横向约束反演[7-9]和整体反演[10-11]等,这些研究极大推动了航空电磁反演的实用化,但此类方法依赖初始模型的选取,反演解容易陷入局部极小,对反演的准确性和稳定性有一定影响。近年来,完全非线性反演方法在地球物理数据处理解释中受到高度重视,此类方法对初始模型依赖小,无需计算灵敏度矩阵,有着良好的全局寻优性能。朱凯光等[12-13]研究了时间域航空电磁的神经网络反演;刘力辉[14]等采用深度神经网络进行地震岩相反演;奚先等[15]实现了散射波场的深度学习反演成像;师学明等[16]研究了大地电磁阻尼粒子群优化反演;柳建新等[17]将遗传算法引入大地电磁测深二维反演;胡祖志等[18-19]实现了大地电磁模拟退火反演及人工鱼群反演;殷长春等[20]采用变维数贝叶斯方法对频率域航空电磁资料进行反演。以上研究均取得了很好的成效,可见完全非线性算法在地球物理资料处理中发挥着重要作用,但这些算法的求解精度和收敛速度仍有提升空间。每种反演方法都有其优点及局限性,将不同反演方法的优势结合起来,通常能达到更好的反演效果。高明亮等[21]将免疫遗传算法与BP神经网络结合,实现了二维高密度电法数据反演;陈东敬等[22]使用带模拟退火的拟BP 神经网络反演重力资料;戴前伟等[23]结合粒子群优化算法与BP神经网络,进行了电阻率成像非线性反演;王鹤等[24]结合遗传算法与BP 神经网络,实现了大地电磁反演,取得了极好的效果。以上研究表明,混合优化算法能兼顾各方法优点,提高反演的精度与速度,保证反演的稳定性。基于此,本文将深度神经网络出色的局部寻优性能与改进粒子群优化算法良好的全局寻优能力相结合,提出了基于改进粒子群深度神经网络的频率域航空电磁反演方法。首先,阐述频率域航空电磁一维正演理论;其次,介绍改进粒子群优化算法优化深度神经网络的过程;第三,利用该方法对理论模型进行反演测试;最后,对实测航空电磁数据进行反演,并将反演结果与Occam 反演结果进行对比,以检验此方法的有效性。
1 频率域航空电磁1D正演理论
目前,频率域航空电磁系统主要采用水平共面装置[20],水平层状介质的回线源激发和接收模型如图1所示。根据NABIGHIAN[25],垂直磁偶源接收线圈的垂直磁场分量表达式为
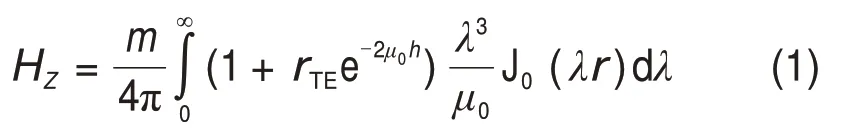
其中:
式中:Hz为总场;m为发射磁矩;rTE为TE极化的反射数;h为飞机的飞行高度;J0为零阶贝塞尔函数;r为接收线圈与发射线圈的距离;Yn为本征面波阻抗;Yˆn为本征阻抗;μn与σn分别为第n层的磁导率和电导率,通常认为大地磁导率等于自由空间的磁导率,即μn=μ0;ω为发射线圈发射角频率;kn为第n层的波速。
反演处理中所使用的是总场去除一次场并归一化后的数据[20]:
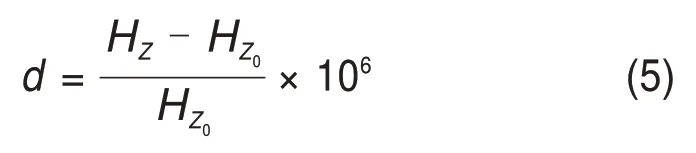
式中:HZ0为一次场;d为归一化垂直磁场分量。层状介质电磁响应公式含有零阶贝塞尔函数的广义积分,为保证计算速度与精度,本文采用快速汉克尔变换数值积分进行计算[26]。
2 改进粒子群深度神经网络反演
2.1 深度神经网络
深度神经网络(deep neural network,DNN),是近年兴起的一种学习能力极强的机器学习方法,在语音识别、图像识别及自然语言处理等领域应用广泛。它起源于传统的人工神经网络,具备更深的网络深度,能够融合各种非线性特征,具有强大的非线性学习和拟合能力[27]。

图1 频率域航空电磁层状介质模型示意图Fig.1 Schematic diagram of airborne EM layered medium in frequency domain
DNN 由多层自适应的非线性单元组成,每个神经层之间完全连接,通过逐层学习不断减小模型预测误差。图2所示为DNN 示意图,由图2可见:输入层节点数M由输入向量维数决定;隐含层节点数目与输入输出节点个数联系紧密;输出层节点数N由输出向量维数决定。
DNN的正向传播通过众多的神经元计算实现,工作过程可用式(6)和(7)来表示:

式中:xi为输入层第i个节点的输入;wji为输入层第i个节点与隐含层第j个节点的连接权值;θj为隐含层第j个节点的阈值;yj为隐含层第j个节点的输出;f为激活函数。常用有以下几种。
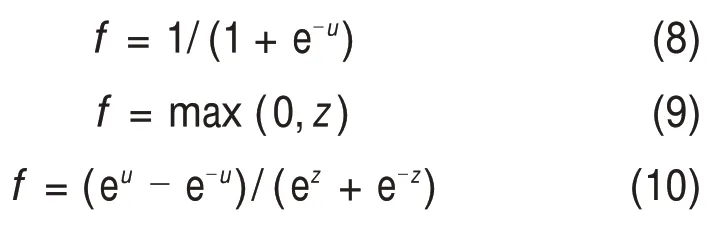
DNN 的反向传播过程即为网络的反向传播及自我修正过程,代价函数常有2种。


图2 深度神经网络示意图Fig.2 Schematic diagram of DNN
式中:di是训练数据的正确输出;M是节点的个数。式(11)为均方误差函数,式(12)为交叉熵函数。由于DNN 具有较多的隐含层,训练难度较大,为使代价函数达到最小值而避免陷入局部极值,常用随机梯度下降和Adam等优化方法[28]。
本文采用6 层全链接DNN 模型,代价函数选择均方误差函数,隐层激活函数使用ReLU 函数(能有效改善“梯度弥散”现象),输出层采用sigmoid激活函数。
2.2 粒子群优化算法
粒子群优化算法(particle swarm optimization,PSO)是KENNEDY 等[29-30]提出的一种智能优化算法,其基本思想源于对鸟类觅食的研究。假设在1个D 维搜索空间中,有m个粒子组成的集群X={X1,X2,…,Xm},第i个粒子的位置为Xi=(Xi1,Xi2,…,XiD),第i个粒子的速度为Vi=(Vi1,Vi2,…,ViD)。在粒子群优化算法迭代进化过程中,粒子会根据个体最优位置和群体最优位置不断调整自身移动方向,再到达下一位置。个体最优位置称为个体极值(Gbest),群体最优位置称为全局极值(Pbest),每个粒子移动的迭代公式如下[31]:
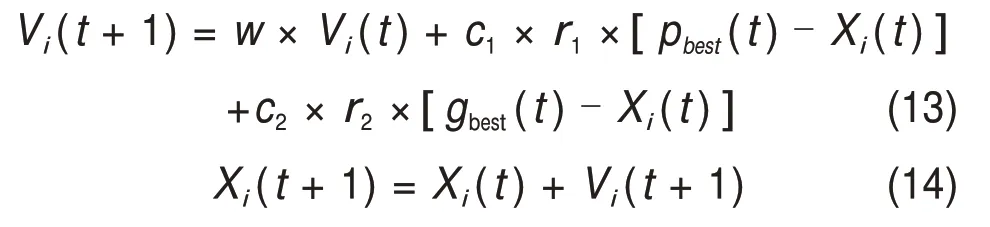
式中:t为进化次数;w是惯性权重;c1和c2分别为学习因子,一般取常数为2;r1和r2为[0,1]之间的随机数。惯性权重描述了上一代粒子速度对下一代粒子速度的影响,改变其大小可调节算法的全局寻优与局部寻优的能力。w较大有利于提高算法的全局寻优能力;w较小可增强算法的局部寻优性能。学习因子决定着算法的“自我认知”和“社会认知”能力,影响着种群靠近最优区域的能力。
2.3 改进粒子群优化算法优化深度神经网络
邵洪涛等[32-33]研究了粒子群优化算法的改进措施,取得了较好的效果。本文提出一种振荡衰减改进措施,即将惯性权值设置为

式中:ws和we分别为惯性权值的初值和终值;α为衰减因子;惯性权值w(t)随着迭代次数t振荡衰减。

图3 惯性权重迭代曲线Fig.3 Inertia weight iteration curve
惯性权重迭代曲线如图3所示,由图3可见:当迭代刚开始时,粒子的惯性权重取值较大,粒子将以较大的飞行速度寻找到全局最优解的范围,保证粒子群优化算法的全局搜索能力;在搜索的后期惯性权重取值较小,粒子的飞行速度较小,进而可以对最优解领域范围进行精确搜索,保证算法的局部搜索能力。同时,在搜索过程中,惯性权重振荡调整,可以不断改变粒子的速度与位置,增强粒子之间的信息交互,避免惯性权重减小导致算法陷入局部最优。
在求解复杂的非线性问题时,深度神经网络在设置初始权值时依赖于对样本空间反复试验,易产生网络不稳、收敛速度慢以及陷入局部最优等问题。而改进的粒子群优化算法具有良好的全局寻优能力,将其与深度神经网络结合,理论上可以寻找到求解问题的全局最优解。改进粒子群优化算法优化深度神经网络基本流程如图4所示。本文利用改进粒子群优化算法对深度神经网络优化步骤如下。

图4 改进粒子群优化深度神经网络流程图Fig.4 Flow chart of DNN optimized by IPSO
1)依据待解决问题,初始化深度神经网络,设定网络的输入层、隐含层和输出层神经元个数,并确定传递函数、学习函数和训练函数。
2)根据深度神经网络模型确定粒子的维数,使粒子每个维度分量对应神经网络的连接权值与阈值,并随机初始化粒子群。
3)计算种群中每个粒子的适应度fi。将每一轮最小适应度记为个体极值Gbest,将种群中所有粒子中最小适应度记为全局极值Pbest。
4)更新个体极值Gbest和全局极值Pbest。在每一轮迭代过程中,若粒子适应度fi小于Gbest,则Gbest=fi;若Pbest小于Gbest,则Pbest=Gbest。
5)根据式(13)和(14)更新粒子的速度与位移,采用式(15)惯性权重进行改进。按照粒子位置区间[Xmin,Xmax]和速度区间[Vmin,Vmax]规范超出限定范围的粒子。若满足迭代的终止条件,则进行下一步,否则返回步骤3)。
6)当达到迭代次数或目标精度时,选择最佳粒子作为深度神经网络的初始连接权值和阈值,然后进行网络训练,直到达到最大迭代次数或满足精度要求,算法结束。
3 模型试验
本文分别采用改进的粒子群深度神经网络(IPSO-DNN)、标准粒子群深度神经网络(PSODNN)和深度神经网络(DNN)对层状地电模型进行反演测试。设置参数如下:DNN 为6 层全链接方式(包含输入、输出及隐含层),其中隐含层4 层,节点数随训练数据集改变;粒子群规模20,进化次数200,学习因子c1=c2=2.0,PSO-DNN 算法惯性权值取0.8,IPSO-DNN算法惯性权值见式(15)。
3.1 2层地电断面模型
将正演得到的d值的实分量等距取20 个频点作为网络的输入,则输入层节点数为20;将2层地电断面模型的电阻率及厚度作为网络的输出,则输出层节点(ρ1,ρ2,h1)个数为3。为减少计算量,将电阻率与厚度值固定在一定范围,ρ1和ρ2取值范围为100~1 000 Ω⋅m,h1的取值范围为100~1 000 m,每个参数等距选择10个值,即ρ1与ρ2为100,200,…,1 000 Ω⋅m,h1为100,200,…,1 000 m。则模型总量为1 000组,将其中800组模型作为训练样本,200组模型作为测试样本,并对数据进行归一化处理。
利用IPSO-DNN,PSO-DNN 和DNN 算法分别对800组已知模型进行学习训练,图5所示为训练过程中均方误差(MSE)收敛曲线。由图5可见:DNN,PSO-DNN 和IPSO-DNN 算法起始反演结果均方误差分别为0.102,0.090 和0.079,说明改进粒子群优化算法降低了网络的初始误差;在训练过程中,IPSO-DNN算法在前20轮收敛速度极快,明显优于其余2 种算法,当训练至100 轮以后,PSO-DNN和DNN算法收敛速度极慢,计算已陷入局部极小,而IPSO-DNN 算法避开了此问题,100轮以后反演结果均方误差已小于0.010;当训练至200轮时,DNN算法的反演结果均方误差为0.038,PSO-DNN 算法的反演结果均方误差为0.025,IPSO 算法的反演结果均方误差为0.008,说明IPSO-DNN 算法在收敛速度及精度上均高于DNN和PSO-DNN算法。
对200组测试数据分别利用IPSO-DNN,PSODNN 与DNN 算法进行反演,并从中随机抽取10组数据的反演结果如表1所示,反演结果相对误差如表2所示。从表1和2可见:随机抽取的10组数据中IPSO-DNN算法反演相对误差明显低于其余2种反演方法的相对误差。为了更直观地展示反演结果,抽取一组G 型与D 型地电断面模型绘制电阻率-深度图,如图6所示。从图6可见:相比于PSO-DNN和DNN算法,IPSO-DNN算法反演出的电阻率和深度更接近真实模型。

图5 不同方法训练2层模型反演结果的均方误差收敛曲线Fig.5 MSE convergence curve of inversion for training two-layer model with different method
3.2 3层理论模型
采用3层水平模型进行研究,则网络输出层节点(ρ1,ρ2,ρ3,h1,h2)个数为5。令ρ1,ρ2和ρ3的取值范围100~1 000 Ω·m,h1和h2的取值范围为100~1 000 m,每个参数等间隔取10 个值,则模型总量为10×104。将其中80%(即8×104组)数据模型作为训练样本,其余20%(即2×104组)数据模型作为测试样本。利用IPSO-DNN,PSO-DNN 和DNN 算法分别对8×104组已知模型进行学习训练,图7所示为训练过程中均方误差(MSE)收敛曲线。由图7可见:DNN,PSO-DNN 和IPSO-DNN 算法起始均方误差分别为0.093,0.060和0.040,IPSODNN算法降低了网络的起始误差;在训练过程中,IPSO-DNN 算法前10 轮均方误差就已下降到较低值,相比之下,DNN和PSO-DNN算法收敛速度较慢;当训练至200 轮时,IPSO 算法的均方误差为0.016,PSO-DNN 算法的均方误差为0.024,DNN算法的均方误差为0.029,说明在3 层地电断面模型中,IPSO-DNN算法的收敛速度及精度也高于其余2种算法。
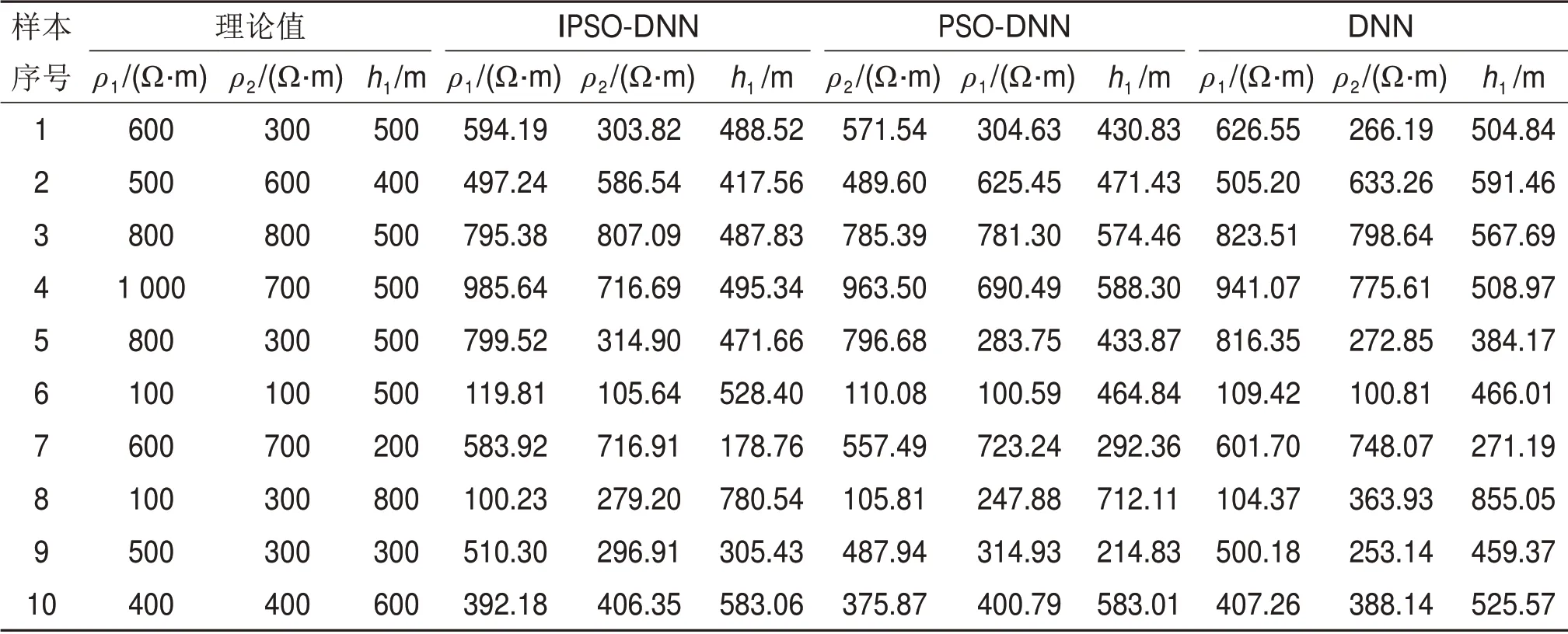
表1 2层模型10组数据不同方法反演结果对比Table 1 Comparison of inversion results of 10 sets of data for the two-layer model with different methods

表2 2层模型10组数据不同方法反演结果相对误差对比Table 2 Comparison of relative errors of 10 set of data for the two-layer model with different methods %
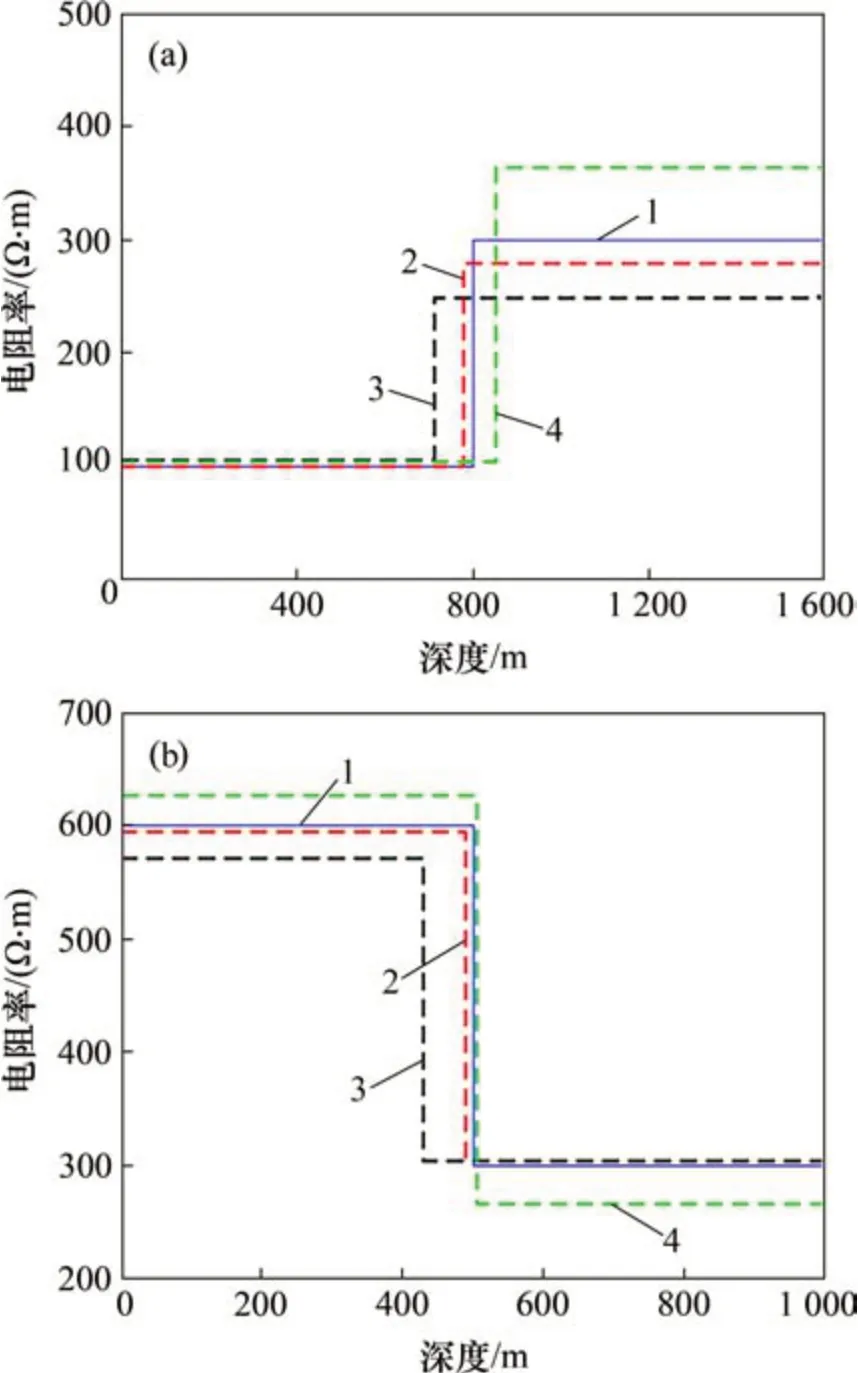
图6 2层理论模型不同方法反演结果对比Fig.6 Comparison of inversion results of the two-layer model with different methods
对2×104组测试数据分别利用IPSO-DNN,PSO-DNN 和DNN 算法进行反演,并从中抽取10组数据的IPSO-DNN反演结果如表3所示,相对误差如表4所示。由表3和4 可知:IPSO-DNN 算法的反演结果与理论模型的平均相对误差仅为4.53%,而PSO-DNN 和DNN 的平均相对误差均超过了10%。从表3中分别抽取A,H,K 和Q 型地电断面模型绘制电阻率-深度图,如图8所示,IPSO-DNN 算法的反演结果能更准确地接近真实模型。
3.3 不同程度干扰下的反演结果对比
为测试该算法在加入干扰后的适用性,本文在正演得到的测试集数据中加入了均值和方差均为零的正态分布随机噪声,含噪等级分别为3%,5%和10%。分别利用IPSO-DNN,PSO-DNN 和DNN 算法对3 种不同程度噪声水平的数据进行反演,并从中随机抽取了15 组反演结果,计算出与理论数据平均相对误差,如表5所示,由表5可见:在2层及3层模型的含噪数据反演结果中,不论噪声程度如何,IPSO-DNN算法反演结果相对误差均低于PSO-DNN 和DNN 算法;此外,噪声等级3%对各个方法反演效果的影响并不大。但随着噪声等级增加至5%和10%,PSO-DNN 和DNN 反演结果已出现较大误差,IPSO-DNN反演误差虽然也有增大,但误差增加幅度比PSO-DNN 和DNN反演算法的小,表明IPSO-DNN算法对于含噪数据具有更高的反演精度。
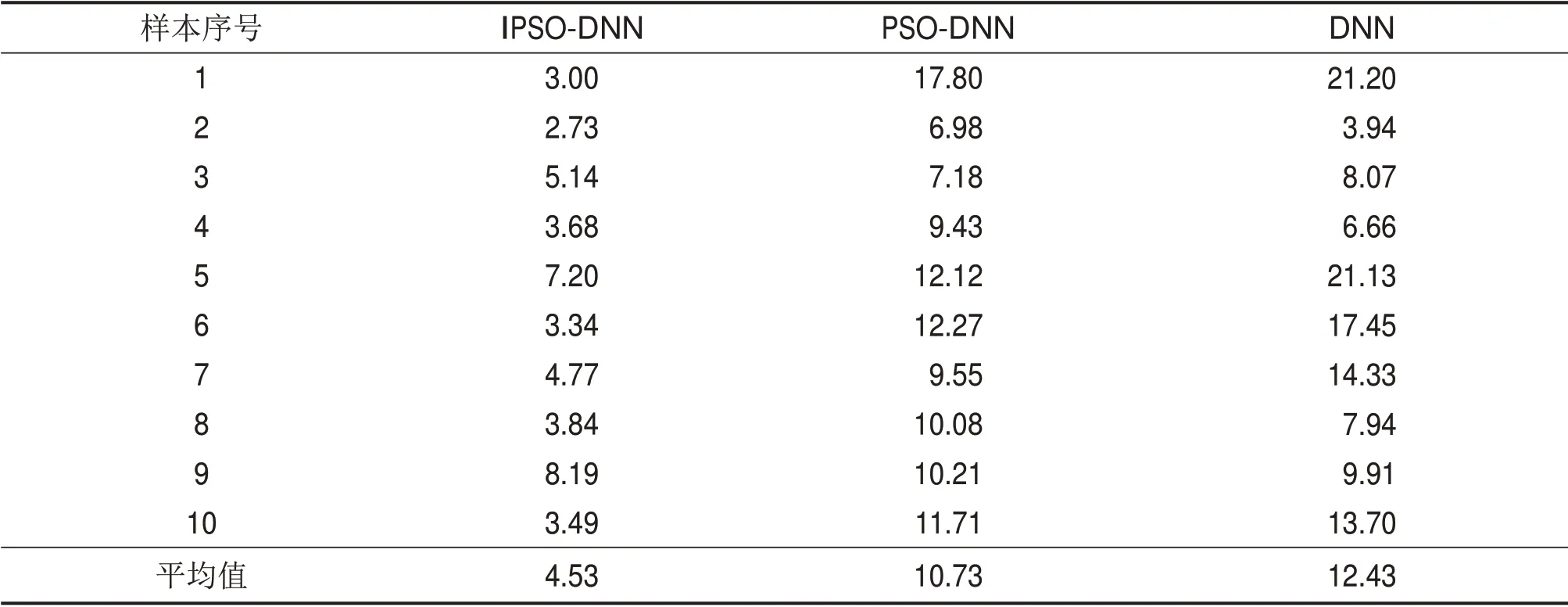
表4 3层模型10组数据不同方法反演结果相对误差对比Table 4 Comparison of relative errors of inversion results of 10 set of data for the three-layer model with different methods %
4 实测数据反演
利用IPSO-DNN方法对某地区近地表的实测航空电磁数据进行反演,验证该方法的有效性。实测数据为HCP装置测量的垂直磁场分量,共观测5个频点,分别为386,1 538,6 257,25 790 和100 264 Hz。根据该地区已知的地质资料及岩矿物性测定结果,确定了适合本地区的IPSO-DNN算法参数取值范围,并进行学习训练;再利用训练好的参数对实测数据进行反演,与Occam 反演结果进行对比。

图8 3层理论模型不同方法反演结果对比Fig.8 Comparison of inversion results of the three-layer model with different methods

表5 不同程度干扰下各方法反演相对误差对比Table 5 Comparison of relative error inversion of various methods under different degrees of interference%
图9所示为航空电磁实测数据Occam 反演结果。由图9可知剖面地层的连续性较好,地下电性结果大体分为3 层:第1 层电阻率为8~18 Ω·m,厚度约为10 m,经实际勘查确定为砂泥层;第2层电阻率为3~8 Ω·m,厚度约为10 m,确定为黏土层;第3 层电阻率为8~18 Ω·m,确定为含砂质地层。

图9 航空电磁实测数据Occam反演结果(据殷长春等[20])Fig.9 Inversion results of survey data with Occam's method
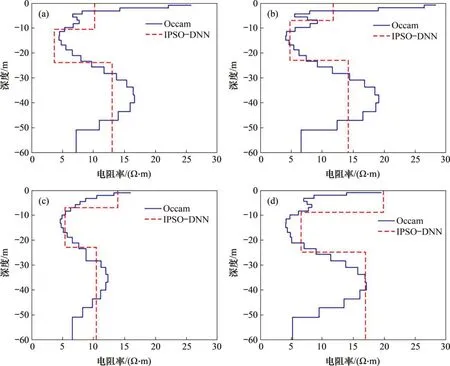
图10 航空实测数据IPSO-DNN与Occam反演结果对比图Fig.10 Comparison of inversion results of IPSO-DNN and Occam data from survey data
图10所示为4 个测点的IPSO-DNN 与Occam反演结果对比图,图10中的虚线为测点A,B,C和D(距离分别为25.7,157.7,288.2 和466.1 m)进行IPSO-DNN 反演的结果,实线为Occam 反演结果。由图10可见:2种方法反演结果变化趋势基本吻合,IPSO-DNN 算法的有效性得以验证。图10(d)中测点D的第1和3层反演电阻率与Occam反演结果有一定差异,说明此方法的预测结果与实际工区结果仍存在误差,需要考虑更多实际影响因素。
5 结论
1)将深度神经网络与改进粒子群优化算法结合,提出了改进粒子群神经网络反演方法,将该方法运用于频率域航空电磁反演,理论和实际结果均证明该方法的可行性。
2)改进粒子群深度神经网络算法结合了改进粒子群优化算法的良好的全局寻优性能与深度神经网络出色的局部寻优能力,有效避免了神经网络训练学习训练陷入局部极小等问题。相比于粒子群神经网络和单一神经网络,该方法具有更高精度与收敛速度;此外,改进粒子群深度神经网络算法对含干扰数据的反演效果也优于粒子群深度神经网络算法和单一的深度神经网络算法。
3)对于实测数据,受计算量的影响,需要了解测区相关地质资料以确定网络参数控制范围;为了减小实际资料反演误差,应考虑更多实际影响因素,建立符合实际地质情况的数据集。
