考虑非达西流固结土体中桩基承载时间效应研究
2020-10-09于光明龚维明戴国亮
于光明,龚维明,戴国亮
(1.东南大学混凝土及预应力混凝土结构教育部重点实验室,江苏南京,210096;2.东南大学土木工程学院,江苏南京,210096)
随着我国经济水平的不断提高,为满足发展需求,大量的高架桥梁以及跨江跨海大桥等配套基础设施正在兴建,许多位于滨海地区的工程面临着深厚软土地质条件,桩周土体随时间发生固结沉降。由于桩土相对位移,对桩基产生负摩阻力,增大桩基础的轴向荷载,严重影响桩基承载能力。
国内关于桩基负摩阻力问题自1980年开始受到关注,地面受到堆载和浸水等环境因素作用后,桩基下沉严重引起各类上部结构变形过大或破坏的案例较多,袁灯平等[1]总结了一些由负摩阻力引起的工程破坏案例;陈仁朋等[2]改进了桩土界面双曲线模型,基于桩侧土体初始剪切刚度随固结时间增长,分析了大面积堆载作用下不同固结度时桩侧负摩阻力发展规律;楼晓明等[3]采用数值分析的手段研究环形群桩基础在填土荷载作用下的负摩阻力和沉降特性;孔刚强等[4-5]基于一维非线性固结理论考虑了土体固结非线性特性,研究了桩侧负摩阻力分布特性,并且通过数值模拟分析楔形桩减小负摩阻力;贺成斌等[6]结合有效应力法与荷载传递法,建立了嵌岩桩负摩阻力分段模型;赵明华等[7]在桩基负摩阻力固结计算过程中考虑了地基土压缩模量沿深度变化的非线性特性;闫小旗等[8]开展了高填方夯实地基中桩侧负摩阻力试验,并采用荷载传递法计算了加固区和非加固区的桩侧摩阻力。前人关于桩周土体固结都是基于达西定律的经典固结理论,计算过程中没有考虑随着固结时间推移土体有效应力的动态变化。
实际上,由于土体在水力梯度较低[9]时,流速与水力梯度呈非线性关系,当实际水力梯度超过流动孔隙水最大结合能所对应的水力梯度时,土体的流速与水力梯度呈线性关系。考虑到土体固结过程中非达西流动定律更符合实际情况,本文基于非达西流动流速计算公式[9],考虑固结过程中桩周土体渗透系数和有效应力等变化,提出了非达西流动固结土体中桩基长期承载时间效应计算方法,考虑了固结过程中桩基下拉荷载和中性面位置的动态变化,分析了不同排水条件下摩擦桩和端承桩下拉荷载分布及中性点变化规律。
1 桩土相互作用力学模型建立
1.1 力学假定
在计算过程中做如下假定:
1)桩周土在固结前为均质和各向同性;
2)孔隙水按不可压缩材料考虑,水的排出仅发生在深度方向,水平方向不计;
3)土颗粒不考虑蠕变特性,桩周土沉降只因水的排出导致;
4)桩侧剪应力在微段均匀分布,则桩身微段的轴力沿深度按线性分布;
5)桩体材料按照理想弹性体考虑。
1.2 桩侧剪切函数
RANDOLPH 等[11]提出桩周土体的变形可以假定为理想同心圆的剪切破坏,关于桩土相对位移存在如下关系:
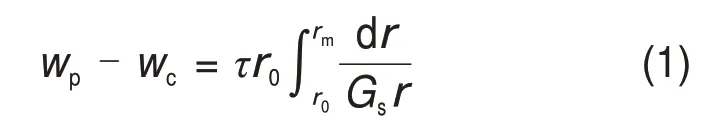
式中:τ为剪切力;Gs为桩周土的剪切模量;wp为桩身变形;wc为桩侧土固结沉降;r0为桩的半径;rm为最大影响半径。
对于摩擦桩,RANDOLPH 等[11]提出按照式(2)计算
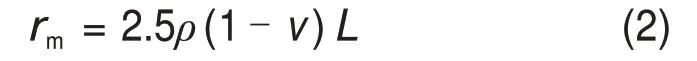
式中:v为桩侧土体泊松比按深度加权的平均值,υ=υsiLi/L;L为桩嵌入土体的深度;Li为第i层土层厚度;ρ为非均匀系数,体现桩身中部与桩尖处桩侧土剪切模量的比值,为桩嵌入深度范围内剪切模量平均值,为第i层土的剪切模量;Li为第i土层厚度;GL为z=L处桩周土的剪切模量。
对于端承桩[12],最大影响半径可由式(3)计算
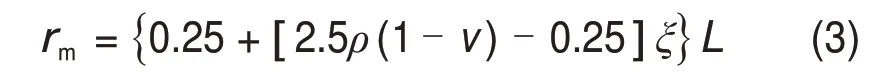
式中:ξ为桩尖处桩侧土体剪切模量与桩端以下土体剪切模量的比值,ξ=GL/Gb;Gb为桩端土的剪切模量。
ALONSO 等[13]认为当桩侧摩阻力小于极限剪应力时,作用在桩身的剪应力τ是桩土相对位移的函数,将式(1)积分求解可得
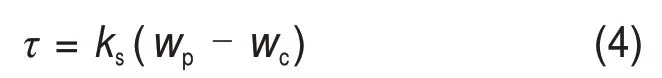
式中:ks为桩侧剪切刚度,ks=Gs/r0ln(rm/r0)。
1.3 桩土界面单位极限侧阻力
桩周土体随时间发生固结变形引起桩身变形,当桩土相对位移超过某一极限时,在给定深度处土体沉降和相邻桩节点的变形不再同步下沉。这意味着桩土界面发生塑性滑移,在这种情况下,桩侧阻力达到桩土界面剪应力极限。桩土界面极限剪应力τf可通过BJERRUM 等[14-15]基于土体有效应力原理提出的β法计算。
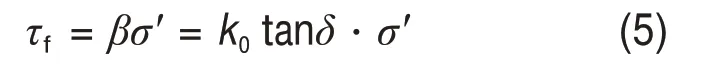
式中:σ′为土体竖向有效应力;k0为静止土压力系数;δ为桩土界面摩擦角,δ=κ⋅φ′,φ′为土体内摩擦角;κ为考虑界面强度参数相比土体强度降低的折减因子,对于无涂层桩取2/3,对于有涂层桩取0.15[16]。
2 考虑非达西流动定律的桩周土固结沉降
2.1 非线性固结方程推导
对于正常固结均质土,孔隙比与有效应力在半对数空间e-logσ′呈线性关系[17-18],曲线斜率称为压缩指数Cc。在孔隙比和渗透性[19-20]之间也呈线性相关,对应曲线斜率为渗透率指数Ck,两者计算公式如下
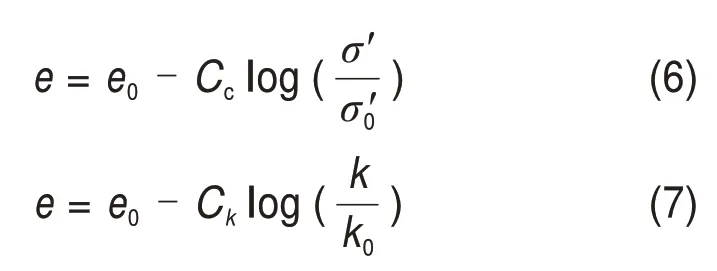
式中:σ′,e和k分别为土体的有效应力、孔隙比和渗透系数;σ′0,e0和k0分别为土体的初始有效应力、初始孔隙比和初始渗透系数。
在水力梯度较低时,土体流速与水力梯度呈非线性关系,当超过某一数值后才呈现线性关系,根据DUBIN 等[10]提出的非达西流动方程来计算流速。
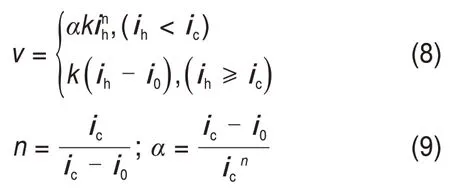
式中:ih为水力梯度;i0临界水力梯度;ic为启动压力梯度,根据HANSBO[21]的解释,启动压力梯度是能够克服流动孔隙水最大结合能的一个界限水力梯度;n和α分别为非达西定律的拟合参数;v为流体通过土体介质的流速。
固结过程中土体体积的变化率等于孔隙体积的变化率。

式中:V为土体单元体积;Vs土体颗粒体积;t为时间。
对于孔隙比e有如下关系

式中:av为压缩系数;u为超孔隙水压力。

将式(11)和(12)代入式(10)中可得
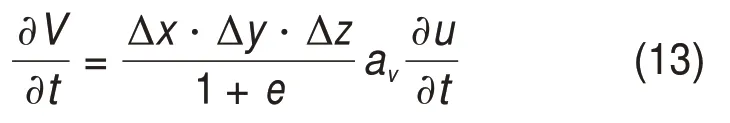
由于压力梯度,水流经过孔隙并逐渐流向排水面,单位时间内单元体的排水量为
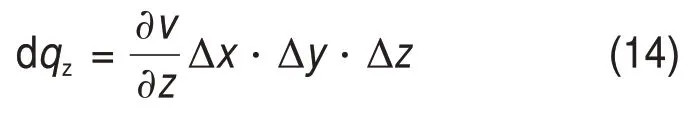
式中:dqz为z方向的单位渗流量微分形式。
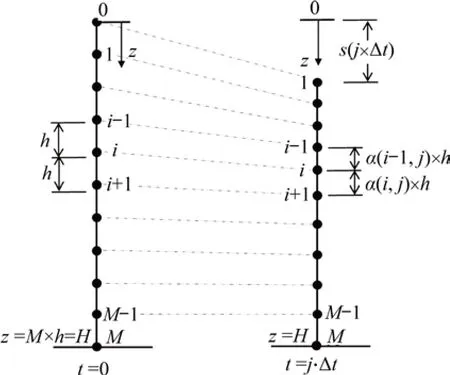
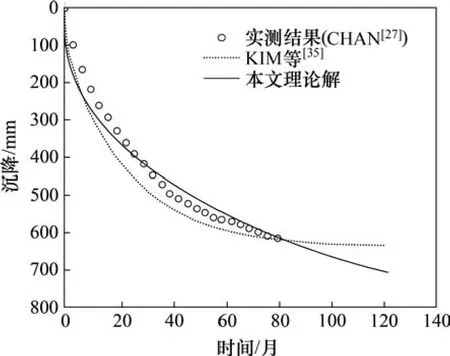
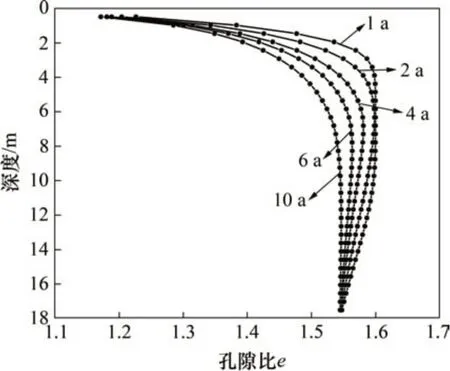
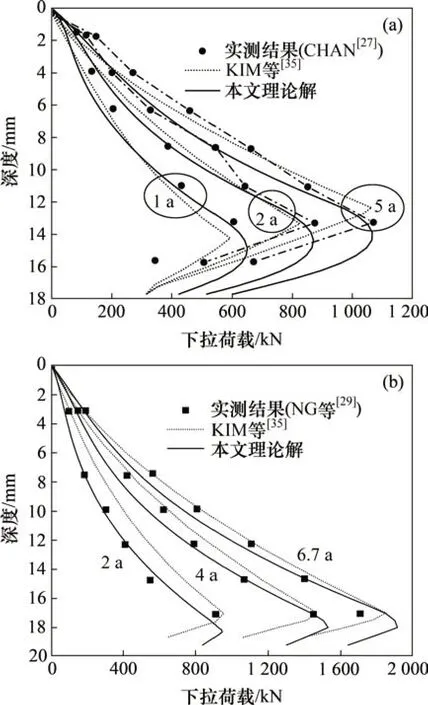
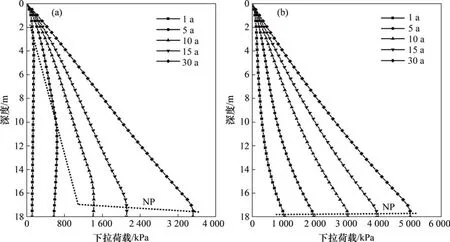
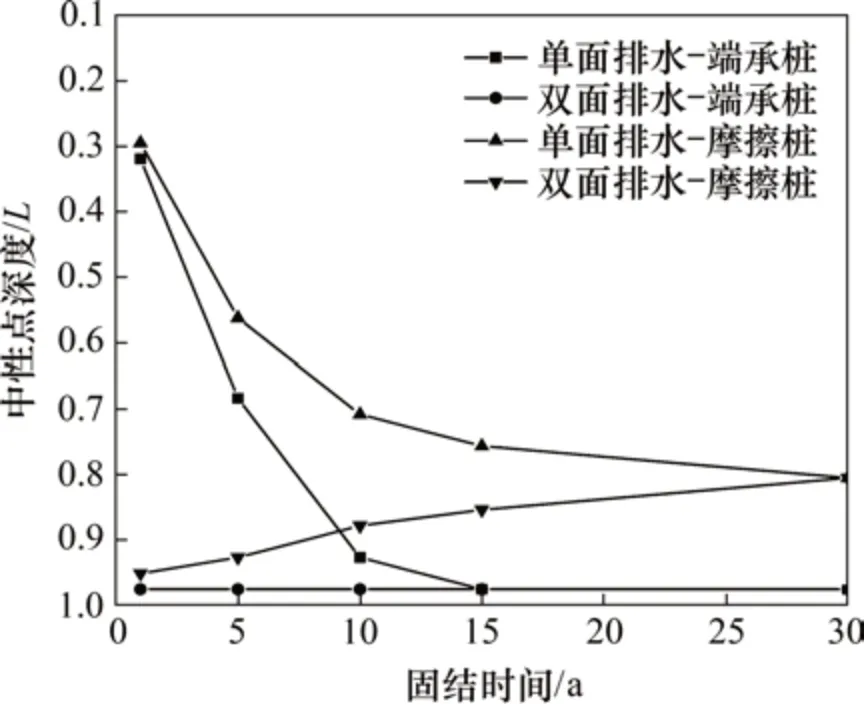
考虑0 ≤ih 水力梯度与土层中的超孔隙水压力梯度有关,表达如下 式中:γw为水的重度。 将式(16)代入式(15)后改写为 计算点处土体微单元的体积为V=Δx⋅Δy⋅Δz,在一维固结情况下,土体单元中水的流动仅沿竖直方向,土体单元水的流入流出速率差等于土体单元体积变化率,由式(13)与(17)相等关系可知式(2)联合后变为 固结系数Cv计算公式为 将式(20)代入式(19)可得 采用中心差分方程对式(21)中的渗透系数和超孔隙水压力关于时间和空间的偏导数进行替换后变为 式中:ui,j为固结土层深度方向第i点在时间j时的超孔隙水压力;ki,j为固结土层深度方向第i点在时间j时的渗透系数;h为土层微段厚度;Δt为时间增量。 采用类似的推导方法可以获得当ih≥ic时的超孔隙水压力差分求解公式,这里不再赘述。 在利用式(22)和(23)求解超孔隙水压力时已知初始边界条件如下。 土层排水条件为单面排水时, 土层排水条件为双面排水时, 式中:q为地表堆载。 在确定时间增量Δt和深度单元长度h时,要保证满足数值稳定性和精度的要求才能进行求解,根据FORSYTHE 等[22]的研究可以确定式(22)和(23)解的稳定性标准。 考虑土体固结过程中土体有效重度γ′随时间变化,根据有效应力原理,给定深度z处的有效应力为 式中:σ′(z,t)和u(z,t)分别为深度z处土体在t时刻的有效应力和超孔隙水压力;e(z,t-1)为深度z处土体在t-1 时刻的有效应力;Gs1为土粒相对密度。 土体自然对数应变[23]的微分表形达式积分后有 图1所示为不同时刻差分沉降示意图。针对一个微小区段引入长度折减因子α(i,j) 图1 不同时刻差分沉降示意图Fig.1 Schematic diagram of differential settlement at different time 则j时刻土层顶面沉降用折减因子来表示为 式中:H为土层厚度。 桩顶受到均布轴向应力p作用,则桩顶荷载为Q=p⋅Ap,桩身轴向荷载和桩单元变形可以如下建立平衡方程 式中:P(z)为深度z 处桩身轴力;wp(z)为桩的压缩变形;Ep为桩弹性模量;Ap为桩的横截面面积。 桩身离散为n段,编号依次为0,1,…,i,…,n。假定每个桩单元摩阻力均匀分布,则桩单元轴力按照线性分布,第i桩单元压缩变形可以通过对式(32)进行积分获得。 对于桩单元而言,求解式(35)可得桩身变形和轴向荷载的关系: 式中:wp(i)和wp(i+1)分别为桩节点i及节点i+1的竖向变形,i=0,1,2…,n-1;P(i)和P(i+1)分别为桩单元第i和i+1 节点的轴力;h为桩单元长度。 基于桩的轴力和桩侧剪应力关系,桩体平衡方程可表达为 桩侧摩阻力的合力等于桩单元首末两端节点的轴力差,则式(35)可以转换为 外荷载沿着桩身向下传递,桩侧阻力没有抵消的剩余荷载被传递到桩端土体,在桩端存在以下边界条件 式中:pb为桩端轴力;wpb为桩尖沉降;wcb为桩端位置处相邻节点的桩周土沉降;αb为桩端承载力水平系数,αb=Rfpb/pfb;Rf为破坏比,Rf=τf/τult;可以在0.80~0.95取值[24];τf为桩土界面剪切强度;τult为桩土界面极限剪切应力。 桩端极限承载力与桩端土体力学性能、截面积及桩端平面位置处桩侧平均竖向压力有关,可以按下式计算。 式中:Pfb为桩端极限承载力;cs为桩尖以下土体黏聚力;Nc和Nq的计算方法分别参考文献[25]和[26],即Nq=tan2(π/4+φ/2)⋅eπtanφ,Nc=(Nq-1)cotφ;Ab为桩端横截面面积;φ为桩端土的内摩擦角;为桩端平面处桩侧平均竖向压应力,=(1+2k0)L/3;为桩端以上土体的平均有效重度;k0为静止土压力系数。 在桩周土固结期间,对于任意给定时间t,都可以通过假定桩顶沉降并联立式(4),(34)和(36)以及边界条件进行循环迭代求解,获得所有桩节点的侧摩阻力、桩身变形以及轴力。 为验证本文理论方法的可行性,通过与CHAN 等[27-28]及NG 等[29]所做回填堆载作用下桩顶自由单桩离心机试验结果进行对比,监测了土体固结过程中单桩下拉荷载的变化,加速度为60g(g为重力加速度),土体和桩的几何尺寸都放大为模型几何尺寸的60倍。 试验1 为端承桩,将铝制单桩打入18 m 的饱和软黏土中,桩尖嵌入底端砂层0.25D(D为桩径),试验2 为摩擦桩,将17.7 m 的桩打入饱和软黏土,桩尖位于底部密砂层以上3.0 m处。 桩外径为1 140 mm,壁厚为90 mm,内径为960 mm,桩身弹性模量E为70 GPa,在桩体打入完成后在地表回填3 m厚砂子作为表面堆载并作排水面,回填砂重度为15 kN/m3,相当于45 kPa的荷载作用在地表面。其他参数根据实测资料进行估计,黏土的初始孔隙比取1.6,黏土的剪切模量取2.4 GPa,泊松比为0.35;持力层砂土的剪切模量取38 GPa,泊松比为0.3。计算过程中由于试验模型桩为管桩,采用刚度等效原则,将管桩转换为实心桩,EA=EeAe,换算后桩半径不变,桩的等效弹性模量为20.36 GPa。根据试验结果观察到黏土饱和重度在离心试验前后分别为16.3 kN/m3和16.7 kN/m3。黏土初始渗透系数为0.13 m/a,根据DRNEVICH等[30-31]的研究,压缩指数Cc=0.234 3e0,根据TAVENAS 等[32-34]研究结果,软黏土渗透指数Ck=0.5e0,非达西固结指数为1.25,启动压力梯度为10,将18 m厚黏土划分为37段。每段厚度不到0.5 m,时间步长为0.25 d。 KIM 等[35]计算时,基于达西定律将各土层初始有效应力按土层中点统一取相同值,不随深度发生改变。若本文将非达西固结指数取1,即演变为达西流动,并将初始有效应力设置为相同数值,经过对比发现:本文结果与KIM 所计算的土体沉降、超孔隙水压力分布曲线非常接近,验证了本文程序的正确性,由于篇幅限制这里不再赘述。 如图2所示为土体固结过程中试验1实测地表沉降随时间变化曲线与预测结果对比。由图2可见:本文理论解与试验发展趋势非常接近,在固结80月后本文计算所得地表沉降为613 mm,实测结果为615 mm。本文结果与Kim 等[35]的计算结果相比,在固结开始到10月之间两者较为接近,10~80月本文计算结果更小,80月之后本文理论计算所得地表沉降则更大,本文计算结果与实测地表沉降发展趋势接近。 图2 实测沉降与计算沉降对比曲线Fig.2 Comparison curves between measured and calculated settlement 图3所示为超孔隙水压力和有效应力计算结果对比。由图3(a)可见:采用非达西流动定律计算的土层超孔隙水压力消散速度比达西流动计算的超孔压消散速度慢,由于是双向排水条件,在上下2个分界面开始水流逐渐排出,消散区域慢慢向土层中间扩散,总体而言中间消散速度最慢,呈抛物线形式分布。KIM 等[35]的计算结果中超孔压最大值位于地面以下7.6 m处,本文理论解位于地面以下6.3 m,形成该现象的原因是考虑土体自重的影响后,超孔隙水压力朝向端部消散的速率要比朝地表方向的更快。固结1,2和5 a后,超孔隙水压力最大值分别为45,44 和37 kPa,KIM 等[35]按照达西流动计算的结果可以看出固结1,2 和5 a后,超孔隙水压力最大值分别为39,26和6 kPa。 由图3(b)可见:由于土层边界水流较快,超孔隙水压力消散最快,因此在0~2 m段有效应力沿深度逐渐减小,在2 m到土层下边界之间有效应力沿深度逐渐增大。经过对KIM 等[35]的计算结果进行对比,发现虽然土层初始有效应力取固定值即平均有效应力,但分析的有效应力图中结果是用实际初始有效应力减去超孔隙水压力,因此,可以与本文计算结果按照达西流动和非达西流动的方式进行对比。本文计算结果总体而言比达西流动计算结果小,这会导致土体的固结过程如果按照达西流动定律计算,根据有效应力原理分析的土体有效应力、桩土界面强度均会被高估。 如图4所示为不同固结时间的土体沉降沿深度变化曲线。由图4可见:沉降具有明显的非线性特性,固结初期1~2 a 内,深度2 m 以上土体沉降最大,2 m 以下沉降较小,固结5 a 之后,因为排水过程中超孔隙水压力消散,土层沉降明显增加。与KIM 等[35]结果相比,本文理论解得到的土层沉降在浅层更大,深部较小。 图4 土体沉降沿深度变化曲线Fig.4 Change curve of soil settlement along depth 如图5所示为固结过程中孔隙比沿深度变化曲线。由图5可见:在浅地表部分孔隙比急剧减小,这是因为浅地表有效应力较小,超孔隙水压力的消散量级对此处土体固结后有效应力与初始有效应力比值影响显著;下边界孔隙比减小幅度较小;越靠近土层边界,排水速率越快,土体的孔隙比就更早达到稳定,在土层中部孔隙比达到稳定的速度最慢。总之,在非达西流动定律下的固结计算过程中孔隙比减小速度由中间部分向上下两边界逐渐增大。 图5 固结过程中孔隙比沿深度变化曲线Fig.5 Variation curve of pore ratio along depth during consolidation 如图6(a)所示为摩擦桩实测下拉荷载与预测结果对比,摩擦桩中性面位于桩尖以上大约3.4 m位置,在固结1,2及5 a后桩身中性面处最大下拉荷载本文计算值分别达到641,870 和1 065 kN,而对应的实测下拉荷载分别为604,874 和1 070 kN,KIM 等[35]的计算结果分别为593,825 和1 063 kN,计算值与实测数据比较接近。 如图6(b)所示为总长19.2 m的端承桩实测结果与本文理论计算结果对比,端承桩中性面位于桩尖以上大约1.2 m 平面处,在固结2,4 及6.7 a 后中性面处下拉荷载计算值分别为921,1 530 和1 914 kN,对应实测值分别为908,1 449 和1 707 kN,KIM 等[35]的计算结果分别为951,1 469和1 850 kN,计算值与实测数据比较接近。桩身形成的下拉荷载由桩端土承担,端承桩与摩擦桩下拉荷载相比较而言,摩擦桩由于桩端土较软,不能为桩基提供足够的抗力,因此,摩擦桩的桩尖下沉量比端承桩大很多,其中性面位置距离桩端土顶面比端承桩更远,这导致了端承桩下拉荷载总体都比摩擦桩的下拉荷载大的多。 为研究堆载作用下软土在不同排水条件的沉降对桩基础下拉荷载分布的影响,将18 m 长混凝土桩穿过软黏土层,桩径为1.5 m,桩身弹性模量为31.5 GPa,桩端分别支撑在软黏土和砂土之上,对应考虑为摩擦桩和端承桩,地表大面积堆载为150 kPa,砂土和黏土的物理力学参数与前述取值相同。 图6 桩身下拉荷载实测结果与计算结果对比曲线Fig.6 Comparison curve between measured results and calculated results of pile's dragload 如图7所示为不同排水条件下端承桩在固结过程中桩身下拉荷载分布随时间变化曲线。由图7可见:对于端承桩而言,固结时间越久,桩身下拉荷载越大;经历相同时间土体固结后,土体排水条件为双面排水时桩身下拉荷载最大值为单面排水的1.4~6.8 倍,最大下拉荷载比值随着固结时间发展逐渐减小。这主要是因为桩身受到负摩阻力作用,端承桩的下拉荷载最大值一般位于深层位置,而单面排水条件下深层土体的变形很小,双面排水则相反,这导致了双面排水时桩土相对位移更大,在相同的侧向刚度作用下,双面排水桩的下拉荷载远大于单面排水桩的下拉荷载。 如图8所示为不同排水条件下摩擦桩在固结过程中桩身下拉荷载分布随时间变化曲线。由图8可见:对于摩擦桩来说,固结时间越久,桩身下拉荷载越大;经历相同时间土体固结后,双面排水时桩身下拉荷载最大值为单面排水的1.4~5.9 倍,比值随着固结时间发展逐渐减小。 如图9所示为不同排水条件下摩擦桩和端承桩的中性面位置随固结的变化曲线,对于端承桩而言,当排水条件为单面排水时,桩的中性面深度随着固结的发展由0.24L(L为桩长)向0.97L移动。单面排水时深层土体的初始沉降变形较小,随着固结过程发展,位移逐渐增大,中性面位置随着桩土相对位移的增大向下移动;对于双面排水条件,桩基中性面稳定在桩尖0.97L附近。 对于摩擦桩而言,单面排水时桩的中性面位置随着固结过程由浅向深移动,最后稳定在0.78L处。对于双面排水条件,摩擦桩的中性面深度随着固结由0.94L向上移动至0.78L。单面排水和双面排水时摩擦桩的中性面移动过程呈现相反趋势,但最终趋近于相同深度。 图7 不同排水条件下端承桩身下拉荷载分布曲线Fig.7 End-bearing pile's dragload distribution under different drainage conditions 图8 不同排水条件下摩擦桩下拉荷载分布曲线Fig.8 Floating pile's dragload distribution under different drainage conditions 图9 不同排水条件下中性面深度变化曲线Fig.9 Neutral plane depth variation curve under different drainage conditions6 1)本文所建立的桩基下拉荷载和中性面位置随固结时间变化的计算方法,可以考虑土体按照非达西流动定律固结沉降的非线性特性,土体沉降、桩身下拉荷载分布曲线与试验结果非常接近,说明本文方法合理可行。 2)固结过程中土体有效应力增加来自于超孔隙水压力的消散,与非达西流动计算结果相比,按照达西流动获得的有效应力过大,高估了桩土界面强度随固结历时的增长速率。 3)单面排水时,摩擦桩和端承桩的中性面位置随固结由上向下移动;双面排水时,摩擦桩中性面位置随固结时间由下向上移动,端承桩中性面则稳定在桩尖附近。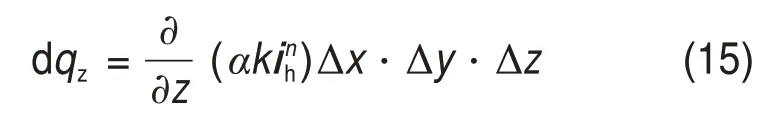


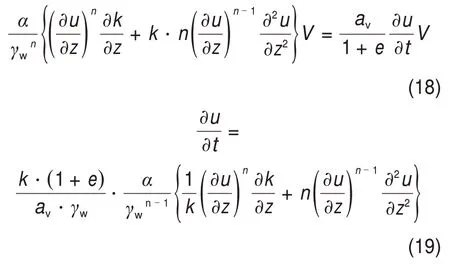
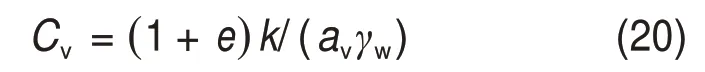
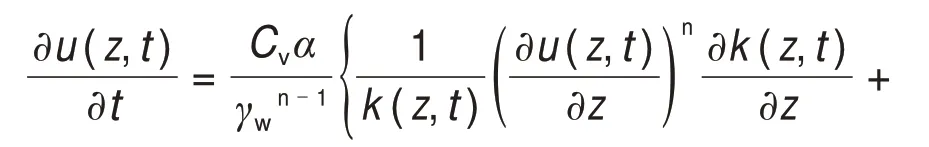
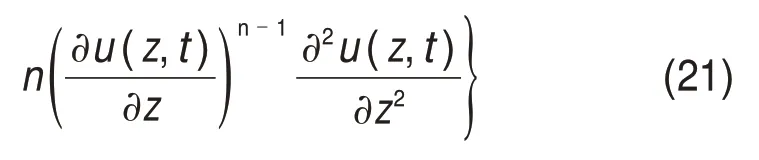
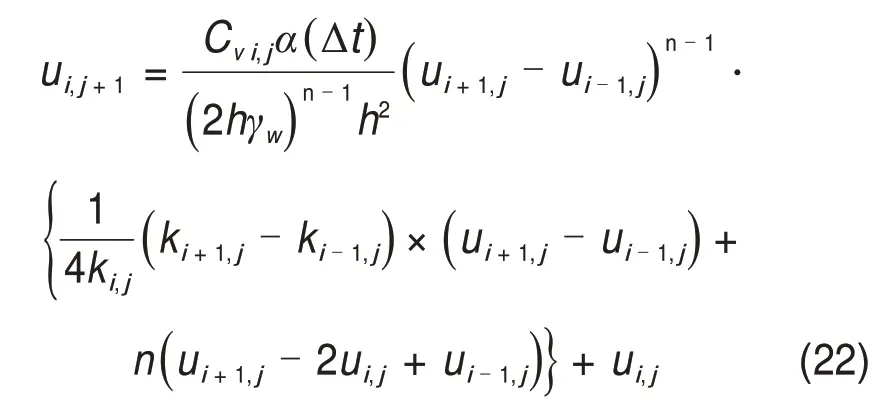

2.2 边界条件与解的稳定性

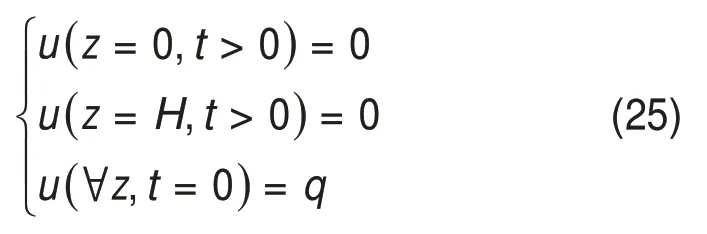
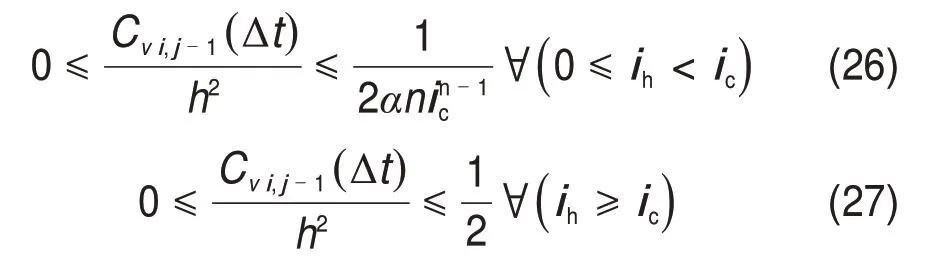
2.3 土体有效应力与固结沉降


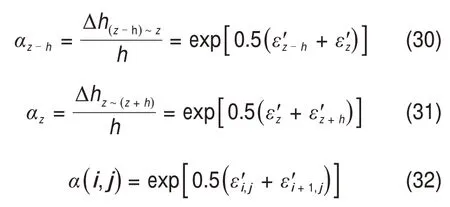
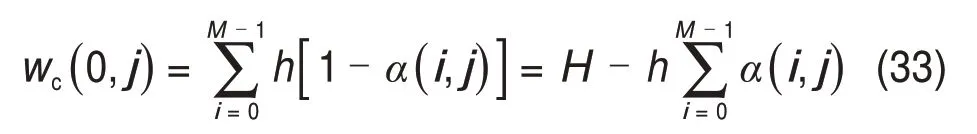
3 荷载传递模型
3.1 桩身轴力位移平衡方程
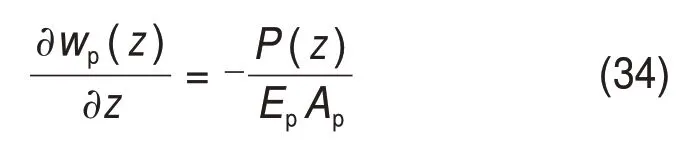
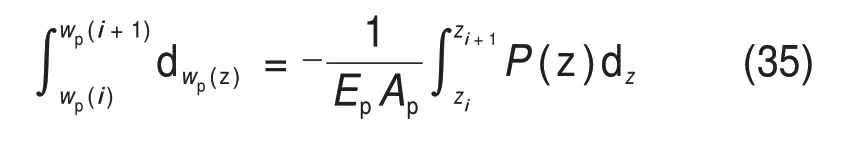
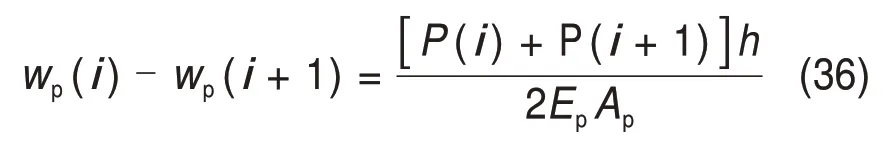
3.2 桩侧摩阻力平衡方程
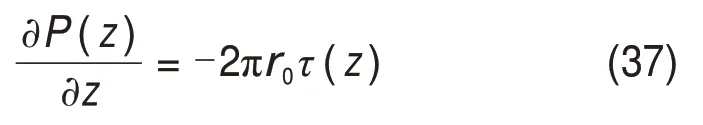
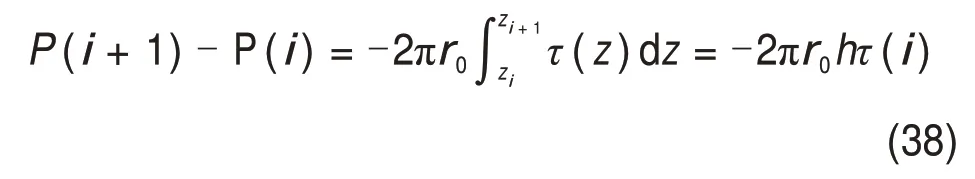
3.3 桩端边界条件
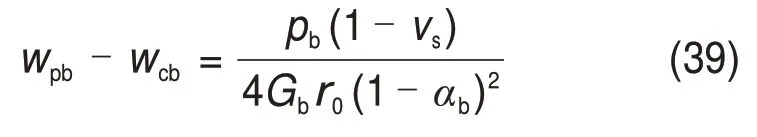
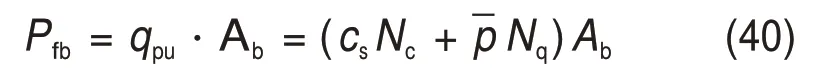
4 案例验证
4.1 试验参数
4.2 计算结果分析

4.3 固结过程中摩擦桩与端承桩下拉荷载变化
4.4 排水条件对桩身下拉荷载分布及中性面位置的影响

5 结论
