疏勒河流域水资源安全评价研究

武兰珍，孙栋元，赵 霞，鄢继选，牛最荣，齐广平

(甘肃农业大学水利水电工程学院，兰州 730070)

水资源是生态环境的重要控制性要素，是基础性的自然资源和战略性的经济资源，也是国家综合国力的有机组成部分[1]。我国水资源短缺，人均水资源占有量仅为世界水平的1/4，水资源时空分布不均匀，尤其是在西北内陆生态环境相对脆弱的干旱与半干旱地区，水资源问题已成为制约当地经济、社会发展的最主要因素[2]。在日益严峻的水资源问题中水资源安全问题日渐突显，水资源安全与否已成为人类生存和发展的保障性基本条件。水资源安全问题成为学界和政府关注的重要议题[3,4]。而水资源安全评价作为水资源安全研究的关键问题之一，越来越受到人们重视。

近年来，国内外众多学者用各类评价指标和各种评价模型对不同区域水资源安全进行了评价。在评价指标的选择中，有单向指标也有综合指标。通常选择区域人均水资源量和水资源开发利用程度作为单项指标[5,6]。但水资源安全作为一个综合性概念，单项指标难以反映水资源安全评价的全部内容，而且这2个单项指标在应用过程中所反映出的水资源安全状况在部分地区可能完全相反，因此构建水资源安全评价综合指标十分必要。国内外常用的水资源安全评价的综合指标有水安全指数( Water Security Index)[7]、水贫乏指数( Water Poverty Index)[8,9]、水压力综合指数( Integrated Water Stress Index)[10]、水短缺指数( Water Scarcity or Shortage Index)[11]、水资源承载力指数( Water Resources Carrying Capacity Index)[12]等，这些指标较为综合地考虑了社会、经济、资源、环境等各方面因素，较为全面地反映出不同区域的水资源安全状况，但这些综合指标数据的可获得性较难保障。在水资源安全评价方法方面，陆建忠等利用综合指数法对鄱阳湖流域水资源安全进行了评价研究[13]；黄乾等建立了基于熵权的水安全模糊物元模型，并对2005年山东省水安全进行了评价[14]；卢敏等用集对分析理论提出了基于集对分析的水安全评价方法[15]；宋培争等运用基于粒子群算法优化的Logistic指数公式对区域水资源安全进行了评价[16]。这些评价模型和方法各有优缺点，基本上都需要根据决策者的偏好和指标体系的特点进行选择[17]。为此，本文提出了一种基于时间尺度具有数据可获得性、结果可比较性的水资源安全评价方法来全面反映以时间为尺度的流域水资源相对安全状况。文章采用AHP(层次分析)和多目标多层次的模糊综合评判模型，选取疏勒河流域为研究区域，结合流域2005-2017年流域内自然、经济、社会和水资源状况等统计资料，对流域水资源安全进行综合评价，以期为区域水资源安全状况做出准确判断，从而为疏勒河流域生态治理和水资源开发利用提供决策依据[18]。

1 研究区概况

疏勒河是地处甘肃河西走廊最西端的3大内陆河之一[2]，干流全长670 m，流域面积4.13 万km2，由于地处西北内陆干旱半干旱地带，流域内多年平均降水量仅为47～63 mm，而年均蒸发量为2 897～3 042 mm，根据2005-2017年《甘肃省水资源公报》中数据显示，流域多年平均水资源总量为25.73 亿m3，用水量为18.4 亿m3。2017年，流域内总人口为53.23 万人，其中城镇人口32.11 万人，农村人口21.12 万人，国内生产总值342.62 亿元，人均GDP为6.44 万元。早在汉唐时期，疏勒河流域就是丝绸之路上的重要产粮区，推动着丝绸之路的发展。目前，流域下辖干流中游昌马灌区、干流下游双塔灌区及花海灌区3大灌区，灌区有效灌溉面积为8.96 万hm2[19]。

2 疏勒河流域水资源安全评价模型

2.1 评价指标体系的确定

水资源安全评价内容丰富，评价对象除水资源本身之外，还包括与水资源相关的众多自然因素、社会经济因素和人文因素等。水资源安全是所有与其相关的多种因素组成的综合水环境系统的安全。因此水资源安全评价所建立的指标体系须全面、完整、准确地反映水资源安全属性。在遵循科学性、典型性、可表征性、可获得性等的原则基础上，借鉴国内水安全评价中的指标体系，结合疏勒河流域实际情况，选取能综合反映疏勒河流域水资源安全状况的20个评价指标，建立由目标层(A)、准则层(B)、指标层(C)3个层次组成的疏勒河流域水资源安全综合评价指标体系。指标的计算公式和选取意义见表1。

2.2 评价指标权重的确定

层次分析法(AHP)是将要进行的决策问题置于一个具有多种因素相互作用的大系统中，并将这些问题层次化，形成多层次结构分析模型，通过两两相比的方法将各不同层次的因素进行判别，确定各因素之间的相对重要程度。疏勒河流域水资源安全即为一个多层次多目标的系统，通过指标分类比较，最终得到影响疏勒河水资源安全的各因素的重要性权值。其具体步骤为:

(1)建立层次结构。根据疏勒河流域具体情况，选取水资源量、供水安全、社会安全、经济安全和生态安全5个层面为准则层，每个准则层又包含若干评价指标[20]，建立流域水资源安全层次结构体系。见表1。

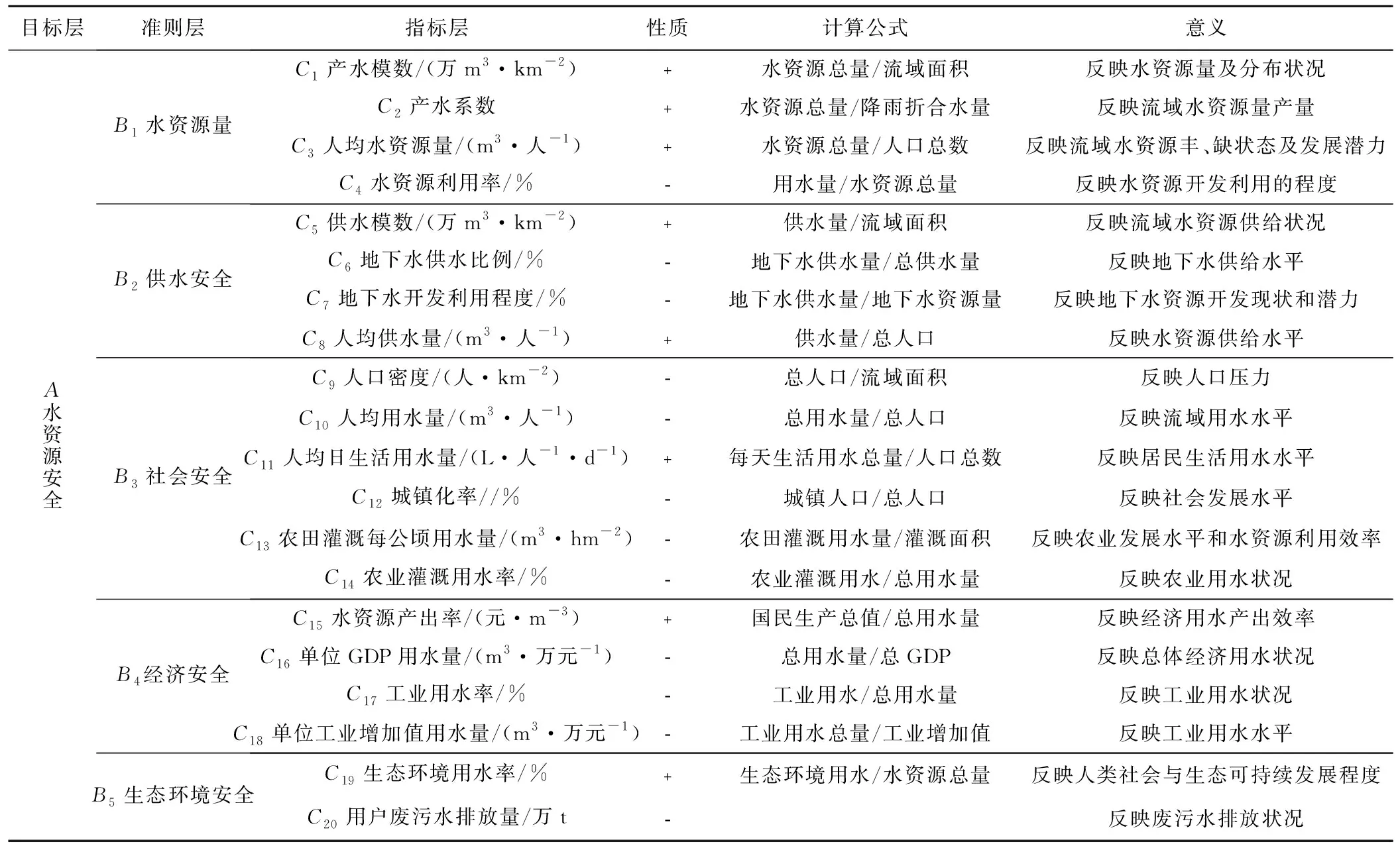
表1 疏勒河流域水资源安全综合评价指标体系Tab.1 Comprehensive evaluation index system of water resources security in Shule River basin

(2)构造矩阵。比较下层因素Ci、Cj(i，j=1，2，…，n)对上层因素Bk的影响。每次取2个因素Ci和Cj，用cij表示Ci对Cj的相对重要度赋值。构成B-C的判断矩阵A：

(1)

(3)权重计算。得到判断矩阵A后，求解判断矩阵A的最大特征根λmax及所对应的特征向量w，将w归一化后，即为各指标因素C1，C2，…，Cn的排序权重。为判断得到的权重是否在合理的允许范围内，需对判断矩阵A进行一致性检验。检验公式为：

(2)

式中：CR为判断矩阵的随机一致性比率；RI为判断矩阵的平均随机一致性指标；CI为判断矩阵一致性指标：

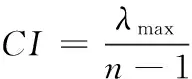
(3)

1～9 阶的判断矩阵的RI值见表2。

表2 平均随机一致性指标RI的取值Tab.2 Mean random consistency index RI

当CR<0.1或λmax=n，CI=0时，判断矩阵具有满意的一致性。否则，应对判断矩阵加以调整。

综上，层次分析法将定性分析与定量判断相结合，较为科学地对各指标进行权重赋值，能够适用于疏勒河流域水资源安全综合评价中各指标的权重赋值。疏勒河流域各评价指标权重和CR值见表3。

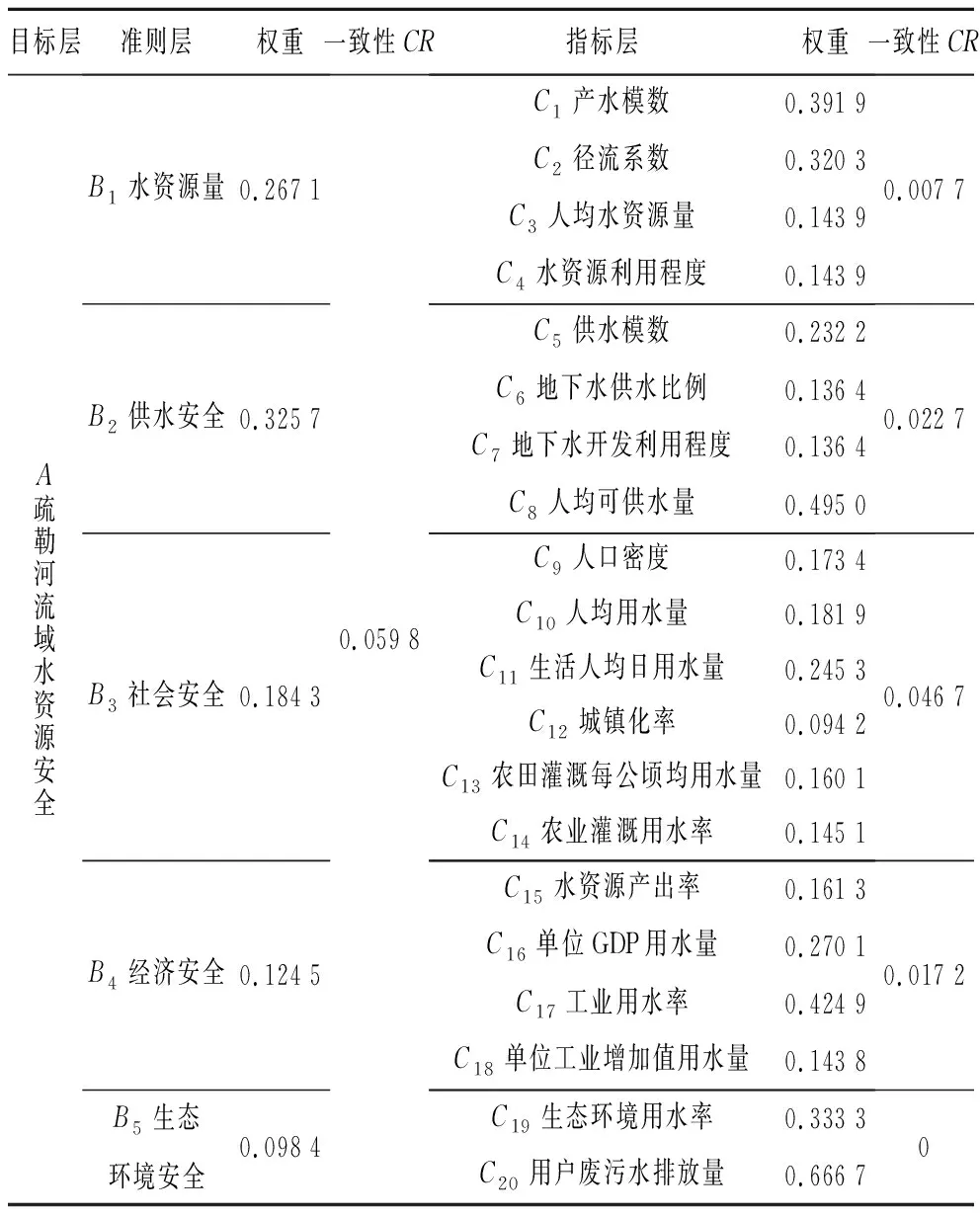
表3 评判指标权重值及一致性检验Tab.3 Weight value and consistency test for each evaluation index

2.3 多层次多目标模糊综合评判模型

多层次多目标模糊综合评价模型以模糊数学为基础，主要针对决策问题中的复杂多目标问题。实际问题往往需要评价复杂系统，因此按照一定规则对评价内容逐级进行分类归纳，构成不同方案，评价每个方案内容，将得出的结果再次作为评价内容，不断重复，最终得到最高层次的唯一值作为评价优属度状况。

2.3.1 多层次多目标模糊评价模型的建立与运算

(1)确定目标集与方案集。设某一决策方案的结构形式为Mj(j=1,2,…,n)，则M=(M1,M2,M3,…,Mn)表示依照顺序通过排列集合得到的方案集。以不同层次等级对目标集进行分层，不同对应方案下所影响的不同目标的结构形式用gi(i=1,2,…,m)表示，则能够得到m个独立目标构成的目标集G={Z1,Z2,…,Zm}，若用t个评价体系对目标集G进行归类，将得到t个不同的类别，即G={G1,G2,…,Gt}。进行归类后的目标集中的每一个子集仍就以不同的目标值组成，得到G={g1k,g2k,…,gmk}(k=1,2,…,t)。进行细分后，将第1次所划分形成的G={G1,G2,…,Gt}看作目标集的首层，以此类推，将第2次划分的目标Gk={g1k,g2k,…,gmk}(k=1,2,…,t)作为目标集的下一层。由于方案集与目标集呈现出两两对应的关系，令xij(i=1,2,…,m,j=1,2,…,n)为方案对目标的属性关系指标量，则可用矩阵Xij=(xij)m×n表示m个目标对n个决策方案关于目标特征值的矩阵[21]：

(4)

(2)计算指标相对隶属度。目标界定过程中，指标可分为成本型和效益型2类。

成本项指标：目标特征值越小越优秀的指标，隶属度构造公式为：

效益型指标：目标特征值越大越优秀的指标，隶属度构造公式为：

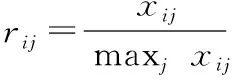
式中：rij表示方案对目标的相对隶属度；xij是方案目标的特征值。

综上，每一个目标对应的隶属度所构成的矩阵为R：

(5)

疏勒河流域水资源安全评价各指标隶属度表4。

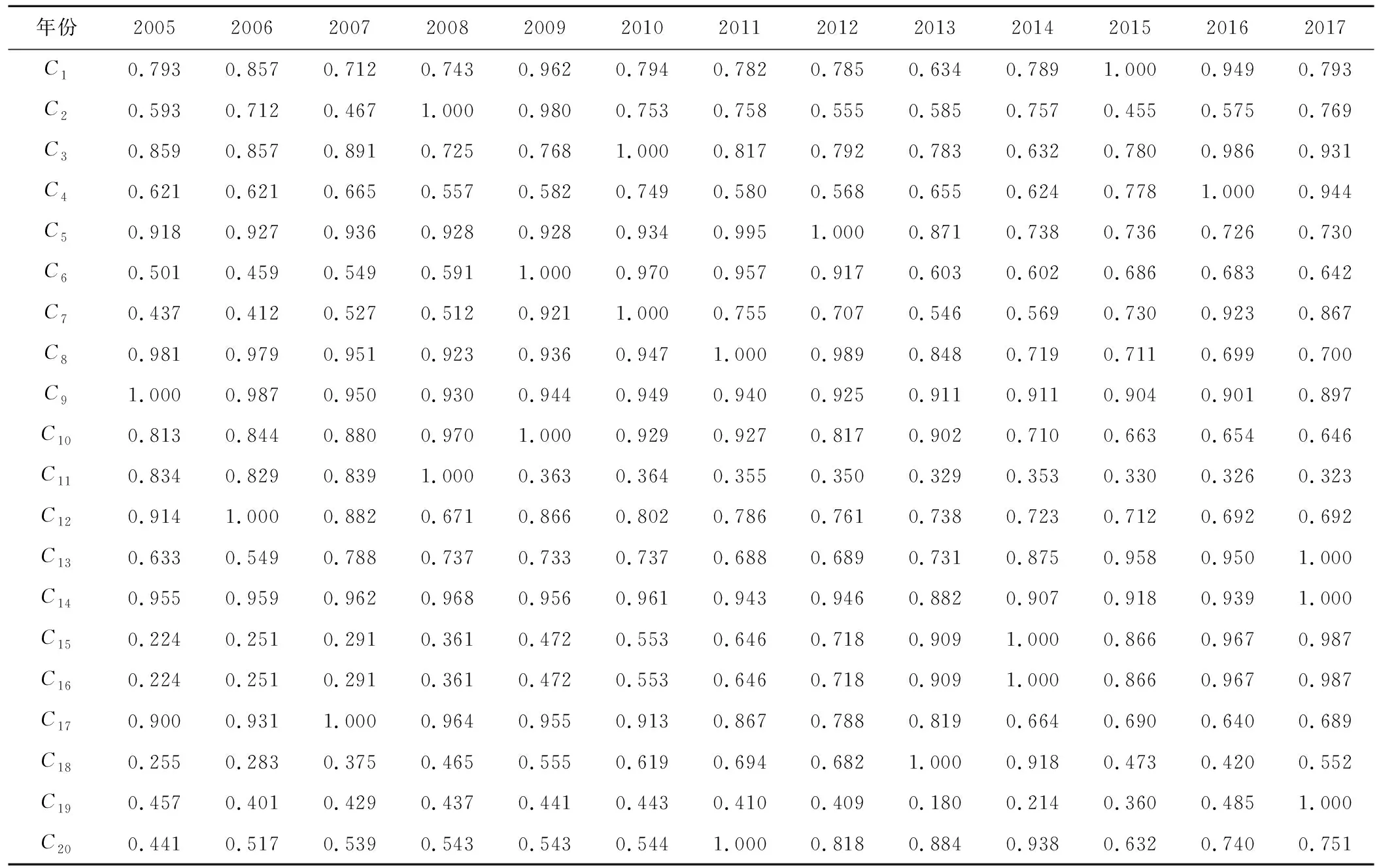
表4 疏勒河流域水资源安全评价各指标隶属度Tab.4 Subordination degree of water resources security assessment indexes in Shule River basin

(3)构建评价体系中的最优及最劣方案。对于方案集中不受其他平行方案影响的评价方案，建立最优方案与最劣方案。即抽出矩阵R中的每一行的最大值：

rg=(rg1,rg2,…,rgn)=

(maxr1j,maxr2j,…,maxrmj)=(1,1,…,1)

(6)

为理想优等方案。

同理抽出矩阵R中每一行的最小值：

rb=(rb1,rb2,…,rbn)=

(minr1j, minr2j,…,minrmj)=(0,0,…,0)

(7)

为理想的劣等方案。

任何一个方案Mj都将以优属度ugi、劣属度ubj隶属于优等方案rg和劣等方案rb。由此模糊划分矩阵U被建立：

(8)

式中：0≤uji≤1,0≤ubj≤1,uji+ubj=1,j=1,2,…,n)。

(4)模糊优选模型的建立。利用上述层次分析法得到各指标权重的加权向量，建立方案Mj与最优等方案相对应的隶属度ugi的最优值的优化准则，即：

(9)

(10)

式(9)为多目标模糊优选模型，其中ugi为决策优属度。

最后，建立每个决策系统当中m个子系统的模糊关系矩阵irgi，将m个矩阵中所对应的不同元素依次合成，就可得到如下的多目标模糊矩阵U：

所以，如果各子系统的加权向量w=(w1,w2,…,wm)能够计算出n个系统方案的决策优属度，以此类推，则将计算求得的底层指标决策优属度确定为每个单元更高一层的评价指标，然后再进行计算，这样从最低层逐层向上一层进行模糊优化运算。当最高一层只剩唯一一个单元时，则能够求出最高级的单元系统也是整体方案的优属度向量：

uj=(u1,u2,…,un)

(12)

多层次多目标模糊综合评价模型是从每个准则层的各个指标开始计算，用每个指标的权重进行赋值，然后再利用多层次多目标模糊综合评价模型求出决策优属度向量，用求得的决策优属度向量逐层计算更高一层的决策优属度，求得最高级的决策优属度向量。值得一提的是，此方法评价的结果并不能代表系统的绝对优劣程度，而是相对的判断。优属度表示该指标相对于优秀状态的程度，优属度越高，情况越优秀。

2.3.2 多层次多目标模糊综合评价模型在疏勒河流域水资源安全评价中的应用

以时间尺度为基准对疏勒河流域水资源安全进行评价，选取2005-2017年疏勒河流域水资源安全评价指标，采用多层次多目标模糊综合评价模型，对疏勒河流域13 a的水资源安全状况进行综合评价。以疏勒河流域13 a中每一个不同年份为方案集，即M=(M1，M2，…，M13)。根据疏勒河流域水资源安全综合评价指标体系，从最底层开始经过逐层计算，最后得到最高层次决策优属度向量即水资源安全优属度。计算出的优属度值越大，表示水资源安全状况相对越安全。疏勒河流域水资源安全评价各层次决策优属度见表5和图1。

表5 疏勒河流域水资源安全评价目标层决策优属度Tab.5 Decision-making superiority degree of each target level for water resources security assessment in Shule River basin

图1 疏勒河流域水资源安全评价各准则层决策优属度Fig.1 Decision-making superiority degree of each criterion level for water resources security assessment in Shule River basin

3 疏勒河水资源安全评价结果分析

由于多层次多目标模糊综合评价模型并不是对水资源安全优劣进行绝对评判，而是以时间为尺度，对水资源安全状况进行相对定论，所以本文以年为单位，对疏勒河水资源安全进行相对状况分析研究。根据表4、表5、图1的内容，按照不同层次优属度属性，得出基于时间尺度的2005-2017年13 a的疏勒河水资源安全相对状况。

疏勒河水资源安全状况是一个动态变化过程，其安全度大小通过每一年水资源安全优属度的上下浮动值表示。由于优属度表示其隶属于优的程度，所以优属度越大则水资源安全状况越优，即越安全；反之，优属度越小则水资源安全状况越差。从表5中可以看出，疏勒河13 a中水资源安全情况的排名为2015年<2014年<2005年<2016年<2007年<2017年<2012年<2006年<2013年<2009年<2010年<2008年<2011年。其中2015年优属度最小，表明2015年水资源安全状况相对于其他年份最不乐观；而2011年水资源安全优属度值最大，表明2011年疏勒河流域水资源安全状况相对于其他年份是最好的。表5中数据显示2014年与2015年疏勒河流域水资源优属度较低。究其原因是因为2014年甘肃省实施《最严格水资源管理制度考核办法》，考核办法中明确提出了用水量考核[22,23]，因此疏勒河流域用水量从2012年的20.84 亿m3降低到了2013年的18.14 亿m3，2014年则降至15.38 亿m3，2015年为15.34 亿m3，呈现逐年降低的趋势，直到2017年用水量才略有增加。

从图1准则层优属度状况可看出，准则层优属度变化浮动较大的是B5生态环境安全方面，其中2005年优属度最低，2011年优属度最高，但优属度为整体上升趋势，2011-2015年优属度降低幅度较大，2015年达到最低状态，2015年之后优属度又有上升。主要原因是疏勒河流域用水主要以农业灌溉为主，农业用水占比高达80%左右，根据 2003-2015 年昌马、双塔和花海3大灌区引水量及昌马总干渠引水量统计资料，昌马总干渠的年引水量均超出了省定额水量，且表现为逐年上升的趋势，农业用水严重挤占生态用水。

其次2013年甘肃省开始实施《最严格水资源管理制度考核办法》，为了达到考核目标调整流域用水结构，生态用水被严重挤占，2013年流域生态用水量达到最低值，生态环境用水率仅为1.9% 。因此，恢复流域生态用水是流域后续水资源合理配置的重要工作。2013年之后，由于对沙漠绿洲生态问题的关注，为解决敦煌生态问题，甘肃省实施《敦煌水资源合理利用与生态保护综合规划( 2011-2020 年)》，流域生态用水量在2013年后有所增加，2014年疏勒河流域生态用水率为2.2%，2015年为3.8%，2016年为5.0%，已超过流域2005-2017年13 a平均生态用水率4.5%，2017年提高至10.4%。

准则层中B4为流域经济安全，由图1可看出流域经济安全优属度整体为上升趋势。但在2013年后优属度呈现下降趋势，疏勒河流域原有的矿产资源逐渐枯竭，疏勒河流域工业产值有逐渐下滑的趋势，因此经济安全优属度在2013年后有下降趋势，然而伴随着国家生态屏障示范区的建立，第三产业有逐渐兴起的趋势，因此2017年经济安全优属度又有所升高。准则层中B3为流域社会安全，流域社会安全优属度整体为上升趋势。影响社会安全优属度中与农业用水相关指标权重为0.305 2，但流域内灌溉用水并没有实施明确的作物每公顷配水定额，也未对农户灌溉进行用水限制，仍以大水漫灌为主，农业灌溉的节水意识不强[24]。如果改变现状，由耗水型向节水型转变的同时加强流域水资源管理，流域社会安全优属度仍有一定提高空间。B2为流域供水安全，呈现出整体恶化趋势。因此，提高流域供水安全也是流域未来在水资源规划和配置应重点关注的主要方向之一。B1为流域水资源量，从图1中可以看出 2010年和2017年流域水资源量优属度2次出现峰值，水资源量优属度最低值出现在 2014年，该变化规律和流域水资源变化状态基本吻合，流域水资源总量2010年和2016年出现峰值，2014年流域水资源总量出现最小值为 13.03 亿m3。

4 结论与讨论

通过AHP和多目标多层次模糊综合评价模型对2005-2017年疏勒河流域水资源安全进行综合评价，研究结果表明：

(1)在2005-2017年中疏勒河流域水资源安全状况最好的为2011年，水资源安全状况最差的为2015年。其中供水安全在水资源安全中所占比重最大，权重为0.325 7；生态环境安全在水资源安全中所占比例最小，权重为0.098 4。

(2)AHP和以时间为尺度的多层次多目标模糊综合评判模型，可相对评价出历年疏勒河流域水资源安全状况的变化情况，具有较强的可行性。其中AHP能够较好地确定权重，它把影响疏勒河流域水资源安全的各因素划分成相关联、条理化的有序层次，并根据专家打分和数学计算得出合理权重。利用AHP得到的各评判因素的权重，通过多目标多层次模糊综合评判模型建立疏勒河流域综合模糊评判矩阵并对其安全状况作出多因素综合评价，得出基于时间尺度的长序列疏勒河流域水资源安全相对状况，反映历年水资源安全的变化情况，为疏勒河流域今后的生态恢复、水资源合理开发利用以及社会经济的可持续发展提供决策依据。

(3)国家政策调控和流域自身用水结构是否合理是目前影响疏勒河流域水资源安全的重要因素。因此，在继续调整经济结构转变增长方式同时，提高水资源的利用效率，出台合理的水资源管理体制，合理规划用水结构是疏勒河流域水资源安全的根本保障。

此外，本文虽提出了一种既能较为全面反映水资源安全状况，又基于时间尺度上具有数据可获得性、结果可比性的水资源安全评价方法，但仍有不足之处：一方面国内外对水资源安全没有统一认识及数据资料限制，指标体系的设计还有待完善，如生态环境指标中由于数据难以获取，仅考虑了生态环境用水率和用户污水排放量2个指标；另一方面AHP法虽然确定了指标权重，但权重确定过程中的专家打分环节存在专家的主观意识，并不能完全客观地反应指标之间的相对重要程度；其次，通过多目标多层次模糊综合评判模型计算出的结果，并不是对水资源安全优劣进行的绝对评判，而是以时间为尺度，对水资源安全状况进行的相对定论。