基于英飞凌TC275的火箭智能稳定控制演示平台设计

罗轶欣，王俊鸿，闻 新，龙弟之

（南京航空航天大学 航天学院，江苏 南京 210016）

自动控制技术被广泛应用于航天领域，如卫星的轨道及姿态控制、运载火箭的姿态控制等。而“航天器控制技术与应用”则是专门针对航天类专业开设的控制课程，其中运载火箭姿态控制原理内容比较抽象，控制对象比较复杂，属于非线性问题。在实验教学过程中，运载火箭控制过程通常会采用计算机进行模拟仿真演示，只能根据过程状态量的变化曲线进行讲解与分析。对于初次接触航天专业知识的学生来说，仿真实验过于理论化，可操作性和可视化程度不高，不利于培养他们的独立思考精神和学习兴趣。

在航天工程中，运载火箭垂直上升段属于加速段，涉及俯仰、滚转和偏航三通道的姿态控制[1-2]，其中俯仰角的控制可以抽象成传统倒立摆的稳定控制[3-5]。基于此，为了让学生对运载火箭垂直上升段姿态变化和控制过程有更直观的了解，本文在机械结构创新的基础上，结合运载火箭姿态控制原理及智能控制算法，以英飞凌TC275为控制芯片设计了火箭加速上升段稳定控制演示平台，并利用 MATLAB对控制算法进行仿真和验证测试。该演示平台应用于实验教学中，能够加深学生对航天控制系统理论知识的理解，提高学生的动手创新能力，达到理论与实践相结合的教学要求。

1 基本设计思路

综合考虑平台的稳定性以及各部件的尺寸大小、安装位置，用Solidworks软件对火箭智能稳定控制演示平台的机械结构进行设计，3-D模型如图1所示。

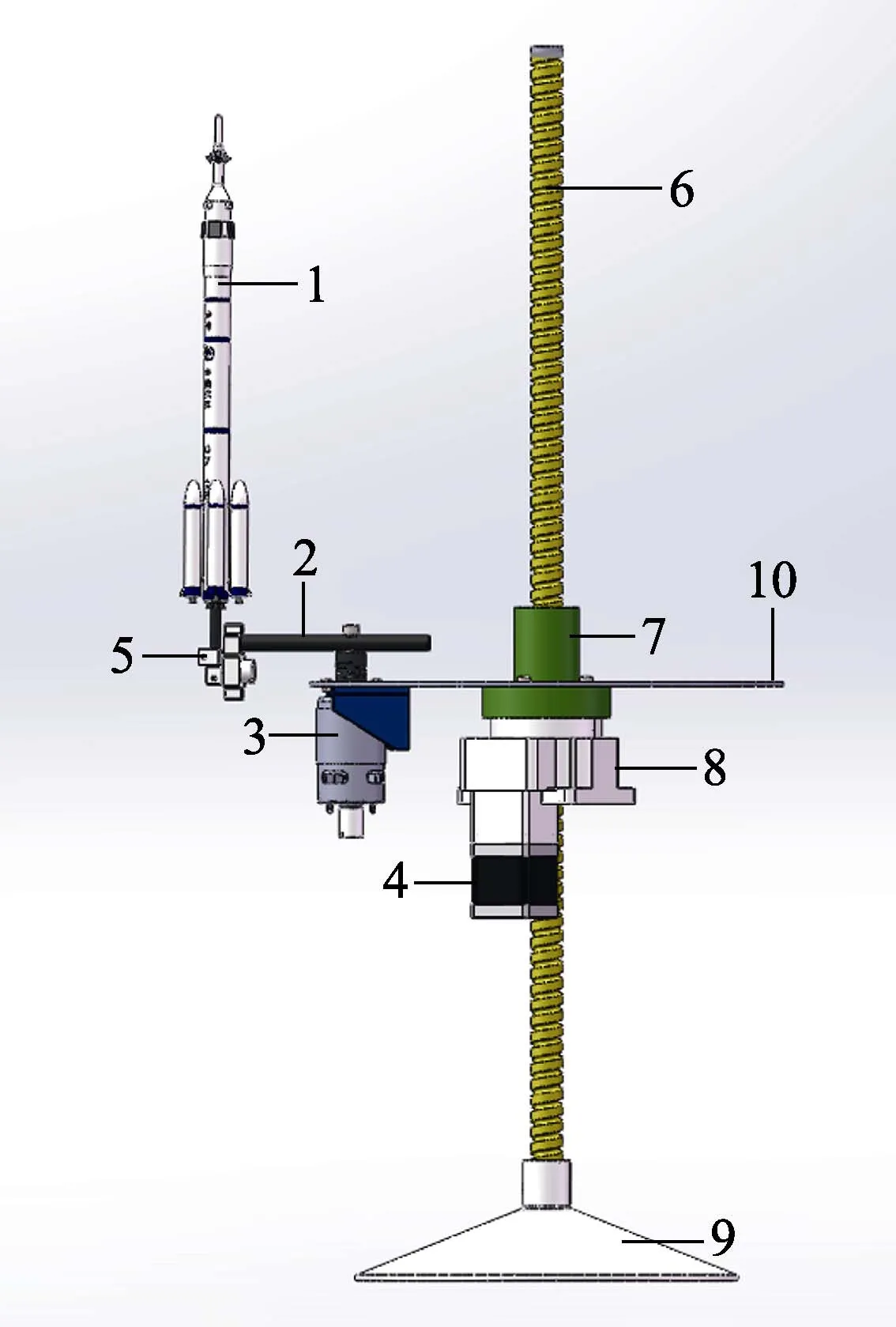
图1 平台3-D模型

平台控制器采用的是英飞凌TC275多核芯片，该芯片包含3个200 MHz、32位的CPU内核（CPU0、CPU1、CPU2），它们共享总线资源，分别拥有自己独立的RAM，每个内核都可以访问任何外设。该芯片支持I2C、SPI以及UART通信，拥有12个模数转换器（ADC）、12个PWM通道、3个内部时钟。该芯片足以满足平台工作需求。平台控制部分设计充分利用芯片多核优势，将控制任务分为两部分：CPU0控制抬升装置，实现平台加速上升；CPU1则实现火箭模型的稳定控制。当系统启动时， CPU0驱动步进电机带动中空电机减速箱，使控制平台在丝杠上做加速上升运动。角度传感器和直流电机编码器分别测得火箭模型的俯仰角1θ和转臂的转动角度2θ，测得的数据通过ADC通道传入CPU1，通过相应的控制算法计算控制量，并利用驱动模块控制直流电机加速或减速来实现火箭模型俯仰角和转臂转动角度稳定在期望值。平台总体设计框图如图2所示。

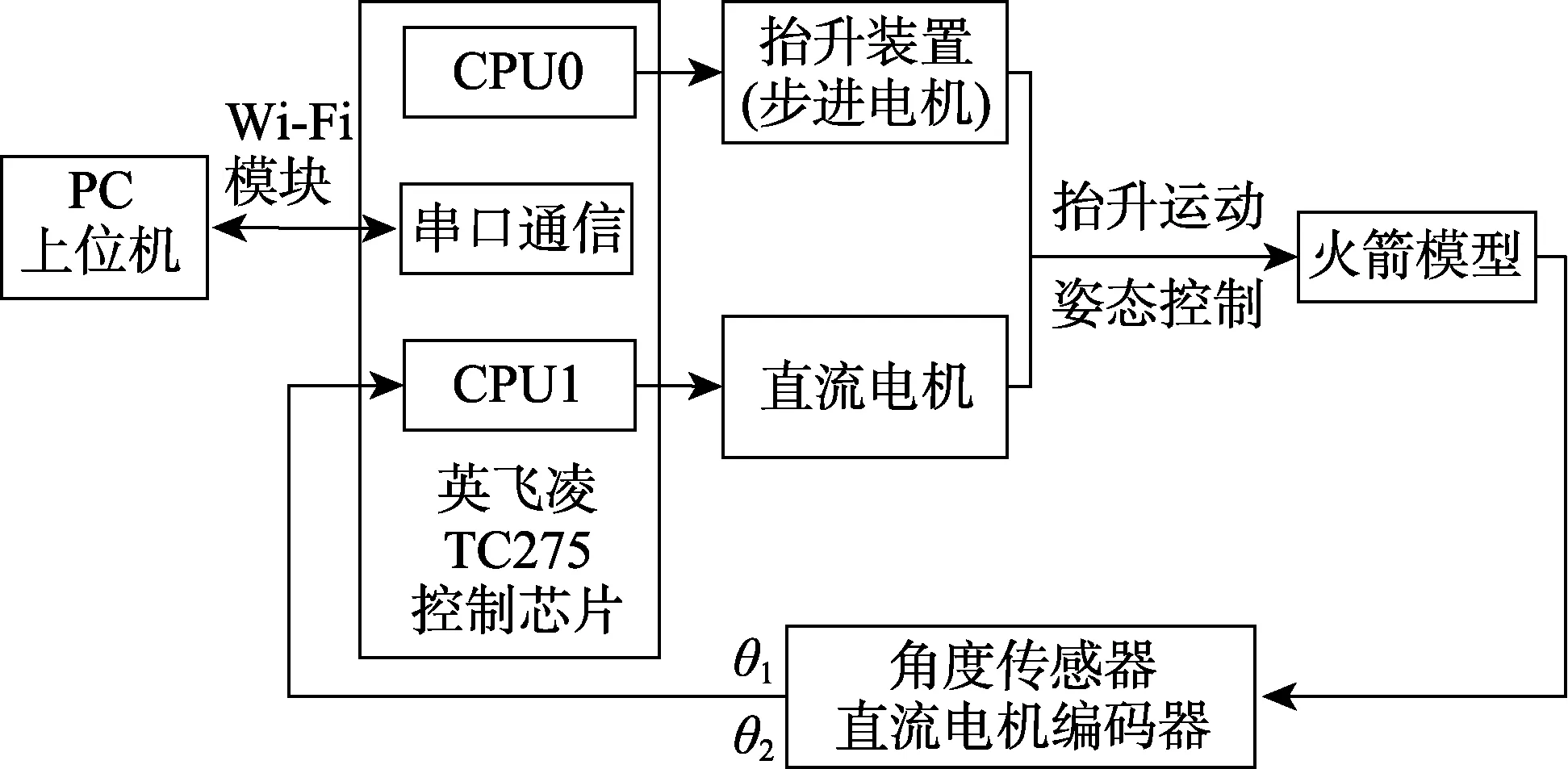
图2 平台总体设计框图

2 模型建立

由于控制平台是加速上升的，数学模型建立在传统的旋转倒立摆数学模型基础上，引入了一个平台竖直向上的位移量z0。选用欧拉-拉格朗日法对平台数学模型进行分析[6-7]，建立如图3所示的坐标系。

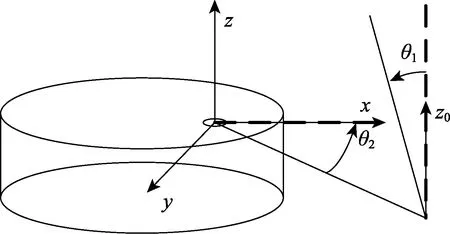
图3 平台建模分析简图

转臂的动能、势能分别为：

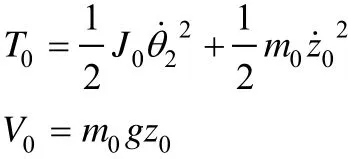
火箭模型在坐标系中存在如下关系：

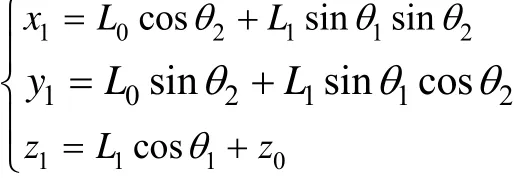
火箭模型的动能、势能分别为：

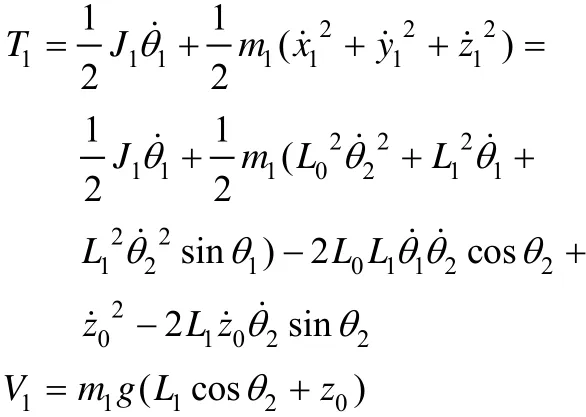
根据拉格朗日方程：

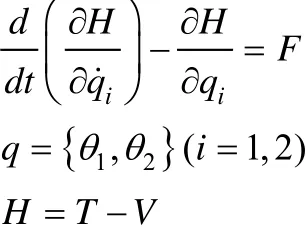
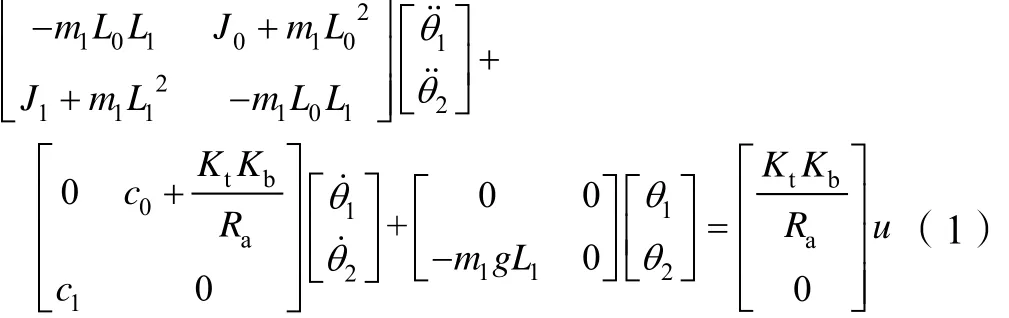
系统中物理量的实际值如表1所示。

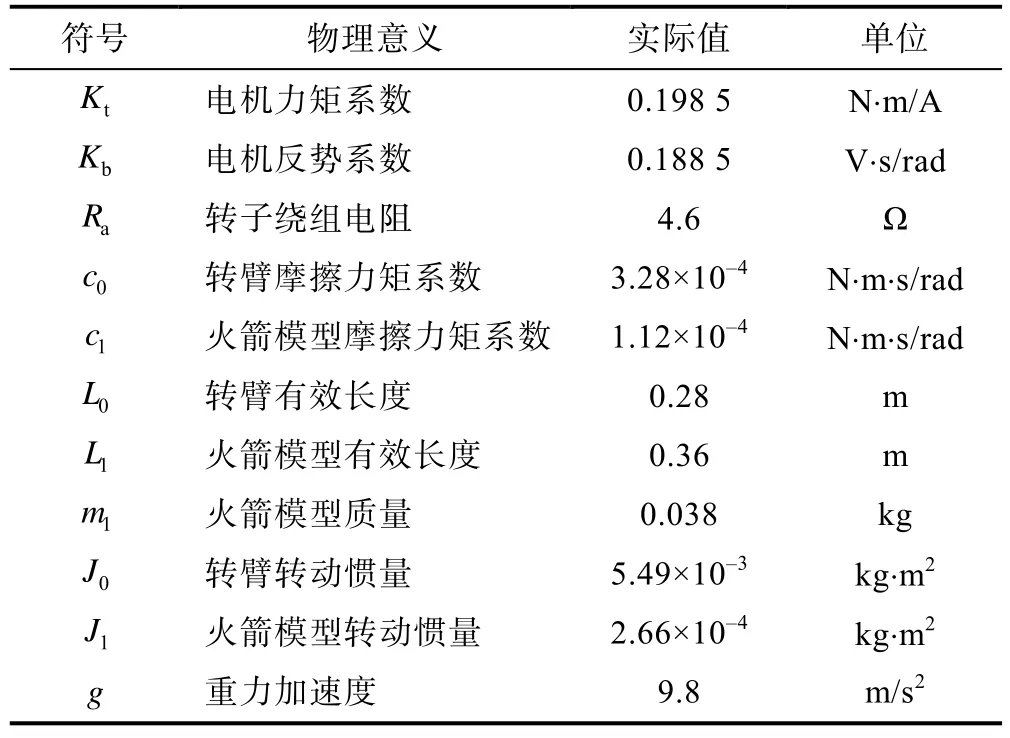
表1 系统物理量实际值

将各物理量代入方程（1）中，得到系统状态空间表达式为

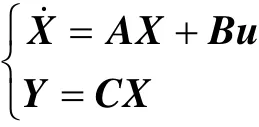
其中：

3 控制器设计与仿真

3.1 PID控制算法

PID是目前应用最广泛的工业控制器，如今运载火箭的姿态控制方法仍以传统的PID控制算法为主。本平台运用模型角度环和转臂角度环的双闭环PID控制算法实现对火箭模型的俯仰角的控制[8-9]。由于转臂的转动偏差对于火箭模型的俯仰角控制是一种干扰，因此两个控制环的输出要进行错频处理。在MATLAB平台上进行Simulink仿真，验证控制器的稳定性，设计控制律为

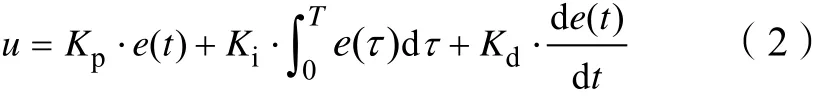
根据式（2），设该控制器的6个控制参数分别为Kp1、Kd1、Ki1、Kp2、Kd2、Ki2，PID 控制器的输入分别为模型角度偏差量e1、转臂角度偏差量e2。通过调试得到，模型角度环 PID参数为Kp1=300、Kd1=24、Ki1=110，转臂角度环 PID 参数为Kp2=8、Kd2=13、Ki2=0.02时，控制性能最优。

3.2 BP神经网络控制器

传统的PID控制器在运行之前需要进行参数的整定，面对新的被控对象或者模型结构改变，原先整定好的参数无法实现较好的控制。BP神经网络控制器作为一种智能控制器，具有较好的自适应学习能力和较强的鲁棒性[10]。在不需要被控对象的准确数学模型情况下，BP神经网络控制器通过数据集进行离线训练，利用学习算法对网络内部参数不断进行修正，最终实现系统的稳定控制，为非线性系统建模和控制提供了有力的工具。

本节在节3.1的基础上，用BP神经网络控制器替代PID控制器，实现对火箭模型的稳定控制[11]。让学生通过仿真和实验操作，深入了解智能控制器，达到更好的教学效果。

首先，利用节3.1的仿真模型采集e1、e2和控制量u的数据集，共采集140 000组数据。对这些数据进行归一化处理，以提高神经网络控制器的收敛速度和控制精度。

然后，搭建 BP神经网络控制器仿真模型。本文利用 MATLAB实现神经网络的初始化和训练[12]。设置输入层、隐藏层及输出层节点为[2 15 1]，激活函数为purelin，为避免陷入局部极小值，选用Levenberg-Marquardt作为训练算法。

训练中，设置学习率为0.01，并选取两个终止准则：迭代达到1 000次和最小训练误差小于0.001。利用处理后的数据集完成训练后，通过gensim函数生成神经网络控制器模块，并在Simulink中搭建仿真模型，如图4所示。

3.3 仿真与分析

将上述两种控制器运用在相同初始条件的被控系统中，对仿真结果进行比较。

模型偏角、转臂偏角、模型角速度以及转臂角速度的初始条件设置为[1.3 rad, 0 rad, 0 rad/s, 0 rad/s]，两种控制器下的系统响应曲线如图5所示。

从图5(a)可以看出：使用PID控制器，火箭模型角度最大超调量为-0.54 rad（约为-31.33°），系统最终稳定时间约为1.46 s；使用BP神经网络控制器，火箭模型角度最大超调量为-0.56 rad（约为-32.41°），系统最终稳定时间约为1.3 s；PID控制器总体上符合系统控制要求。

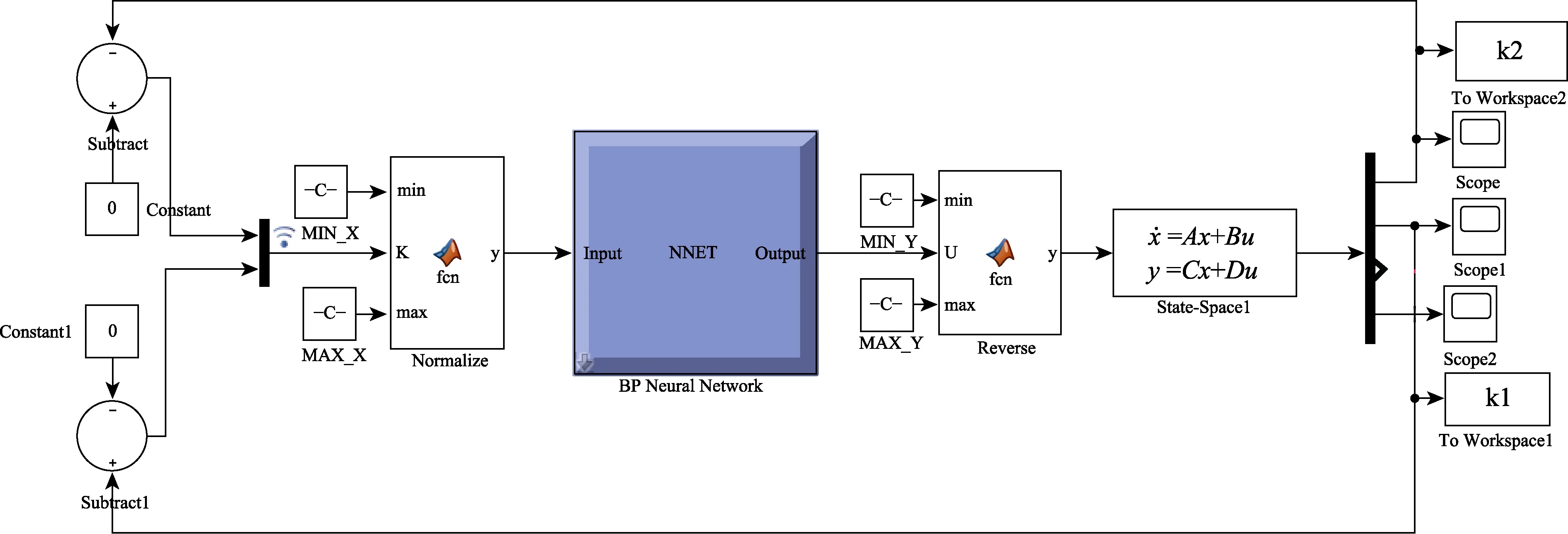
图4 BP神经网络控制器仿真图

图5 两种控制仿真效果图

从图5(b)可以看出：使用PID控制器，转臂角度最大超调量为0.52 rad（约为29.87°），最终稳定时间约为3.1 s；使用BP神经网络控制器，转臂角度最大超调量为0.53 rad（约为30.22°），最终稳定时间约为

2.18 s。

对比两种控制器的仿真效果图，由于神经网络具有良好的动态特性，其控制效果在逼近PID控制器效果的同时，状态参数的稳定时间明显缩短，优化了传统控制器的性能。

4 实物平台验证

平台实物按照节1的3-D模型图进行搭建，如图6所示。控制系统在 Arduino软件开发环境中编写。平台控制程序总体流程图如图7所示。

图6 演示平台实物

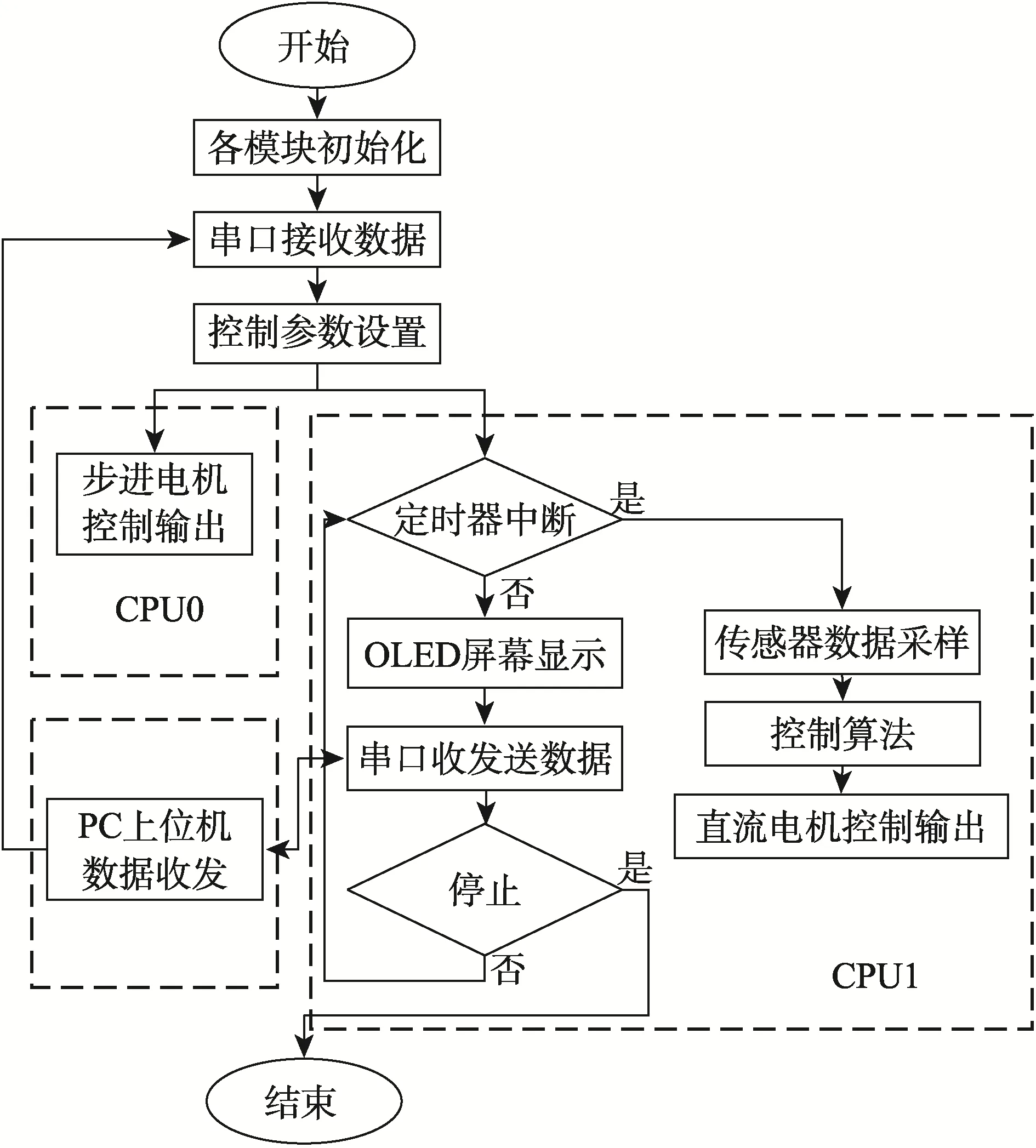
图7 平台控制程序总体流程图

首先对单片机所用到的I/O口、内部中断、串口、ADC数模转换等模块进行初始化，之后通过串口等待接收 PC上位机的调整参数指令以及平台启动指令，并根据指令设置控制参数。在CPU0程序中，主要实现步进电机的驱动控制，并可通过 PC上位机改变平台上升速度；CPU1程序中，进入主程序后，驱动OLED显示，进行串口收发数据，根据flag变量值确定控制算法类型，并确定控制参数。平台每5 ms会进入中断程序，对传感器数据进行采样；每25 ms根据已设定好控制参数的控制算法对模型输出控制量，通过PWM信号驱动直流电机实现稳定控制。最终由 PC上位机关闭平台。两种控制算法根据仿真模型的控制器结构和公式进行编写，控制参数在仿真整定的基础上，根据实物控制效果进行调整，达到最优[13]。

控制系统外接无线 Wi-Fi模块，在 PC上位机上安装与其配对的无线Wi-Fi模块，可通过串口实现数据实时传输，相比传统的数据线传输，无线模块传输可以不受线长的约束，更加灵活便捷；同时可以实现局域网传输，控制系统的数据可以传输到局域网内的PC上位机上，方便课程教学与实验。在PC上位机上，利用MATLAB平台上的GUI软件制作了上位机程序，具备五项功能，分别为串口配置功能、数据收发功能、控制算法选定功能、控制参数设置功能和曲线绘制功能，便于学生进行实验对比与结果分析。

图8和9分别为两种控制器对实物平台的控制效果图。可以看出，与仿真结果类似，两种控制器都能较快使火箭模型稳定在竖直状态并随平台加速上升，很好地验证了控制算法的可行性，达到了设计预期效果。

图8 PID控制器对平台的控制效果

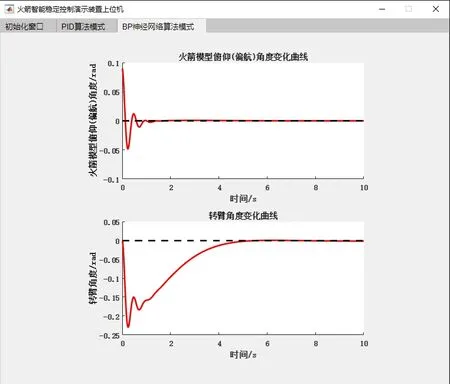
图9 BP神经网络控制器对平台的控制效果

5 结语

本文针对“航天器控制技术与应用”专业控制课程，在传统的倒立摆基础上进行机械结构的改进，搭建了火箭智能稳定控制演示平台，分别运用PID控制算法和 BP神经网络控制算法实现数学模型仿真以及实物控制，同时平台配套设计了 PC上位机程序，实现对演示平台的控制以及实时获取火箭模型状态变化曲线。将该演示平台应用于本科实验教学，能以实物的形式向学生直观地展示运载火箭姿态控制过程，使学生对抽象复杂的火箭姿态控制原理有更深入的理解；同时通过采用不同的控制算法，对比分析传统算法和智能算法的优缺点，满足了理论与实际相结合的课程教学要求，充分调动了学生对课程的学习兴趣，有助于引导学生进行探究实验与创新实践，为培养具备扎实专业技能的创新型人才打下坚实基础。

参考文献 (Reference)

[1] 丰晓霞，夏广庆，韩秀利，等. 运载火箭姿态控制系统稳定性分析[J]. 大连理工大学学报，2015(5): 542-547.

[2] 王晓东. 导弹和运载火箭姿态稳定与控制技术发展的回顾和展望[J]. 导弹与航天运载技术，2003(3): 25-30.

[3] 邓朝结. 基于 2-dof机械臂的平面倒立摆的建模与分析[J].现代企业教育，2009(22): 76-77.

[4] YUAN S Q, ZHANG S S. Inverted pendulum teaching experiment platform based on MATLAB-DSP[C]//Proceedings of 2013 International Conference on Education Technology and Information System (ICETIS 2013). Paris, France: Atlantis Press, 2013: 769-772

[5] 李东，陈强，孙振国，等. 倒立摆教学实验系统的设计与应用[J]. 实验技术与管理，2006(9): 100-102, 106.

[6] LUO Z, ZHAO S X, SHI Z Y, et al. Inverted pendulum system control based on state observer and experimental investigation[J].Journal of Northeastern University, 2010, 31(1): 107-110.

[7] 刘继光，王丽军，袁浩. 自立倒立摆系统的自摆起及稳定控制[J]. 实验技术与管理，2015, 32(11): 62-65, 72.

[8] ATMAJA B K, JOELIANTO E. Surface control design of rocket using MIMO PID robust integral backstepping[C]//2011 2nd International Conference on Instrumentation Control and Automation (ICA 2011). Bandung, Indonesisa: IEEE, 2011:370-377.

[9] DOKUMACI K, AYDEMIR M T, SALAMCI M U. Modeling,PID control and simulation of a rocket launcher system[C]//2014 16th International Power Electronics and Motion Control Conference and Exposition. Antalya, Turkey: IEEE, 2014:1283-1288.

[10] 张秀艳，陶国彬，刘庆强. 基于 Simulink的 BP神经网络实现研究[J]. 佳木斯大学学报（自然科学版），2007(5):587-589.

[11] ZHOU J, ZHOU C S, CHEN X. GA-BP neural network control for ducted rocket gas regulating system [J]. Computer Simulation, 2015, 32(1): 56-59, 201.

[12] 周开利. 神经网络模型及其 MATLAB仿真程序设计[M]. 北京: 清华大学出版社，2005.

[13] 倪天龙. 人工神经网络在 ARM 平台上的应用[J]. 单片机与嵌入式系统应用，2005(5): 15-17, 21.