欠驱动门式起重机控制系统仿真实验

石怀涛，李 刚

（沈阳建筑大学 机械工程学院，辽宁 沈阳 110168）

欠驱动系统是指独立控制量的数量少于系统自由度的系统[1-2]，门式起重机是典型的欠驱动系统。门式起重机结构简单、造价低廉、吊运起重高效、系统灵活，广泛应用于港口、车间、物流中心、建筑工地等诸多生产领域。门式起重机控制系统的主要作用是使负载准确、高效地吊运至目的地，并且抑制吊运过程中负载的摆动[3-5]。为了提高门式起重机的使用效率和安全性能，国内外学者进行了广泛深入的研究。文献[6]提出了一种基于运动规划与自适应的吊车欠驱动系统控制律，在系统参数未知条件下仍能实现系统良好的控制性能。文献[7]提出了反馈线性化的无模型自适应控制器和模糊逼近的自适应滑膜控制器对欠驱动吊车系统进行控制的方法。文献[8-9]采用基于能量最优解和准PID 的吊车欠驱动控制策略。文献[10]采用一种双吊车协同运行控制器，并利用Lyapunov 方法和LaSalle 不变性原理证明了系统趋于平衡点的稳定性。

本文在建立欠驱动门式起重机动力学模型的基础上，通过仿真实验验证能量耦合控制律对门式起重机欠驱动系统的控制性能。本文设计的仿真实验模型可向学生全面地展示门式起重机的完整控制过程，有助于进行欠驱动系统非线性控制方法的理论研究和实验教学工作。

1 门式起重机动力学模型

门式起重机受力示意图如图1 所示。

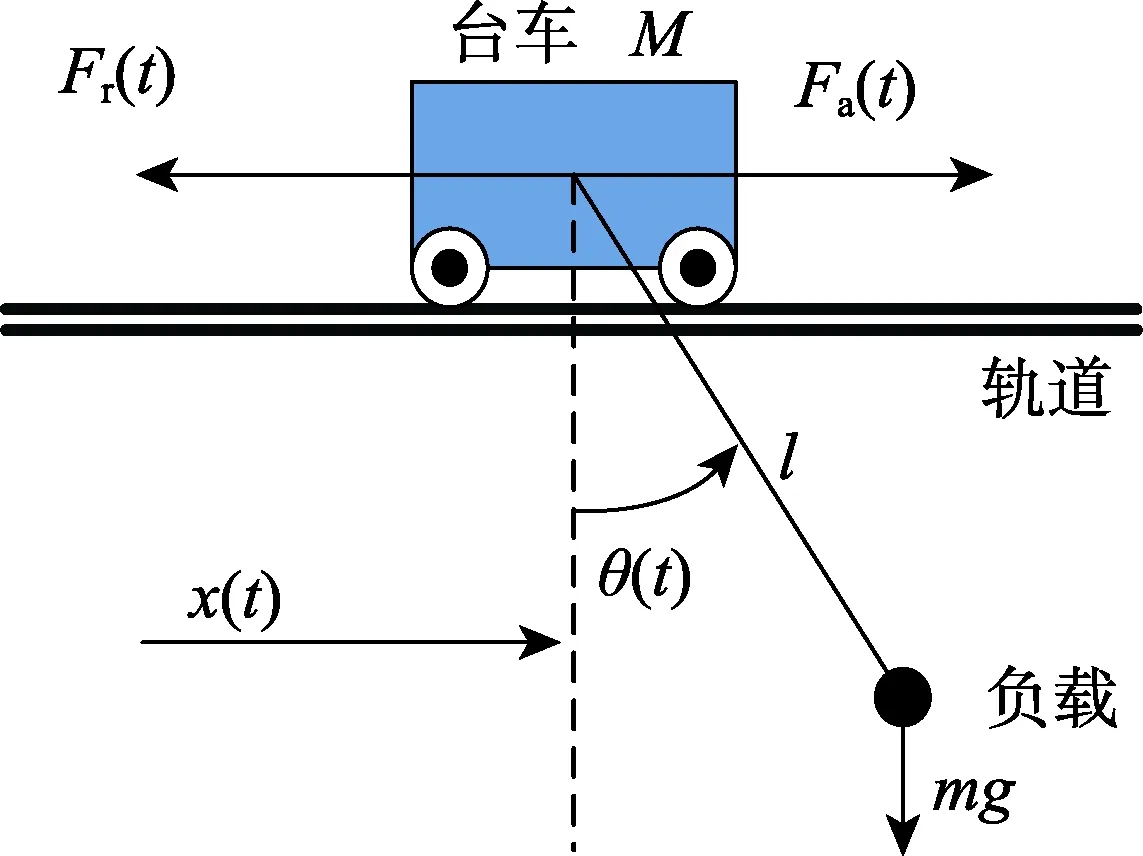
图1 门式起重机受力示意图

利用Euler-Lagrange 方程建立门式起重机动力学模型[11]，

式中，M 表示台车质量；q 表示门式起重机系统的状态向量； M ( q )表示系统的惯量矩阵；Vm( q ,)表示系统的向心-柯氏力矩阵； G ( q )表示系统的重力势能向量；U 表示系统的的控制向量。以上参数的分别定义如下：

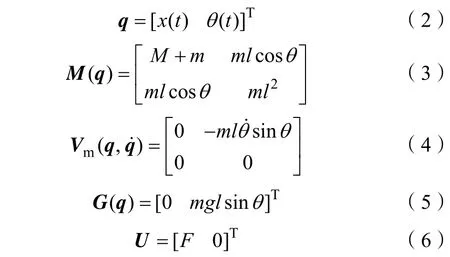
式中，m 表示负载质量；l 表示吊绳绳长；g 表示重力加速度；F 为水平方向作用于台车的合力由且

其中Fa表示电机作用于台车的驱动力，Fr表示台车与轨道之间的摩擦力，

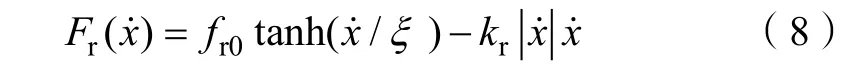
其中 fr0, ξ,kr∈R 是与摩擦力有关的参数。

2 能量耦合控制律

由门式起重机的机械能构造能量函数[12]：

为了增强台车位移x(t)与负载摆角θ(t)的动态耦合关系，使台车能准确运行至目标位移x(t)，并且有效抑制负载摆角θ(t)，构造如下所示基于能量函数的正定标量函数：

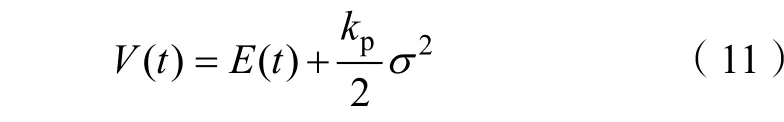
式中， kp∈R+为正的控制增益，σ 为负载在X 方向定位误差，满足

式中，e 表示台车在x 方向相对于终点目标位移xub的定位差值，定义为：

对 V (t ) 关于时间求导，代入式（1），可得

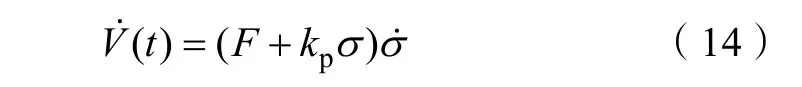
基于 V˙ (t ) 所示形式，采用Lyapunov 方法设计如下所示基于能量耦合的控制律：

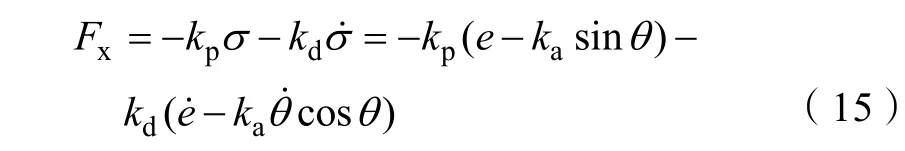
式中， kd∈R+为正的控制增益。

3 仿真实验

3.1 仿真系统搭建

Matlab/Simulink 仿真软件具有强大的数学解算和绘图能力[13]。本文应用Matlab/Simulink 中的function、积分器、选择器、示波器等模块设计了如图2 所示的仿真系统。门式起重机实验模型系统参数如表1 所示，各主要控制量的增益设置如表2 所示。

图2 门式起重机控制仿真系统

表1 门式起重机实验模型系统参数

表2 各主要控制量的增益

实验仿真系统可通过扰动开关选择是否有扰动信号接入，实验结果可通过输出示波器直观的显示台车位移x(t)、负载摆角θ(t)、控制力F(t)的输出曲线，实验数据将通过To Workspace 模块保存至工作空间，便于量化分析实验结果。

3.2 各主要模块的程序代码

（1）动力学模型模块内代码为：

function ddq = fcn(q,dq,f)

q1=q(1); q2=q(2); dq1=dq(1); dq2=dq(2);

M=12; m=1; l=1; g=9.8; %系统参数

q2=mod(q2,2*pi);

d11=M+m;

d12=m*l*cos(q2);

d21=d12;

d22=m*l*l;

c12=-m*l*sin(q2)*dq2;

g21=m*l*sin(q2)*g;

D=[d11,d12;d21,d22]; %(式3)

C=[0,c12;0,0]; %式(4)

G=[0;g21]; %式(5)

ddq=D([f;0]-C*[dq1;dq2]-G); %式(1)

（2）能量耦合控制律模块内代码为：

function f = fcn(q,dq)

q1=q(1); q2=q(2); dq1=dq(1); dq2=dq(2);

kp=8.5; kd=42; ka=1; pdx=3; %控制律参数设置

e=q1-pdx; %式(13)

f=-kp*(e-ka*sin(q2))-kd*(dq1-ka*dq2*cos(q2)); %

式(15)

（3）摩擦函数模块内代码为：

function fr = fcn(ddx)

fr0=4.4; kw=0.1; kr=-0.5; %摩擦力相关参数

fr=fr0*tanh(ddx/kw)-kr*abs(ddx)*ddx; %式(8)

（4）扰动函数模块内代码为：

function f = fcn(t)

f=0;

if t>18&&t<19

f=2.5*sin(6*pi*(t-18)); %正弦扰动

elseif t>28&&t<29

f=2; %脉冲扰动

else f=0;

end

3.3 准确性实验

切换扰动开关，关闭扰动函数，然后进行门式起重机控制仿真系统实验，以验证能量耦合控制律对欠驱动门式起重机控制的准确性。

实验结果如图3 所示。根据式（15）能量耦合控制律，台车运行约15 s 后，准确且无超调地运行到目标处，位移xub＝3 m，整个过程中负载摆角 θ∈[ -4 .6°,2.4°] ，并且在台车到达目标位置时迅速向零收敛，很好地抑制了负载的残余摆动，表明控制律对台车定位差值与负载摆角抑制准确性较高。

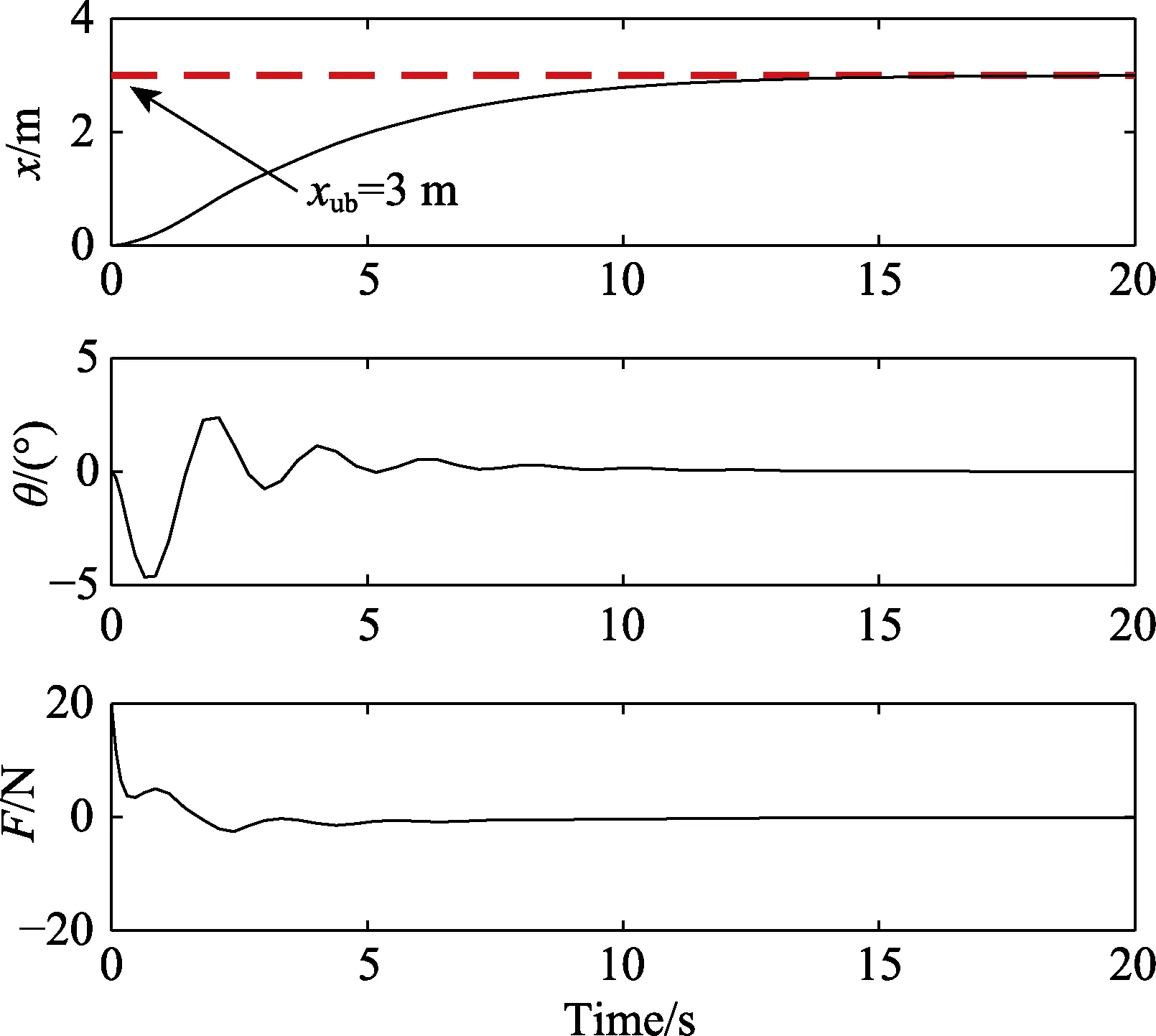
图3 台车控制运行结果

图4 抗干扰运行结果

3.3 鲁棒性实验

鲁棒性是检验控制律设计的另一重要指标。在仿真实验中，通过添加正弦扰动和脉冲扰动，模拟门式起重机运行过程中可能遇到的风载、撞击等外部扰动，可以检验能量耦合控制律对控制系统的鲁棒性。切换扰动开关，打开扰动函数，进行仿真试验，在18～19 s添加正弦扰动，在28～29 s 添加脉冲扰动。

仿真实验表明：系统使台车准确、稳定地运行到目标位置。图4 所示为仿真实验结果。当突遇外界扰动后，系统约在7 s 后负载运行位移再次回归至目标位移处，负载摆角向零收敛，并有效抑制了负载的残余摆动，整个过程中负载摆角 θ ∈[ -2 .0°, 1.8°] ，台车定位差值 e∈[ -0 .15 m,0.03 m]，满足系统的鲁棒性要求。

4 结论

本文应用Matlab/Simulink 软件设计的欠驱动门式起重机的非线性控制方法仿真实验系统，实验结果说明：采用欠驱动能量耦合控制律的控制过程，可以使台车在运行约15 s 后准确到达目标位置，而该过程中负载摆角 θ ∈[ -4 .6°, 2.4°] , 能够满足控制准确性的要求。当系统遇到外界扰动时，约7 s 内能够消除干扰，使台车位移与负载摆角恢复稳定，鲁棒性较强。利用该仿真实验系统，既可以进行欠驱动门式起重机非线性控制方法的理论研究，也可以用于欠驱动控制相关课程的实验教学，具有广泛的应用价值。