基于矩阵束的换流变压器对称性励磁涌流识别方法

南天琦，朱希松，张玉浩，韩 波，刘世明

（1.电网智能化调度与控制教育部重点实验室（山东大学），山东 济南 250061；2.国网山东省电力公司济南供电公司，山东 济南 250012；3.国网浙江省电力有限公司杭州供电公司，浙江 杭州 310016）

0 引言

特高压直流输电在我国得到了广泛的应用。在特高压直流输电中，换流变压器作为换流站的主要设备，其可靠运行关系到特高压直流输电的安全性和稳定性。然而，对称的励磁涌流常使差动保护失灵。例如，2007 年1 月28 日，天广直流输电系统换流变压器差动保护故障；2008 年12 月30 日，荆门站特高压直流输电系统换流变压器差动保护故障；2009 年12 月3 日，云广直流项目楚雄站换流变压器差动保护故障［1］。

在特高压换流站上有两个极，每个极上有整流器和逆变器，还有两个换流变压器并联，联接方式为Y／Y，Y／△。特高压换流变压器整定差动保护包括大差保护和小差保护。大差保护的保护范围包括从换流变压器网络侧的交流开关到换流变压器阀侧的所有线路元件，TA1、TA2、TA4、TA6 构成了大差保护。采用小差保护的保护范围为相应的换流变压器。TA3和TA4 构成换流变压器T1 的小差保护，TA5 和TA6构成换流变压器T2 的小差保护［2］。如图1 所示。

图1 特高压换流变压器大差保护和小差保护

2 大差保护对称性励磁涌流分析

2.1 大差保护仿真模型

借助PSCAD 软件平台，根据实际参数建立±800 kV特高压直流输电工程的仿真模型，如图2 所示，包括交流侧等效电源、特高压换流站 （整流侧和逆变侧）、±800 kV 两极直流输电线路、等效负荷以及无功补偿、各滤波器和控制环节。该工程输送功率为5 000 MW，直流输电线路电流为3.125 kA。换流站内每极对应有两组换流变压器运行，即高端一组Y／△和Y／Y 换流变压器、低端一组Y／△和Y／Y 换流变压器。每组中Y／△和Y／Y 换流变压器额定容量为732.3 MVA，额定电压分别为

图2 特高压换流变压器仿真图

对称性励磁涌流是指某换流变压器空载合闸产生励磁涌流，另一换流变压器产生相应的和应涌流。由于大差保护的差动电流是两个换流变压器的差动电流与小差保护的差动电流之和，因此大差保护的差动电流是对称的。大差保护中的对称差动电流称为对称性励磁涌流。

2.2 对称性励磁涌流原因的理论分析

在同一母线上并联两个变压器，一个空载合闸，将使与之并联的变压器铁芯饱和，并产生和应涌流。并联换流变压器的等效电路如图3 所示［5］。

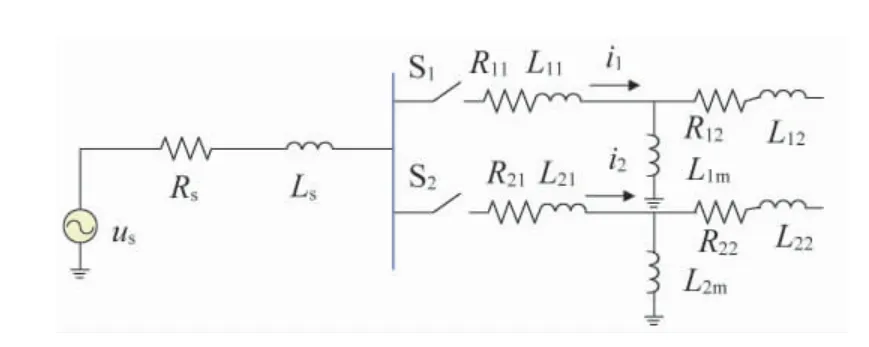
图3 并联换流变压器等效电路

图3 中，us、Rs、Ls为系统电压、电阻和电感，S1、R11、L11、L1m、R12、L12分别为T1的开关和等效变压器参数，S2、R21、L21、L2m、R22、L22为T2 的开关和等效变压器参数，T1 为空载闭合变压器，T2 为运行变压器。T1、T2 的磁量满足式（1）—式（2）。

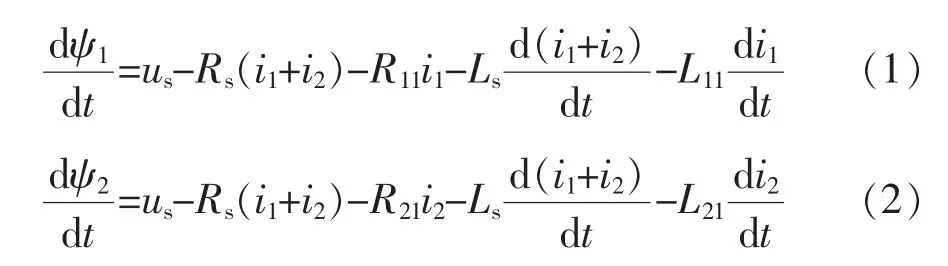
由式（1）和式（2）可以看出，磁链有相同的减小趋势。Δψ1、Δψ2偏磁逐渐累积，T2 铁芯达到负饱和点，产生和应涌流。偏磁逐渐累积，T1 的励磁涌流持续衰减。因此，励磁涌流与和应涌流方向相反，如图4 所示。

此时，该组换流变压器的大差保护波形及二次谐波含量如图5 所示。

图4 T1 和T2 小差电流

图5 对称性励磁涌流波形与对称性励磁涌流二次谐波比

可以看出，空载合闸0.4 s 后，大差保护的差动电流波形是对称的，且差动电流的二次谐波比低于二次谐波闭锁的阈值，因此差动保护不会闭锁。差动保护可能发生故障。从图5 中可以看出空载合闸时间为0.4 s，对称性励磁涌流接近额定电流IN的2 倍，在合闸后产生。在励磁涌流发生20 ms 后判定差动保护。由于对称性励磁涌流超过阈值（一般为0.4IN～0.7IN），差动保护必须按非励磁涌流判据进行动作。

2.3 传统励磁涌流判据的验证

二次谐波制动判据：对称性励磁涌流中二次谐波与基波的比值曲线如图5 所示。可以看出，合闸后20 ms（图5 中0.42 s），比例低于10%，表明二次谐波的含量在对称性励磁涌流很低，因此，二次谐波制动判据不能闭锁 （一般二次谐波谐闭锁门槛值是15%～20%，图5 中的门槛值是20%）。

间断角制动判据：分析图中对称性励磁涌流波形，计算出断续角仅为36°，一般间断角判据设定值≥40°，故间断角制动判据无法闭锁大差保护。

波形对称判据：从波形可以看出，各20 ms 大差周期的励磁涌流在10 ms 时间轴上是对称的，各上下半周期在5 ms 时间轴上也是基本对称的。因此，基于波形对称原理的励磁涌流识别也难以有效闭锁大差保护。

可以看出，仅从差动电流波形的特征来看，很难有效识别对称性励磁涌流。

2.4 对称性励磁涌流特性

电压与磁通的关系为：

式中：UM为电压最大值；ω为角速度；φ0为合闸角；φ为磁通；φ0为初始磁通；τ 为衰减时间常数。

由于磁通与电流的关系是非线性的，所以利用傅里叶对电流关系展开如下：

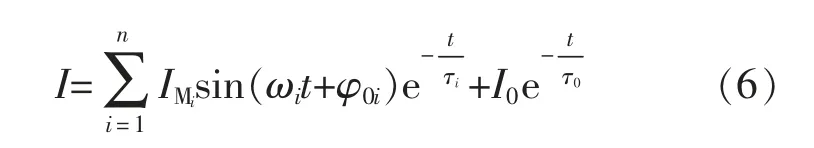
式中：IMi为i次谐波分量最大值；φ0i为i 次谐波分量合闸角；ωi、τi分别为i 次谐波分量的角速度与衰减时间常数；I0为直流电流值；τ0为直流电流衰减时间常数；n 为电流谐波分量个数。

在大差保护中，对称性励磁涌流为励磁涌流与和应涌流之和。由以上分析可知，对称性励磁涌流的电流中既有稳态分量，也有衰减分量。可以发现，无论是励磁涌流、故障电流还是对称性励磁涌流，都包含稳态分量和衰减分量。如果能提取出衰减因子，则可以准确地识别出这3 种电流。因此，引入矩阵束来提取电流的衰减系数。

3 基于矩阵束的对称性励磁涌流识别方法

3.1 矩阵束算法

矩阵束法是一种能够快速、方便地估计信号参数的信号处理方法。目前，矩阵束还应用于电力系统，如电力系统振荡识别、相量测量、工频分量提取等。由于矩阵束可以得到信号的幅值和衰减时间常数，因此选择矩阵束作为分析对称性励磁涌流的工具［6-8］。

研究的230 kV／36 kV、200 MVA 的三相变压器空载合闸在t＝1.004 s 时产生励磁涌流，取前8 个周期的波形。从1.004 s 开始，每个周期选取涌流数据用矩阵束方法计算，连续计算8 个周期，得到不同时刻的状态空间矩阵A并计算系统矩阵A主要的奇异值，如图6 所示。

由图6 可以看出，从变压器励磁涌流早期（t=1.004 s）到励磁涌流中期和后期，描述变压器的系统矩阵A 的主要奇异值在不同阶段发生变化。下面系统矩阵的奇异值具有一定的时变特性，因此采用矩阵束方法研究对称性励磁涌流是可行的。

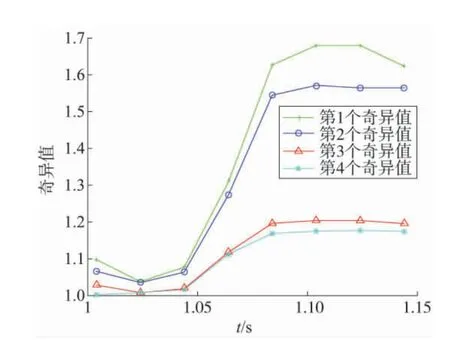
图6 系统矩阵A 的奇异值

矩阵束算法认为信号

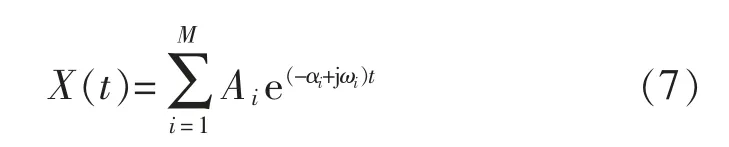
式中：Ai为信号i 的幅值；αi、ωi为信号i 的衰减系数和振荡频率。为了提取衰减因子，首先构造Hankel 矩阵为

式中：N 为采样点数；L 为矩阵束设置的束参数。

然后，利用采样序列1～N，2～N+1 矩阵Y1、Y2，并构造矩阵束Y2-λY1，其中λ 为阻尼因子。

求解两个矩阵乘积G 的特征值，G 为

由式（10）求对应模态的阻尼因子和振荡频率。

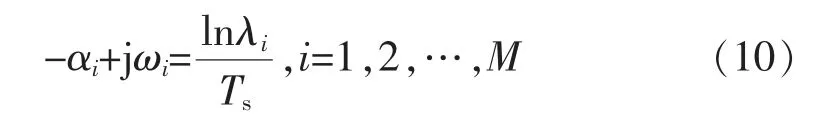
式中：Ts为振荡周期。

3.2 基于矩阵束的对称性励磁涌流识别

用矩阵束求出衰减因子后，通过（α＝t／τ）求出衰减时间常数，得到基波和二次谐波的衰减时间常数［9-11］，如表1 所示。

表1 四种电流的基本和二次谐波的衰减时间常数

由表1 可以看出，故障电流的基波电流衰减非常缓慢，其他3 种电流可以通过基波时间衰减常数来区分；对称性励磁涌流的二次谐波衰减较快，可由其余3 种类型的二次谐波衰减时间常数来区分；当励磁涌流与和应涌流衰减趋势基本一致时，基波衰减时间常数小于二次谐波衰减时间常数。

综上，判断故障电流的判据为

根据研究，τset设为10，在判断对称性励磁涌流与励磁涌流时，只要根据τ1与τ2的关系，当τ1>τ2时为对称性励磁涌流，τ1<τ2时为励磁涌流。

4 结语

讨论特高压直流输电系统中对称性励磁涌流产生的原因，并通过实际工况的仿真模型对对称性励磁涌流进行了仿真。可见，对称性励磁涌流确实会造成大差保护误动。基于这种情况，提出了一种基于矩阵束算法的特高压换流变压器对称性励磁涌流识别方法，并通过仿真试验结果验证了该方法的有效性。