基于混沌粒子群算法的变压器经济运行方式的研究
2020-09-29高佳程王毓玉梁少栋
高佳程,张 鑫,王毓玉,赵 健,梁少栋
(国网天津市电力公司城西供电分公司,天津 300100)
0 引言
变压器经济运行是在保证变压器安全运行和满足用户用电的基础上,通过选取变压器的最佳运行方式、优化调整负荷分配以及改善变压器运行条件等技术措施,来增强变压器输送能力,降低变压器电能损耗[1]。变压器经济运行方面的研究在我国开展较早,并取得了很多成果。仅以有功损耗最小为目标函数的临界点法来选择变压器的运行方式,虽然实现了损耗最小的目的,但变压器投切变换过于频繁,对电力系统的稳定性极其不利。传统的变压器经济运行方式的选择策略多以减小变压器有功损耗为目的,以变压器设备动作次数最少为约束,如时段控制法[2],多时段控制法[3],临界区间控制法[4]等。传统控制策略极少考虑到变压器运行中由于负荷越限造成的自身绝缘老化,进而影响到变压器的经济寿命[5]。文献[6]在文献[3]的基础上考虑了绕组热点温度,但增加了变压器的有功损耗,并未达到较好的降损效果。文献[7]以负荷预测为基础,利用遗传算法求解最优的变压器经济运行方式,但日负荷曲线峰谷差大,仅以日平均负荷为最小单位作为投切点来选择运行方式,忽略了一天中可能发生的负荷越限等问题。文献[8]利用禁忌搜索法,分时段求解出各时段内的最优运行方式,但变压器投切次数固定条件下时间段的划分问题并没有得到很好解决。
粒子群优化 (Particle Swarm Optimization,PSO)原理简洁,易于实现,无需梯度信息,且参数少,已在电网的扩展和检修计划、机组组合优化、负荷经济分配、最优潮流计算与无功优化控制、网络状态估计等领域得到应用[9]。
采用混沌粒子群算法 (Chaotic Particle Swarm Optimization,CPSO)寻求变压器经济运行方式,将松弛后的离散变量与连续变量交叉变异操作后进行优化,利用惩罚函数处理约束条件,有效解决了同一变电站内并列运行变压器的经济运行方式问题。最后对具体算例进行了计算,并与传统方法进行了比较,结果表明了该算法具有较好的求解能力。
2 变压器经济运行方式组合优化模型
2.1 变压器的综合功率损耗
变压器损耗包括空载损耗和负载损耗。变压器的综合功率损耗是指变压器运行中的有功功率损耗和因其消耗无功功率使电网增加的有功功率损耗之和[10],其表达式为

式中:Poz为空载综合损耗,Pkz为负载综合损耗;S 为变压器负载容量;SN为变压器额定容量;Qo和Qk分别为变压器空载无功损耗和短路无功损耗,且有Qo=0.01Io和Qk=0.01Uk,Io为空载电流,常用百分比表示,Uk为短路阻抗,常用百分比表示;Po和Pk分别为变压器空载有功损耗和短路有功损耗;K 为无功经济当量,单位为kW/kvar。
2.2 目标函数
经济运行的目的即为降低损耗,在构造目标函数时须着重考虑在不同时段内,并列运行的变压器在不同运行方式所产生的综合功率损耗。因此,要解决变压器经济运行方式问题即要划分出变压器不同的运行时段并确定各时段内的运行方式。设在规定时间段内变压器运行方式允许的最大改变次数为h,则在h+1 个时间段对应存在h+1 种不同的运行方式[11]。第t 个时间段的时间跨度为T(t),则待优化的目标函数即为h+1 个时间段内电能损耗总和最小,目标函数为

式中:ΔPt为第t 个时间段内的有功损耗,其计算公式为
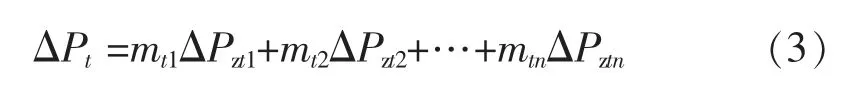
式中:n 为并联变压器台数;ΔPztj为第t 时间段内第j台变压器的综合有功功率损耗;mtj为变压器的运行系数,mtj取值为0、1 的整数变量。
mtj可表示为

2.3 约束条件
1)系统负荷平衡约束。
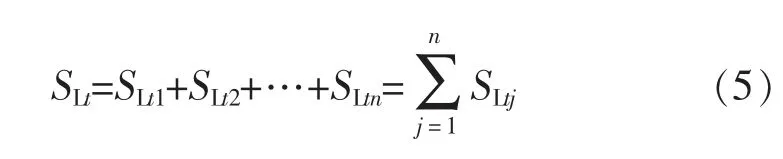
式中:SLt为第t 时间段内的负荷值;SLtj为第t 时间段内第j 台变压器的负荷值,且有SLtj=DtjSLt;Dtj为第t时间段内第j 台变压器的负荷分配系数,且有

绕组接线形式及变比均相同的多台变压器并联运行时,负载在各台变压器间的分配主要取决于变压器的短路阻抗。变压器的负载分配系数与自身短路阻抗成反比,与其容量成正比。此外,变压器的运行系数同样决定着负载分配系数的取值。由此可得,当n 台短路阻抗不同的变压器并列运行,其第j 台负载分配系数的计算式为
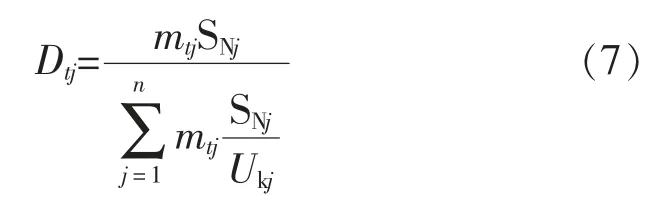
式中:SNj为变压器j 的额定容量;Ukj为变压器j 的短路阻抗。
2)变压器过负荷约束。

3)变压器绕组最热点温度约束。
变压器绝缘的热老化与绕组的热点温度密切相关。由阿伦尼乌斯定律可知,变压器的热老化速率可直接表达为[12]

式中:τmax为变压器绕组的最热点温度;A 为频率因子,当取参考温度为110 ℃时,A=9.8×10-18;B 为老化斜率,其值取决于变压器的使用寿命,当参考温度取110 ℃时,B=1 500。
相对老化加速因数为

GT/T 15164—1994 《油浸式电力变压器负载导则》规定,油浸式变压器绕组的热点温度基准值为98 ℃,在此温度下绝缘的相对老化率为1。在80~140 ℃范围内,温度每增加6 K,老化率增加1 倍。
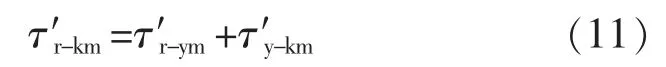
变压器的相对老化率计算方法为
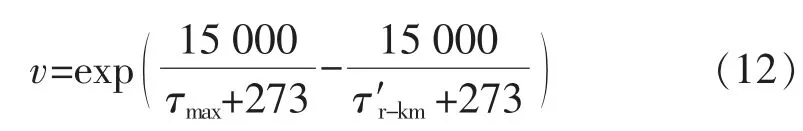
综上,变压器绕组的最热点温度需满足
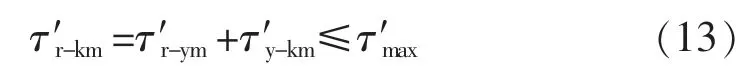
3 混沌粒子群优化算法
3.1 混沌粒子群优化算法的基本原理
粒子群算法的思想源自鸟群捕食。鸟群在某一区域内随机搜索食物,当鸟群中的所有个体都明确自身位置与食物位置的距离时,捕食搜索最简单有效的策略即为搜索目前距离食物最近的鸟的周围区域。粒子群算法即是以此为模型衍生出的智能优化算法[13]。算法的基本原理可以描述如下。
一个由w 个粒子构成的种群(即粒子群的种群规模为w)在D 维搜索空间内以某一速率飞行。搜索过程中的每个粒子考虑到自身搜索过的历史最优解及种群中其他个体的历史最优解,在此基础上进行位置(状态,也就是解)的变化。
第i 个粒子的位置表示为xi=(xi1,xi2,...,xiD);第i个粒子的速度表示为vi=(vi1,vi2,...,viD);第i 个粒子经历过的历史最好点表示为pi=(pi1,pi2,...,piD);其中i=1,2,…,w。
群体内(或邻域内)所有粒子所经历过的最好的点表示为:pg=(pg1,pg2,...,pgD),其中1≤g≤w。
设迭代次数为K,在第k 次迭代过程中,粒子的位置和速度根据式(14)和式(15)进行变化。

式中:d=1,2,…,D;c1、c2为学习因子,一般为0~2 之间的正常数,学习因子使粒子具有自我总结和向群体中优秀个体学习的能力,从而使个体能够在搜索过程中逐步收敛于自身的历史最优解及群体 (或邻域)的历史最优解;ξ、η 均为[0,1]内均匀分布的伪随机数;ω 为惯性权重,其值表征了粒子对当前搜索速度的继承程度为第i 个粒子在第k 次迭代中d维速度为第i 个粒子前k 次迭代中d 维最优位置为第i 个粒子在第k 次迭代中d 维位置为所有粒子在前k 次迭代中d 维最优位置。
在上述粒子群优化算法中,粒子群的初始化和更新过程具有一定的随机性,使得pid、pgd的更新具有一定的盲目性,因此将影响迭代过程的收敛性,还容易陷入局部最优解。混沌运动具有遍历性,将混沌现象引入粒子群优化算法中可以有效避免算法陷入局部极值点,改善算法的收敛速度和精度。
混沌是由确定性方程得到的具有随机性的运动状态,其遍历特性使混沌变量能在一定范围内按自身“规律”不重复地遍历所有状态。CPSO 的基本思想是首先产生一组与优化变量相同数目的混沌变量,用类似载波的方式将混沌引入优化变量使其呈现混沌状态,同时把混沌运动的遍历范围放大到优化变量的取值范围,然后直接利用混沌变量搜索[14]。
利用Logistic 方程构造混沌系统

式中:μ为控制参数,取μ=4;设0≤s0≤1,则系统完全处于混沌状态,迭代出确定的序列s0,s1,s2,......
在每个粒子每次迭代求解后,根据混沌原理令其做混沌遍历运动,以使得整个粒子种群可以搜索全部解空间,而不会停留在局部最优的极值点上。然后再对每一个可行解计算其适应度值,得到性能最优解。
3.2 变压器投切状态变量及约束条件的处理
在算法迭代运行过程当中,将变压器投入与退出运行的状态对应的0、1 正数变量松弛为区间[0,1]内的连续变量[15],针对离散变量设定相应的阈值来确定变压器是隶属于运行状态1 还是停运状态0。其判定操作如下[16]:

式中:rand为[0,1]区间内均匀分布的伪随机数。
对式(5)、式(8)、式(13)中所述等式、不等式约束采用罚函数[17]的构建方法转化为无约束目标函数优化问题求解,目标函数为

式中:λ、φ、ζ 为惩罚因子,均为很大的正数;ε 为一极小正数。可根据约束条件的不同设置不同的违反约束条件程度的等级,在不同的等级中使用不同的惩罚因子,违反约束条件越严重,惩罚因子越大[18]。
3.3 算法中的交叉和变异过程
为了避免算法过早地陷入局部最优解,当完成迭代寻优操作后引入交叉、变异操作来解决问题。该过程主要包括2 个方面。
1)交叉操作。
经式(14)、式(15)、式(19)迭代完成后的个体,取其运行状态变量为mi=(mi1,mi2,...,miD),对于0、1取值的整数变量可视为二进制编码的D 维向量mi。最常用的交叉操作即在双亲染色体上选择合适的断点,再互相交换断点处的基因序列,重新构成新的子代染色体。其具体操作过程,如表1 所示。
每次粒子位置更新完成后,根据选定的交叉概率,从种群中选取相应数量的个体形成粒子池,池中的个体对应双亲染色体,两两随机交叉,形成相应数目的子代染色体,并用子代替双亲形成相等数量的子代粒子,完成粒子群完成进化的同时保证了种群规模的稳定[19]。

表1 当D=6 时,变压器状态变量交叉操作
对于松弛后的状态变量选择凸组合交叉操作,对于双亲
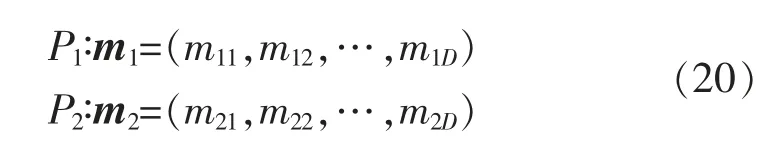
凸组合交叉是将上述2 个染色体进行如下操作[16]:

其中α>0,即
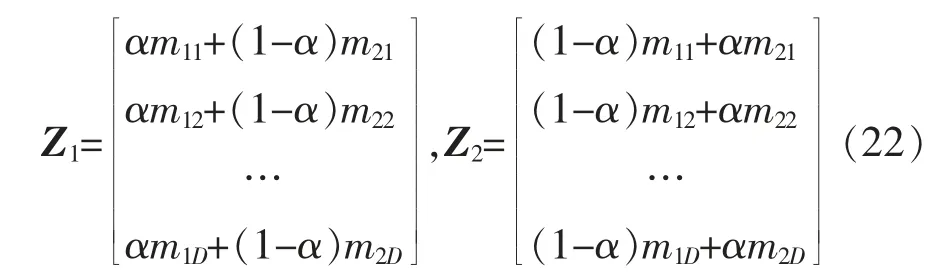
由此可得,当进行交叉操作后所得的新个体仍满足等式约束条件,即仍为可行解。但是,由于α>0,这样的交叉操作将导致基因取值向中间汇集,新种群得到的染色体所覆盖区域将越来越小,针对这一问题,由于粒子群的寻解过程将使群极值点和个体极值点收敛于最优点附近,因此,可以利用粒子群迭代一定次数后再进行凸组合的交叉操作。
2)变异操作。
对于运行参数变量对应的染色体m=(m1,m2,…,mD),位值变异是在其基因中任选2 位me和mf,进行如下变异。

式中:δ 为变异步长,可服从指数分布、正态分布或均匀分布等。
交叉和变异操作使得后代粒子继承了父母双方的特性,提高了对最优解的搜索能力,有效避免陷入局优。
利用粒子群算法求解并列变压器经济运行方式的算法流程如图1 所示。
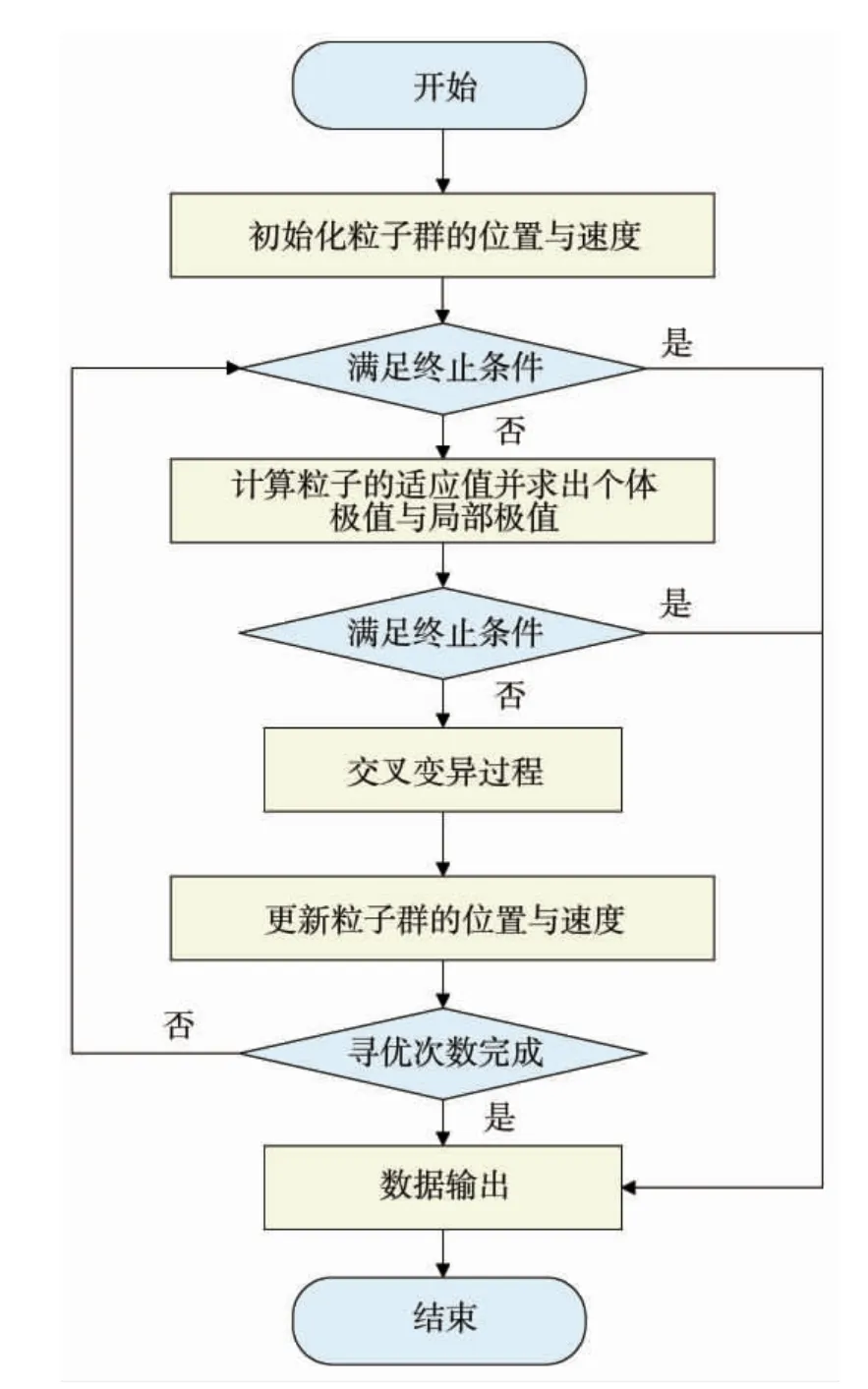
图1 粒子群算法求解并列变压器经济运行方式流程
4 算例分析
为了验证算法的有效性,以某110 kV 变电站为例,该变电站内有31.5 MVA 和50 MVA 两台变压器,其具体参数如表2 所示。该变电站一天内监测得到的日负荷预测值如表3 所示。
使用CPSO 算法进行寻优求解时,为达到较好的收敛性种群规模,设定种群规模为100,选用时变惯性权重[20],ω∈[0.4,1.2],求解过程中的第k 次迭代时,学习因子c1=c2=1.49[21]。交叉率取0.25,变异率取0.1。
以变压器一天内总能耗为目标函数,考虑式(5)、式(8)和式(13)的约束条件,利用CPSO 算法确定变压器运行方式如表4 所示,表5、表6 给出了寻优结果和传统方法与CPSO 算法的比较。从表中信息可得,当不采用控制策略而以临界点划分经济运行区间时,变压器投切次数过于频繁,甚至可能危及电力系统的安全运行;当采用时段控制法时投切次数减少但损耗明显增大,更重要的是,上述方法都不易求得较好的投切时间;采用临界区间法所得损耗相比CPSO 稍小,但运行中两台变压器需多1 次投切;利用CPSO 算法进行寻优求解时,变压器投切次数明显减少且总能耗相对较低。引入交叉变异操作后的CPSO 算法随迭代次数增加的收敛曲线如图2 所示。
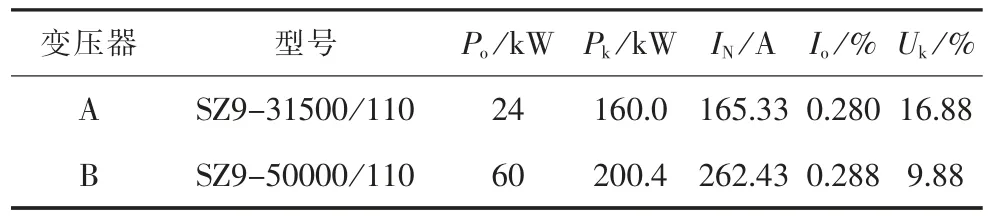
表2 变压器参数

表3 某日负荷预测结果
同时,根据寻优结果可以发现,在实际运行过程中可选择变压器A 作为主变压器,而变压器B 选作备用变压器。由此确定的运行方式从经济上达到了能耗最小,有效地实现了节能降损;从变压器安全运行角度上,避免了变压器的过载运行和绕组的热老化,保证了使用寿命。同时还减少了断路器等开关设备的动作次数,保证了电力系统的稳定运行。
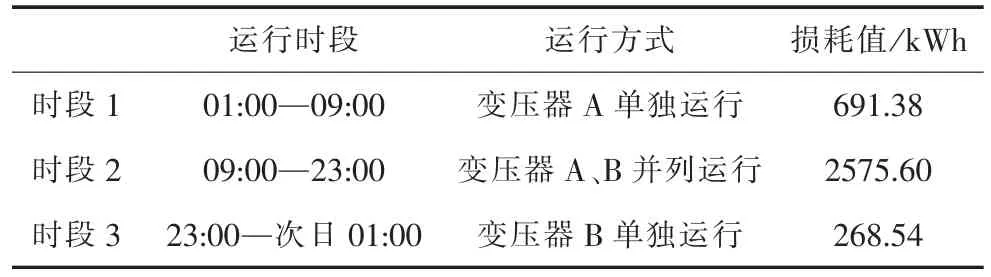
表4 CPSO 算法确定的运行方式

表5 几种控制策略各时刻运行方式

表6 几种控制策略的比较

图2 收敛曲线
5 结语
通过对混沌粒子群算法的改进,成功解决了并列运行的变压器的最优经济运行方式的选择问题。该种选择策略与传统方法以及利用其他优化算法寻优的选择策略相比,优势主要体现在:
1)既保证了单台变压器负荷不越限及绕组绝缘不受损,又达到了有功功率损耗最小的目的;
2)该种选择策略所用到的优化算法结构简单,易于实现;
3)利用算法求解过程中所引入的交叉和变异操作很好地避免了寻优结果陷入局部最优解。
算例结果也验证了该方法的有效性。
