线性三层规划问题的模糊求解算法
2020-09-28陶李曼长江大学信息与数学学院湖北荆州434023
陶李曼 (长江大学信息与数学学院,湖北 荆州 434023)
洪云飞 (长江大学期刊社,长江大学信息与数学学院,湖北 荆州 434023)
吕一兵 (长江大学信息与数学学院,湖北 荆州 434023)
多层规划是一种具有递阶结构的系统优化问题[1~4]。在多层规划中,每一层都有自己的目标函数、约束条件和决策变量;每一层之间具有相对的独立性,但是又会影响到其他决策层。一直以来,对多层规划的研究主要集中在二层规划问题。在二层规划中,上层决策者首先给出自己的决策;下层决策者以上层决策为参数,选择对自己最为有利的决策,然后再反馈给上层。在这样不断交互的过程中,双方最终得到“最优解”。
相比于双层情况,一些实际决策问题可能涉及3个不同的决策者,同时这些决策者分别处于不同的层面。例如,在供应链管理问题中,上层的材料供应商通过制订合适的材料价格来寻求利润的最大化;中层的制造商通过制订产品价格来最大化其利润;而下层的分销商通过订购合适数量的产品来最大化个人的利润。类似于双层规划,在上述三层决策问题中,每位决策者通过各自的决策变量来优化其目标函数,同时又会受到其他2位决策者的行为影响。
三层规划问题正逐步引起研究者的关注。Bard[5]以下层问题的最优性条件代替下层问题,同时将互补约束条件作为中层目标函数的罚项,得到了相应的二层规划问题;然后对得到的二层规划问题再次使用K-K-T条件转化方法,从而得到了单层近似问题;最后对于单层近似问题设计了基于相邻极点搜索的算法。在此基础上,White[6]提出了线性三层规划的罚函数方法,首先运用线性规划的对偶理论将线性三层规划问题转化成相应的二层规划问题;然后将二层规划问题采用文献[2]中的转化方法,从而得到单层近似问题;最后以对偶间隙为罚项设计相应的罚函数算法。Sinha[7,8]提出了线性多层规划问题的K-K-T条件转换方法。Ruan等[9]研究了多层规划相关问题,分别讨论了线性多层规划的最优条件和几何性质,在约束集S是有界且为非空的假设下,证明了线性多层规划的可行集不仅由约束集S的一些非空面的并集组成,而且是连通的。Faísca[10]将二层规划的参数求解算法推广到三层规划问题,其核心思想是将下层问题的最优解以上一层的决策变量进行。针对线性三层规划问题的最优解在可行域的顶点取得的性质,Zhang等[11]设计了一种K-次最好算法,并且给出了相应的算例。
相比于传统的数值优化方法,模糊规划方法可以将各层决策者的目标结合起来考虑,从而使优化后的各层决策者的目标值达到某种意义上的平衡。Lai[12]提出了最优性隶属度和决策力度的概念来解决多层规划和分散优化问题。在涉及到层次决策过程中,上层决策者(DM)首先在不考虑下层问题的情况下确定其每个可能目标值的最优值,从而得到上层DM最优性的隶属度函数,类似地为决策变量建立隶属函数;然后观察下层问题在给定约束下独立计算出的最优值,并建立下层DM的最优性和决策权的隶属函数。若得出的解不满足条件,则下层DM的决策与相应的最优性和决策权的隶属函数将提交给上层DM进行修改,同时还要考虑到各层决策者的总体利益,直至达到最佳的解决方案。Shih[13]使用公差隶属函数的概念,并对多目标优化设计了一种模糊方法:首先各层次的DM根据所有约束的集合独立求解问题;然后根据公差建立所有DM目标函数的隶属度函数,上层DM确定最小满意值,通过引入辅助变量将原问题转化为线性规划模型,并采用单纯形法求解模型。该方法依赖于隶属函数的变化而不是顶点枚举,并且不会生成更高阶的约束,因此,不会增加原始问题的复杂性,并且通常会在单次迭代中解决多层规划问题。Sinha[14,15]设计了模糊数学规划(FMP)方法来获得线性多层规划问题的解决方案,该方法使用线性隶属函数的FMP方法来最小化目标:首先通过独立计算得到每一层DM的最优解;然后决策过程从第1层开始,第1层DM将其最优值范围和决策向量提供给第2层DM,该步骤使用隶属函数通过模糊集理论建模;如果得到的解决方案满足条件,则第3层也包括在内;否则,将修改公差值和隶属函数,直到得到前2层问题满意的解决方案,再将前2层的决策变量的首选值和目标函数的最优值界限传递给第3层DM;之后重复该过程,直到最后一层DM包含在系统中。
下面,笔者主要通过结合K-K-T条件转换方法与模糊方法来求解线性三层规划问题。该方法的主要思路为:采用下层问题的最优性条件,将三层规划问题转化为下层含互补约束的二层规划问题;然后采用模糊优化方法求解得到的二层规划问题,从而得到三层规划问题的最优解。
1 线性三层规划问题的数学模型
考虑的线性三层规划问题表述为:
(1)
式中:ci1∈Rn;ci2∈Rm;ci3∈Rp;bi∈Rqi;Ai∈Rqi×n;Bi∈Rqi×m;Ci∈Rqi×p;i=1,2,3;x,y,z分别为上层、中层和下层问题的决策变量;x∈Rn,y∈Rm,z∈Rp;f1,f2,f3:Rn×Rm×Rp→R分别是上层、中层和下层问题的目标函数。
定义1线性三层规划问题的约束集:
S={(x,y,z)≥0:Aix+Biy+Ciz≤bi,i=1,2,3}
对固定的x≥0,中层问题决策集:
S(x)={(y,z)≥0:Aix+Biy+Ciz≤bi,i=2,3}
对固定的(x,y)≥0,下层问题决策集:
S(x,y)={z≥0:A3x+B3y+C3z≤b3}
下层问题最优决策集:
P(x,y)={z≥0:z∈arg min[f3(x,y,z):z∈S(x,y)]}
中层问题最优决策集:
P(x)={(y,z)≥0:(y,z)∈arg min[f2(x,y,z):(y,z)∈S(x),z∈P(x,y)]}
三层规划问题的诱导域:
IR={(x,y,z)≥0:(x,y,z)∈S,(y,z)∈P(x)}
三层规划问题的最优解集:
OS={(x,y,z)≥0:(x,y,z)∈arg min[f1(x,y,z):(x,y,z)∈IR]}
为了保证所考虑的问题(1)存在最优解,假设线性三层规划问题的诱导域IR为非空紧集。
在线性三层规划问题(1)中,如果下层问题满足一定的约束规格,那么对于给定的决策变量(x,y),下层问题的K-K-T最优性条件为:
(2)
u(b3-A3x-B3y-C3z3)=0
(3)
vz=0
(4)
A3x+B3y+C3z-b3≤0
(5)
u,v≥0
(6)
式中:L(x,y,z,u)=f3(x,y,z,u)+u(b3-A3x-B3y-C3z)+vz是下层问题的拉格朗日函数;zL(x,y,z,u)表示函数L(x,y,z,u)在z处的梯度;u,v是拉格朗日乘子。
定理1[16](y,z)∈P(x)的充分必要条件是存在向量u,使得(x,y,z,u)满足上述条件(2)~(6)。
基于定理1,通过K-K-T条件,可以将线性三层规划问题(1)转化为如下含有互补约束的二层规划问题(7):
(7)
定理2[16](x,y,z)是三层规划问题(1)的最优解,当且仅当(x,y,z,u)为二层规划问题(7)的最优解。
基于定理1和定理2,结合模糊规划方法来寻找三层规划问题(1)的一个满意解(x,y,z)。
2 二层规划问题的交互式模糊规划方法
基于文献[17]中的模糊优化方法,下面设计问题(7)的模糊求解算法。这里f1,f2分别表示上层DM和下层DM的目标函数,先由上层DM给出一个模糊目标和最小满意水平,并且评价由下层DM提出的解,然后参照上层给出的模糊目标及最小满意水平,求出下层问题的最优解。为了简单起见,可以通过采用线性隶属函数来表示每层DM的模糊目标的特征,与其相应的线性隶属函数可定义为:
(8)
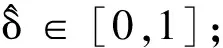
(9)
考虑到相应二层之间的整体满意平衡,则二层决策者的满意度可定义为:
根据耦合协调度模型测算出的结果,选取2005,2010与2015年淮海经济区旅游经济和城镇化的耦合度,并借助ArcGIS聚类工具对测度结果进行可视化(图1).
λ=min{μ1(f1(x)),μ2(f2(x))}
(10)
则问题(9)可变为:
(11)
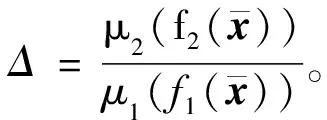
2.1 二层规划问题模糊算法交互过程的终止条件
一般而言,二层规划问题模糊算法的终止性条件一般采用如下2条:
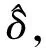
(2)满意度比Δ在给定的区间内,该上限由上层DM指定。
条件(1)表示上层DM为下层DM提出的解决方案所需的条件;条件(2)以便在2个级别之间保持整体令人满意的平衡。除非同时满足条件,否则上层DM需要更新其最小满意水平。
2.2 二层规划问题的模糊规划算法
二层规划问题的模糊规划算法具体步骤如下:
步2下层DM给出其模糊目标的隶属函数μ2(f2(x));
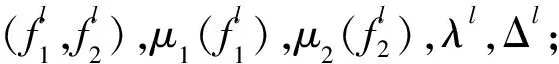
步4如果下层DM对上层DM提出的解满足最后的终止条件,那么上层DM就把这个解认为是满意解,从而算法停止;否则,进行下一步;
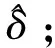
步6下层DM解问题(12)并向上层DM提出得到的解,返回步4:
(12)
3 数值试验
例1考虑如下线性三层规划问题,其中,x1∈R,x2∈R,x3∈R:
(13)
将上述三层规划问题通过下层问题的K-K-T条件转化为如下带互补约束的二层规划问题:
(14)
每层对应的目标函数最优解和最优值如表1所示。

表1 问题(14)每层对应的目标函数最优解和最优值
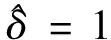
s.t. 2x2-x3≥2
众所周知,授人以鱼不如授人以渔,课堂教学更是如此。作为教师的我们不可能手把手地教学生读每一本课外书,因而阅读方法的指导就显得尤为重要。在阅读指导课上,我首先就对学生进行了阅读整本书的方法指导。
-3x1+x2-x3≥-12
-3x2-x3≥-24
x1≥2
-x3≥-6
-2+u1+u2+u3+u5-u6=0
u1(2x2-x3-2)=0
u2(-3x1+x2-x3+12)=0
u3(-3x2-x3+24)=0
u4(x1-2)=0
u5(-x3+6)=0
u6x3=0
λ∈[0,1],x≥0
f1=-9.6μ1(f1(x))=0.85
f2=2.15μ2(f2(x))=0.787
在文献[1]中,该问题的最优解为(4.667,1.0),其各层的最优值及满意度为:
f1=-16.668μ1(f1(x))=0.431
f2=-1μ2(f2(x))=0.25
f3=0μ3(f3(x))=0
由上述的分析可看出,模糊规划算法得出的解对应的各层满意度更高;文献[1]中给出的方法所得到的解虽然是例1的全局最优解,但对应的各层DM的满意度并不理想。
例2考虑如下线性三层规划问题,其中,x∈R,y∈R,z∈R:
(15)
将上述线性三层规划问题通过K-K-T条件转化为如下问题:
(16)
每层对应的目标函数最优解和最优值如表2所示:

表2 问题(16)每层对应的目标函数最优解和最优值
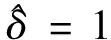
f1=-14.28μ1(f1(x))=0.7
f2=4.062μ2(f2(x))=0.618
在文献[14]中,该问题的最优解为(4,6,0),其各层的最优值及满意度为:
f1=-20μ1(f1(x))=0.916
f2=10μ2(f2(x))=0.025
f3=-8μ3(f3(x))=0.583
通过比较可以看出,模糊规划算法得出的解对应的各层满意度相对更高;而K次最好算法中上层DM完全占主导地位,下层DM无条件地服从上层的领导,并且在解线性多层规划问题相对应的模糊规划问题时,K次最好算法需要经过多次迭代才能得到问题的解。
4 结语
结合K-K-T条件转化方法与模糊方法求解了三层规划问题:首先通过K-K-T条件将三层问题转化为二层,再用模糊集理论中的隶属函数来描述各层决策者的目标函数,通过求解各层满意度的交互过程,最后达到整体的满意度平衡。由于最上层主观指定的满意度具有随意性,因此提出的方法需要进一步研究和完善。
