基于功率分辨算法的抗诱偏技术∗

（中国电子科技集团第十研究所 成都 610036）

1 引言

诱饵通常在目标受到导引头（PRS）跟踪时开始工作，以保护真实目标。有源诱饵辐射电磁波在导引头天线口面处形成复杂的电磁场以诱偏导引头，使导弹不能命中目标。目前国内外对抗诱饵诱偏干扰的研究主要集中单诱饵上，从目标雷达与诱饵信号功率差异、回波信号时延与回波多谱勒频移等方面进行抗干扰研究。对于时域、频域不完全重叠的干扰，可以采用信号分选、聚类分析等方法进行抑制；而对于时域、频域完全重叠的信号，目前的干扰抑制方法效果有限。文献［1～3］详细分析两点源诱偏下的弹载雷达性能分析。国内外抗诱饵诱偏干扰的方法主要有以下几种：1）脉冲前沿跟踪和时间选择技术［4］；2）边带跟踪和孤立脉冲的方法［5］；3）导弹飞行规律与聚类分析相结合的方法［6～7］；4）目标起伏检测法［8，9］。

在导引头天线口面处，诱饵发射信号与雷达信号形成的相位差直接决定了诱骗效果。当相差为π时，诱骗效果最好。但在ARM飞行过程中，要保持相位差恒为π是十分困难的，故一般认为相差为服从［0，2π］均匀分布［10］，本文正是利用此特性，分析了导引头的输出特性，并研究了基于功率分辨法的抗诱饵诱骗算法。在单诱饵诱骗下，算法能同时跟踪诱饵或目标雷达。在多诱饵诱骗下，算法能跟踪功率较大的目标雷达。

2 导引头输出特性

图1 诱偏时导弹与辐射源位置

为方便讨论且不失一般性。假定ARM、两辐射源以及导引头轴线在同一平面内，其相对位置关系如图1所示。图中O1、O2为两个辐射源位置、M为导引头位置、MT为导引头轴线方向、MT＇为导引头视线方向（导引头轴线与该方向重合时导引头输出角度为0，其中T＇称为视在目标，）。两辐射源与导引头轴线的张角分别为θ1、θ2（θ1>0，θ2>0 ，逆时针旋转为正），两源与导引头视线的张角分别为，辐射源O1与辐射源O2到导引头的张角为∆θ，导引头的输出角度为θ。从图中可以看出各角存在以下关系：

则到达PRS处的两辐射源的信号可以表示为

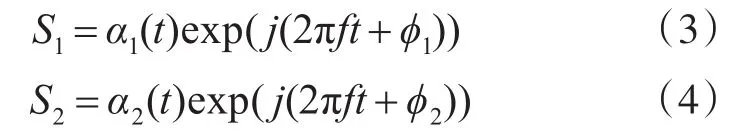
其中，a1(t)、a2(t)分别为两辐射源信号振幅，ϕ1、ϕ2分别为两辐射源信号到达PRS的初相。于是，干涉仪两阵元接收信号可分别表示为

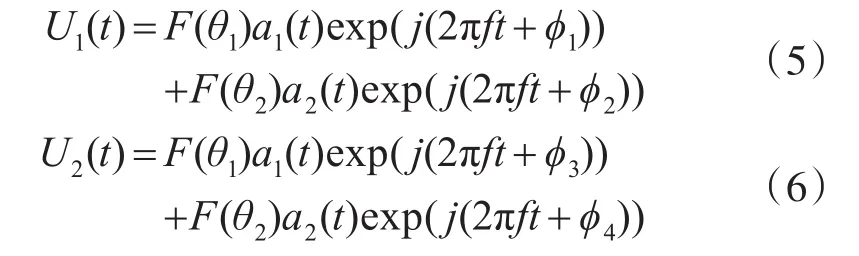
式中，F(θ)为天线阵元的方向图函数。在远场情况 下 ，可 认 为F(θ1)≈F(θ2) 。ϕ3-ϕ1=ksinθ1，ϕ4-ϕ2=ksinθ2，其中k=2πd/λ。

若两辐射源信号振幅恒定，令a2(t)=βa1(t)，∆ϕ=ϕ2-ϕ1，则U1、U2的相位差Φ可表示为

(3)浮选过程中添加的药剂具有一定的味道是烘干尾气有异味的内因之一，因此在浮选生产操作中尽量做到精确加量，一方面可减少药剂的浪费，另一方面可减轻烘干时尾气中的异味。

从式（13）可以看出，PRS输出角度是两辐射源信号的幅度比β、两辐射源到达角θ1、θ2以及两辐射源信号初始相位差∆ϕ的函数。

由于雷达常采用多个诱饵诱偏ARM，因此在多个辐射源诱偏环境下，导引头的视线方向由方程决定。于是，PRS的输出角度可以近似表示为

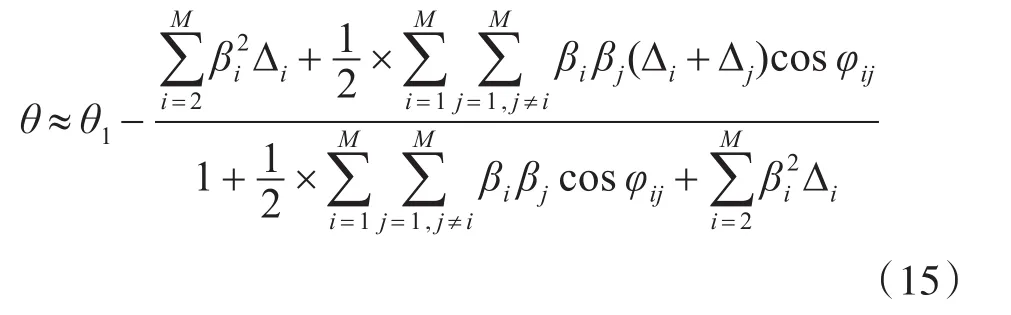
式中，βi=ai(t)/a1(t)，∆i=θi-θ1，φij=ϕi-ϕj，其中M、θi、ai(t)、ϕi分别表示辐射源的个数、角度位置、信号幅度、到达PRS的初始相位。

3 功率分辨法

根据式（13）所示，当β=1时，输出角度。导引头指向两辐射源的角度中心，与初始相位差∆ϕ无关。

当 ∆ϕ=π 时，输出角度θ=θ1-β∆θ/(β-1)。导引头指向两辐射源之外的某一位置，偏离程度与β的值相关。若在诱偏过程中，∆ϕ始终保持π，即相干两点源诱偏。

当β≠1且 ∆ϕ∈U[0，2π]时，PRS在一段时间内对输出角度进行统计平均，则有

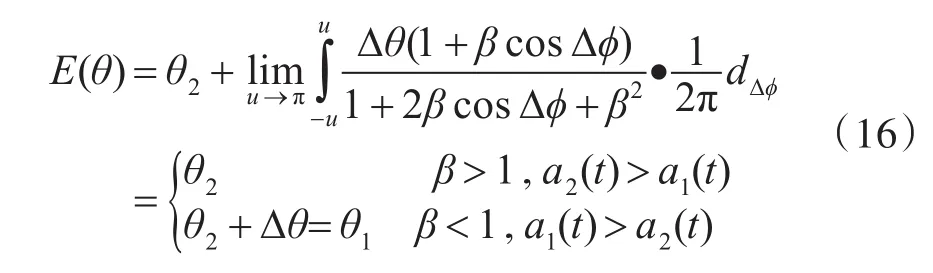
由式（16）可以看出，当β≠1时，通过数据积累后的统计平均处理，PRS指向功率较大的辐射源。因此，只要目标雷达信号的功率大于诱饵信号的功率（或幅度），输出角度经统计平均处理后，PRS最终会指向目标雷达。此时，目标雷达角度θr=E(θ)。

PRS的第一阵元天线接收到的相邻两脉冲重复周期内信号，其信号幅度可表示为

相邻两脉冲内，同一目标角度θ11、θ12几乎保持不变，可认为F(θ11)≈F(θ12)，则

在得到目标雷达角度θr的基础上，进而得到诱饵的角度qd=2qb-qr。

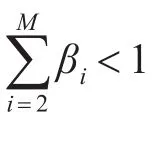
从式（23）可看出，算法输出角度指向目标雷达。但由于多个诱饵间的相互作用，已较难得到每个诱饵的角度信息。

4 仿真及结果分析

为验证算法性能，本文在蒙特卡洛次数150次，数据积累个数100个，θ1=0°，θ2=1°，k=2π的条件下进行了仿真实验。图2示出了算法抑制前后，导引头的输出角度值。虚线为未采用抑制算法的输出角度，实线为采用抑制算法后的输出角度。从图2中可看出，未采用抑制算法时，导引头输出角度为诱饵和目标雷达的功率中心。采用抑制算法后，当|β|>1.5dB时，PRS能跟踪目标雷达或诱饵。与功率重心所在角度相比，PRS跟踪大目标的性能得到明显改善。

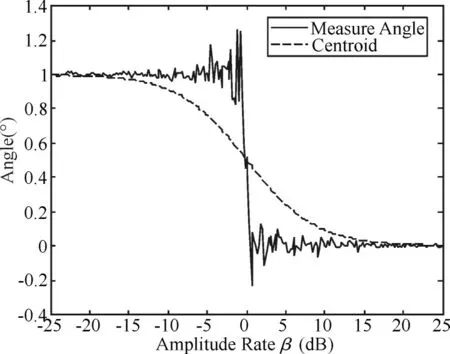
图2 输出角度曲线

图3示出了在不同β条件下目标雷达和诱饵的测量误差，实线为目标雷达角度误差，虚线为诱饵角度误差，诱饵的测量误差略大于目标的测量误差。

图3 目标雷达和诱饵测量角度误差曲线

图4示出了在多诱饵诱偏环境下目标雷达的测量角度误差。仿真中，k=4π，目标雷达角度0°，诱饵角度分别为1°，-1°，1.5°，2°。在多诱饵诱偏的情况下，只要SJR>0，使用功率分辨法即能跟踪上目标雷达。

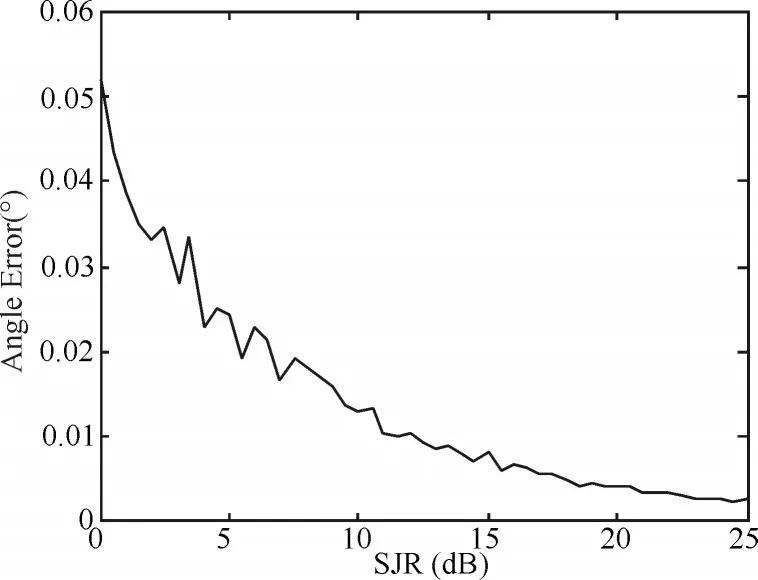
图4 目标雷达测量角度误差

在式（13）的基础上，推导出导引头输出角度的方差：

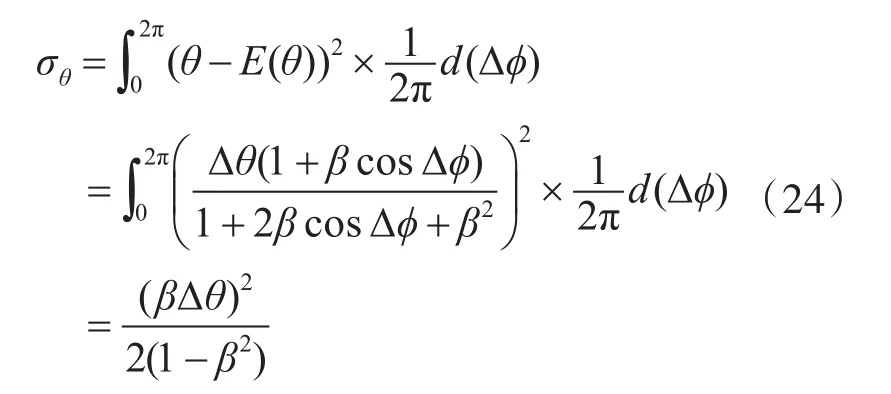
每次PRS的输出角度θ(i)相互独立，则数据积累N个后，经统计平均后得到均值角度的方差可表示为

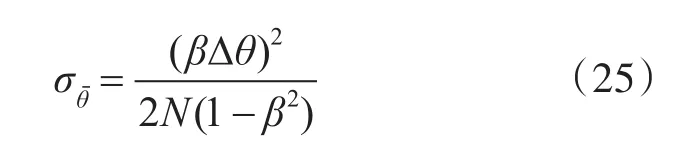
从式（25）可看出，输出均值角度方差与数据积累个数成反比，与两辐射源角度差的平方成正比，与两辐射源幅度比的平方成正比。图5示出不同β下测量角度的方差，仿真方差与理论方差几乎相同。

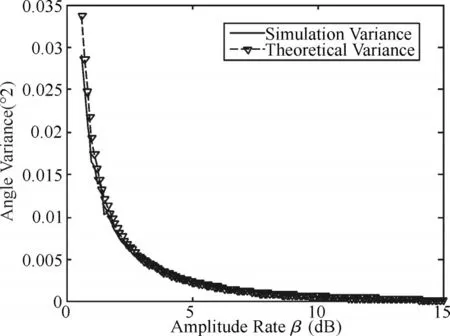
图5 测量角度方差曲线

图6示出数据积累数与测角误差曲线，可以看出在不同的幅度比β下，测角误差随着数据积累个数的增加呈现减小的趋势。当数据积累个数超过150次后，增加次数对减小测角误差性能的改善不大。

图6 测角误差与数据积累数曲线

5 结语

诱饵诱骗干扰对ARM带来了巨大了挑战。本文分析了在干扰环境下导引头的输出特性，并研究了一种易于工程实现的抗诱饵诱骗技术。采用此技术后，ARM可不受诱饵诱骗，而转向跟踪目标。本算法运算量低，仅需对导引头输出数据进行积累和简单数据处理，便能得到目标雷达和诱饵的角度信息，工程应用价值较高。