基于Bayes小子样理论的一维修正弹任务可靠度检验∗

（92941部队 葫芦岛 125001）

1 引言

一维弹道修正弹是采用阻力修正原理进行距离修正以提高纵向密集度的一种新型有控弹药，与传统无控弹药相比，具有高精度、高效费比的优点［1～3］。一维修正弹属于一次性使用的武器，任务可靠度直接武器装备作战效能的发挥，是试验鉴定必须重点考核评估的关键指标。但以频率稳定性为出发点的经典统计理论是以大子样为分析基础，而昂贵的武器系统若进行大量的试验是难以承受的。在只能进行少量试验的前提下，经典统计理论的有效性将大为降低。在这种情况下，Bayes小子样统计理论得到了广泛的重视和发展［4～8］。本文基于二项分布的Bayes检验，对一维修正弹的可靠性指标检验方法进行研究，为该型弹药的试验鉴定提供理论参考。

2 任务可靠度的指标要求

一维修正弹的任务可靠性可由任务可靠度指标来描述，即“在规定的条件下和规定的时间内，完成规定功能的概率”。一维修正弹使用阶段的典型任务剖面可分为发射前准备阶段，包括装弹、装订和供弹；发射无控阶段，包括发射、底排减阻、火箭增速和无控飞行；指令修正阶段，包括接收指令、阻尼机构动作和增阻修正；命中起爆阶段，包括命中、引信作用和起爆。

对一维修正弹的任务可靠度指标要求往往通过目标值p0和最低可接受值p1给出。目标值是装备在成熟期充分发挥固有可靠性潜力，经过可靠性增长后达到的，在设计研制阶段可靠性预计值必须达到并超过目标值。最低可接受值指合同或研制任务中规定的装备必须达到的合同指标，它是进行考核和验证的依据。

3 任务可靠度检验的数学描述

对于一维修正弹试验，我们关心的仅仅是这次试验中一维修正弹是否按照任务剖面规定的动作正常工作，即成功和失败这两种状态。这就是常说的成败型可靠性模型，可以用二项变量进行描述。事实上，设X是二项变量，它的取值为0或1，即

那么P{x=1}=p0就是成功的概率，即任务可靠度，而P{x=0}=1-p0=p1就是失败的概率。因此，关于二项变量分布参数的估计及检验就可以直接用于成败型可靠性模型参数的评估。设p0为使用方规定的任务可靠度的指标值，p1为使用方规定的任务可靠度的最低可接受值。于是，关于可靠性的检验就可以转化为不可靠性的检验。建立如下统计假设：

式中：λ为鉴别比，λ<1。

4 任务可靠度的Bayes综合检验方法

4.1 Bayes综合检验方案

假设检验是数理统计中一个重要的研究对象，从决策的观点来看，一个典型的决策问题是根据样本的取值情况，决定接受原假设还是拒绝原假设。在经典的统计假设检验中，考虑决策的出发点是犯两类错误的概率α和β，并由此确定决策的临界区域。而Bayes假设检验的出发点是考虑基于验前信息下的平均验后损失，决策的临界域着眼于损失函数。

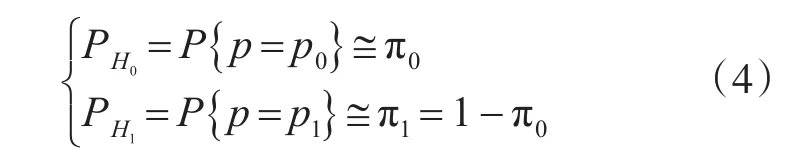
假定验前概率为

4.2 计算验前概率π0

利用贝叶斯公式，验前试验数为n0，成功数为s0，即验前样本为( )n0，s0，则验前概率PH0（或 π0）为

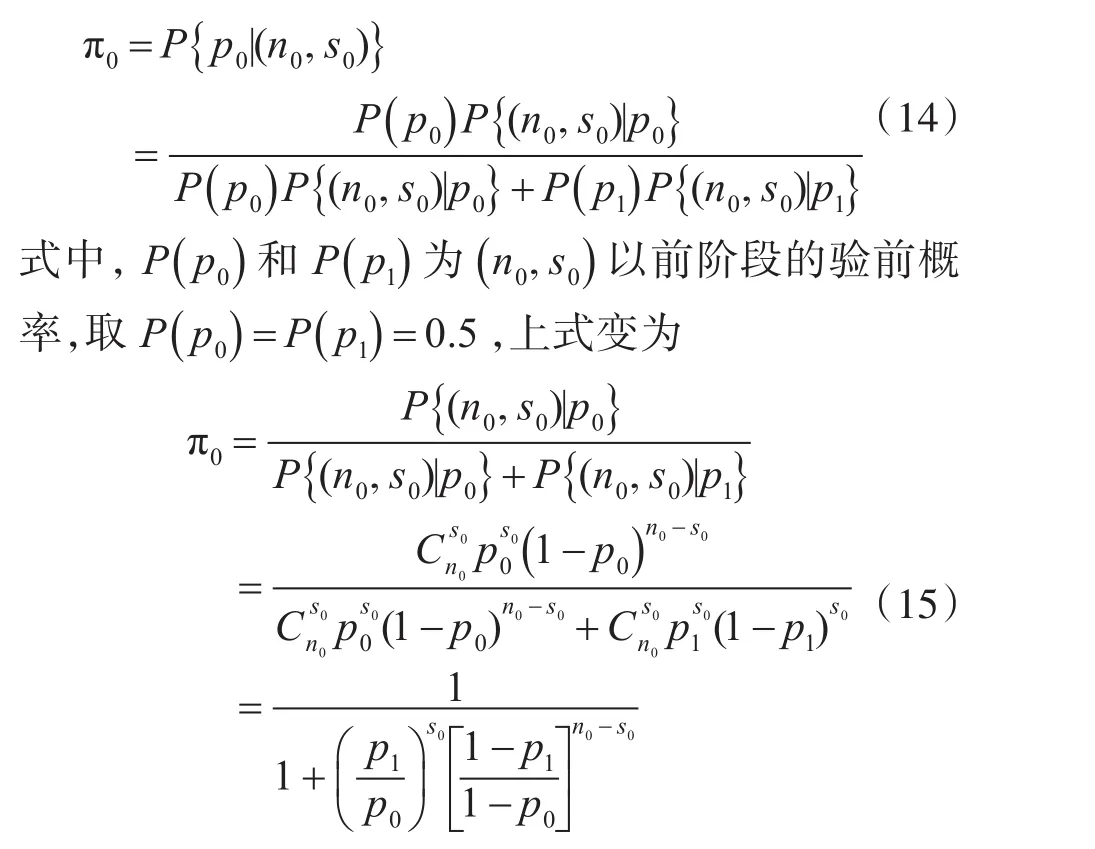
5 工程实例分析

本工程实例给出的指标要求和试验数据都经过处理，目的在于介绍一维修正弹可靠性评定方法的工程应用。取任务可靠度目标值p0=0.8，最低可接受值p1=0.75。若采用二项式经典假设检验方法，取双方风险为α=β=0.2，则所需试验次数为N=197。为减少试验消耗，采用Bayes综合检验进行一维修正弹可靠度检验。

假设正式试验前进行了n0=20次验前试验，成功数s0=16，即验前样本为（20，16）。由式（15）可得此时验前概率为

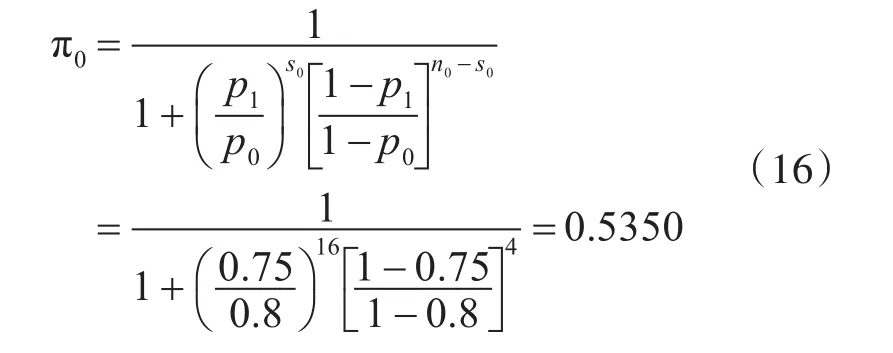
在验前概率为π0=0.5350条件下，利用式（4）～（13）可得如下贝叶斯检验方案及对应的双方风险，详见表1。

表1 贝叶斯检验方案（p0=0.8，p1=0.75，π0=0.5350）

6 结语

二项分布的贝叶斯假设检验方法利用了验前信息，因而较经典的假设检验方法有了很大改进，是小子样条件下实现装备关键指标考核的有效手段。本文针对以为修正弹任务可靠度考核试验时间长和消耗大的问题，提出基于Bayes综合检验的一维修正弹任务可靠度指标考核方法，通过数值算例给出了详细实施步骤。实例分析结果表明该方法能够有效减少试验样本量，降低试验成本，能够为该型信息化弹药的试验鉴定提供理论参考。